一种基于APES算法的弱ADS-B信号参数估计方法

李君惠，赵浩然，李武旭

(四川九洲空管科技有限责任公司，四川 绵阳 621000)

0 引 言

广播式自动相关监视(ADS-B)系统通过全球卫星导航系统(GNSS)等系统获得飞机的位置(经纬度、高度等)、速度、工作状态等信息，并把这些信息连同飞机的身份和类别信息按照固定的格式组成ADS-B信息帧，利用空-地、空-空数据链完成空中交通监视和航空器之间的信息传递。ADS-B系统是广播系统，不需要进行询问与应答，因而，相对于传统二次监视雷达，ADS-B简化了处理过程，可有效提高空管效率，并已成为一种应用极其广泛的空中交通管理技术。

虽然ADS-B系统具有建设成本低、监视范围广、精度高等诸多优势并且被各个国家广泛应用，但是由于建设成本和维护等原因，在偏远地区、沙漠、海洋等区域难以建设ADS-B地面站，因此难以实现上述区域的航空器监视覆盖。在这种情况下，星基ADS-B技术应运而生[1-3]，星基ADS-B系统将高灵敏度的ADS-B接收机安装在低轨道卫星上，通过卫星接收、解析航空器发送的广播信息，实时传输到地面站并补充到空管系统中[4]，由于卫星的覆盖面积广，因此提高了ADS-B的监视范围。实现星基ADS-B系统的关键技术之一是微弱信号处理，机载发射机系统并未针对星基ADS-B系统做出相应改进，进而导致卫星接收到的信号由于长距离传输功率很小。记l为损失功率，则有：

l=32.44+20lgD+20lgF

(1)

式中：D为信号传输距离；F表示信号频率，这里F=1 090 MHz。

经计算最大损耗可达160 dB以上，最小接收功率可达-105 dBm。在这种情况下信噪比极低，会严重影响ADS-B系统的信号处理与解码，从而降低系统性能，因此设计一套星基环境下的信号处理算法是星基ADS-B系统面临的重要技术挑战之一。

相干解调可以有效抑制噪声，是弱信号解调的有效途径之一。在相干解调算法实施的过程中，需要对接收信号的参数(频率和相位)进行较为精确的估计，而在低信噪比情况下估计信号的参数较为困难，是实现相干解调面临的主要问题。常用的信号频率估计算法主要是两步法：第1步是对要估计的信号进行快速傅里叶变换(FFT)，选取峰值作为信号频率的粗估计；第2步是精估计，利用比值法等方法进行信号频率精估计[5-7]。除两步法外，也有直接利用时域信号进行估计的算法[8]。这些算法在频率估计时都能取得良好的效果，但是缺点是不能同时估计信号的相位，Feng T和Liang J 提出基于遗传算法的频率相位估计[9]，可以有效解决低信噪比下信号参数估计，但是该算法的运算量较大，不利于工程上的实时计算。基于以上分析，本文提出基于幅度相位估计(APES)算法的弱ADS-B信号频率相位估计算法。首先对信号进行非相干解调并译码，找到信号的高置信度码位，之后利用高置信度码位处的信号集合对信号使用改进后的APES算法进行频率和相位估计，估计值可用于对信号重新相干解调，从而提高信噪比和正确译码概率。为了提高算法效率，本文介绍的方法先利用FFT对信号频率进行粗估计，使用APES算法进行精估计。仿真结果表明，在低信噪比和低采样率的情况下，算法达到了较高估计精度，且计算量相对较小。

1 信号频相估计方法

1.1 ADS-B信号格式

现行ADS-B系统的3种信号体制分别是1090ES数据链、VDL-4以及UAT数据链，其中1090ES数据链是目前应用最广泛的信号体制，同时也是被国际民航组织标准化的信号体制，因此本文针对1090ES信号格式的信号展开研究。

1090ES数据链信号的发射频率为1 090 MHz，允许存在1 MHz以内的偏差，信号帧长为120 μs，采用脉冲位置调制(PPM)。120 μs的信号帧长分为8 μs的报头信号和112 μs的数据域，报头包含4个前导脉冲，这4个脉冲分别位于0 μs、1 μs、3.5 μs和4.5 μs处，从第8 μs开始为数据位，数据位长112 μs，共有112位，每位包含2个码元。若脉冲位于前置位码元，则该码元表示本位为1；若脉冲位于后置位码元，则表示本位为0[10]，如图1所示。

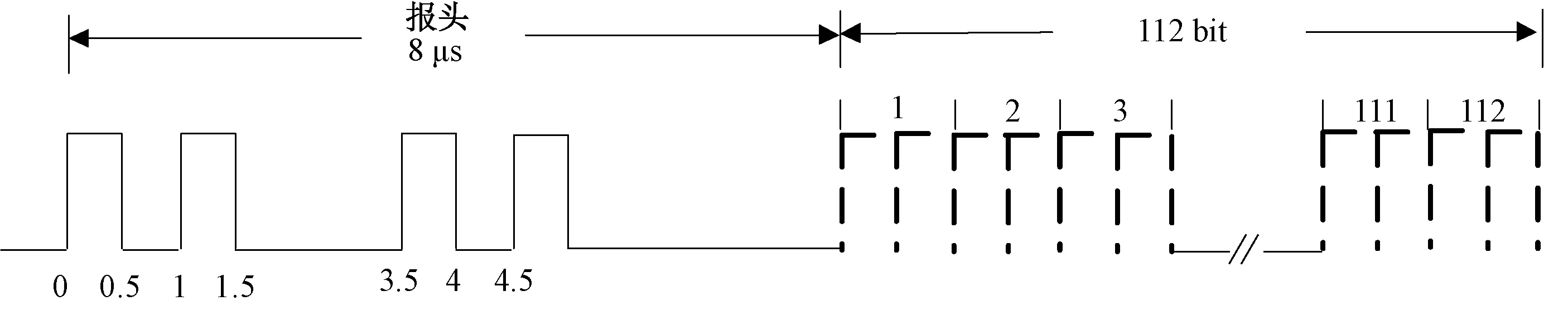
图1 ADS-B信号格式

1.2 APES算法简介

APES算法，也称为APES滤波器，用于信号的幅度和相位估计，于20世纪90年代被Li等人提出[11-12]。假设滤波器输入信号x(n)是复正弦信号加白噪声，则：

(2)

式中：v(n)为加性白噪声；αk和ωk分别为第k个信号的幅度和角频率，复幅度αk=|αk|ejφk，包含了信号的振幅和初相位。

现设计一个M个抽头的有限长单位冲激正响应(FIR)滤波器，使得期望频率为ω1的信号能够无失真地通过滤波器，同时极可能抑制信号x(n)中的其它频率分量和噪声。定义向量和滤波权向量：

x(n)=[x(n)x(n-1)x(n-2) …x(n-M+1)]T

(3)

w=[w0w1w2…wM-1]T

(4)

信号x(n)通过滤波器的输出为:

y(n)=wHx(n)=xT(n)w*

(5)

定义向量和矩阵：

(6)

(7)

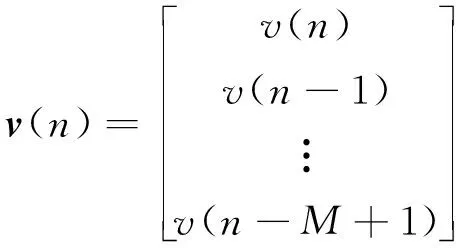
(8)

(9)

则有:

x(n)=As(n)+v(n)∈M×1

(10)

为了使期望频率为ω1的信号能够无失真地通过滤波器(即wHa(ω1)=1)，同时极可能抑制信号x(n)中的其它频率分量和噪声，即转化为下列约束优化问题:

st.wHa(ω1)=1

(11)

考虑更一般的情况，用ω代替ω1，则可对任意频率进行滤波，约束优化问题变为:

st.wHa(ω)=1

(12)

经推导，针对任意ω可得最优权向量为:

(13)

可得到信号复幅度α估计为:

(14)

(15)

(16)

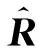
g(ω)定义如下：

(17)

(18)

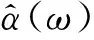
在使用APES算法时，要能对信号样本的相关矩阵进行准确估计；同时由于计算机计算幅度谱时是通过离散点描述的，若想提高精度则需要减小幅度谱离散点间隔，进而增加计算量。针对星基ADS-B信号，其调制方式造成信号在持续时间内不是连续的，并且在工程实施过程中采样率低，信噪比低，APES算法不能直接使用，下一节将给出解决方法。

1.3 星基信号估计方法

由1.1可知，当检测到ADS-B信号后，其调制方式决定检测到的信号不是连续的正弦信号，而是分段连续的相参正弦信号(每段是一个脉冲)，分段信号之间是由噪声填充，并且考虑到工程实施时译码采样率一般较低(1个脉冲即一段信号，一般只包含5个点)，若只用1个脉冲直接估计其频相，则相关矩阵估计得很不准确，并且因为是奇异矩阵，因此难以直接应用APES算法进行估计。

鉴于以上原因，考虑到实际上ADS-B信号的持续时间比较长，因此如果能利用所有有效脉冲信息去估计信号参数，则可以取得良好的效果。该方法的实现如下：

第1步，对混频后的低频信号进行采样，并进行非相干解调，求信号幅度和解码，若解码过后通过校验，则不需要进行相干解调，流程结束，若未通过校验，则进入第2步。

第2步，利用第1步中的解码结果，提取高置信度码位，作为第3步输入。

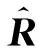
(19)

(20)

式中：D为ADS-B中高置信度脉冲的个数；ni为高置信度脉冲的位置。

第4步，对混频后的低频采样数据先进行FFT，再进行APES算法估计，利用APES算法来估计信号的频率和相位时，只需要计算FFT后频谱最高峰的左右峰之间的幅度谱即可，因此可大幅减少APES算法的计算量。

第5步，获得信号的频率和相位。

上述过程只利用了高置信度码位的信号来估计信号参数，在充分利用信息的同时，防止了低置信度码位噪声过大造成的影响，同时利用FFT减少了估计运算量，仿真分析表明该方法具有较高的精度和相对较少的计算量。

2 仿真分析

对算法进行仿真，取采样率为10 MHz，即每个脉冲含5个点，取高置信度脉冲个数为30个，基带信号如图2所示，幅度谱结果如图3所示。结果表明，在取幅度谱离散点较多时频率估计误差很小，相位误差约0.03 rad。

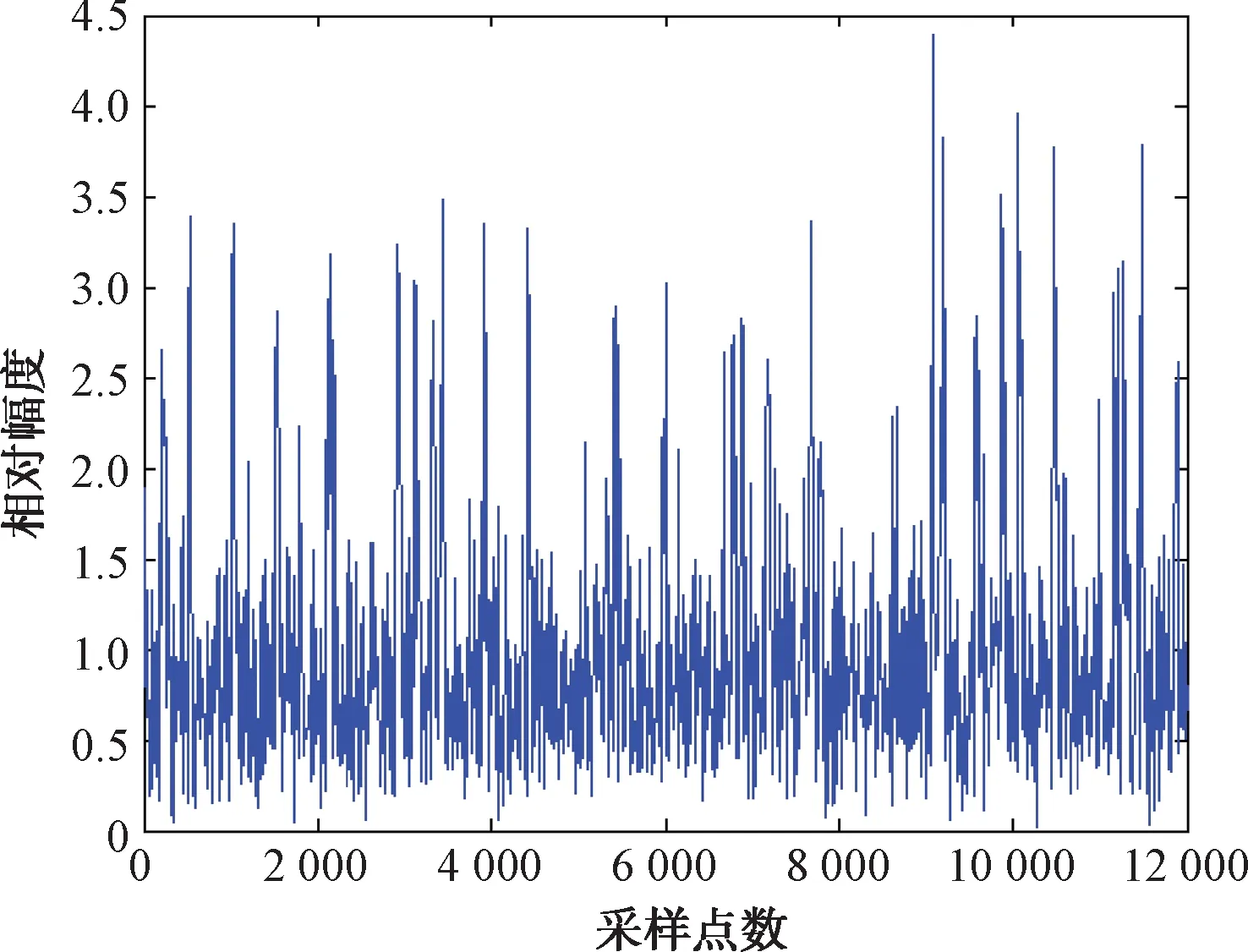
图2 基带信号

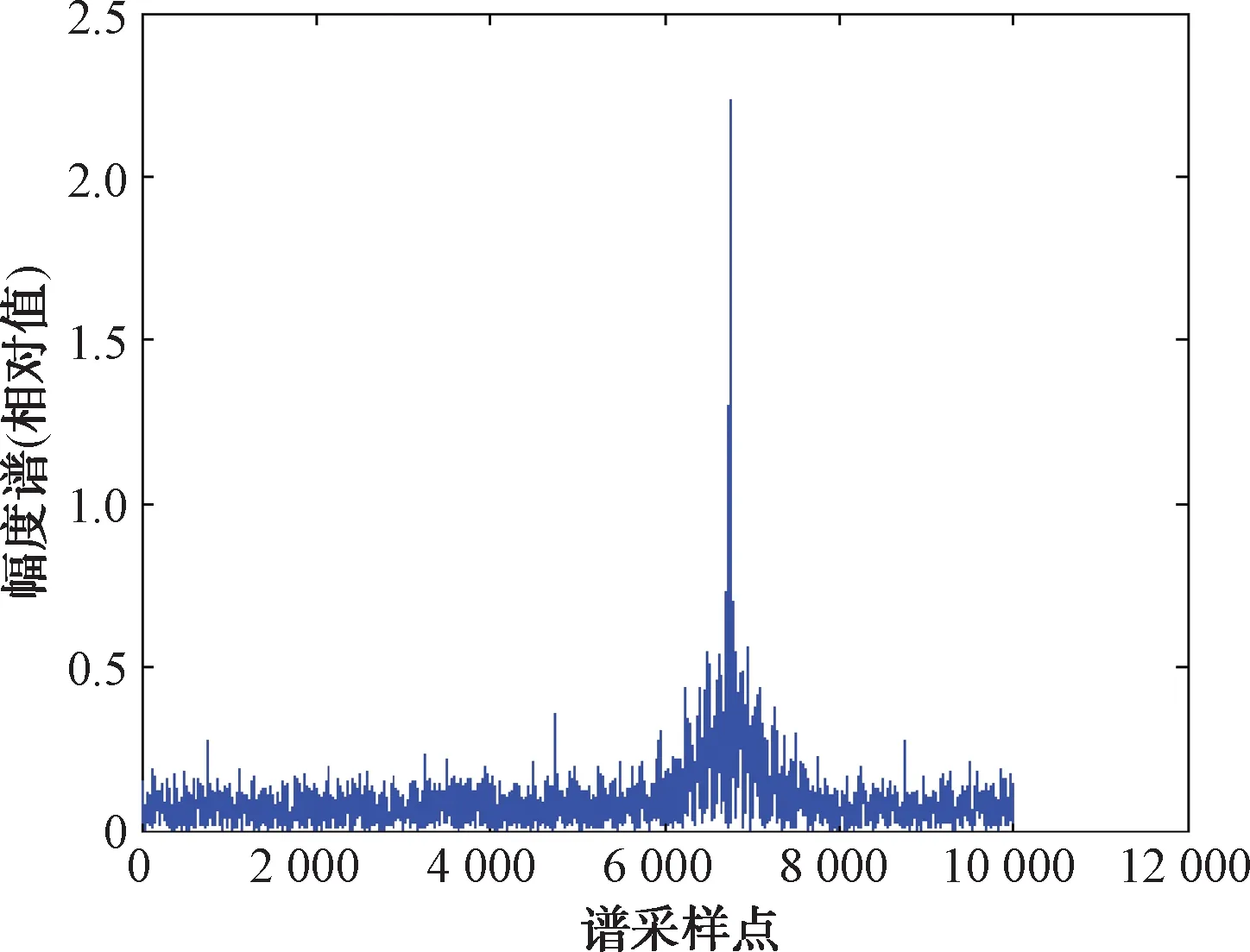
图3 D=30时算法性能

若把高置信度脉冲个数提高为50个，相位估计效果进一步提高，幅度谱效果如图4所示。

图4 D=50时算法性能

3 结束语

星基ADS-B系统是ADS-B系统的重要发展方向，相对于传统系统，该系统在安全性方面可提供覆盖全球的持续稳定的飞机监视能力,能够更好地支持安全管理系统，同时在效率和成本方面有较大提升。针对星基系统面临的挑战，本文介绍了一种基于APES算法的弱ADS-B信号参数估计方法。首先对信号进行非相干解调并译码，找到信号的高置信度码位，之后利用高置信度码位处的信号集合对信号APES算法进行频率和相位估计，估计值可用于对信号重新相干解调，从而提高信噪比和正确译码概率；同时利用FFT对信号频率进行粗估计，再使用APES算法对FFT峰值附近精估计，大幅减少了运算量。仿真结果表明，在低信噪比和低采样率的情况下，算法达到了较高估计精度。