基于改进拟牛顿法的柔性直流系统潮流算法*

邹建凯，韦延方

（河南理工大学电气工程与自动化学院，河南焦作 454003）

0 引言

基于电压源换流器的柔性直流输电技术（Voltage Source Converter Based High Voltage Direct Current，VSCHVDC）是新能源大规模并网和消纳的重要方式，但直流线路的引入使得变量数陡增，雅可比矩阵分解与求逆也变得异常繁杂[1]，这给潮流的快速求解带来了一定的困难。因此，如何有效地提升交直流系统潮流求解速率已经成为了现代电力系统发展不可忽视的问题。适用于柔性直流输电系统的潮流求解方法有统一法和交替法两种形式[2]。统一法是将交流和直流系统的各潮流方程联立求解，计及二者之间的耦合影响，对各种网络和运行条件都有良好的适应性[3]。交替法将交、直流系统潮流方程分别求解，对交流系统雅可比矩阵的改动小，可以有效地利用现有的纯交流系统潮流程序[4]。

现有的潮流求解方法大多基于经典的牛顿-拉夫逊（NR）法，经典NR 法在每次迭代中仅需一次三角（LU）分解[5]，同时具有二阶收敛特性[6]，可以有效地求解潮流问题。但随着电力系统规模的不断增大，尤其是VSCHVDC的馈入，变量数陡增，复杂的雅可比矩阵分解与求逆变得异常繁杂。Broyden 方法[7]作为一种经典的拟牛顿法，使用更容易计算的近似矩阵来代替复杂的雅可比矩阵，只需要在初始化时计算一次雅可比矩阵，减小了单步迭代计算量，但较低的收敛阶数使得其迭代次数有所增加。

为了提升潮流算法的计算效率，本文首先提出了适用于交直流系统潮流计算的Broyden 方法迭代形式，进而，针对该方法迭代次数过多的问题，提出了基于改进拟牛顿法[7]的潮流算法，该方法具备更高的收敛速度，在减少单步迭代计算量的同时又不会导致迭代次数增加过多，使得其计算效率得到了较大的提升。最后，对修改后的IEEE标准算例进行仿真测试，结果表明：本文算法具有与经典NR法相同的精确性，且其在计算速度方面更有优势。

1 VSC-HVDC的数学模型和潮流方程

1.1 VSC-HVDC的稳态模型及控制方式

单侧VSC-HVDC 系统的稳态数学模型如图1 所示[8]，其稳态方程已有相关研究[9]，本文在此不再一一赘述。

图1 VSC-HVDC稳态模型

电压源换流器具有多个可控变量，其中每个换流器可采用的控制策略如下：（1）有功功率Ps恒定；（2）直流电压Ud恒定；（3）直流电流Id恒定；（4）无功功率Qs恒定；（5）交流电压Us恒定。其中，有功功率Ps、直流电压Ud与直流电流Id可由移相角δ控制，无功功率Qs与交流电压Us由调制度M进行控制。本文所采用的4 种控制方式组合的方案详见文献[10]。

1.2 含VSC-HVDC的交直流系统潮流方程

基于交直流潮流算法的统一迭代形式与系统的稳态方程，将纯交流节点、直流节点、换流器VSC 的潮流方程进行联立，设系统总节点数为n，直流节点与换流器的个数为nVSC，交流节点的个数nac=n-nVSC，得到含VSC-HVDC的交直流系统潮流方程为：

式中：U、θ为节点电压幅值和相角；G、B分别为节点导纳矩阵的实部与虚部；上标s表示该功率为节点注入功率；i为节点编号；j∈i表示j节点与节点i相连；a 为纯交流节点；t为直流节点，其中1～nac为交流节点，nac+1～n为直流节点；Δd为换流器潮流方程；μ（0＜μ＜1）为换流器的直流电压利用率；M（0＜M＜1）为换流器调制度；Ud为直流系统节点电压；gd为直流系统节点导纳矩阵元素。

2 算法原理

2.1 Broyden方法原理

经典NR 法虽然可以达到二阶收敛速度，但每一步迭代需要计算n2个偏导数∂jfi(x(k))（i，j=1，2，…，n）及n个分量函数的值f（x（k）），其计算量是很可观的。因此，为了减少每步迭代的计算量，可采用Broyden 方法来解决非线性方程组的求解问题。Broyden方法是一种经典的拟牛顿法，这种方法的主要思想是用更容易计算的近似矩阵来代替复杂的雅可比矩阵，只需要在初始化时计算一次雅可比矩阵。Broyden秩1迭代公式[7]如下：

式中：函数f（x）为待求的方程；x（k+1）为第k次迭代后的修正值；sk-1=x（k）-x（k-1），yk-1=f（x（k））-f（x（k-1））；B0取f（x）在初始点x（0）的雅可比矩阵。

Broyden 秩1 方法将单步迭代计算量由O（n3）降为O（n2），大大地减少了计算量，一定程度上避免了误差的累计传播。但这种方法的收敛阶数低于经典牛顿法，为超线性收敛，会导致迭代次数的增多。

2.2 改进拟牛顿法原理

针对Broyden 方法收敛阶数较低，迭代次数增加等问题，文献[7]提出了一种改进拟牛顿法用于求解非线性方程组，第k次的迭代公式如下：

式中：dkB= -B-1kf(x(k))，dkM= -B-1kf(z(k))z(k)=x(k)+dkB，使用式（2）来更新Bk。

改进拟牛顿法使用了三阶NR 法的迭代形式，同时使用Broyden 方法更新其雅可比矩阵的近似矩阵，在一定情况下具有全局收敛性。该方法不仅保留了拟牛顿法单步迭代计算量小的优势，同时还能减少了迭代次数，使得其算法效率相较于经典NR 法与Broyden 方法而言有较大的提升。

2.3 含VSC-HVDC的交直流系统改进潮流

电力系统潮流计算的实质为非线性方程组的求解。在 此，设 VSC-HVDC 的 变 量 参 数 为x=[U,θ,Ud,Id,δ,M,Ps,Qs]T，而 各 不 平 衡 量 为 Δf=[ΔP,ΔQ,Δd1,Δd2,Δd3,Δd4]T，雅可比矩阵用J表示。电力系统潮流计算即为求解方程f（x）=0。利用下式计算功率不平衡量Δf：

基于改进拟牛顿法，可得改进的含VSC-HVDC 的交直流系统潮流混合算法求解过程如下。

3 算例分析

为了验证所提出改进潮流算法的有效性，同时对比改进算法与经典NR 法的计算效率，分别对14、30、57和118 节点的柔性直流输电系统进行仿真分析（算例系统均由IEEE 标准算例系统修改得到），使用MATLAB R2019b 进行测试，仿真精度ε设置为10-6。限于篇幅，本文主要分析验证了30 节点柔性直流输电系统的交流潮流结果和直流潮流结果，图2 为修改后的IEEE-30 节点交直流系统结构图，图中整流器与逆变器的参数设定相同，其 中XL=0.15p.u.，R=0.006p.u.，Rd=0.03p.u.，Xf=0.01p.u.（各参数均为标幺值）。

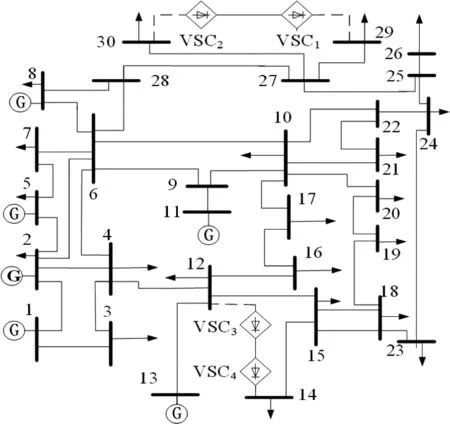
图2 经修改的IEEE-30节点交直流系统

3.1 基本算例测试

为验证所提算法在不同控制方式下的有效性和适用性，下面将分别对4 种控制方案进行仿真验证。为便于比较分析，设定A 表示经典牛顿法，B 表示Broyden 方法，C 表示改进拟牛顿法。上述方法具有相同的收敛精度，限于篇幅，表1、表2仅给出了IEEE-30算例系统在C方法下交流系统、直流系统潮流计算的结果。

表1 交流系统潮流结果（方案1）

根据表1和表2的仿真结果可知，改进拟牛顿法具有和经典牛顿法一样的高精确性；根据表2中4种不同控制方式下直流系统潮流结果可知，本文方法适用于换流器不同的控制方式及设定值。

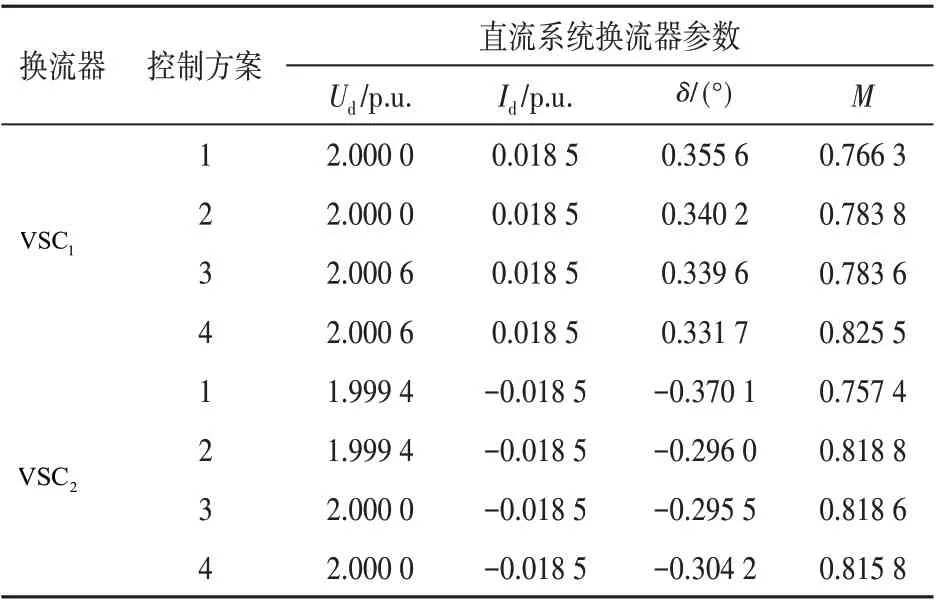
表2 直流系统潮流结果

3.2 算法效率测试

表3 为不同算例系统在方法A、B、C 下的计算性能比较（仅以方案1 为例）。由表可知，由于收敛阶数较低，方法B 的迭代次数相较于方法A 增加较多，因此虽然方法B 可以有效地减少单步迭代计算量，但其计算效率相较于方法A 提升较小，在各种算例情况下方法B 相较于方法A 的平均计算时间缩减率仅为8.371%；而方法C 在保留了低阶算法单步计算量较少优势的同时，减少了迭代次数，使得方法C 比A、B 两种方法计算时间更短，方法C 相较于方法A 的平均计算时间缩减率可达到26.712%。

表3 各算例迭代次数和计算时间比较（方案1）

对于全部算例系统而言，方法C 所用的计算时间最短。同时，当节点数从14 增加到118 时，方法C 的计算时间增量也是最短的。这说明方法C 在实际应用方面相较于经典牛顿法和Broyden方法具备一定的速度优势。

3.3 重负荷下算法性能对比

表4 为系统在重负荷情况下，方法A、B、C 的收敛性能对比（以IEEE-118 为例，控制方式为方案1，负荷改变的为节点44 的有功负荷，表中NC表示达到系统极限，算法不再收敛）。从表4 中可以看出，当负荷值从0.5 增加到2.992 时，3 种方法的迭代次数分别增加5、7、5 次，且方法C 的计算时间最少，仅为方法A 的一半左右，这表明方法C 在极端条件下具有很高的稳定性与高效性。

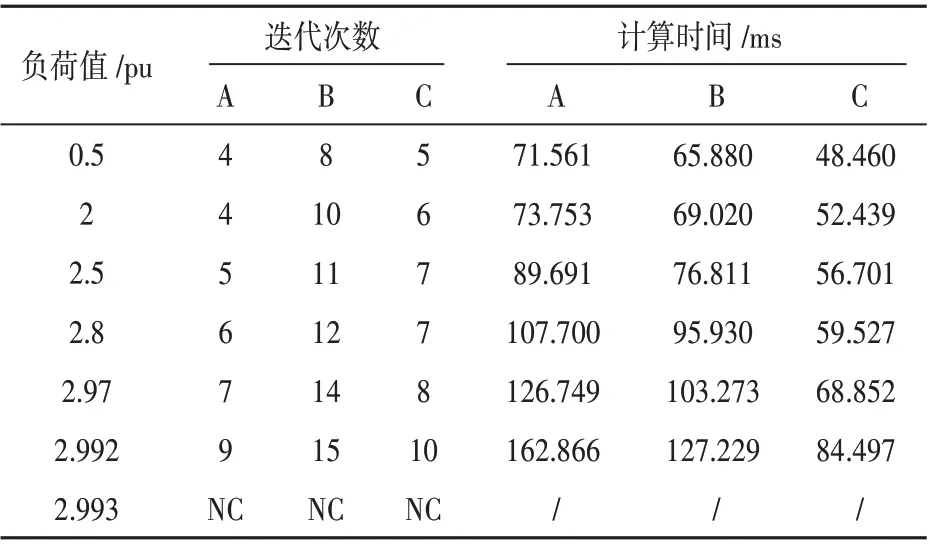
表4 重负荷下迭代次数和计算时间比较（方案2）

4 结束语

基于电压源换流器的柔性直流输电技术是新一代高压直流输电技术，它相较于传统高压直流输电具有多项技术优势。本文针对柔性直流输电系统，提出了一种基于改进拟牛顿法的柔性直流系统潮流算法，该算法在每次迭代中不需要计算复杂的雅可比矩阵，而是使用更容易计算的近似矩阵来代替，极大地减少了计算量，同时保持了较高的收敛阶数，使得算法效率相较于经典牛顿法和Broyden 方法得到了显著的提升。同时，算例结果也验证了本文提出的改进拟牛顿潮流算法的可行性与有效性。