基于组合混沌的多精度流加密方案*
2023-03-22周宇李巧刘静王骏超
周宇,李巧,刘静,王骏超
(1.中国信息通信研究院西部分院,重庆 401336;2.联合微电子中心有限责任公司,重庆 401332;3.重庆大学微电子与通信工程学院,重庆 400044)
1 引言
混沌是一种具有内在随机性的非线性动力系统,具有对初始值敏感性、遍历性、伪随机性、轨道不可预测性的特点[1],常作为伪随机序列发生器应用于密码系统中。但是,在计算机有限精度下实现混沌系统得到的序列随机性下降,抗干扰、抗截获的能力不高[2]。浮点系统可以保留混沌特性,但增加了系统的计算量与硬件开销,而定点混沌系统动力学退化效应目前没有衡量指标,应对混沌动力学退化的方案有添加随机扰动、提高数据精度等[3]。添加随机扰动在具体应用过程中实现方法简单,有利于提高动力学特性[4-8]。
文献[9]将多个混沌块级联在一起,以产生具有更好随机性的伪随机数。中南大学的科研团队详细研究了混沌序列复杂性的分析方法,比较了近似熵、谱熵、样本熵和强度统计复杂度等算法,这些方法可以为混沌在有限精度条件下的应用提供相关理论依据[10-11]。本文提出了基于组合混沌的多精度流加密方案,并用谱熵作为定点混沌的混沌评判方法。
2 混沌系统
2.1 Logistic 映射
Logistic 映射是一个被广泛研究的一维离散映射,也称为虫口模型,其表达式是一个简单的非线性迭代方程[12],通过向下取整可以保留有限精度,其定义为:
式中O 代表选择的数据进制,这里为二进制,c 为数据精度,此处为常数,可取定点32 位、24 位、16 位、12位,n 为迭代次数。结构参数μ∈[3.569,4]时,系统进入混沌状态。此时系统迭代产生的序列是非周期且不收敛的伪随机序列。μ 越趋近于4,迭代产生的值在区间[0,1]内越接近均匀分布。
2.2 Tent 映射
Tent 映射是分段的二维混沌映射,与Logistic 映射互为拓扑共轭映射,其应用比较广泛[13],取整后的表达式为:
式中结构参数α∈[0,1],yn∈[0,1],当α=0.5 时,系统呈现短周期状态,且系统的初始值不能与α 相同,否则迭代产生的序列出现周期,系统演化为周期系统。
2.3 谱熵
通过向下取整函数可以得到定点混沌序列,然而取整函数舍弃了部分小数位,降低了数据精度,系统每次迭代都会受到影响,精度损失过大会导致混沌系统进入周期状态或者丧失不确定性。失去混沌动力学特性将导致序列的随机性减弱,影响加密效果。
对序列随机性进行定量分析可以评估系统的安全性。用定点序列进行加密显然可以降低系统的计算复杂度,然而通过式(1)可以看出,目前混沌评判指标如Lyapunov 指数存在求导过程,无法适用于定点系统,而K 熵、庞加莱截面等方法也难以实施。谱熵通过频域内能量谱特性来分析序列的复杂程度,可以直接用快速傅里叶变换算法得到频域特性,在频域内序列的能量谱分布越均衡,随机性越强[14]。结合香农熵可以计算出相应的谱熵值(SEN)。
(1)去除序列直流部分。
(2)进行离散傅里叶变换,求得傅里叶系数X(k),k=0,1,...,N-1。
(3)计算X(k)的前半部分序列不同点的功率谱Pk、序列在k 点处的功率p(k)及序列总功率Ptot,k=0,1,...,N/2-1。
(4)计算序列谱熵s 并取得归一化的谱熵值S。
3 基于组合混沌的数据加密算法
3.1 密钥生成
本系统的密钥为α0和μ 两个结构参数、Tent 映射初始值y0和每轮迭代次数l,这些密钥由通信双方确定。混沌初始值由密钥加上明文图像通过哈希函数得到的哈希值组成。哈希函数对初始值敏感的特性可以保证系统对明文敏感。混沌系统参数为α、μ,y。通过明文和SHA-256 函数生成长度为256 位的二进制序列H,它被分成32 段,长度为8 位。Tent 映射的初始值计算公式如下:
3.2 组合混沌随机数发生器
组合混沌序列产生流程如图1 所示。首先选择数据精度,依据数据重要程度的不同可以选择浮点数及定点32 位、24 位、16 位和12 位数。再交换密钥后生成混沌系统的初始值,本文提出通过改变Logistic 系统初始值的方式来打乱序列的生成规律,序列经过l 次迭代后,将得到一个新的初值。每次的初始值由Tent映射迭代生成,即Tent 映射迭代一次生成Logistic 的初值,每得到一个初值后Logistic 映射迭代l 次。Tent迭代生成的序列也是随机的,提升了轨道的不可预测性,进一步提高了序列的随机性。
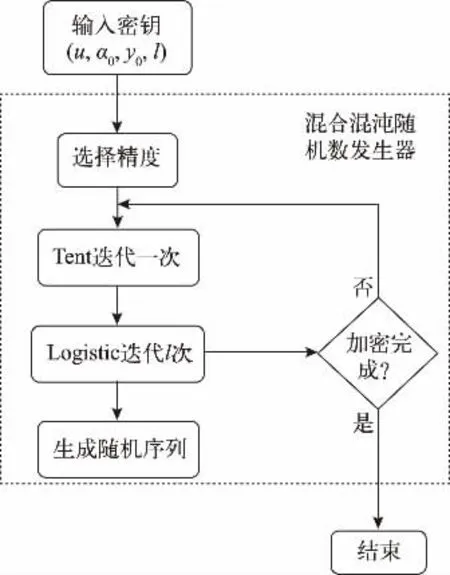
图1 组合混沌序列产生流程
3.3 组合混沌系统加密流程
本文提出的加密流程如图2 所示。通过保留不同的精度,可以得到安全性不同的加密系统,保留精度越高,序列随机性越强。通过组合混沌系统可以在定点状态下产生性能良好的伪随机序列xn,经过式(12)所示的门限判断得到加密用的二进制序列Sn,Sn与明文In进行异或操作得到二进制密文序列Zn。
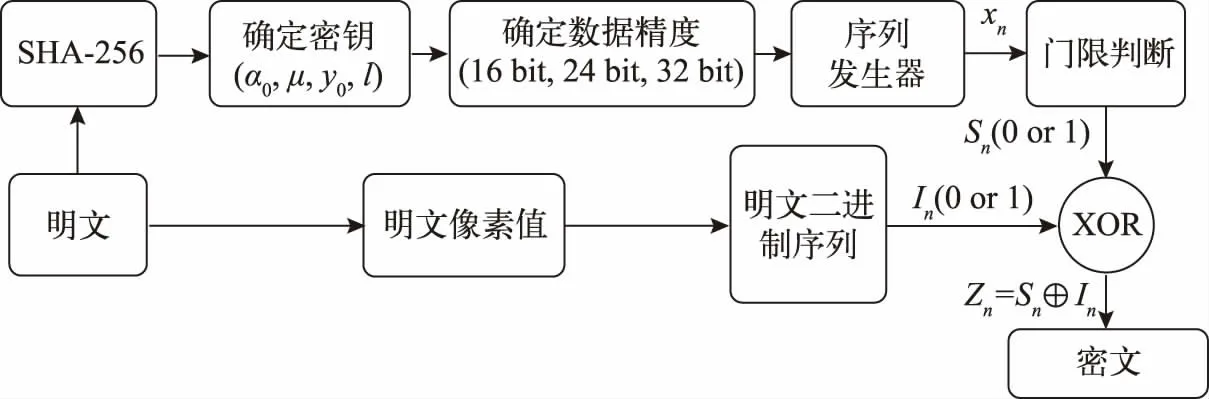
图2 组合混沌加密算法流程
4 系统安全性测试分析
4.1 序列自相关性分析
序列的自相关函数可以有效衡量信号是否具有随机性,具有良好随机性的序列的自相关函数类似于δ 函数。组合混沌序列与单混沌序列的自相关性对比如图3 所示,混沌初始值及结构参数:x0=0.1,μ=4,α=0.499。组合混沌初值中y0=0.6,l=1024,得到的序列长度都为512×512×4。从图3 可以看出,精度越低序列自相关性越强,但在有限精度影响下低精度序列开始出现类周期现象。组合混沌系统有效克服了周期效应,序列自相关函数具有良好的类δ 特性。
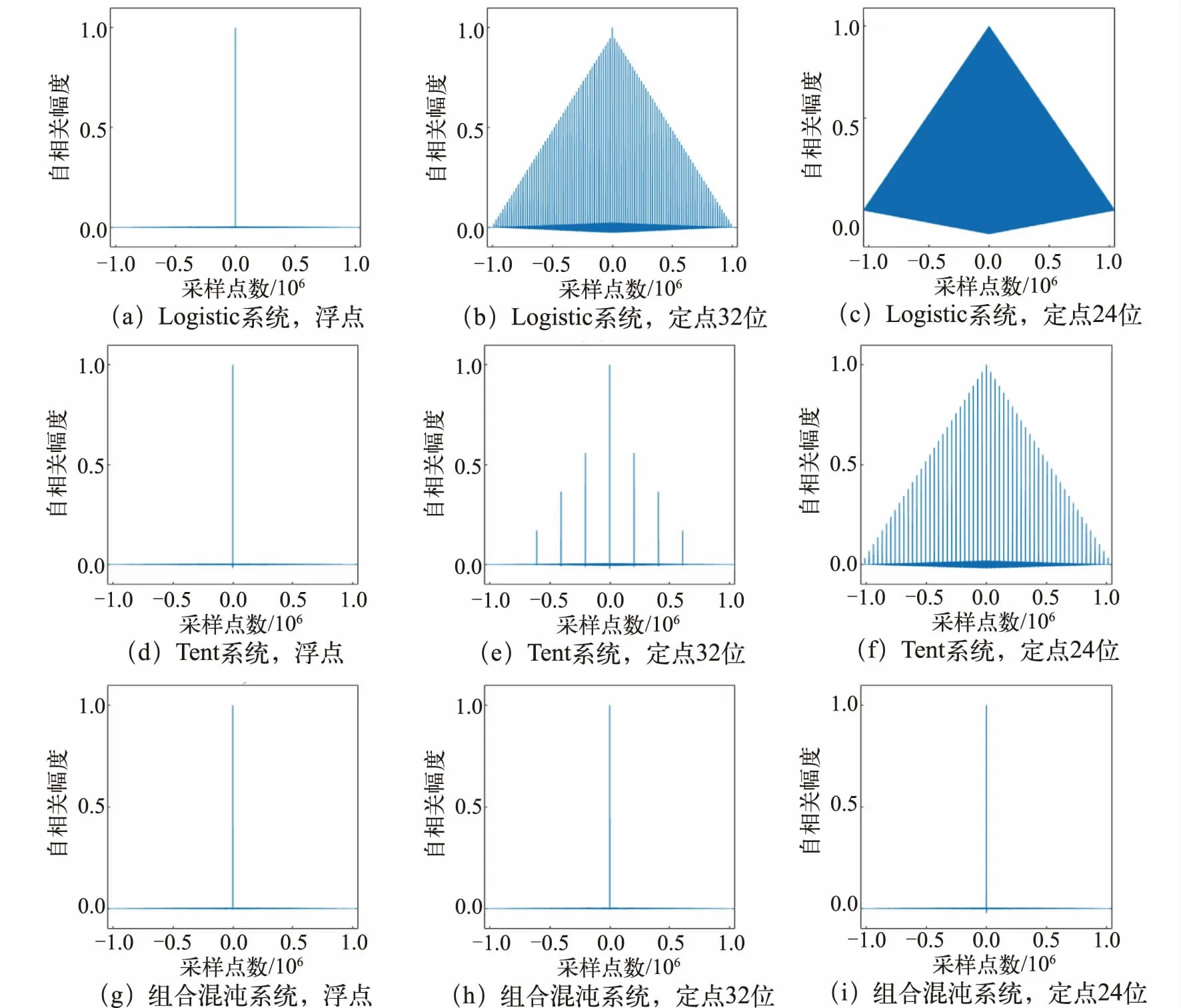
图3 序列自相关性对比
4.2 谱熵分析
本文以谱熵值作为衡量定点混沌动力学退化程度的指标,当定点数系统序列谱熵值与浮点数接近时,表明系统保留了混沌特征。系统长时间演化之后轨道进入吸引子附近,可能造成类周期现象,因此迭代长度对序列随机性也有一定影响。
不同系统的谱熵值随迭代次数的变化情况如图4所示,可以看出单混沌定点系统在通过多次迭代之后出现谱熵值减少的现象,说明系统随机性下降。当精度为24 位时,组合混沌系统产生的混沌序列的谱熵值为0.903 7,此时l=1 024,谱熵值接近浮点序列。当精度增加到32 位时,谱熵值为0.954 7,但此时l=16 384,说明组合混沌的定点24 位、32 位系统性能接近浮点系统,组合加扰的方式增加了生成序列的随机性。因此,当有效精度保持率较高时,l 值可以取得更大。在本文的性能分析中,选择l=1 024。
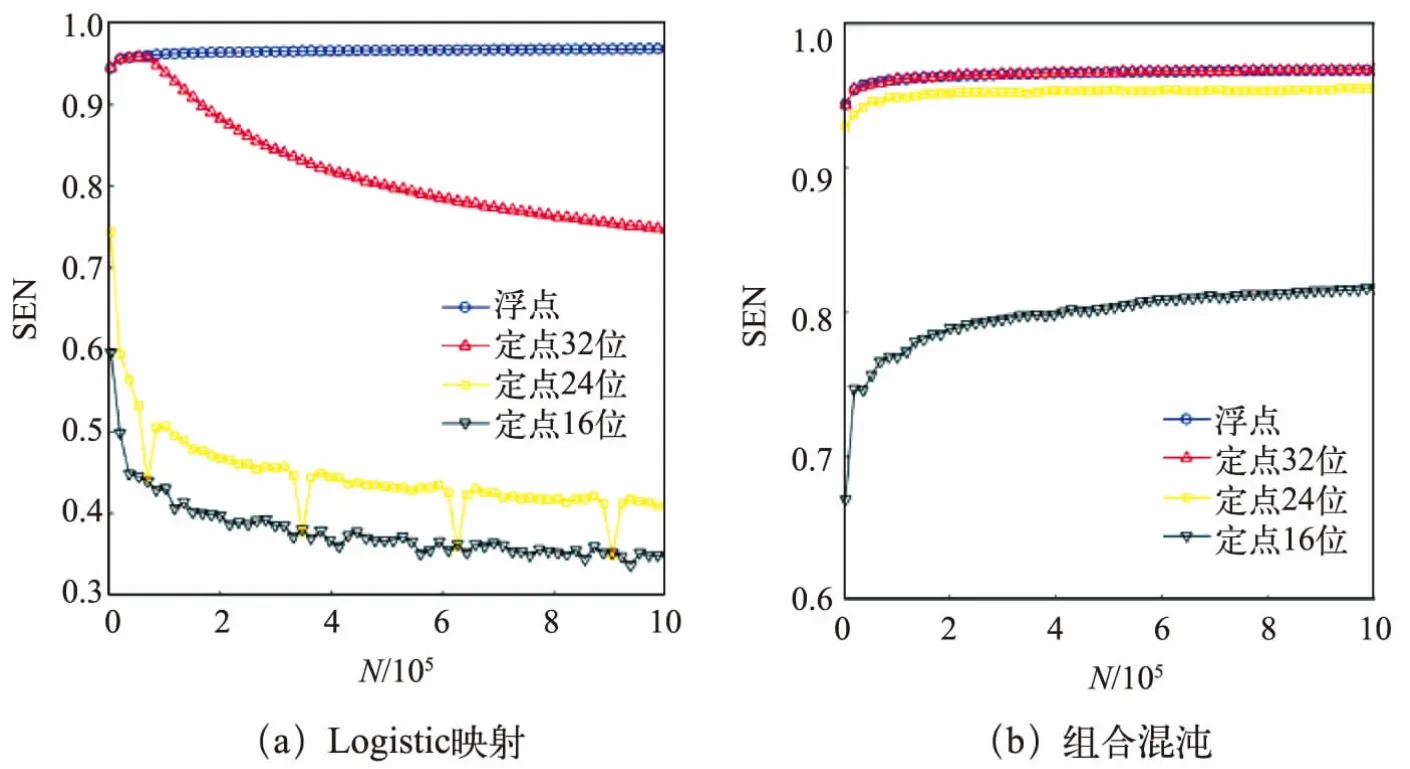
图4 不同系统谱熵值分析
4.3 NIST 测试
NIST 测试广泛用于检测二进制序列的随机性,包含15 个测试[15]。每项测试最终输出统计结果参考值Q,当Q>0.000 1 时表示通过该项测试。混合混沌系统产生的长度为106的二进制序列和相同长度的单个Logistic 混沌生成的二进制序列的NIST 测试结果如表1 所示。可以看出,单混沌浮点系统可以通过所有测试,而单混沌定点32 位系统只有部分统计通过检验,而组合混沌生成的32 位定点系统生成的序列可以通过测试。
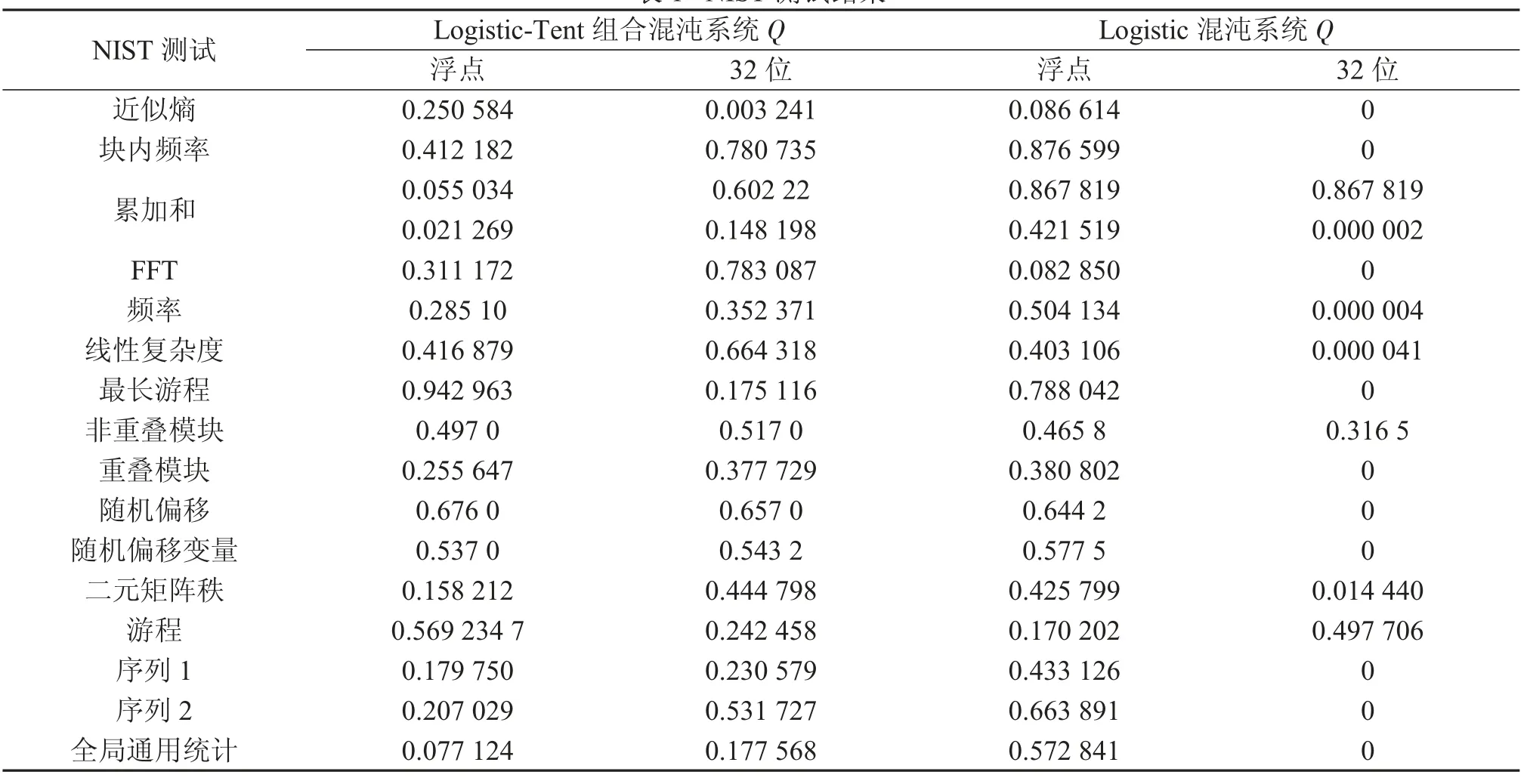
表1 NIST 测试结果
4.4 加密安全性测试
选取不同图片进行加密效果分析,不同明文加密效果如图5 所示,CT 图像(Covid-19 病患的肺部)的大小为512×512×3,其他图像的大小为512×512。

图5 不同明文加密效果
所提出的不同精度加密系统加密算法的安全性测试结果如表2 所示,NPCR 为像素变化率,UACI 为统一平均变化强度。测试图像为标准加密图像Lena,手段包括信息熵分析、抗差分攻击分析、加密效率分析,对定点混沌加密系统与浮点加密系统进行了详细的对比分析。

表2 不同精度系统加密安全性分析
从表2 中看出,组合混沌定点32 位与24 位系统加密效果接近浮点系统,可以有效加密明文图像,同时系统加密效率高,对于数据量较大的图像可以快速完成加密。组合混沌加密算法与其他混沌加密算法的对比结果表明,组合混沌加密算法具有良好的安全性,可以有效抵抗攻击。
5 结论
本文研究了数字混沌系统在加密算法中的应用。采用基于Logistic 映射和Tent 映射的混合混沌伪随机序列发生器可获得性能良好的伪随机序列,加密算法支持选择不同的加密精度,包括浮点、32 位定点、24位定点和16 位定点。混合混沌系统得到的24 位和32位序列的性能接近于浮点序列。本文提出的算法提高了加密效率,能够抵抗常见的攻击手段。同时,提出将谱熵作为定点混沌的动力学量化指标,可以直观比较定点混沌序列与浮点序列的性能,作为定点系统混沌动力学退化的衡量指标。
