兼顾多元表征的APOS数学概念教学探究

杨兴 武慧虹 钱淑渠

【摘 要】文章在分析多元表征理论和APOS理论内涵的基础上，寻找其相容性和互补性，建立兼顾多元表征的APOS循环模型来刻画概念学习的心理过程。兼顾多元表征的APOS数学概念教学包括一个前提“分析概念的表征系统”和四个环节“创设问题情境、抽象概念程序、凝练数学对象、完善概念意象”。

【关键词】APOS理论；多元表征；概念教学；数学概念意象

新的数学方法和概念，常常比解决数学问题更重要。新授课的概念教学是数学教育研究领域的热点。美国学者杜宾斯基提出APOS理论，认为数学概念的学习要经历活动（Actions）、程序（Processes）、对象（Objects）、图式（Schemas）四个阶段。该理论刻画了学生学习概念的心理过程和概念建构的层次性而被广泛运用于数学概念教学中［1］。由于学生经验背景的差异，不同学生对同一概念有不同表征，有些学生喜欢言语性材料的学习，有些学生则喜欢空间性材料的学习［2］。数学概念的学习应是多元化的，但基于APOS概念教学的现有研究中，很少关注概念的多元表征。Font等人指出数学教育界的一个特点是理论观点的多样性，我们需要找到理论之间的联系，以便找出是否具有潜在结构能联系各理论［3］。近年来已有学者以APOS理论、多元表征理论与变式教学理论为基础，尝试探寻三者的共同特征与联系，将三者“凝聚”于数学概念教学设计之中［4］。研究发现，多元表征理论与APOS理论之间存在一定联系与区别，将两种理论取长补短，并进行适切融合，既能提升教学的效果，也有利于教育理论的发展。因此，各取两种理论所长，兼顾多元表征，改进基于APOS理论的数学概念教学过程，能促进学生数学概念的学习。

一、多元表征理论与APOS理论的相容性和互补性

（一）两种理论的相容性

两种理论的相容性指的是两者没有矛盾冲突的地方，并且在某些方面存在一致性，可以相互协调，融合发展。本文所指的“相容性”体现在都强调概念意象的形成。Tall和Vinner最早将概念定义和概念意象进行区分并用来描述学生对数学概念的理解［5］。事实上，我们在理解和应用概念时，往往用的是概念意象而不是概念定义，例如，当谈到矩形的概念时，我们首先想到的不是“一个角为直角的平行四边形是矩形”，而是在头脑里浮现一个四个角是直角的四边形。简言之，相对于概念定义而言，概念意象是一个更加具体、随意且灵活的综合心理表征，数学概念教学的目标不只是对数学概念定义的简单记忆和运用，更要帮助学生建构属于学生自己的数学概念意象。

多元表征理论下的概念教学就是基于学生已有的概念意象呈现不同的概念表征形式，通过表征间的转换，从不同角度豐富对概念的理解，建立新的概念意象。例如上文提到的矩形概念，不仅是让学生掌握矩形的各种标准定义，还要在头脑里形成矩形的图象、符号化表征。而APOS理论指出了学生建构概念图式的层次，从多元表征的角度可以把图式理解为一个包含了数学概念的操作、情境、图象、符号、定义等多元表征的系统。换言之，概念图式可以理解为概念意象，概念图式的建立依赖于概念表征之间的相互转换。由此可见，两种理论对数学概念教学的目标是一致的，都强调建立数学概念意象，教师可以结合两种理论来分析数学概念的教与学。

（二）两种理论的互补性

一方面，APOS理论既指明了概念学习的层次，即由浅入深，由具体到抽象，从动态到静态，也突出了概念学习的最终结果，即建立概念意象，着眼于整个概念教学过程，侧重概念建构的中观层面。Borji等人认为APOS理论与其他认知理论一样，它仅限于对构成该理论的心理结构进行预测和描述，这些似乎不能充分说明所研究的现象［6］。由于学生认知风格的差异性，不同学生在每个阶段的概念表征方式不同，而APOS缺乏对概念表征微观层面的关注，从而导致基于APOS理论的概念教学效果各异。另一方面，多元表征理论强调数学概念意象的操作、图象、情境、语言、符号等具体表征之间的转换，着眼于概念教学的局部操作，侧重概念建构的微观层面，但对概念学习过程的整体性关注不够，也没有体现各表征转换的层次性和循序渐进性。

可见，微观层面的多元表征理论与中观层面的APOS理论相辅相成。在学习概念的多元表征时，教师可以借助APOS理论明晰学生的心理结构，从而设计合理的数学表征。在运用APOS理论设计概念教学时，兼顾概念的多元表征，有利于不同认知风格的学生提升学习效果，此外，多元表征间的转换也能促进图式的完善。因此，着眼于概念教学局部的多元表征理论需要整体性的引导，着眼于概念教学整体的APOS理论也需要局部性的支撑，整合多元表征理论和APOS理论的概念教学是符合部分和整体的辩证关系。

二、兼顾多元表征的APOS循环模型

众所周知，教育教学活动应考虑学生的心理过程，既然多元表征理论与APOS理论存在一定相容性和互补性，都强调数学概念意象的建构，尊重学生概念表征的差异，那么在兼顾多元表征的APOS数学概念教学中，概念学习的心理过程是怎样的呢？笔者在APOS循环的基础上，结合多元表征理论设计了兼顾多元表征的APOS循环模型（如图1）。该模型刻画了学生在学习数学概念时脑海里涉及的心理结构和心理机制，以及多元表征对形成相应心理结构的作用。

首先，由“活动—程序—对象”组成的APOS循环揭示了概念建构的层次，是学生在学习概念时的思维主线；其次，概念的多元外在表征促进外在操作活动内化为心理操作程序，再通过多元内在表征的精简进一步“压缩”为一个数学对象，初步获得数学概念（定义）；再次，多元表征间的转换，实现了“活动—程序—对象”的真正循环，包括正向和反向的；最后，在生成概念的基础上，形成概念的表征系统，并通过不同表征间的转换建构起图式，即概念意象。

三、兼顾多元表征的APOS数学概念教学设计

不同于概念定义的一成不变，概念意象处在不断地变化、发展和完善的过程中，不可能通过一两次的教学就能帮助学生建立概念意象。因此，借鉴喻平教授提出的概念域和概念系［7］，完善概念意象的教学至少还包括两个方面：一是掌握这个概念所有的等价定义并建立它们之间的联结；二是建立这个概念与相关概念之间的联结。这个过程可以在“图式”阶段实施，也可以作为后续完善概念意象的教学。

因此，兼顾多元表征的APOS数学概念教学是以“分析数学概念的表征系统”为前提，将该表征系统与兼顾多元表征的APOS循环适切融合，以完善数学概念意象为目标，以教师呈现概念的多元表征形式和学生掌握概念的多元表征为落脚点，形成以“创设问题情境—抽象概念程序—凝练数学对象—完善概念意象”为单元的循环过程，如图2所示。

（一）分析概念的表征系统

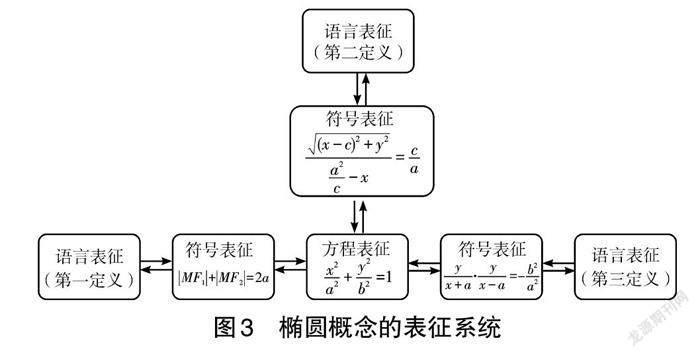
在教学设计之前，教师可结合学生已有知识经验和数学概念的特征，分析概念的表征系统，包括内在表征和外在表征。图3是椭圆三种定义构成的椭圆概念的表征系统，以第一定义引入为例展开教学。

（二）创设问题情境

根据概念表征系统的外在表征创设数学问题情境，呈现数学概念的外在表征形式，引导学生进行观察、操作，初步建立新概念与已有知识经验之间的联结，形成对数学概念的感性认识。

情境1：太阳光下球的影子、行星绕太阳运行的轨迹、用一个不垂直于圆锥的平面截圆锥……这些是什么图形/轨迹/曲线？

情境2：让学生用细绳和铅笔画橢圆（过程略）。画出的轨迹是什么曲线？在这一过程中，移动的笔尖（动点）满足的几何条件是什么？

情境3：教师用几何画板或GeoGebra软件演示形成椭圆的动画，注意引导学生观察变与不变的量。你有什么发现？当动点满足什么条件时，它的轨迹是椭圆？

【设计意图】以上三种情境涉及椭圆的图形表征和操作表征，需要学生在直观感知椭圆形状的基础上，动手绘制椭圆，借助动画演示观察椭圆，形成对椭圆概念的感性认识。

（三）抽象概念程序

教师组织学生通过自主思考、合作探究等方式，从活动情境中反思数学概念的形成过程，抽象出数学概念的形成程序，实现数学活动的内化，将数学概念的外在表征转换为内在表征。

师：椭圆上的点满足的几何条件是什么？小组讨论交流。

生：椭圆上的点到两定点的距离之和为常数。

师：你能用数学语言表达出这一数量关系吗？请写出你的表达式并与你的同桌进行交流，你有什么发现？

生：[MF1]+[MF2=2a]（[a>c]）。

（在实际教学中，学生的表达式可能各不相同，需要教师纠正、统一。）

【设计意图】教师组织学生进行讨论和探究，思考椭圆的形成过程，引导学生概括出椭圆上点的几何性质，从而抽象出椭圆定义的自然语言表征，再用符号进行表示，从而得到椭圆定义的符号化表征，将椭圆形成的外部活动内化为抽象的代数程序。

（四）凝练数学对象

教师让学生用数学符号语言翻译数学概念的形成程序，并进行运算和化简，从而将数学概念的内在表征精简为一个更简洁、更具有知识结构的符号化心理对象。例如教师可引导学生比较、讨论各自推导的方程形式，从而解决以下问题：（1）怎样建系？（2）如何运算、化简？（3）焦点在y轴上的标准方程怎样推导？它们有何联系？

【设计意图】教师引导学生根据椭圆的对称性建立合适的直角坐标系，将椭圆定义的符号化表征[MF1]+[MF2=2a]（[a>c]）翻译为代数表达式[（x+a）2+y2]+[（x-a）2+y2=2a]，进而化简得到椭圆的标准方程，建立椭圆的几何特征与数量关系的有机联系。

（五）完善概念意象

该教学环节主要有两个方面：一是教师可以设计变式训练、概念辨析等环节，帮助学生巩固、应用所学概念，建立这个概念与相关概念之间的联结；二是根据概念的等价定义创设新的教学情境，从不同角度得到同一个概念，从而完善学生的概念域和概念系。

例如，椭圆第三定义的教学有两个角度。一是从一个特殊轨迹来寻找它的方程。

设A，B两点的坐标分别为（-5，0），（5，0），直线AM，BM相交于点M，且它们的斜率之积是-[49]，求点M的轨迹。

二是从椭圆的标准方程出发来研究轨迹。

将椭圆标准方程[x2a2+y2b2]=1（a[>]b[>0]）进行适当变形得到[yx+a·yx-a=-b2a2]（x[≠±a]）。你能解释这个表达式的几何意义吗？

【设计意图】经过前面三个阶段，学生已建立起与椭圆第一定义相关的概念表征。接下来需要进一步完善概念意象，掌握形成椭圆的各种方式，理解各种椭圆定义之间的区别和联系，灵活选择条件求出椭圆的标准方程。

四、结语

以椭圆为例，基于椭圆的三种定义建立概念表征系统，根据第一定义创设问题情境，抽象出椭圆定义的符号化表征，进而凝练椭圆的标准方程，最后通过变式训练、概念辨析和等价定义完善椭圆的概念意象。当然，椭圆概念意象的完善不仅限于此，还需要把握椭圆概念与其他相关概念之间的关系，比如椭圆与圆有何关系？如何通过圆上动点得到椭圆的轨迹？探究类似问题亦可作为完善椭圆概念的途径。

近年来，数学教育理论不断推陈出新，单元教学、深度学习、项目合作学习等教育改革，都在努力践行素质教育理念，希望实现减负增效提质。但没有一种理论可以涵盖所有的教学情境，每一种教育理论都有其优势与独到之处。因此，兼顾多元表征的APOS数学概念教学不在于提供一整套教学模式，而在于让大家关注多元表征与APOS相辅相成，即根据数学概念表征的差异和数学概念学习的心理过程，设计满足学生不同认知风格的教学过程，提供所有学生参与学习的机会。只有不断挖掘各教育理论之间的联系，才能让我们的教学游刃有余，学生的学习如鱼得水。

参考文献：

［1］鲍建生，周超.数学学习的心理基础与过程［M］.上海：上海教育出版社，2009.

［2］喻平.数学教育心理学［M］.南宁：广西教育出版社，2004.

［3］FONT V，TRIGUEROS M，BADILLO E，et al. Mathematical objects through the lens of two different theoretical perspectives：APOS and OSA［J］. Educational studies in mathematics，2016（1）：107-122.

［4］李彩红，李祎.基于三种学习理论整合的数学概念教学设计［J］.数学通报，2014（5）：19-23.

［5］TALL D，VINNER S. Concept image and concept definition in mathematics with particular reference to limits and continuity［J］. Educational studies in mathematics，1981（2）：151-169.

［6］BORJI V，ERFANI H，FONT V. A combined application of APOS and OSA to explore undergraduate students’ understanding of polar coordinates［J］. International journal of mathematical education in science and technology，2020（3）：405-423.

［7］喻平，单墫.数学学习心理的CPFS结构理论［J］.数学教育学报，2003（1）：12-16.

（责任编辑：陆顺演）