基于聚类关联规则神经网络组合算法的弹丸初速预测

田珂

(63861部队， 吉林 白城 137001)

收稿日期：2021-10-18

0 引言

靶场测试某型脱壳穿甲弹炮口初速的试验中，由于该型试验任务是射表试验，需要使用两台初速雷达同时测试弹丸的炮口初速。每发弹丸会测试到两个初速数据，然后根据这两个初速数据的平均值检验弹丸的相关性能和对应指标是否满足定型要求[1]，因此两台雷达测试炮口初速的准确性关系到能否对武器装备进行准确鉴定。试验中有时遇到雷达死机、红外未启或误启、火炮工况异常、弹丸异常或者人为失误等突发情况时，某台雷达就会需要重构相应的初速数据或者测试的初速数据不准确。由于该种弹丸必须在0.5 h内射击完毕，如果出现重构数据、无效数据或者试验时间超出了0.5 h，就必须重新射击一组弹丸重新试验。

由此可见，利用科学合理的方法预测出重构的或不准确的初速数据，就成为一项必要的工作。目前研究预测弹丸初速的文献有很多[2-5]，这些文献从不同角度和应用场景研究了如何利用潜在的规律预测弹丸初速并且提高精度，但是当样本数据非常大时，如何正确处理异常值和重构值，样本数据的质量对预测精度的影响有多大，这些文献研究的并不多，尤其是在两台初速雷达同时参试时，如何利用一台雷达的数据预测出另一台雷达的数据，尤其是如何挖掘出优质样本进而提高预测弹丸初速的精度等方面的相关文献还不多，这是因为样本数据的质量决定着所建模型的好坏，模型的好坏又关系到预测精度的高低[6]。由于两台初速雷达是同时参试的，其测试的大部分初速数据基本一致，但还是存在一些测试不准确的数据即异常值，也存在一些没有测上的数据即重构数据，如果把这两种数据包含在样本数据中，则所建模型和预测出的数据必然是不准确的，因此必须从样本数据中剔除掉异常值和重构值，挖掘出测试一致性较好的数据，并把这些数据作为样本数据进行建模预测。

试验中假设参试的两台雷达分别为雷达A和雷达B，测试的是同一发弹丸的炮口初速，具有一定的内在关联性，而试验中雷达B的数据存在重构的情况，因此选择雷达A相对火炮的左正、后正及测试的初速数据作为输入向量，雷达B测试的初速数据作为输出向量，利用挖掘出的样本数据建立反向传播(BP)神经网络模型，然后把雷达B没有测上而雷达A测上的初速数据及左正、后正等数据代入建立好的模型中，就可以预测出雷达B重构的或测试不准确初速数据。由于BP神经网络具有非常强的非线性映射能力，大量的样本数据会增强模型的泛化能力和稳定性，鲁棒性也会增强，正好适合预测弹丸的炮口初速。

本文建模预测的总体思路是：首先利用聚类分析关联规则算法从大量的历史数据中挖掘出优质样本，然后利用优质样本建立BP神经网络模型，最后将与样本数据相似的历史数据和与样本数据出入较大的历史数据分别代入所建模型中，对雷达B的数据进行预测，检验所采用的方法是否满足实际要求。具体过程是：挖掘优质样本数据时，选择利用K-Means聚类分析算法对雷达A的左正和后正进行分类，将数值变量划分为类别变量，然后把雷达A相对雷达B测试的初速数据的误差进行标记：小于等于2‰标记为“好”，大于2‰标记为“差”，这样就将数值变量划分为文本分类变量。然后建立雷达A的左正和后正对应的类别与误差标记之间的关联规则，利用Apriori关联规则算法挖掘出误差标准为“好”的样本数据，这就是挖掘出的优质样本，聚类分析能够提升Apriori关联规则的挖掘质量[7]。随后利用挖掘出的优质样本数据建立BP神经网络模型，最后代入历史相似数据和历史出入较大数据对雷达B的初速进行预测。实验结果表明，利用挖掘出的优质样本数据建模预测时，与历史相似数据的预测值与实测值的平均相对误差基本上均小于1‰，达到了单台初速雷达测试弹丸炮口初速的误差标准，表明本文所建模型具有较高的预测精度；与历史出入较大的数据的预测值与实测值的平均相对误差虽然超过了1‰，但是预测值与实测值非常接近，相对误差全都接近0，表明本文所建模型具有一定的鲁棒性和泛化能力，最终表明由聚类分析关联规则神经网络构建的组合算法预测弹丸初速的方法是可行的。

1 聚类分析原理

聚类分析是指用某种方法将一系列对象分组，使分组后的对象相互关联、不同组的对象彼此区别的一类算法[8]。具体原理是根据数据自身的距离或相似度将它们划分为若干组，划分的原则是组内距离最小化而组间(外部)距离最大化。常用的聚类分析算法是K-Means算法，是典型的基于距离的非层次聚类算法，在最小化误差函数的基础上将数据划分为预定的类数K，把距离作为相似性的评价指标，数据对象距离越近，相似度就越大。

2 关联规则原理

关联规则最初提出的动机是针对购物篮分析问题提出的，即找出用户在一次购物时会同时购买哪些商品，以及同时购买这些商品的可能性有多大。用关联规则进行数据挖掘是指从数据背后发现事物之间可能存在的关联或者联系，挖掘出发生最频繁的数据集。Apriori算法是最具有影响力的挖掘频繁项集的经典算法之一，其思想是使用逐层迭代方式对数据库进行多次扫描，进而发现所有的频繁项集。第1次扫描得到频繁1-项集的集合L1，L表示对应的频繁项集合，第K(k>1)次扫描首先利用第(k-1)次扫描的结果Lk-1来产生候选集k-项集的集合Ck，然后在扫描过程中确定Ck的支持度，最后在每次扫描结束时计算频繁k-项集的集合Lk，然后由k阶频繁项集生成k+1阶候选项集，扫描事务集得到k+1阶频繁项集[9]，算法在候选集k-项集的集合Ck为空时结束。

支持度和置信度是衡量关联规则的两个重要指标，最小支持度表示项目集的最低重要性，最小置信度表示关联规则的最低可靠性，Apriori算法就是要挖掘出所有满足支持度阈值的频繁项集，然后在频繁项集上基于置信度对规则进行筛选[10]，当筛选出的规则的支持度和置信度分别大于支持度阈值和置信度阈值时，认为该关联规则是有效的，称为强关联规则[11]。

3 BP神经网络原理

BP神经网络模型[12]是人工神经网络模型[13]的一种，通常由一个输入层、若干个隐含层和一个输出层组成，各层均有一个或多个神经元节点，该模型利用误差逆传播算法，随着权值的不断训练，输出误差和目标输出误差的差值将逐渐减小，直到不再下降为止[14]。

研究表明，3层BP神经网络能够用相应的输入向量和输出向量逼近任何有理函数[15]，拓扑图如图1所示，n表示输入层输入向量的个数，h表示隐含层神经元的个数，m表示输出层输出向量的个数。正向传播和BP构成了BP神经网络的训练过程，在正向传播过程中，信号进入输入层并经过隐含层对其进行处理，最后在输出层输出训练结果，并对训练输出值进行比较得到信号误差；在BP过程中，信号误差则由输出层向输入层传播，通常可以调整各层链接权值和神经元阈值来减小信号误差；信号的正向传播和误差的BP是反复进行的，当网络输出误差小于设定误差或者迭代次数达到设定的学习次数时，训练过程结束，最后得到较理想的链接权值和神经元阈值[16]。

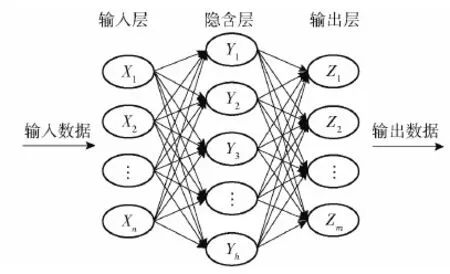
图1 3层BP神经网络拓扑图Fig.1 3-layer BP nurual network topology

4 组合算法挖掘过程

4.1 原始数据探索分析

图2 两台参试雷达现场布站示意图Fig.2 Site layout of two test radars

通常而言，将不同模型或者算法进行一定的组合，考虑问题将更系统、更全面，能最大限度挖掘出样本数据的信息，有效提高预测精度[17]。本文选择利用RStudio软件环境中的K-Means聚类算法和Apriori关联规则算法对历史数据进行数据分析、统计建模及数据可视化。在某型脱壳穿甲弹试验过程中，雷达A、雷达B与目标靶的位置关系如图2所示，从中可以看出发射的弹丸最先进入雷达B的电磁波照射范围，最后进入雷达A的电磁波照射范围，而且弹丸在雷达B的波束范围中飞行时间最长，雷达B测试的弹丸径向速度最完整，拟合递推出的初速数据相对更加准确，因此把雷达B测试的初速数据作为参照数据，并选取已测123发弹丸的初速建模分析。

雷达A布站的左正和后正分布情况如图3所示，之所以出现不同，是因为试验数据是不同日期开展的，而每次试验的参试人员不同，对雷达布站更多的是凭借自身经验，最后导致雷达A的左正和后正出现不同，这也是挖掘出两台雷达测速精度较为一致性的重要原因，左正和后正分别是雷达A天线面中心点相对战斗部炮管后方延伸线和耳轴的水平垂直距离(m)。

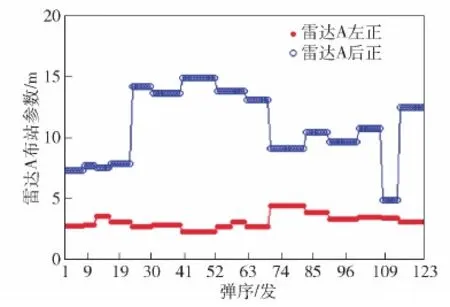
图3 雷达A左正和后正分布曲线Fig.3 Left positive and rear positive distribution curves of Radar A

图4 雷达A初速和雷达B初速变化曲线Fig.4 Variation curves of initial velocity of Radar A and Radar B

雷达A和雷达B的初速数据是两台雷达测试的同一发弹丸的初速数据(m/s)，分布曲线如图4所示。A对B的误差是指雷达A测试的弹丸初速与雷达B测试的弹丸初速的绝对误差，误差标准是雷达B测试的初速数据乘以2‰，123发弹丸的误差标准如图5所示。雷达A测试的准确性是指雷达A与雷达B初速绝对误差与误差标准的比较结果，小于等于误差标准时，准确性设置为好，大于误差标准时，准确性设置为差。

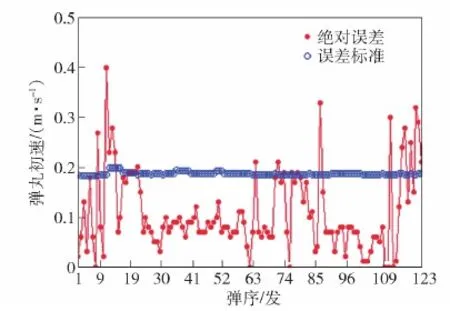
图5 绝对误差与误差标准变化曲线Fig.5 Absolute error and error standard variation curves

4.2 聚类算法进行分类

聚类分析是根据样本数据本身进行样本分组的一种方法[18]。先用K-Means聚类算法对雷达A的左正和后正两列数据进行分类，再结合两个参数的具体分布情况，初步判断其分布在4个区间。

选择手肘法对左正和后正进行分类，绘制不同类别数量下类内平方和变化曲线如图6所示，类间平方和变化曲线如图7所示，从中可以看出当聚类数k=4之后，类内平方和与类间平方和变化都趋于平缓，说明聚类数设为4较合适[19]。因此把左正和后正共同分为4类，分别为A1、A2、A3和A4。

图6 不同类别数量下类内平方和变化曲线Fig.6 Variation curve of sum of squares within groups under different numbers of categories

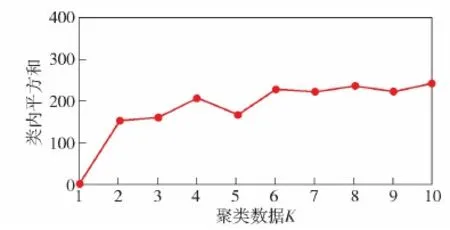
图7 不同类别数量下类间平方和变化曲线Fig.7 Variation curve of sum of squares between groups under different numbers of categories

绘制第1～123发弹丸中雷达A的左正、后正对应的分类类别如图8所示，10～20之间代表A1类，20～30之间代表A2类，30～40之间代表A3类，40～50之间代表A4类，可以看出A2类和A4类在样本数据中的占比最重。

图8 分类类别示意图Fig.8 Schematic diagram of classification category

4.3 关联规则挖掘分析

因为关联规则能够筛选出主要因素候选集[20]，所以把聚类算法划分出的类别作为关联规则的左规则，雷达A初速的准确性作为关联规则的右规则，利用Apriori关联规则算法挖掘出频繁项集，为挖掘出尽可能多的频繁项集，把支持度阈值设为0.26，置信度阈值设为0.86，运行算法最后挖掘出2条关联规则如表1[21]所示。

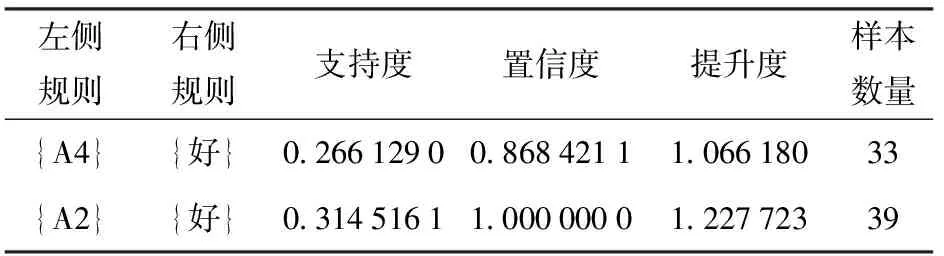
表1 Apriori关联规则算法挖掘结果Table 1 Results of Apriori algorithm for association rule mining

关联规则{A4}=>{好}的含义是雷达A的左正处于区间3.3～4.4、后正处于区间9.1～10.8时测速准确性均为好；关联规则{A2}=>{好}的含义是雷达A的左正处于区间2.3～3.1、后正处于区间13.7～14.9时测速准确性均为好，而且这两个关联规则的提升度均大于1，属于强关联规则[22]。结合试验实际情况也可以理解，雷达射角与火炮射角是一致的，雷达发射的电磁波呈圆锥形而且波束有一定宽度，当火炮射角很大时，要保证弹丸一出炮口就进入雷达波束范围内，雷达就必须近距离放置在火炮侧后方，此时后正就小，就需要采用关联规则{A4}=>{好}进行布站；当火炮射角不是很大时，要保证弹丸一出炮口就进入雷达波束范围内，雷达就必须远距离放置在火炮的侧后方，此时后正就大，就需要采用关联规则{A2}=>{好}进行布站。

绘制123发弹丸中所有类别和测速准确性构成的关联规则的频率分布如图9所示，从中可以看出关联规则{A2}=>{好}和{A4} =>{好}分布数量是最多的，也反过来证明了所挖掘出的两个关联规则的确是最频繁的项集，表明挖掘结果是正确的。

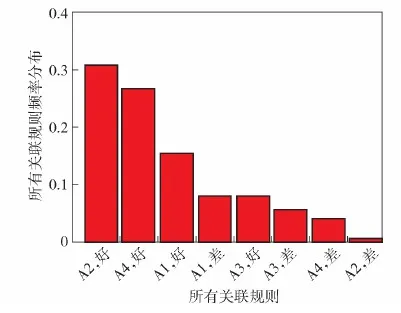
图9 表1所有关联规则频率分布Fig.9 Frequency distribution of all association rules inTable 1

5 实验验证

为证明挖掘出的样本数据是优质样本，有利于提升预测弹丸初速的准确性，本文实验验证选择利用RStudio软件环境进行样本数据分析、对样本数据进行统计并建立BP神经网络模型，以及对预测结果进行可视化分析。

5.1 预测模型的设计与实现

由于神经网络模型属于非线性映射模型，能够提取输入数据的特征信息，挖掘出更深层次的潜在规律[23]，选择利用样本数据建立BP神经网络模型预测分析。为能够训练出稳定可靠的神经网络模型，选择按照A4规则在前、A2规则在后的顺序把两个样本数据整合到一起，增加训练样本的数量以构成组合样本，组合样本的数据共有72行。

建模前，为检验挖掘出的组合样本中雷达A的左正、后正和初速与雷达B初速之间的相关性，以及雷达A的左正、后正和初速是否有利于提升预测雷达B初速的准确性，选择计算组合样本的相关系数并绘制相关系数矩阵如图10所示。图10右侧色标尺表示相关系数，向上颜色越深，正相关系数越大，正相关性也越强；向下颜色越深；负相关系数越大，负相关性也越强；颜色越浅，相关系数越接近零，相关性越弱。由图10可知，组合样本中雷达A的左正、后正和初速与雷达B初速之间的相关系数均不为0，是存在相关性的，具有一定的因果关系，因此雷达A的数据有利于提升预测雷达B数据的精度。

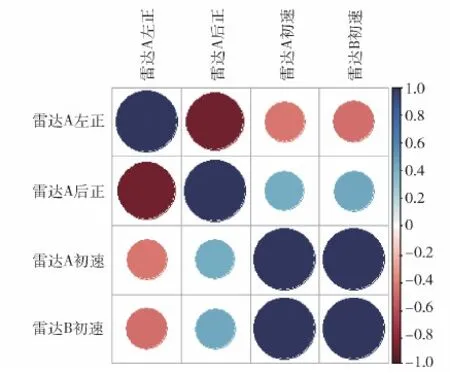
图10 组合样本中雷达A的左正、后正和初速与雷达B 初速之间的相关系数矩阵可视图Fig.10 Visibility graph of correlation coefficient between left positive, back positive, initial velocity of Radar A and initial velocity of Radar B in combined samples

在对组合样本进行建模时，选择采用3层BP神经网络架构实现雷达A的输入向量到雷达B的输出向量的非线性映射，同时由于隐含层神经元的个数太多，导致模型的计算复杂性提升，隐含层神经元的个数太少又导致模型对原始信息提取能力的不足[24]，因此确定模型的输入向量n=3，输出向量m=1，隐含层神经元的个数h=6，同时把学习效率设为0.01，误差上限设为0.001，最大迭代次数设为2 000，最后组合样本训练的BP神经网络经过590次迭代算法即结束。

随着迭代次数的增加，残差平方和变化曲线如图11所示，输入层到隐含层的权值向量和阈值如表2所示，隐含层到输出层的权值向量如表3所示。最后得到BP神经网络对组合样本中雷达B测试的弹丸初速预测值与组合样本中雷达B测试的弹丸初速实测值关系曲线如图12所示，可见BP神经网络对组合样本的预测值与其实测值是比较吻合的[25]，至此，根据组合样本建立的BP神经网络模型就训练好了。所建模型应该具备两个能力，输入与历史数据相似的数据时，能够得到准确的输出，鉴于BP神经网络具有较好的鲁棒性，当输入与历史数据出入较大的数据时，模型也能给出相对准确的输出。下面围绕这两方面的能力进行分析验证。

为起到侧面对比的作用，选择引入支持向量回归机(SVR)作为对比模型，由于高斯核函数具有良好的学习性能和较宽的收敛阈，把高斯核函数作为SVR的核函数[26]。

图11 组合样本神经网络残差平方和随迭代次数变化曲线Fig.11 Variation curve of the residual sum of squares of combined sample neural network with the number of iterations

表2 组合样本神经网络输入层到隐含层权值 和阈值Table 2 Weights and thresholds from input layer to hidden layer of combined sample neural network

表3 组合样本神经网络隐含层到输出层权值Table 3 Weights from hidden layer to output layer of combined sample neural network

图12 BP神经网络对组合样本中雷达B测试的 弹丸初速预测值Fig.12 Prediction value of projectile muzzle velocity measured by radar B in combined samples by BP neural network

5.2 利用与历史相似数据建模分析

1)对A1规则进行预测

选择原始数据中第1～5行作为测试数据，把测试数据代入所建模型中就得到预测值与实测值如表4所示，BP神经网络预测值与实测值的平均相对误差为0.083%，小于1‰，而SVR预测值与实测值的平均相对误差为2.16%。

2)对A2规则进行预测

通过对语言政策与社会发展互动关系的研究，可以提取制约语言文字政策定位的因素，为国家语言政策和规划的制定提供理论支撑。

选择组合样本中A2规则的最后5行即原始数据第58～62行作为测试数据，最后预测出雷达B的初速数据与实测值如表5所示，BP神经网络预测值与实测值的平均相对误差为0.088%，小于1‰，而SVR预测值与实测值平均相对误差为0.097%。

3)对A3规则进行预测

选择原始数据中第66～70行数据作为测试数据，得到预测值与实测值如表6所示，BP神经网络预测值与实测值的平均相对误差为0.019%，小于1‰，SVR预测值与实测值平均相对误差为0.225%。

4)对A4规则进行预测

选择组合样本中A4规则的最后5行即原始数据第104～108行作为测试数据，得到预测值与实测值如表7所示，BP神经网络预测值与实测值的平均相对误差为0.083%，小于1‰，SVR预测值与实测值平均相对误差为0.113%。

对A1规则、A2规则、A3规则和A4规则的预测结果表明，相比SVR，利用组合样本建立好的BP神经网络模型在对与历史相似数据进行预测时精度最高，所建模型预测误差均小于1‰，达到了单台初速雷达测试弹丸初速误差小于1‰的要求，验证结果通过了检验(见表4～表7)。

表4 雷达B第1～5发实测值与神经网络预测值Table 4 Measured values and neural network predicted values of the 1st ～ 5th rounds of Radar B

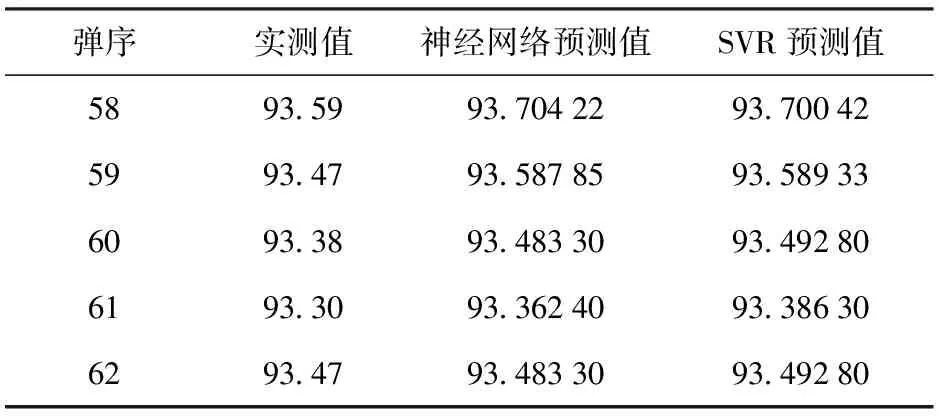
表5 雷达B第58～62发实测值与神经网络 预测值Table 5 Measured values and neural network predicted values of the 58th ～ 62nd rounds of Radar B

表6 雷达B第66～70发实测值与神经网络 预测值Table 6 Measured values and neural network predicted values of the 66th～70th rounds of Radar B

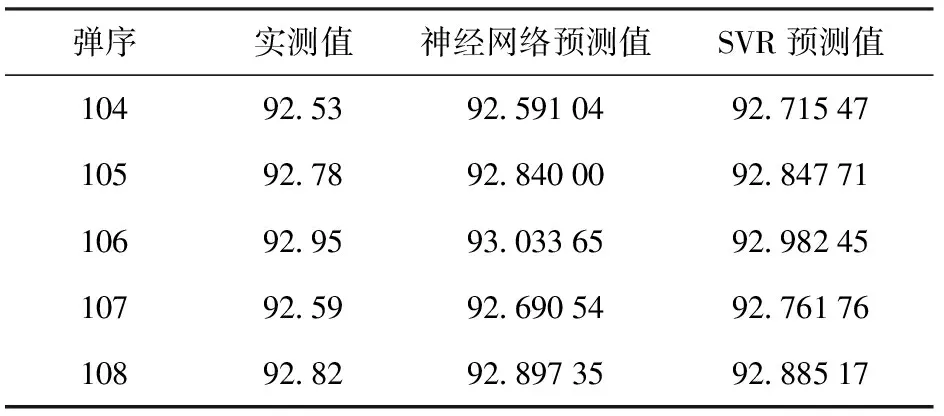
表7 雷达B第104～108发实测值与神经网络 预测值Table 7 Measured values and neural network predicted values of the 104th～108th rounds of Radar B

5.3 利用与历史出入较大数据建模分析

选择某型坦克炮试验中两台初速雷达测试的另一弹种初速数据进行验证，两组弹丸初速分别记为v1和v2。v1中雷达A的左正为1.5 m，后正为14.8 m，雷达A的初速与雷达B的初速变化曲线如图13所示，雷达A的数据与历史数据有很大不同。v2中雷达A的左正为1.9 m，后正为15.7 m，雷达A初速和雷达B初速变化曲线如图14所示，可见雷达A的数据与历史数据有很大不同。把雷达A的数据代入所建模型中，就能预测出雷达B的初速，v1中雷达B实测值与预测值如表8所示，v2中雷达B实测值与预测值如表9所示。

图13 v1雷达A与雷达B初速变化曲线Fig.13 Initial velocity variation curve of v1 Radar A and Radar B

图14 v2雷达A与雷达B初速变化曲线Fig.14 Initial velocity variation curve of v2 Radar A and Radar B

经过计算，得到v1中BP神经网络预测值与实测值的平均相对误差为0.380%，SVR预测值与实测值的平均相对误差为11.04%；v2中BP神经网络预测值与实测值的平均相对误差为0.616%，SVR预测值与实测值的平均相对误差为10.39%。由此可以看出，v1和v2中BP神经网络模型预测值精度高于SVR，虽然神经网络预测值与实测值的误差均超过了1‰，但是预测值已经非常接近实测值了，v1神经网络预测值与实测值的相对误差分别为0.004 188 980、 0.005 472 066、0.003 095 210、0.003 339 775、0.002 913 593，v2神经网络预测值与实测值的相对误差分别为0.005 701 651、0.006 389 111、0.005 933 035、0.006 386 048、0.006 389 111，全部都非常接近0，说明预测值与实测值的偏差非常小，综合表明神经网络预测结果是准确有效的[27]。

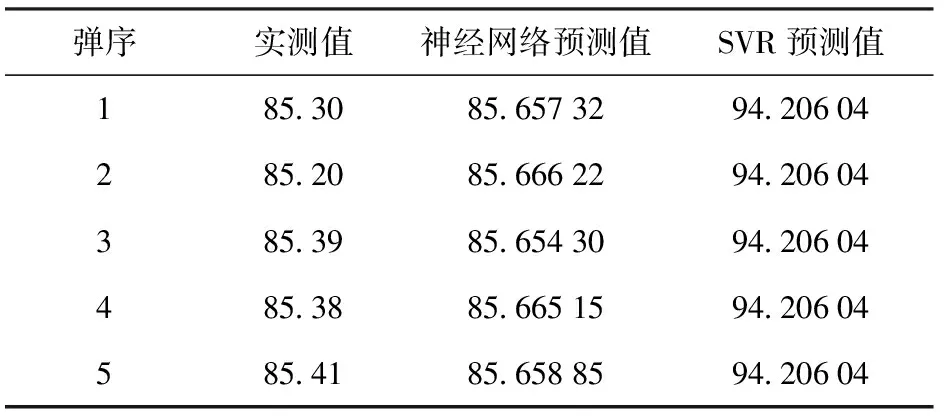
表8 v1雷达B实测值与BP神经网络预测值Table 8 Measured values of v1 Radar B and predicted values of BP neural network

表9 v2雷达B实测值与BP神经网络预测值Table 9 Measured values of v2 Radar B and predicted values of BP neural network

综上所述，利用挖掘出的组合样本建立的BP神经网络模型对与历史相似数据进行建模预测时，预测误差达到了单台初速雷达测试弹丸初速误差小于1‰的要求，对与历史出入较大的数据进行建模预测时，虽然预测误差超过了1‰，但是预测值已经非常接近实测值，预测值与实测值的相对误差基本为0，而且预测精度始终高于SVR。证明了组合样本建立的BP神经网络模型既保证了预测精度，又具有一定的鲁棒性和泛化能力，而这主要得益于聚类分析和关联规则挖掘出的优质样本数据，以及所建BP神经网络的鲁棒性和容错能力。也可以看出，虽然SVR同样拥有较强的非线性映射能力，但是同样的核函数下其预测精度并不稳定，尤其输入与历史数据偏差较大的数据时误差会明显增大，往往需要测试多种核函数和参数组合才能找到效果较优的模型，但是通常很难找到一个合适的核函数，而且在样本数据较大时，其训练速度会变慢[18]。

实际上，预测弹丸初速时样本量越多，包含的规律和特征才能更全面，模型预测精度才会更高，但是样本量越多，重构值和异常值也会越多，SVR对重构值非常敏感，此时聚类分析、关联规则与BP神经网络构成的组合算法就能充分发挥出其重要作用，下一步需要研究能否利用其他模型代替BP神经网络以进一步提高预测精度。

6 结论

本文针对靶场试验中，某台初速雷达测试的弹丸初速有时出现重构或不准确的情况，把共同参试的两台雷达测试的初速数据进行融合，然后利用聚类分析和关联规则从大量历史试验数据中挖掘出两台雷达测试初速误差小于2‰的样本数据，最后利用挖掘出的优质样本数据建立BP神经网络模型预测出重构的或不准确的数据。得出以下主要结论：

1)由聚类分析、关联规则和BP神经网络建立的组合算法可以作为弹丸初速的预测模型，尤其在数据量非常大的情况下更能发挥出重要作用。

2)把雷达的后正、左正和误差标准对应起来，利用聚类关联规则组合算法挖掘优质样本的数量还不够充分，损失了很多其余优质样本，下一步考虑如何更充分地挖掘出所有优质样本数据。

3)BP神经网络模型适用于海量的样本数据，当样本数据较少时，可以考虑利用SVR建模预测，并检验其预测精度高低。

4)靶场试验中，有的雷达测试弹丸的径向速度，有的测试弹道坐标，有的测试弹丸飞行角度，其中都会出现需要数据重构的情况，可以考虑引入文章所提方法，或者探究出更为理想的预测方法。