高速履带车辆机电悬架惯量分析与滤振缓冲设计
2023-03-21宋慧新顾亮张进秋董明明王利明
宋慧新, 顾亮, 张进秋, 董明明, 王利明
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.中国北方车辆研究所 底盘部件技术部, 北京 100072;3.陆军装甲兵学院 车辆工程系, 北京 100072; 4.重庆大学 机械传动国家重点实验室, 重庆 400044)
0 引言
机电悬架研究始于20世纪90年代[1],最初用于军用车辆,在20世纪初完成了试验验证,主要代表是德克萨斯大学研制的机电悬架系统,采用的执行器分别为齿轮齿条与电机组合的直线式执行器、液压缸串联液压马达与电机的直线式执行器、行星减振器与电机串联的旋转式执行器,分别在高机动多用途轮式车(HMMWV)[2]、中型战术车(LMTV)[3]、枪骑兵履带车(Lancer)上完成原理样机道路试验[4]。
如何快速衰减甚至回收振动能量是高机动履带车辆行驶系统发展的一个重要方向[5]。Hamid[6]研究指出:机电悬架回收能量的最大影响为电机的线圈内阻、悬架阻尼系数、负载电阻和土壤轮胎等效刚度。寇发荣等[7]设计了一种电磁复合式馈能悬架结构,提出由主环与内环构成的半主动控制策略,使电机回馈能量的72.5%储存至超级电容。Zhao等[8]针对执行器等效惯性质量过大的问题,提出了一种新的主动悬架双减振结构,采用逐步改变充电电压的方法将振动能量直接回收到电池组中。
喻凡等[9]、黄昆等[10]、殷珺等[11]、曹民等[12]提出了由滚珠丝杠结合直流无刷电机构成的机电悬架作动器方案,可以将车辆乘适性提高30%,可以回收路面振动能量并将车辆乘适性提高10%[10]。张进秋等[13-14]、王兴野等[15]、彭虎等[16]提出了由齿轮齿条结合直流无刷电机构成的机电悬架作动器方案,研究表明惯性质量对于悬架低频的特性有利,但不利于车辆在高频时的平顺性,且会带来冲击问题[15];提出的悬架多模式切换控制器有效平衡了减振及馈能之间的矛盾关系[16];提出的有限频域H∞控制算法有效地降低了时滞对控制的影响,提高了车辆在4~8 Hz频域范围内的乘适性[14]。汪若尘等提出了基于直线电机的机电悬架[17],并提出了一种混合机电悬架,能够有效改善悬架动力学性能,明显减少能量消耗[18]。王庆年等[19]对滚珠丝杠式机电悬架,以提高馈能效率为目标,从结构和效率两方面对丝杠参数进行了匹配和校核,能够高效地回收悬架振动能量。
但是机电悬架在可靠性、稳定性、失效保护和成本等方面仍然有很多问题需要解决。由于高速履带车辆对悬架空间约束要求较严、对悬架减振性能要求较高,高速履带车辆机电悬架一般应用了传动装置、马达或旋转电机等部件,以求获得更小的体积和更好的减振性能。旋转电机的能量利用与回收的效率高,并且结构紧凑,但过大的路面冲击极易造成传动机构的损坏,加之传动机构的保养维护比较困难,整个系统的寿命会大幅缩短[13]。旋转电机式馈能悬架由于传动装置的固定连接方式以及较大的转动惯量,恶劣路面的冲击和频繁地转向会导致传动装置和电机极易损坏,因此可靠性差[13]。
在悬架垂向往复的运动过程中,旋转部件产生惯性力,如果旋转加速度过大,则会产生过大的冲击力矩,对传动装置、连接轴等强度较弱的零部件造成损坏;另一方面,这部分冲击力矩会对悬架性能产生非常不利的影响。因此如何尽可能减小惯性力的不利影响,成为机电悬架首先要解决的问题。利用电机产生主动力矩,可以补偿和改变转动惯量带来的不利影响。这是通过控制电机解决惯量问题的方法,该方法对采集精度、控制时滞、电机响应等要求高,因此难度大。为降低惯量影响,设计时要优化匹配传动装置和电机性能、尽可能降低传动比、降低旋转部件转动惯量。
本文分析了高速履带车辆旋转式机电执行器的构成、悬架特性,研究了惯性质量对机电悬架性能的不利影响,得到了不同等级路面随机振动输入时惯性质量在频域和时域对簧载质量加速度、悬架动挠度、负重轮相对动载荷、惯性力等影响;计算了随机路面输入下惯性力的谱密度,提出滤振缓冲的解决措施。对滤振缓冲对于缓解惯性质量不利影响的效果进行了模拟仿真。通过仿真和试验,验证了滤振与缓冲的措施能够提升机电悬架的性能,有助于解决惯性质量带来的不利影响。
1 2自由度悬架模型
1.1 机电悬架原理
本文的机电悬架应用扭杆弹簧作为弹性元件,应用机电执行器为阻尼元件。机电悬架馈能状态下能量耗散或回收的原理如图1所示。图1中,Dr、Dp为开关管,R为电阻,Cr为耗散模式控制线,Cp为吸能模式控制线,ua、ub、uc为电机的三相线,T为摇臂的扭矩。
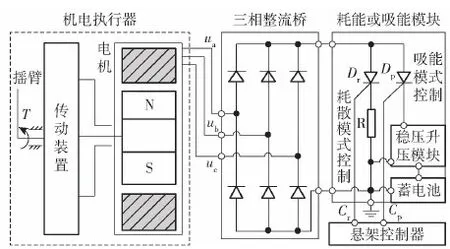
图1 机电悬架能量耗散或回收原理Fig.1 Energy dissipation or recovery principle of electromechanical suspension
机电执行器的摇臂带动传动装置,传动装置将摇臂的运动放大后传递到电机,使电机转子旋转,从而使电机定子线圈输出三相交流电压。电压经三相整流桥整流输出直流电压。悬架控制器能够实现两种控制模式:在耗散模式下,悬架控制器控制开关管Dr,从而调节电阻R的耗电功率,形成阻碍摇臂旋转的电磁力;在吸能模式下,悬架控制器控制开关管Dp,从而调节电能的回收能力,形成阻碍摇臂旋转的电磁力。
1.2 悬架的构成与刚度变化特性
本文研究高速履带车辆大惯量机电悬架,其参数如表1所示,其单轮总成如图2所示。图2中,A为平衡肘旋转点,B为负重轮中心,C为连杆与机电执行器摇臂的铰接点,D为机电执行器摇臂的旋转点,E为连杆与平衡肘的铰接点,Rd为平衡肘的旋转关径,ms为簧载质量,α为平衡肘与水平线的夹角,αd为动行程角,αj为悬架静态下平衡肘与水平面之间的静倾角,zr为路面输入的垂向位移,zu为负重轮垂向位移,以悬架静平衡时负重轮中心为原点,zs为簧载质量垂向位移,以悬架静平衡时簧载质量重心为原点,Ff为扭杆在负重轮轴上的垂直弹性力,δ为负重轮与履带的变形量。

表1 悬架参数Table 1 Suspension parameters
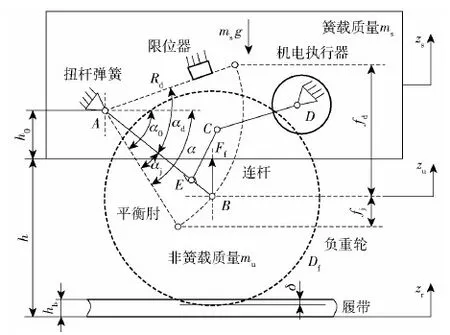
图2 单轮机电悬架总成与运动关系Fig.2 Single wheel’s electromechanical suspension assembly and motion relationship
由图2可知,该悬架由平衡肘、扭杆弹簧、限位器、机电执行器、连杆组成。悬架的扭杆、机电执行器、限位器固定在簧载质量上,平衡肘通过旋转副与负重轮连接,负重轮压接在履带上。扭杆为弹性部件、机电执行器为阻尼部件。
假设平衡肘初始安装角α0对应悬架变形位移零点。则通过对模型运动分析可知,悬架相对位移fx与平衡肘的安装角α0有如下关系:
fx=Rdsinα-Rdsinα0=zu-zs
(1)
式中:由式(1)可得到平衡肘与水平面的夹角α的变化关系如式(2)所示:
α=arcsin [(zu-zs)/Rd+sinα0]
(2)
Ff可表示
Ff=(GJ/l)×(α-α0)/(Rdcosα)
(3)
扭杆的极惯性矩J计算为
(4)
扭杆悬架刚度的计算如式(5)所示:
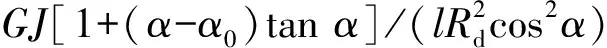
(5)
αj如式(6)所示:
αj=arcsin (Df/2+hb-h-h0-δ)/Rd
(6)
式中:
δ=(ms+mu)g/kl+(ms+mu-ml)g/kf
(7)
ku=kfkl/(kl+kf)
(8)
g为重力加速度。
根据式(1)~式(5),可计算出悬架的刚度变化如图3所示。
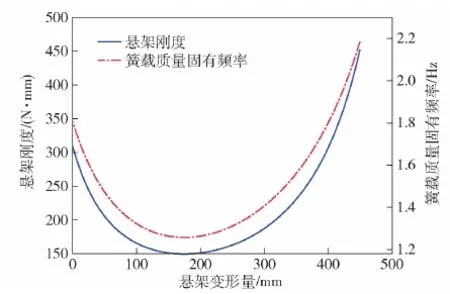
图3 悬架变形量与悬架刚度、簧载质量固有频率关系Fig.3 Relationship between suspension deformation and suspension stiffness/sprung mass natural frequency
由悬架相对位移与悬架刚度对应关系可知,刚度呈明显的非线性特性,悬架在平衡位置刚度基本最小,有利于发挥缓冲性能,在上升段刚度明显增大,有利于实现更大储能,防止撞击上限位;在下降段,刚度明显增大,不利于压缩和缓冲。得到刚度变化,即可得簧载质量固有频率fs0的变化(见图3)。固有频率的变化范围为1.27~2.00 Hz,为分析当固有频率变化时惯性质量对悬架特性的影响提供了数据支撑。
1.3 复杂连杆运动关系的求解
为计算准确的惯性质量,需要得到执行器旋转角度与悬架动挠度之间的变换关系,为此需要确定连杆运动关系。由于执行器通过连杆机构与平衡肘相连接,悬架变形量与摇臂旋转角度对应关系较复杂。为简化模型,同时保证模型的精度,分析杆系运动关系如图4所示,悬架杆系参数见表2,计算在全行程内悬架变形量与摇臂旋转角度的对应关系。图4中,τ为AD与水平线夹角,βd为CD与水平线夹角,ψ为AD与CD夹角,φ为CD与DB夹角,θ为CE与EB夹角,γd为AB与BD夹角,F为垂足。
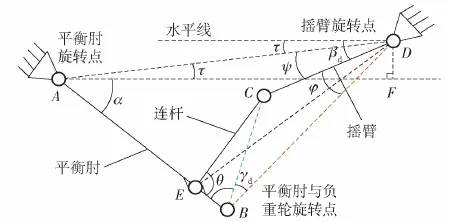
图4 机电悬架系统杆系运动关系分析图Fig.4 Analysis of linkage motion relationship for the electromechanical suspension system

表2 悬架杆系参数Table 2 Suspension linkage parameters
段国柱等[20]通过对连杆系的运动学分析得出连杆系的运动学特性,为连杆机构的设计和机电悬架的力学特性分析提供了依据。本文对杆系变化的各种情况进行分析,利用三角函数计算得到悬架动挠度fx与摇臂角度βd的对应关系图,如图5所示。从图5中可以看出,当负重轮的位移在0~428 mm时,悬架相对位移与摇臂角度的关系基本为线性对应关系,通过线性拟合得到悬架相对位移与摇臂角度的关系直线方程如式(9)所示,直线形状如图5所示。
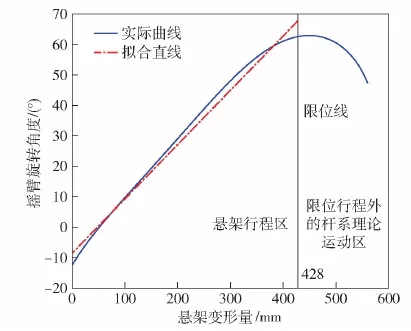
图5 悬架变形量与摇臂旋转角度对应关系与拟合直线Fig.5 Relationship between suspension deformation and rocker arm rotation angle as well as the fitted straight line βd=0.178 4fx-8.550 8
(9)
1.4 惯性质量的等效计算
本文研究的机电悬架执行器结构原理如图6所示,摇臂将振动依次通过行星传动装置的外齿圈、外行星轮、内行星轮、太阳轮传递给电机转子,实现振动幅值与速度的放大。
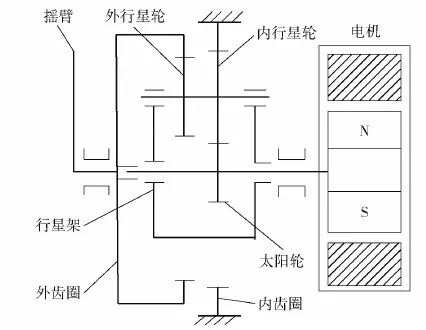
图6 执行器内部结构原理Fig.6 Internal structure principle of actuator
惯性质量mr是指在机电悬架执行器中将悬架运动转换为电机旋转运动中所涉及的部件转动惯性在悬架上的等效值,即将摇臂、传动装置、电机转子转动惯量、等效到悬架上的质量。机电执行器采用两级传动,摇臂与外齿圈的转动惯量为Jr,其变速比ir为1;行星架与行星轮组总成的转动惯量为Jx,变速比为ix;带太阳轮轴的电机轴总成的转动惯量为Jd,变速比为id。机电执行器参数如表3所示。

表3 机电执行器参数Table 3 Parameters of electromechanical actuator
假设βs是悬架动挠度与机电执行器旋转角度βd的比例系数,
(10)
由式(9)可知,βs=3.112 rad/m。可得惯性质量为
(11)
通过式(11),经计算,mr=526 kg。
1.5 简化的2自由度模型
为得到一般性的规律,以静平衡位置对应的悬架刚度为模型的悬架刚度。建立2自由度悬架模型如图7所示,假设条件为:1)悬架的刚度系数、阻尼系数、负重轮的刚度系数、负重轮的阻尼系数为常值;2)不发生撞击限位器的情况;3)忽略摩擦力。根据模型示意图,建立方程,如式(12)、式(13)所示。图7中,cs为悬架阻尼系数,cu为负重轮阻尼系数,ks为悬架刚度,ku为负重轮与履带串联刚度,mr为惯性质量。
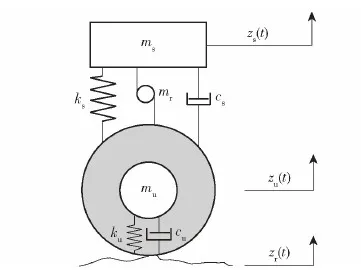
图7 2自由度机电悬架模型Fig.7 Two-degree-of-freedom (2DOF) electromechanical suspension model
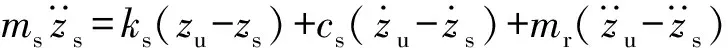
(12)
(13)
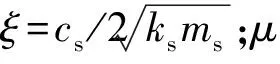
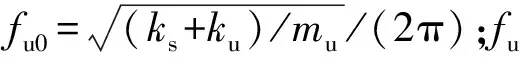
λ为频率比,f为路面输入的激振频率,λ=f/fs0。
通过式(12)、式(13)进行傅立叶变换,得到簧载质量加速度、负重轮的相对动载荷Fd/Gs(其中Fd为动载荷,Gs为静载荷)、悬架动挠度fd相对路面输入速度的传递函数,如式(14)、式(15)、式(16)所示。
(14)
(15)
(16)
式中:
X=(1-4εξ2λ2/γ-μβλ2)2+(2ξλ+2εξλ/γ-2λ3μβεξ/γ)2
Δ=(γ-λ2-γλ2-μλ2+μλ4+μβλ4-4εξ2λ2+μ2βλ4-γμβλ2)2+(2εξλ-2μξλ3-2ξλ3+2γξλ-2εξλ3-2μβεξλ3)2
F=[1+γλ2-γ+μλ2+μλ4-μβλ2-μβλ4+4εξ2λ2-μ2βλ4-(4εξ2λ2/γ)+μγβλ2]2+4(ξλ+ξλ3+μξλ3-εξλ-γξλ+εξλ3+εξλ/γ-εξλ3/γ+μεβξλ3-μεβξλ3/γ)2
惯性冲击力Fr关系到机电悬架部件设计的强度可靠性,Fr相对路面输入位移的频响函数可表示为
(17)
2自由度机电悬架模型参数见表4,将数据代入fs和fu的计算公式,计算可见惯性质量使簧载质量与非簧载质量的固有频率均减小。

表4 2自由度悬架模型参数Table 4 Parameters of 2DOF electromechanical actuator
2 惯性质量带来的不利影响
2.1 频域下惯性力与悬架特性的计算
根据不同路面随机输入的模型[21],不同路面不平度系数、参考空间频率、车速确定后,由式(17)可求得惯性质量惯性力的均方根值为
(18)
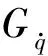
同理,可求得不同路面等级时,簧载质量加速度、相对动载荷、悬架动挠度的均方根值计算公式为
(19)
(20)
(21)
用离散积分的方法代替连续积分,从而简化计算,其中频率取0.1~100 Hz,计算不同路面等级下惯性力的均方根值。车速从0~120 km/h变化,可求得D级路面时惯性力均方根值随车速的变化,以及D级路面时有无惯性质量时的簧载质量加速度均方根值随车速的变化(见图8)。

图8 惯性力与簧载质量加速度随车速的变化Fig.8 Variations of inertia force and sprung mass acceleration with vehicle speed
从图8中可知:随着车速的增大,惯性力的均方根值增大,从而使悬架平顺性恶化,同时影响悬架部件的可靠性,这是机电悬架要解决的首要问题;随着车速的增大,簧载质量加速度的均方根值相对无惯性质量的悬架显著增大,同时惯性质量越大,则簧载质量加速度的均方根值越大。因此惯性质量对簧载质量加速度有很大影响,应尽可能减小机电悬架的惯性质量。
通过式(18)、式(19)、式(20)、式(21)的计算,即可计算全频谱时、有无惯性质量时各级路面悬架指标的均方根值,以便进行对比。例如得到D级路面、行驶速度为40 km/h的悬架惯性力均方根值、悬架特性指标均方根值的对比,如表5所示。

表5 频域内D级路面车速40 km/h时悬架 特性对比Table 5 Comparison of suspension characteristics at 40 km/h on class F road in the frequency domain
由表5可见:随着惯性质量的增大,惯性力的均方根值显著增大,簧载质量加速度均方根值显著增大;相对动载荷变化较小,尤其是悬架动挠度的影响很小。
2.2 时域下惯性力与悬架特性的功率谱密度分布
为进一步分析惯性质量造成的不利影响,以不同等级的路面输入,作为2自由度悬架模型的激励,计算时域下惯性质量的惯性力、簧载质量加速度、相对动载荷、悬架动挠度的均方根值。以D级路面行驶速度为40 km/h为例,仿真时长20 s,得到簧载质量加速度的功率谱密度如图9所示,惯性质量为526 kg的悬架相对惯性质量为0 kg的悬架,其簧载质量加速度对比发生变化的转折频率点定义为转折频率fz。
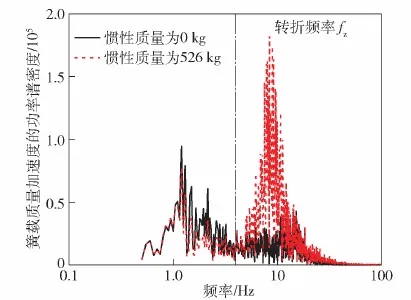
图9 不同惯性质量时簧载质量加速度的功率谱密度Fig.9 Power spectral density of sprung mass acceleration with different inertial masses
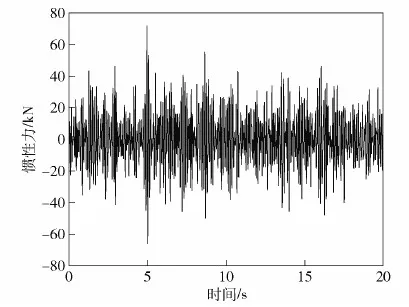
图10 D级路面车速40 km/h时惯性力Fig.10 Inertia force at 40 km/h on Class D road
从图9中可知,在转折频率fz(图9中为4.32 Hz)的左侧,惯性质量为526 kg的悬架簧载质量加速度值小于无惯性质量的悬架,但在转折fz的右侧,惯性质量为526 kg的悬架簧载质量加速度值远大于无惯性质量的悬架。图10为D级路面车速40 kg/h时的惯性力。
由图10可见,惯性力随路面输入变化,峰值较多,可求得其中最大值为71 841 N(对应最大扭矩为25 863 N·m)。对惯性力进行功率谱密度分析,结果如图11所示。图11中,滤振高频fg=17.78 Hz。由图11可见,惯性质量为526 kg时,惯性力的功率谱密度在第二主频附近(4.32~17.78 Hz),功率谱密度值较大,表明惯性质量造成第二主频区振动剧烈。因此为解决惯性质量的冲击问题,应消减第二主频附近的惯性力。
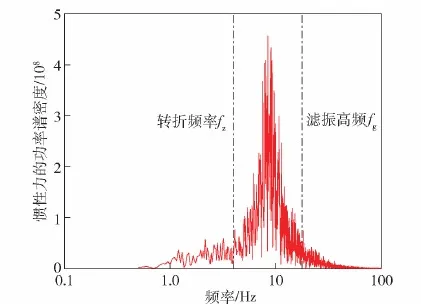
图11 惯性质量为526 kg时惯性力的功率谱密度Fig.11 Power spectral density of inertial force under the inertial mass of 526 kg
3 滤振与缓冲措施
3.1 滤振措施
研究表明:第一主频共振频点右侧至第二主频共振频点左侧之间的频段,以及第二主频共振频点右侧至无穷大频段,阻尼越小,悬架平顺性越好[22]。另一方面,考虑到高频共振频点附近悬架动挠度的振动幅值较小,因此采用对转折频率fz至无穷大频段幅值滤振的方法,以滤除此频段过大的惯性力,如图12所示。
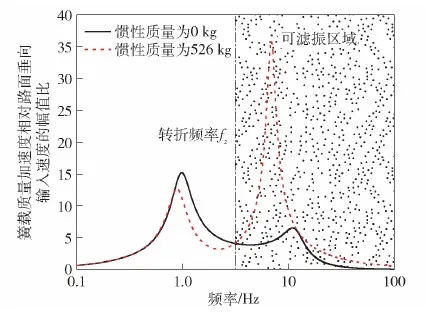
图12 滤振起始频率与滤振区域的图示Fig.12 Diagram of the initial frequency of vibration filtering and the vibration filtering region
3.1.1 滤振起始频率的计算与变化范围
将转折频率fz作为滤振起始频率,该频率为带有惯性质量的机电悬架与相同参数的无惯性质量的悬架在幅频特性曲线中第一主频右侧相交的点所对应的频率,如图12所示。
根据式(16),不同惯性质量比(β1=0、β2=2.24)的幅值相等,则有
(22)
由式(22)可知,若使左右相等,有且只有
Δ(β1)=Δ(β2)
(23)
根据图12与式(23),可计算得到滤振起始频率为4.32 Hz。对于确定的悬架系统而言,惯性质量比是确定的。因此影响起始频率的参数主要有质量比,即簧载质量的变化对起始频率产生影响。高速履带车辆的簧载质量会在空满载的情况下产生变化,假定其在2 000~3 000 kg之间变化,得到起始频率变化如图13所示。
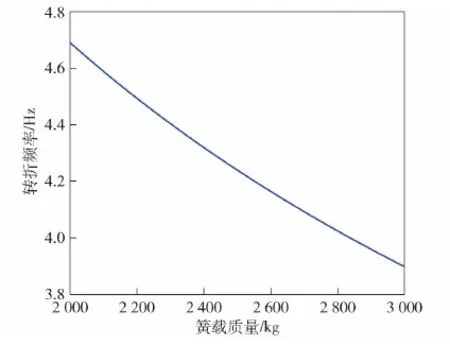
图13 滤振起始频率随簧载质量变化关系Fig.13 Variation of the initial frequency of vibration filtering with sprung mass
因此可知,簧载质量为2 000 kg时,对应起始频率为4.69 Hz;簧载质量增大,则起始频度降低;当簧载质量为3 000 kg时,对应起始频率为3.90 Hz;因此簧载质量在合理范围内变化对起始频率影响不大。
3.1.2 滤振幅值的计算
合理地设计滤振幅值的目的是有效地减小惯性力对于机电悬架的恶劣影响,同时有利于提升平顺性。
滤振幅值e与车速、路面等级以及需要滤除的频率范围是相关。为更精确地确定滤振的频率范围,根据图13所示,选取滤振的频率范围为 4.32~17.78 Hz。根据式(21)即可计算出不同等级随机路面下,不同行驶速度时悬架动挠度的均方根值。行驶速度越高、路面越差,则悬架动挠度均方根值越大。为了更好地滤除惯性力,根据车辆行驶速度的要求,即可确定滤振幅值。例如,要求车辆在C级路面最大行驶速度为100 km/h,可知对应的动挠度均方根值为7 mm。确定好滤振幅值后,可以根据滤振幅值,确定在各级路面行驶时悬架动挠度均方根值所对应的行驶速度,如表6所示。
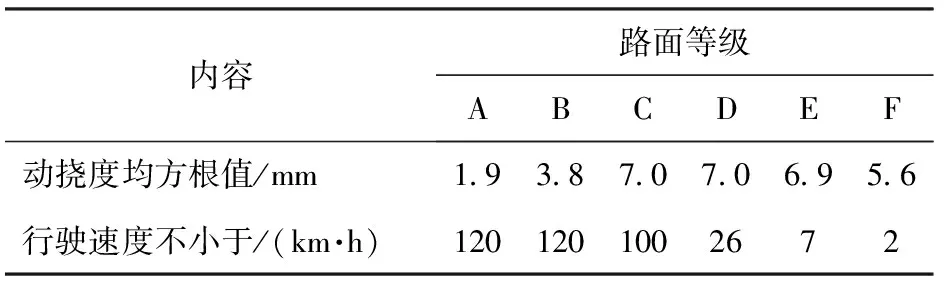
表6 滤振幅值7 mm以下对应的不同路面 行驶速度Table 6 Different speeds on road corresponding to the amplitude value less than 7 mm
根据表6可知,对于惯性质量为526 kg的机电悬架,当输入信号幅值小于7 mm时,不会使机电减振器起作用,相当于此时无电磁阻尼,根据簧载质量加速度幅频特性,高频时阻尼越小,越有利于降低簧载质量的加速度,因此滤振有利于高频平顺性的提升。
3.2 增加滤振缓冲器的模型
由于电机转子等效的转动惯量换算后的惯性质量达到悬架惯性质量的91.7%,为简化模型,假定所有惯性质量均集中在电机转子上,滤振缓冲器配置于负重轮与电机转子之间,因此2自由度模型如图14所示。图14中,zh为滤振缓冲器的输出位移,kh为缓冲器等效弹簧刚度,ch为缓冲器等效阻尼系数。
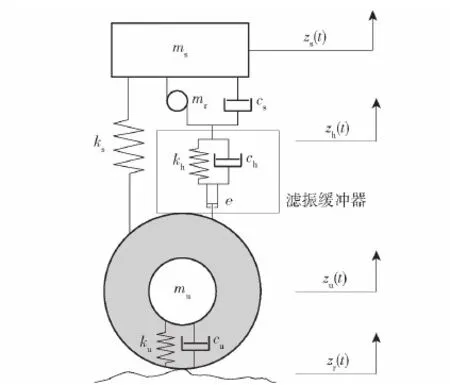
图14 增加滤振缓冲器的2自由度悬架模型图Fig.14 Diagram of 2DOF suspension model with vibration filtering buffer
因此,负重轮相对簧载质量的相对位移通过滤振缓冲器的过滤和缓冲后,驱动惯性质量运动,从而能够有效地降低惯性质量引起的惯性力。
根据图14所示模型建立数学模型,如式(24)、式(25)所示。
当|zu-zs|≤e时
(24)
当|zu-zs|>e时
(25)
应用式(1)~式(8)、式(12)、式(13)、式(24)、式(25),在MATLAB软件中应用Simulink建立有无滤振缓冲器2自由度机电悬架的仿真对比模型。该模型以时域D级路面作为2自由度悬架激励,从而对比分析悬架特性指标的变化,并计算均方根值。
3.3 滤振缓冲器的结构原理
滤振缓冲器如图15所示。该滤振缓冲器安装于传动装置与电机转子之间,主要由从动轴、缓冲块、主动轴、从动轴盖(图中隐去)、螺钉、平键构成。从动轴通过平键与电机转子连接;主动轴通过花键与变速器输出轴连接。主动轴与左右缓冲块之间的间隙为角度A和B。当传递的振动为顺时针方向旋转时,当振动角度小于或等于间隙角度A时,主动轴振动不足以克服间隙角度A,则随机振动不能通过主动轴传递到缓冲块,从而实现滤振。当振动角度大于间隙角度A时,主动轴克服间隙角度A,通过主动轴的撞击块与缓冲块发生面接触,振动通过缓冲块的变形缓冲后传递给电机轴。当上述振动的运动方向反向时,若振动的角度小于或等于间隙角度A+B,则主动轴不足以克服间隙角度A+B,从而实现滤振,若振动的角度大于间隙角度A+B,则主动轴的撞击块与缓冲块发生面接触,振动通过缓冲块的变形缓冲,通过平键将滤振与缓冲后的振动传递给电机轴。
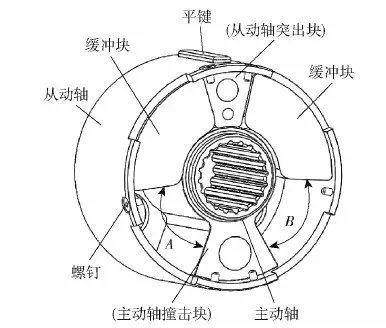
图15 滤振缓冲器结构Fig.15 Vibration filtering buffer structure
3.4 滤振与缓冲对阻尼特性的影响分析
根据文献[23]可得未加滤振缓冲器时机电执行器阻尼力矩Ts的计算公式为
(26)
式中:θr为电机的旋转角度;其余电机参数如表7所示。

表7 电机与缓冲器参数表Table 7 Motor and buffer parameters
根据式(10),计算出电机轴向滤振角度θe=βseirixid=1.065 rad。
当增加滤振缓冲器后,机电执行器阻尼力矩Tsh的计算公式为
(27)
式中:Th为缓冲器的力矩值,
(28)
将执行器的摇臂置于水平位置,在垂向分别以频率1 Hz幅值100 mm、频率10 Hz幅值2 mm的正弦信号输入摇臂末端,得到机电执行器的力- 位移曲线如图16所示,力- 速度曲线如图17所示。
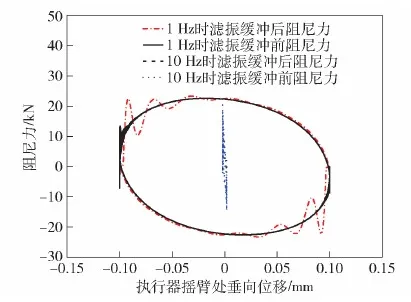
图16 执行器力- 位移特性Fig.16 Actuator force-displacement characteristics
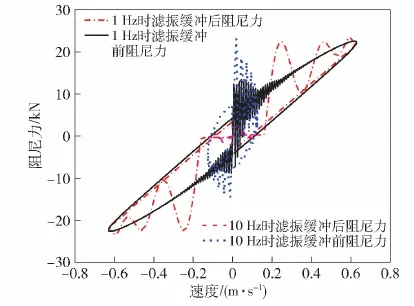
图17 执行器力- 速度特性Fig.17 Actuator force-speed characteristics
通过仿真可得到如下结论:滤振会增大低频激励时执行器的输出力变化,这是由于间隙造成撞击引起的;滤振能够滤除高频小幅振动,大幅削减惯性力;缓冲能够将执行器在换向时的惯性力引起的高频振动冲击转换成低频振动,使瞬态冲击得到缓冲,缓冲器的刚度越小,则曲线越平缓。
3.5 滤振与缓冲参数的匹配
通过悬架滤振幅值的计算可得缓冲器间隙的数值,设计缓冲器时参考该数值。缓冲器的阻尼值与其温升、寿命相关,应尽可能小。缓冲器的刚度设计要充分考虑机电执行器主动控制的最小时滞要求、缓冲器的使用寿命、空间尺寸约束,同时要综合比较应用缓冲器后执行器各频段的缓冲效果,实现示功图饱满、波动幅值小。
为此本文提出评价缓冲器刚度优化的方法:计算不同刚度值时1~10 Hz整数频率正弦信号(幅值分别对应100 mm、80 mm、60 mm、50 mm、40 mm、20 mm、10 mm、6 mm、4 mm、2 mm)激励下的阻尼力,采样率为1 kHz,计算各频率下阻尼力的标准差Fsj,j=1,2,…,10,其计算公式如式(29)所示,最终得各频率阻尼力标准差的均值Fs,其计算公式如式(30)所示,结果如图18所示,则数值最小时对应的刚度为最优刚度值。
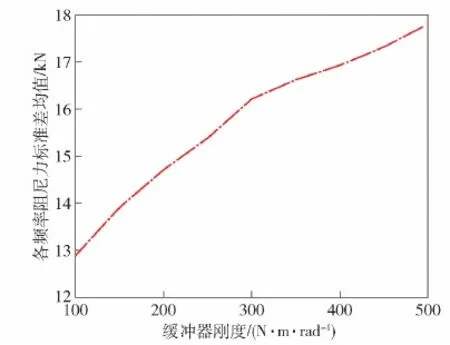
图18 各频率阻尼力标准差均值与缓冲器刚度关系Fig.18 Relationship between mean value of standard deviation of damping force at each frequency and buffer stiffness
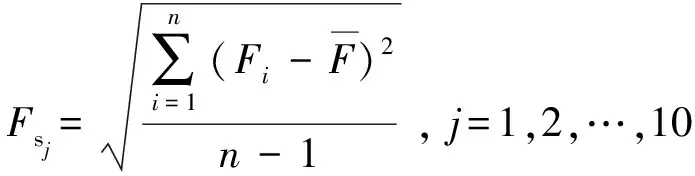
(29)
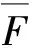
(30)
从图18中可知,缓冲器的刚度增大造成阻尼力标准差均值增大,会加大阻尼力的波动。因此刚度值需要综合主动控制时滞、缓冲弹性体寿命、阻尼力波动等因素,本文缓冲器的刚度为259 N·m/rad,缓冲器的阻尼系数为0.1 N·ms/rad。
悬架的缓冲器等效刚度与阻尼计算如下:
kh=βsirixidkhs/Ry
(31)
ch=βsirixidchs/Ry
(32)
4 滤振缓冲仿真对比分析
为验证滤振缓冲措施的效果,以不同等级的路面输入作为2自由度悬架模型的激励,计算时域下惯性质量的惯性力、簧载质量加速度、相对动载荷、悬架动挠度的均方根值。表8为D级路面40 km/h时3种状态的悬架特性对比。
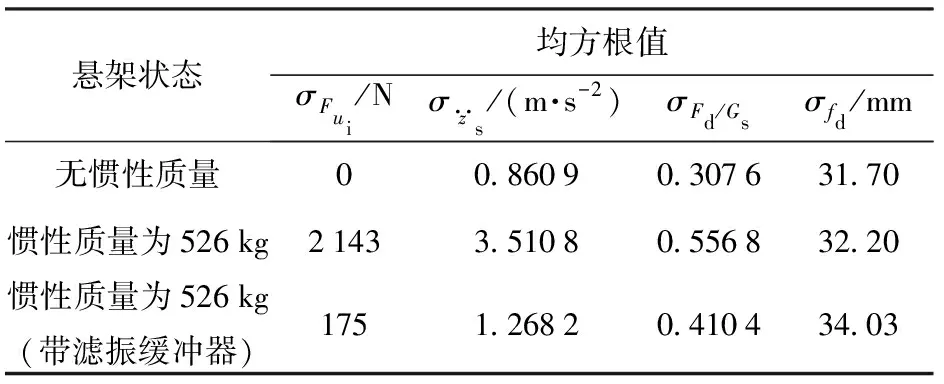
表8 D级路面40 km/h时3种状态的悬架特性对比Table 8 Comparison of suspension characteristics for the three states at 40 km/h on Class D road
由表8可见:当采用滤振缓冲器后,惯性质量为526 kg时,其惯性力的均方根值为175 N,相对原惯性力的均方根值2 143 N,有大幅降低,基本消除了惯性质量的不利影响;加速度均方根值相对原3.510 8 m/s2降低至1.268 2 m/s2,负重轮相对动载荷由0.554 8降低至0.410 4,悬架动挠度由32.20 mm增大至34.03 mm。因此滤振缓冲器发挥了较好的作用,降低了惯性质量的不利影响。有滤振缓冲的惯性力的功率谱密度如图19所示,相对无滤振缓冲措施而言,其功率谱密度得到了大幅降低。
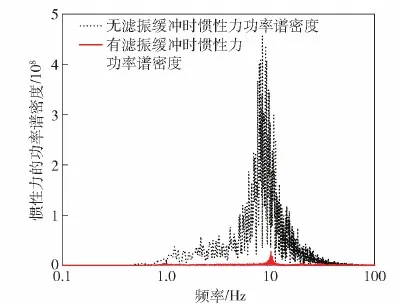
图19 有无滤振缓冲惯性力的功率谱密度对比Fig.19 Comparison of power spectral density of inertial force with or without vibration filtering and buffering measures
5 台架试验验证
5.1 惯性力的台架对比测试
为评价滤振缓冲的效果,需要采集内齿圏应力。测试选用日本TML公司DRA-30A多通道动静态应变仪,配合PC进行在线测量,应力台架测试如图20所示。

图20 机电悬架的台架试验Fig.20 Bench test of electromechanical suspension
为获得内齿圈在试验台路面模拟时的动态啮合力的大小及内齿圈的分布情况,布置的应变片测点如图21所示。测点分布内齿圈上,沿内齿圈均布 4组应变片,每组6片;在相邻3齿的齿根处及每个齿的齿宽方向布置2片,从而获得周向与内齿向的齿根应变和应力大小。
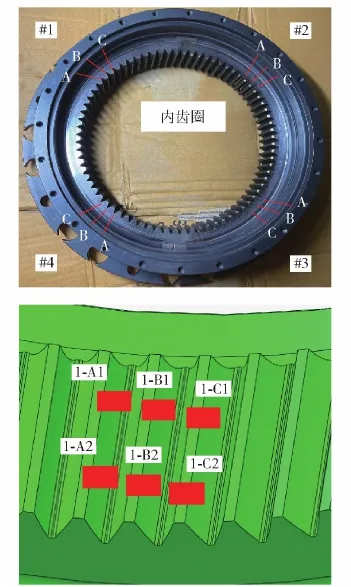
图21 内齿圈的测点分布Fig.21 Measuring point distribution of inner gear ring
液压振动台激振器输出D级路面行驶速度 40 km/h 的振动位移,得到其中一组的内齿圈径向应力对比如图22所示,无滤振时内齿圈齿根切向应力峰值较多,最大达到519.9 MPa,有滤振缓冲时峰值得到衰减,切向应力最大值为110.1 MPa。

图22 有无滤振缓冲措施的内齿圈应力对比Fig.22 Stress comparison of inner gear ring with or without vibration filtering and buffering measures
5.2 悬架性能的台架对比测试
5.2.1 特定频点的对比测试
为验证对惯性力集中区域(4.32~17.78 Hz)的滤振缓冲效果,进行台架试验,悬架配置为馈能耗散模式,负载电阻为100 Ω,如图20所示。选取特定频点进行测试,得到测结果如表9所示。
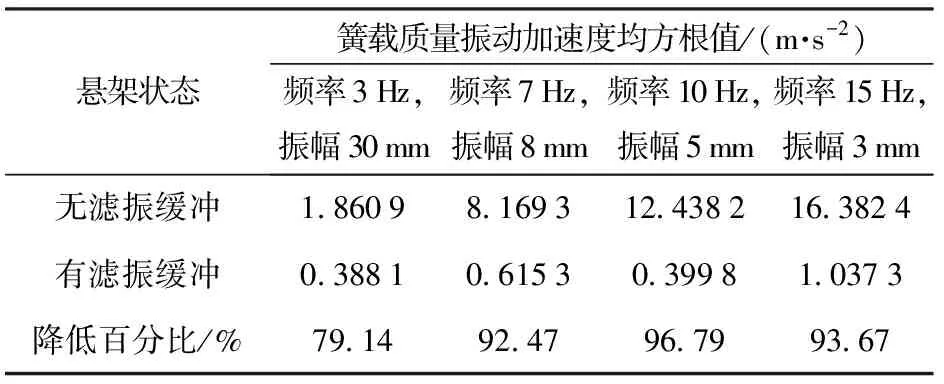
表9 多频点台架试验悬架特性对比Table 9 Comparison of suspension characteristics in multi-frequency bench test
从表9中可知:在测试的各个频点,簧载质量的加速度值均得到大幅降低,最高降幅达到96.79%;增加滤振缓冲措施的机电悬架相对原机电悬架能够较好地消减惯性质量的恶劣影响,使悬架的平顺性得到较大提升。
5.2.2 随机路面激励的对比测试
为验证滤振缓冲的效果,在试验台上输出D级路面行驶速度40 km/h的振动位移,测试机电悬架,得到簧载质量加速度的对比情况如图23所示,悬架特性对比如表10所示。
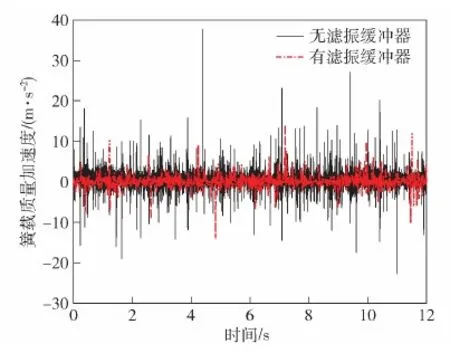
图23 有无滤振缓冲器的簧载质量加速度对比Fig.23 Comparison of sprung mass acceleration with and without vibration filtering buffer
由表10可知,通过台架试验,验证滤振缓冲措施有效,当采用滤振缓冲器后,加速度均方根值相对无滤振缓冲时的5.821 5 m/s2降低至2.524 3 m/s2,负重轮相对动载荷由0.832 4降低至0.712 1;悬架动挠度由35.43 mm增大至38.32 mm。
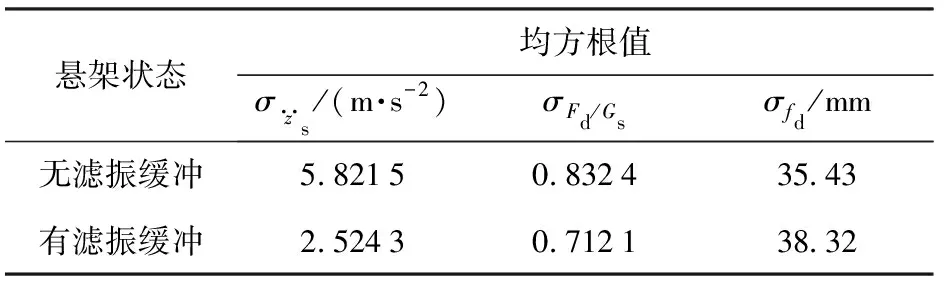
表10 D级路面台架试验悬架特性对比Table 10 Comparison of suspension characteristics in bench test of Class D road
综上所述,台架试验结果表明,滤振缓冲器发挥了较好的作用,降低了惯性质量的不利影响。
6 结论
1)随着车速的增大,簧载质量加速度的均方根值相对无惯性质量的悬架显著增大,同时惯性质量越大,则簧载质量加速度的均方根值越大。
2)本文机电悬架的惯性质量为526 kg时,惯性力的功率谱密度在第二主频附近(3.98~17.78 Hz),功率谱密度值较大,说明惯性质量造成第二主频区振动剧烈。
3)台架试验D级路面40 km/h的行驶速度时,机电悬架固定齿圈应力对比:无滤振时齿圈齿根切向应力峰值较多,最大达到519.9 MPa,滤振缓冲后峰值得到衰减,切向应力最大值为110.1 MPa。
4)采用滤振缓冲措施,相对无滤振缓冲的机电悬架而言,惯性力的功率谱密度得到大幅降低。
5)本文所提滤振缓冲器经仿真台架试验验证,可以滤除大量机电悬架的惯性力,提升了悬架平顺性。
