活性药型罩聚能装药侵彻爆燃试验及耦合作用机理分析

2023-03-21苏成海李宗谕郑元枫郑志坚郭焕果

兵工学报 2023年2期

苏成海，李宗谕，郑元枫，郑志坚，郭焕果

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081； 2.保利澳瑞凯(山东)矿业服务有限公司，山东威海 264200)

0 引言

现代战争中，能否对装甲目标进行有效打击，对战争成败与进程有决定性影响。特别是随着战场装甲目标多样化，使聚能战斗部打击目标类型和应用范围得到拓展的同时，也对其毁伤机理、毁伤模式和毁伤能力提出了新的挑战性要求。从高效毁伤角度看，在打击轻中型装甲目标时，对聚能战斗部毁伤效能和毁伤模式的要求更侧重于具有强内爆或大开孔毁伤能力，与传统金属射流侧重大破甲深度截然不同[1-3]。

活性药型罩聚能装药技术是一种新概念高效毁伤技术，这种聚能装药使用的活性药型罩不同于传统惰性金属罩，这类活性药型罩在装药爆轰下形成的活性射流，既能利用动能对目标实行侵彻/破甲毁伤，更能利用自身化学能释放提升射流开孔孔径或提高后效毁伤效应[4-5]。目前，从配方体系来看，主要包括氟聚物基、金属间化合物、合金类、非晶类等活性药型罩。

活性药型罩聚能装药对目标特有的侵爆耦合毁伤模式，使其在近年来受到广泛研究和关注。国外方面，2001年，Baker等[6]提出了一种整体聚爆活性药型罩聚能战斗部，并通过X光试验验证了活性药型罩在聚能装药爆轰压力作用下可有效形成与铝射流类似的连续射流，进一步毁伤实验表明，在0.5～1.5倍装药直径小炸高条件下，活性药型罩(包括氧平衡型、富氧型和缺氧型3种)聚能装药可显著提高对混凝土靶的毁伤效应，当炸高超过2倍装药直径后毁伤效应下降。2007年，Daniels等[7]对活性药型罩聚能战斗部作用混凝土和跑道目标进行了毁伤试验研究，试验结果表明，在1倍装药直径炸高下，口径216 mm活性药型罩聚能战斗部可一举摧毁尺寸φ1.5 m×2 m柱形钢箍混凝土墩靶，对标准三层结构沥青混凝土公路靶标造成的炸坑直径约1.5 m，对尺寸1.5 m×1.5 m×5.5 m钢筋混凝土桥墩的毁伤增强效应也相当显著。

国内方面，肖建光等研究了聚四氟乙烯(PTFE)/Al活性药型罩聚能装药对混凝土靶的侵爆毁伤效应，建立了混凝土靶毁伤模型，结果表明，活性药型罩壁厚和锥角对活性射流侵爆毁伤效应有显著影响[8-9]。Zheng等[10-11]采用静爆实验研究了PTFE/Al与PTFE/W/Cu/Hf活性药型罩聚能装药对多层间隔靶的毁伤效应，结果表明，后效铝靶的爆裂毁伤效应主要取决于随进活性材料的质量。张先锋等开展了以Al/Ni为代表的含能结构材料冲击压缩细观模拟研究，研究了材料配比、制备工艺对材料细观结构的影响规律[12]，并设计了一种基于K装药结构的Al/Ni-Cu双层含能药型罩聚能装药结构。结果表明，相对于Cu-Cu药型罩，新设计的装药结构对钢靶的侵彻深度和侵彻体积分别提高了20.1%和23.0%，对混凝土靶的侵彻深度和侵彻体积分别提高了17.2%和45.6%[13]。李延等采用光滑粒子流体动力学(SPH)数值模拟和脉冲X光实验研究了PTFE/Ti/W活性射流成型特性，分析了活性射流成型过程中的膨胀现象[14]，并开展了PTFE基含能药型罩动态释能特性研究，研究结果表明，相比于Al射流，含能射流超压峰值可提升3～4倍[15]。高本兵等[16]采用SPH数值模拟方法和实验对比分析了PTFE与PTFE/Cu活性射流成型特性与侵彻性能。辛春亮等[17]研究了PTFE/Al活性射流对钢靶的侵彻特性及靶后纵火能力。

由此可见，国内外在活性药型罩聚能装药研究领域已取得一定进展，但上述研究更侧重于活性药型罩聚能装药对目标毁伤效应的验证，在机理性、规律性和理论模型方面的研究有待加强。

本文以氟聚物基活性药型罩聚能装药为研究对象，重点围绕炸高对钢靶毁伤影响行为进行研究，揭示其影响规律与机理并建立理论模型。

1 活性药型罩聚能装药作用钢靶实验

1.1 活性药型罩制备及材料特性

实验用活性药型罩材料由PTFE和铝粉按照73.5%/26.5%的质量配比组成，其中氟聚物PTFE分子式为-[C2F4]n-。活性药型罩具体制备过程如下：

1)将PTFE粉体放置在82 ℃恒温真空环境内干燥5 h，经高温脱水处理后，PTFE粉体不易粘接成块。随后向干燥后的PTFE粉体中缓慢多次添加铝粉进行预混合，再将预混合粉体放入V型桶混料机进行干法混合，混合时间2 h，由此得到均匀混合的活性材料粉体。

2)称量一定质量的活性材料粉体，通过粗筛网将其加入准备好的模具中，均匀分散。再采用压机在300 MPa预制压力下保压1 min，随后取出试样。

3)在氮气保护下，对冷压成型的活性药型罩进行烧结硬化处理，具体烧结温度曲线如图1所示。烧结时首先以50 ℃/h的速度将温度升到380 ℃，然后在该温度下保持4 h，随后以50 ℃/h的速度进行降温，降温至310 ℃时，保温2 h，最后冷却至室温。

图1 活性药型罩样品烧结曲线Fig.1 Sintering curve of reactive liner samples

图2 活性药型罩Fig.2 Reactive liner sample

图2所示为活性药型罩理论结构和实物样品，经排水法测试，制备得到的活性药型罩样品平均密度为2.27 g/cm3。活性药型罩材料差示扫描量热法(DSC)与热重分析法(TG)热分析结果表明[18]，PTFE/Al活性材料热稳定性较好，当温度超过510 ℃时，PTFE基体迅速分解，释放强氧化剂，并与铝颗粒发生剧烈的化学反应，释放大量化学能和气体产物。图3所示为活性药型罩扫描电子显微镜(SEM)微观结构，从中可以发现烧结后的活性药型罩样品中，铝颗粒呈近圆形，且较为均匀地分布在PTFE基体内。此外，通过准静态与动态力学性能测试，对活性药型罩材料机械性能参数进行标定，其与紫铜相关参数对比列于表1。

图3 PTFE/Al活性药型罩SEM微观结构Fig.3 SEM microstructure of PTFE/Al reactive liner

表1 PTFE/Al活性材料与紫铜机械性能参数对比Table 1 Comparison between mechanical parameters of the reactive material and copper

1.2 实验原理与结果

实验所用活性药型罩聚能装药主要包括锥形活性罩、装药和壳体，如图4所示。实验采用船尾形装药，由8701炸药压制而成，装药密度约1.70 g/cm3，壳体材料为LY12硬铝，厚度为2 mm。装配过程中，通过虫漆粘合活性罩与8701药柱，活性罩贴合摆差控制在0.3 mm以内，随后在8701药柱外表面涂抹沥青漆入壳，通过压紧螺栓紧固。

图4 活性药型罩聚能装药结构Fig.4 Reactive liner shaped charge structure

图5为活性药型罩聚能装药作用钢靶实验原理与靶场布置，活性药型罩聚能装药、炸高筒、钢靶从上至下放置在钢底座上，通过改变炸高筒高度控制实验变量，实验中炸高分别为0.35CD、0.50CD、1.00CD、1.50CD与2.0CD(CD为装药直径)。钢靶尺寸φ120 mm×100 mm，材料为45号钢。

图5 实验原理与靶场布置Fig.5 Experimental principle and setup

活性罩聚能装药在不同炸高下的钢靶毁伤实验结果如图6所示，钢靶毁伤剖视图如图7所示，相关数据列于表2。结合图6和表2可以发现：当炸高从0.35CD增大至1.5CD时，活性罩聚能装药产生的活性射流对钢靶的侵彻深度变化较小；当炸高增加到2.0CD时，活性射流对钢靶的侵彻深度大幅下降；进一步地，随着炸高增大，在钢靶上产生的侵孔直径整体呈减小趋势；更重要的是，当炸高不大于1.0CD时，活性射流还在钢靶上造成了多条径向裂纹。

具体而言，活性罩聚能装药炸高为0.35CD时，在钢靶上产生4条平均宽度分别为6.2 mm、5.1 mm、7.6 mm和0.8 mm的径向裂纹，且3条粗裂纹均贯穿至钢靶外侧面。剖视图进一步表明侵孔孔径沿侵彻深度方向近似线性减小。炸高为0.5CD时，活性射流作用钢靶产生3条径向裂纹，导致钢靶几乎碎裂为两部分，3条径向裂纹平均宽度分别为16.5 mm、14.8 mm和1.6 mm；侵孔孔径沿侵彻深度方向也呈近似线性减小。炸高为1.0CD时，活性射流作用钢靶产生4条径向裂纹，其中2条裂纹贯穿钢靶，1条裂纹近乎贯穿，1条裂纹较为细微，裂纹平均宽度分别为1.5 mm、1.3 mm、1.0 mm和0.3 mm；侵孔剖面轮廓线呈较为不规则的折线状，上端孔径大，下端孔径明显变小。炸高为1.5CD时，钢靶未发生碎裂，无裂纹产生，侵孔细长，孔径沿侵彻深度方向近线性减小。炸高为2.0CD时，活性射流对钢靶侵彻深度明显下降，仅在钢靶上产生1个半圆形浅坑。

图6 活性罩聚能装药作用钢靶实验结果Fig.6 Experimental results of damage effectscaused by the reactive liner shaped charge to the steel target

图7 钢靶破坏剖视图Fig.7 Section view of damage effects

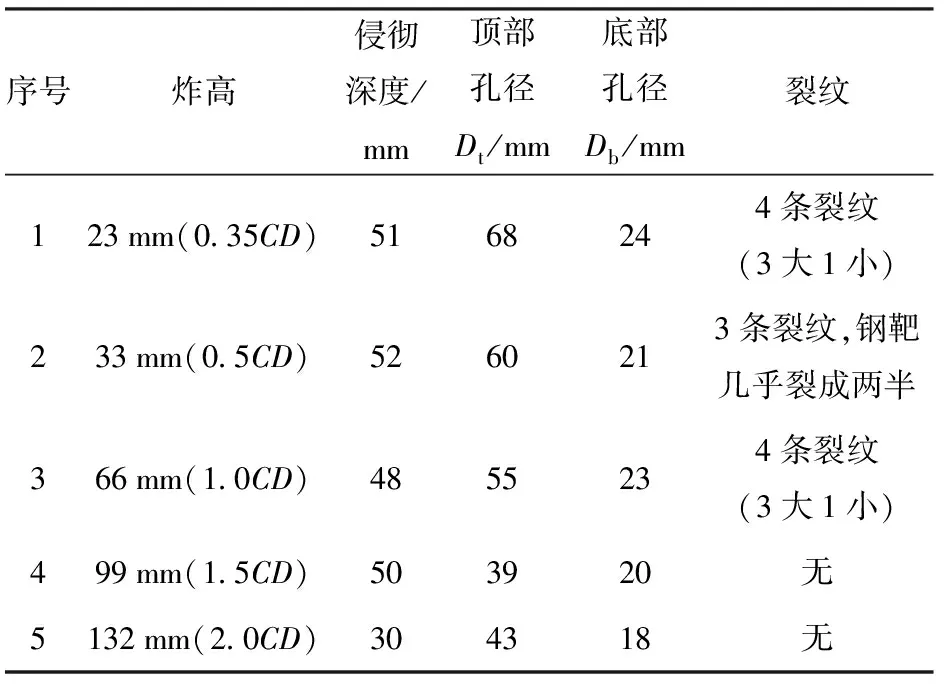
表2 活性罩聚能装药作用钢靶实验数据Table 2 Experimental results regarding damage effects

1.3 机理讨论

从机理上分析，活性药型罩聚能装药产生的活性射流对钢靶的毁伤过程主要包括射流成型、射流拉伸、射流侵彻和射流内爆4个主要阶段，如图8所示。

图8 活性罩聚能装药对钢靶毁伤作用原理Fig.8 Schematic diagram of the damage effects

射流成型和拉伸阶段，活性药型罩在聚能装药爆轰作用下被压垮并在轴线碰撞，罩内层形成射流、罩外层形成杵体，在宏观上，所形成的活性射流存在很大的速度梯度，造成射流拉伸。更为重要的是，在射流成型过程中，装药爆轰导致冲击波扫过活性药型罩，且药型罩在轴线闭合过程中内部还会发生剧烈碰撞，同时活性材料内部各组分严重变形且相互摩擦，这些均会导致药型罩内部温度急剧上升。进一步，在冲击引发热效应作用下，活性射流内部基体开始发生分解反应，释放具有强氧化性的气体产物C2F4，主要反应过程为

-[C2F4]n-→nC2F4(g)

(1)

式中：n为高聚物的聚合度。

基体分解释放的气体产物将与铝粉发生放热反应，主要反应过程为

4Al+3C2F4→4AlF3(g)+6C

(2)

4Al+C2F4→4AlF+2C

(3)

2Al+C2F4→2AlF2(g)+2C

(4)

需要强调的是，在成型与拉伸阶段，活性射流会在一定程度上发生如式(1)所描述的基体分解，分解产物也可能与铝粉在一定程度上发生如式(2)～式(4)所描述的放热反应。但是，大量研究表明[9-11，14]，在射流成型与拉伸阶段，这些反应并不显著。事实上，活性射流的激活和爆燃反应是一个典型的力- 热- 化学耦合作用过程，成型和拉伸过程中基体的分解需要一定时间，且基体分解产物和铝粉间需要经过一定的反应增长过程才会发生剧烈的爆燃反应。即活性射流爆燃反应具有延迟性，这种延迟特性使得活性射流能够在宏观上成型并利用自身动能实现对目标的侵彻。一般地，将活性药型罩受到冲击开始到活性射流发生剧烈爆燃反应的时间间隔称为反应延迟时间，且常忽略延迟时间之前活性射流的化学反应，即假设活性射流在其反应延迟时间前是惰性的，当到达反应延迟时间时，活性射流瞬间发生剧烈的爆燃反应。

图8(c)所示为活性射流侵彻阶段，待射流侵彻至反应延迟时间时，侵孔内射流瞬间发生剧烈的爆燃反应，造成侵孔内压力骤升，进一步实现对钢靶的扩孔，如图8(d)所示。与此同时，活性射流在侵孔内的内爆效应造成侵孔周围的钢靶内部微元处于径向受压，环向受拉状态，从而可能导致径向裂纹的产生。

基于上述讨论，再结合1.2节的实验结果，可进一步分析炸高对毁伤效应的影响机理。炸高在0.35CD到1.0CD范围内，活性射流撞击钢靶瞬间头部较粗，开孔孔径较大，有利于更多的活性材料进入侵孔内部，随之在侵孔内部爆燃反应产生的超压较高，最终造成钢靶内侵孔孔径增大，伴随多条贯穿式裂纹，结构破坏明显。随着炸高增加到1.5CD，活性射流充分拉伸后直径较小，导致侵孔孔径小，进入侵孔内的活性材料质量少，内爆效应减弱，钢靶上不再有径向裂纹。若炸高继续增加到2.0CD，则活性射流侵彻深度也大幅下降，这是因为活性药型罩材料抗拉强度和断裂拉伸率明显低于传统紫铜材料(见表1)，因此在大炸高下活性射流更易发生颈缩和断裂，导致侵彻能力显著下降。

2 活性射流作用钢靶侵爆理论模型

2.1 活性射流侵彻与延迟时间

根据准定常不可压缩流体力学理论[19]建立活性射流侵彻模型，基于虚拟原点理论可以得到图9所示侵彻深度与侵彻时间关系图。图9中，纵轴y为轴向距离且以活性药型罩底部为0点，横轴t为时间，t0为活性射流头部到达靶板时间，O(ta，a)为虚拟原点坐标，ta为爆轰波到达虚拟原点的时间，a为虚拟原点相对距离，τ为活性射流反应延迟时间，H为活性药型罩聚能装药炸高，BM段为活性射流侵彻阶段，MP段为传统射流后续侵彻阶段，L为活性射流最大侵彻深度，Lmax为传统射流最大侵彻深度。

图9 活性射流侵彻钢靶理论模型Fig.9 Theoretical model for the reactive jet penetrating the steel target

由图9可知，对BM段上任一点，对应侵彻时间为t，侵彻深度为L′，则

(t-ta)vj=L′+H-a

(5)

式中：vj为活性射流头部速度。

对t微分，由于H-a是常数，且活性射流对钢靶的侵彻速度u=dL′/dt，则有

(6)

对式(6)在BM段上积分，可得

(7)

式中：vj0为活性射流碰靶时刻头部速度。

对式(7)进行变换，可得

(8)

对于点M，其侵彻时间t=τ，侵彻深度L′=L，则式(5)可写为

(9)

对理想不可压缩流体，有

(10)

式中：ρt与ρj分别为钢靶板与活性射流密度。

由式(10)可得

(11)

将式(11)代入式(9)，可得

(12)

式(12)也可转化为侵彻深度L和延迟时间τ的关系：

(13)

2.2 活性射流有效质量

为研究活性射流对钢靶的爆裂毁伤行为，需要计算活性射流在侵彻过程中随入侵孔内的活性材料有效质量。假设活性射流在侵彻过程中完全不反应，到达反应延迟时间τ发生瞬间反应；活性射流为均匀圆柱形，当活性射流到达钢靶时，射流初始长度刚好等于炸高。利用微分原理，将射流离散为各个微元，在侵彻过程中，每一段微元的速度与质量保持不变，忽略微元内速度梯度。

活性射流各微元间具有速度梯度，在侵彻钢靶过程中射流仍会拉长，根据准静态流体力学理论，活性射流速度沿轴线呈近线性分布，其侵彻过程可以描述为以虚拟原点O(ta，a)为起点的射线簇，如图10所示。图10中，r为射流半径，l为活性射流长度；将活性射流离散为1～k个微元 (k≥2)，下标i代表第i个射流微元，vi为第i个活性射流微元的速度，vk为第k个活性射流微元的速度，即活性射流尾部微元的速度；dv为任意活性射流微元的体积。

图10 活性射流侵彻钢靶剩余质量模型Fig.10 Residual mass model of the reactive jet penetrating the steel target

各条射线斜率代表了对应微元的速度，活性射流分为射流与杵体两部分，假设射流部分质量为m，当侵彻至深度L时，活性射流前1-i段对钢靶进行侵彻和扩孔，同时在侵孔内形成活性材料堆积，该段即为活性射流侵爆钢靶的有效质量meff，而此后i+1至k段射流即为剩余质量mres，在到达活性射流反应延迟时间τ时，剩余质量mres对钢靶产生的作用可忽略不计，二者关系如式(14)所示。由图10可知，每段射流微元的体积可表示为式(15)：

meff=m-mres

(14)

dV=πr2dl

(15)

有效质量与射流总质量为

meff=ρjπr2lim=ρjπr2lk

(16)

(17)

式中：li为第i个活性射流微元至射流头部的距离；lk为第k个活性射流微元至射流头部的距离。

考虑射流是连续的，且速度沿射流母线方向呈线性分布，当射流微元趋近于无穷大时，射流长度比可用速度比替代：

(18)

(19)

式中：vi为第i段射流微元的速度；vt为活性射流尾部速度。活性射流速度之间的关系由式(12)可得

(20)

基于活性射流速度分布研究[10]，射流头部速度与尾部速度之间关系可近似为vt≈0.2vj，因此

(21)

2.3 钢靶扩孔与爆裂

射流在侵彻过程中，射流头部与钢靶内的压力p满足Held[20]与Alekseevskii[21]所修正的伯努利方程：

(22)

式中：Rt为靶板强度。

活性射流侵彻靶板时，假设射流头部为半圆形，冲击波在其头部形成驻点，射流材料在头部堆积。在驻点处，活性射流速度由vj降低至u，根据动量守恒原理，活性射流作用在堆积区的合力Fc为

(23)

式中：rj为活性射流头部微元半径。则沿轴向的受力F可表示为

(24)

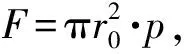
(25)

在此基础上，活性射流对钢锭扩孔过程实质为作用在孔壁的压力克服靶板强度使孔径增大的过程，Szendrei[22]认为孔径的初始增长速度等于射流轴向侵彻速度，且靶板孔壁处的压力与开孔面积的乘积保持为常数。根据伯努利方程，第i段微元孔壁压力pi为

(26)

式中：ur,i为第i段射流微元与孔壁作用时孔径的扩孔速度。假设射流微元轴向侵彻时间与径向扩孔作用时间相同，则径向扩孔速度表达式为

(27)

式中：rc,i为第i段微元侵彻时的扩孔半径。

随着rc的增加，u逐渐降低，当u=0 m/s时对式(27)积分，可得活性射流动能侵彻靶板最大孔径rp为

(28)

式中：p0为活性射流初始扩孔压力。到达反应延迟时间τ时，活性射流瞬间发生爆燃反应，在侵孔内产生内爆压力p，由此可得活性射流侵爆耦合作用钢靶最大扩孔半径rmax为

(29)

内爆压力取决于活性射流有效质量，其计算公式[23]为

(30)

式中：cv为定容比热；T为温度；V为比容。

Alekseevskii[21]采用流体动力学方法近似描述弹体的流体侵彻过程，根据弹、靶界面应力平衡关系基本方程建立了A-T模型，靶板的阻抗可表述为

(31)

式中：σyt为靶板屈服强度；Et为靶板弹性模量。

进一步地，钢靶爆裂现象的本质是在活性材料发生化学反应后，钢靶内部应力超过钢靶应力极限，导致钢靶出现结构破坏，其结构破坏基本模型可简化为圆筒的结构失效行为[24]。工程中将圆筒根据径比分为薄壁与厚壁两种，径比K的计算如式(32)所示。一般将K>1.2称为厚壁，则活性射流对钢靶的爆裂作用可归类为厚壁圆筒在内压作用下的失效行为：

(32)

式中：D为钢靶直径；Da为侵孔平均直径。

厚壁圆筒在内压作用下，各个微元同时处于径向应力、环向应力与轴向应力作用下[25]，厚壁圆筒在工程中的失效准则判定，分为第一、二、三、四强度理论和中径判定理论，其中又以第四强度判定理论与实际最贴合，因此选择第四强度理论作为钢靶失效判定准则，其与径比K的关系如式(33)所示：

(33)

式中：σb为实验用45号钢的抗剪强度，取178 MPa。

3 活性射流作用钢靶侵爆毁伤计算

3.1 侵彻深度计算与延迟时间分析

图11 不同炸高条件侵彻深度随时间变化关系Fig.11 Relationship between penetration depth and time under different stand-offs

基于2.1节活性射流侵彻模型，可以获得活性射流反应延迟时间近似值。依据式(13)，分别得出活性射流在不同炸高下侵彻深度随时间变化关系，如图11所示，再结合表2给出的侵彻深度实验值，可以反推出活性射流反应延迟时间。图11中A点为炸高2.0CD条件下所对应的反应延迟时间为49.3 μs；B点为炸高1.5CD条件下所对应的反应延迟时间为68.2 μs；C点为炸高1.0CD条件下所对应的反应延迟时间为66.1 μs；D点为炸高0.5CD条件下所对应的反应延迟时间为86.4 μs；E点为炸高0.35CD条件下所对应的反应延迟时间为86.1 μs。此外，当炸高为2.0CD时，由于活性射流侵彻能力严重下降，仅能在钢靶上产生半圆形的浅坑，其侵彻行为已经与其他炸高条件下明显不同，因此后续计算不再考虑2.0CD条件下的情况。对除A点以外其他4点获得的反应延迟时间进行平均，即可得到该装药条件下活性射流反应延迟时间近似值τ=78.4 μs。

3.2 活性射流有效质量计算

基于2.2节中给出的活性射流随进侵孔有效质量模型，对活性射流在反应延迟时间内进入侵孔内的有效质量进行计算。首先，获得不同炸高条件下活性射流有效质量随侵彻深度变化关系，如图12所示，再结合表2给出的侵彻深度实验值，可以得到各个炸高下对应的侵孔内活性射流有效质量，其中A点为炸高1.5CD条件下对应活性材料有效随进质量16.2 g；B点为炸高1.0CD条件下对应活性材料有效随进质量18.7 g；C点为炸高0.5CD条件下对应活性材料有效随进质量23.7 g；D点为炸高0.35CD条件下对应活性材料有效随进质量25.1 g。

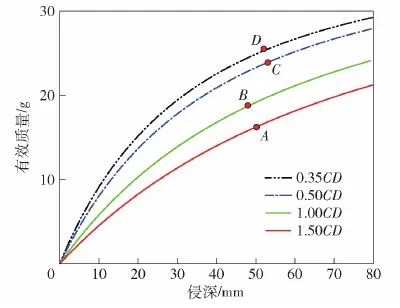
图12 不同炸高条件活性射流有效质量随侵彻深度变化关系Fig.12 Relationship between meff and penetration depth under different stand-offs

3.3 侵孔直径计算与爆裂分析

活性射流对钢靶的破坏作用，是通过侵彻和内爆效应时序耦合进行的，在3.1节与3.2节中，通过理论计算与实验结果相结合，对实验所用活性材料反应延迟时间以及有效随进质量进行了计算。到达反应延迟时间后，活性射流有效质量在侵孔内发生剧烈的爆燃反应，产生的超压对钢靶造成二次结构破坏，当超压大于一定阈值时钢靶发生碎裂。

为获取侵孔直径理论计算时的初始参数，基于AUTODYN-2D有限元仿真平台，采用二维Euler算法，对活性射流着靶时各项物理参数进行计算，活性材料使用SHOCK状态方程和Johnson-Cook强度模型加以描述，材料参数取自文献[10]，射流成型计算网格大小为0.2 mm×0.2 mm，着靶参数计算结果列于表3。根据式(29)，可以获得活性射流侵爆钢靶产生的顶部孔径Dt和底部孔径为Db，计算结果列于表4，其与实验值对比如图13所示。

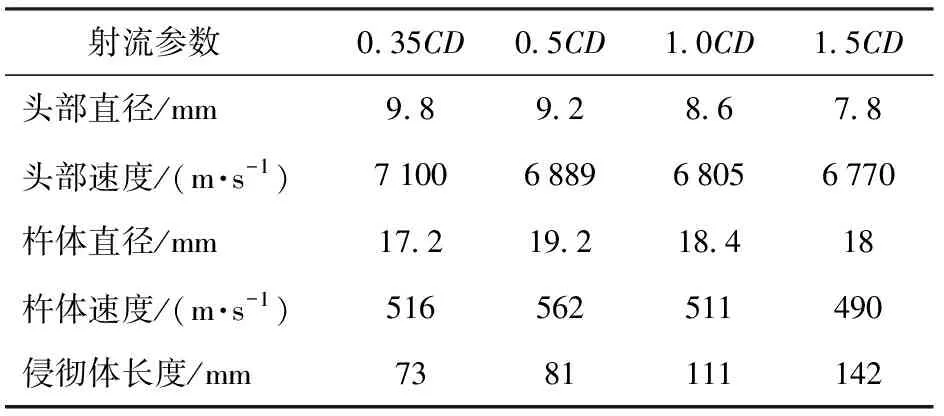
表3 着靶时活性射流物理参数Table 3 Parameters of the reactive jet when reaching the target

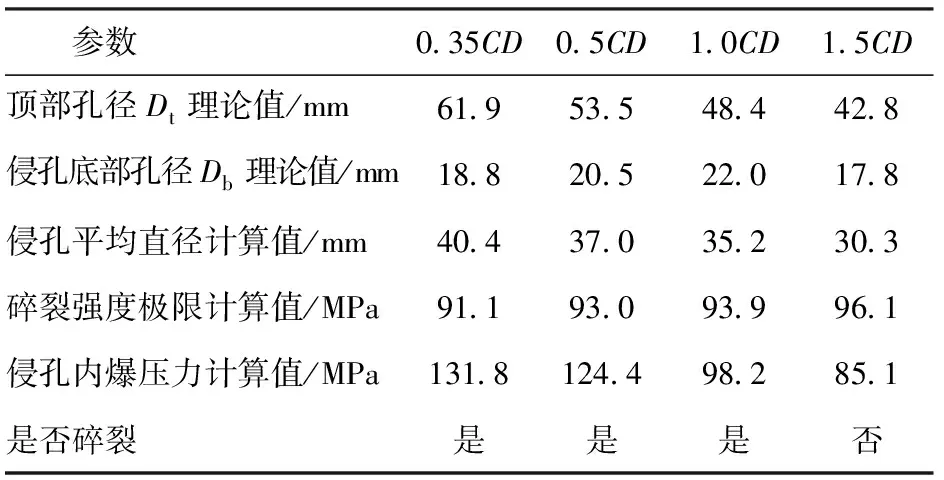
表4 不同炸高下钢靶侵孔直径与碎裂强度极限计算Table 4 Calculation of the penetration hole diameter and ultimate fracture strength under different stand-offs

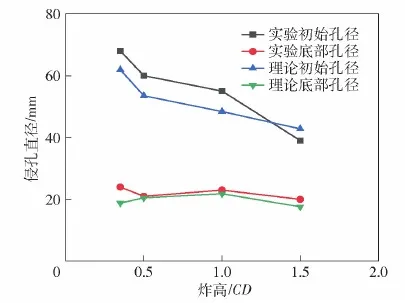
图13 活性射流侵孔理论计算值与实验结果对比Fig.13 Comparison of experimental and calculated results regarding hole diameter

假设活性射流在钢靶上产生的侵孔为理想梯形，如图14所示，则侵孔平均直径Da为

(34)

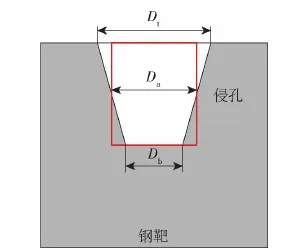
图14 侵孔平均直径Fig.14 Average perforation diameter

对不同炸高条件下活性射流侵爆钢靶产生的侵孔平均直径、射流侵彻后钢靶碎裂强度极限、侵孔内压力进行计算，结果列于表4。由表4可见：当炸高为0.35CD时，活性射流侵彻对钢靶产生一定侵彻深度和较大侵孔直径，钢靶碎裂强度极限降低，为91.1 MPa，而后到达反应延迟时间τ，随入侵孔内的有效活性材料发生剧烈化学反应，产生的内爆压力约为131.8 MPa，大于钢靶碎裂强度极限，因此在钢靶上产生多条径向贯穿裂纹；随着炸高增大，活性聚能装药对钢靶侵孔直径逐渐减小，钢靶碎裂强度极限逐渐增高，且由于随进侵孔内有效活性材料质量减少，在侵孔内产生压力降低，钢靶碎裂程度逐渐呈下降趋势；当炸高增加至1.5CD时，活性射流作用钢靶产生的平均侵孔直径为30.3 mm，钢靶碎裂强度极限上升至96.1 MPa，到达反应延迟时间时活性射流随进有效质量为16.2 g，在侵孔内仅能产生85.1 MPa的压力，无法造成钢靶上径向裂纹的产生。