“四种意识”巧解力学计算题
2023-03-20甘肃省庆阳市陇东学院附属中学张金龙慕雪利
■甘肃省庆阳市陇东学院附属中学 张金龙 慕雪利
分析近几年的高考物理试题可以发现,力学计算题的鲜明特色在于“组合”。深入挖掘力学计算题的内在规律能够明确,要想顺利求解这类试题,就必须具备“元素组合”“思想组合”“观点组合”“步骤组合”这四种意识,将其化繁为简、化整为零、逐个击破。
一、“元素组合”意识
力学计算题多是一体多段、两体多段,甚至多体多段等多元素构成的综合性题目。试题中常出现的“元素组合”如图1所示。

图1
力学计算题变化多样,但大多数是对如图1所示“元素组合”框架图中各种情境的排列组合。阅读题目时要厘清它的元素组合,建立模型,找到似曾相识的感觉,克服对新题、难题的心理障碍。
例1如图2所示,粗糙水平轨道AB与竖直光滑半圆形轨道BC在B点平滑连接,轨道半径R=1.025 m,木板DE借助某装置固定在竖直平面内,木板DE平面与水平面之间的夹角θ=53°,ED的延长线恰好通过B点,水平轨道AB上的P点处有一弹射装置,P、B两点之间的距离l=0.5 m。现将质量m2=1 kg的小球b放在B点,利用弹射装置将质量m1=0.5 kg的小球a弹出,a、b两小球在B点发生弹性碰撞后,小球b经半圆形轨道BC后恰好垂直打在木板DE平面上的Q点,已知小球a与水平轨道AB之间的动摩擦因数μ=,取重力加速度g=10 m/s2,sin 53°=0.8,cos 53°=0.6。求:
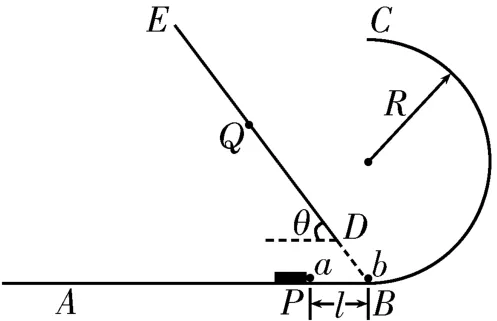
图2
(1)小球b从C点运动到Q点所用的时间t。
(2)弹射装置内最初状态下储存的弹性势能Ep。
元素组合:a、b两小球+水平面上的粗糙轨道AB+竖直面内的光滑半圆形轨道BC+竖直面内的倾斜木板DE+BC轨道上的圆周运动+恒力+平抛运动。
解析:(1)小球b从C点运动到Q点的过程中做平抛运动,设小球b在C点时的速度为vC,根据平抛运动规律可知,在水平方向上有x=vxt,vx=vC,在竖直方向上有y=,根据几何关系得tanθ=,解得t=0.3 s,vC=4 m/s。
(2)小球b从B点运动到C点的过程中,设小球b在B点时的速度为vB,根据机械能守恒定律得2R,解得小球a、b在B点发生弹性碰撞的过程中,设小球a在碰撞前后的速度分别为v1和v1',根据动量守恒定律得m1v1=m1v1'+m2vB,根据机械能守恒定律得解得。小球a从P点运动到B点的过程中,根据功能关系得μm1gl,解得Ep=33 J。
二、“思想组合”意识
一道经典的力学计算题宛如一个精彩的物理故事,处处蕴含着物理世界“平衡”与“守恒”这两种核心思想。求解力学计算题应牢牢抓住这两种思想,构建如图3所示的“思想组合”框架图。
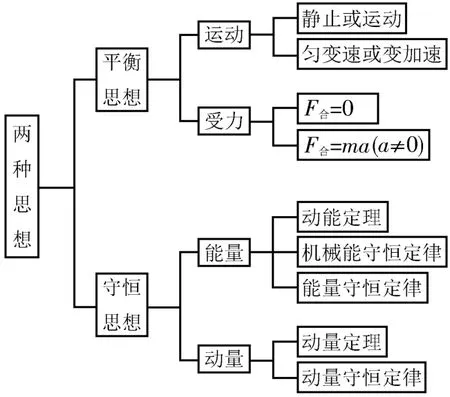
图3
平衡思想体现出对运动分析和受力分析的重视。运动分析与受力分析可以互为前提,也可以互为因果。如果考查运动分析,那么物体保持静止或匀速直线运动是处于平衡状态,物体做其他运动是处于不平衡状态。类似的,如果考查受力分析,那么也可以分为两种情况,即F合=0或F合=ma(a≠0)。当F合=0时物体受力平衡,当物体受力满足牛顿第二定律F合=ma(a≠0)时物体处于受力不平衡的各种情形。若想更具体些,则应追问物体是处于稳态平衡状态还是动态平衡状态,考查的是平衡位置还是平衡状态等。
高中阶段的物理守恒思想主要反映的是能量与动量恒定不变的规律。能量与动量虽不同于运动与受力,但不同的能量形式对应不同的运动形式,不同的动量形式也对应不同的受力形式,因此在本质上能量与动量都来源于物体运动情况与受力规律的推演,利用守恒思想求解物理问题是运动分析与受力分析的延伸。
例2质量为m木、长度为d的木块放在光滑的水平面上,木块的右边有一个销钉把木块挡住,使木块不能向右滑动,质量为m的子弹以水平速度v0按如图4所示的方向射入木块,刚好能将木块射穿。现将销钉拔去,使木块能在水平面上自由滑动,而子弹仍以初速度v0射入静止的木块,求:
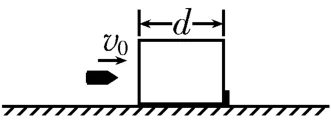
图4
(1)子弹射入木块的深度是多少?
(2)从子弹开始进入木块到子弹相对木块静止的过程中,木块的位移是多少?
(3)在这一过程中产生的内能是多少?
思想组合:
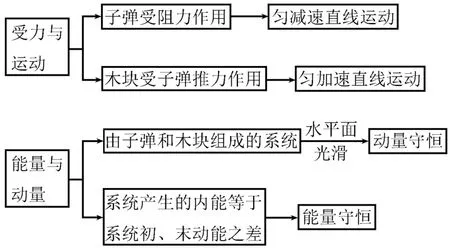
解析:(1)设子弹所受阻力为f,则木块不动时有,木块在光滑水平面上滑动时,由子弹与木块组成的系统动量守恒,则mv0=(m+m木)v,对子弹有v20-v2=,对木块有,子弹射入木块的深度l=x1-x2,联立以上各式解得l=
三、“观点组合”意识
求解力学计算题主要使用三种观点:受力与运动的观点、做功与能量转移的观点、冲量与动量的观点。这三种观点组成了一个庞大的知识体系,仅公式就多达几十个,不单学习时难以记忆,解题时也容易混淆。为获得顺畅的思路,可删繁就简,整理成如图5所示的“观点组合”框架图。

图5
动力观点的特征是涉及加速度的确定,主要用于解决物体受力情况与物体运动状态的关系。已知受力求运动,从力F的表达式F合=0或F合=ma写起,进而得出运动参数x、v、t或θ、ω、t;已知运动求受力,则从x、v、t或θ、ω、t表示的各种运动规律写起,反向得出物体所受的力F。
功能观点主要用于解决不涉及时间的问题。若不涉及时间,则通常使用动能定理列式求解;若不涉及时间又需研究能量,则优先使用能量守恒定律列式求解。
若研究的问题涉及时间,则使用动量观点中的动量定理列式可以简化计算。动量守恒定律的适用范围比牛顿第二定律更为广泛。遇到多体问题时,选择合适的系统,运用动量守恒定律列式求解,往往更加便捷。
例3如图6所示,长木板B的质量m2=1 kg,静置在粗糙的水平地面上,质量m3=1 kg的物块C(可视为质点)放在长木板的最右端。质量m1=0.5 kg的物块A从距离长木板B左侧l=9.5 m 处,以速度v0=10 m/s朝着长木板B运动。一段时间后物块A与长木板B发生弹性正碰(时间极短),之后三者发生相对运动,整个过程中物块C始终在长木板B上。已知物块A、长木板B与地面之间的动摩擦因数均为μ1=0.1,物块C与长木板B之间的动摩擦因数μ2=0.2,物块C与长木板B之间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2,求:
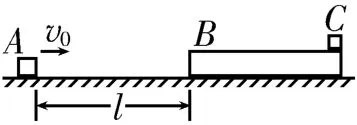
图6
(1)碰后瞬间物块A和长木板B的速度。
(2)长木板B的最小长度和最终物块A离长木板B左侧的距离。
观点组合:
解析:(1)设物块A与长木板B碰撞前的瞬时速度为v,根据动能定理得-μ1m1gl=解得v=9 m/s。物块A与长木板B发生弹性碰撞,假设二者碰撞后的瞬时速度分别为v1、v2,根据动量守恒定律得m1v=m1v1+m2v2,根据机械能守恒定律得解得v1=-3 m/s(方向向左),v2=6 m/s(方向向右)。
(2)碰撞后长木板B做减速运动,物块C做加速运动,长木板B和物块C达到共同速度之前,根据牛顿第二定律,对长木板B有-μ1(m2+m3)g-μ2m3g=m2a1,对物块C有μ2m3g=m3a2,解得a1=-4 m/s2(方向向左),a2=2 m/s2(方向向右)。设从碰撞后到二者达到共同速度经历的时间为t,则v2+a1t=a2t,长木板B的最小长度dmin=解得t=1 s,dmin=3 m。长木板B与物块C达到共同速度之后,因为μ1<μ2,所以二者一起做减速运动至停下,设其加速度为a3,根据牛顿第二定律得-μ1(m2+m3)g=(m2+m3)a3,整个过程中长木板B向右的位移,解得a3=-1 m/s2(方向向左),xB=6 m。物块A与长木板B碰撞后,物块A向左做减速运动的加速度也为a3,向左的位移解得xA=4.5 m。因此最终物块A离长木板B左侧的距离为xA+xB=10.5 m。
四、“步骤组合”意识
部分同学在求解力学计算题时,即使面对比较熟悉的物理情境,仍会不知道如何表述。为了厘清解题思路,可以尝试使用如图7所示的四个步骤来书写。
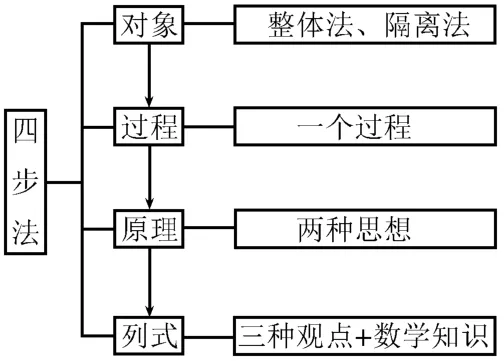
图7
例4如图8所示,一竖直光滑绝缘的管内有一劲度系数为k的绝缘弹簧,其下端固定在管底,上端与一质量为m、带电荷量为+q的小球A相连,整个空间存在一竖直向上的匀强电场,小球A静止时弹簧恰为原长,另一质量也为m且不带电的绝缘小球B从距小球A上方为x0的P点由静止开始下落,与小球A发生碰撞后一起向下运动,全过程中小球A的电荷量不发生变化,重力加速度为g。
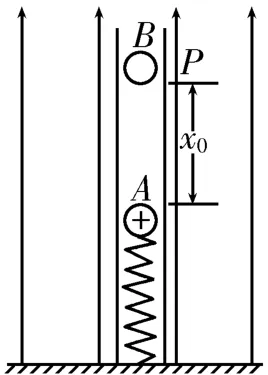
图8
(1)若x0已知,试求小球B与A碰撞过程中损失的机械能。
(2)若x0未知,且小球B与A运动到最高点时恰未分离,试求小球A、B运动到最高点时弹簧的形变量。
(3)在满足(2)问的情况下,试求小球A、B在运动过程中的最大速度。
步骤组合:
解析:(1)设匀强电场的电场强度为E,碰撞前小球A静止时有qE=mg,解得E=设小球B与A碰撞前的瞬时速度为v0,根据机械能守恒定律得解得设小球B与A碰撞后达到的共同速度为v1,根据动量守恒定律得mv0=2mv1,解得小球B与A碰撞过程中损失的机械能2mv21,若x0已知,则
(2)小球A、B一起向上运动至最高点时恰不分离,说明此时小球A、B的加速度相等,且它们之间的弹力为零。设此时弹簧的伸长量为x1,则对小球B有mg=ma,对小球A有mg+kx1-qE=ma,解得
(3)小球A、B一起向下运动所受合外力为零时,具有最大速度vmax。设此时弹簧的压缩量为x2,则2mg-(qE+kx2)=0,解得x1=x2说明小球A、B在两对应位置时弹簧的弹性势能相等。在小球A、B从获得最大速度处运动至最高点处的过程中,根据能量守恒定律得(2mg-qE)·,解得
