差异分析策略在2022年新高考数学试题中的应用探究*

杨宇佳 苏洪雨

(华南师范大学数学科学学院 510631)

1 背景

*本文系国家教育考试科研规划2021年度重点课题“面向教考衔接的新时代高考数学内容改革研究”(GJK2021008)、广东省高等教育教学改革项目“新师范课程‘数学解题研究’线上线下混合教学设计研究”(粤教高函〔2020〕20号)的阶段性研究成果.

2022年新高考试题深化基础性考查，注重数学的本质与创造性思维，深入考查核心素养和关键能力[1]，因此要想学好数学，领会精髓，必须要掌握最基础的两个能力：精确计算和严谨证明.美国著名教育家波利亚曾说过：掌握数学就意味着要善于解题.而数学题目是千奇百怪、变化莫测的，当解题遇到瓶颈时，到底应当如何应对？利用解题技巧，只能对固定的某类问题进行套路化的解题程序，仍处于解题的识别、模仿等低能力层级，是新高考正要逐步淡化的内容；而仅仅了解解题思想，对解题的方向指引也较低[2].因此需要一个真正能在解题时提供思路，但又不是某种固定题型的套路化程序的方法.实际上这就是解题策略：当解题陷入困境时，能利用某种有效的解题策略灵活调动知识，获得相应的解题路径.

基于上述背景，对差异分析这个解题策略进行研究，选取2022年新高考数学试题中的部分题目，利用差异分析策略逐一进行探究，领会差异分析在数学解题过程中的作用和效果.

2 解题中的差异分析策略

通过分析题目给出的条件与所要求的结论之间的异同，并不断减少目标差来完成解题的策略，称为差异分析策略[3].运用差异分析可以同时考虑“从哪里入手”和“向哪里前进”这两个关键问题，通过灵活调动已经内化的相关知识点，找到解题方法或简化解题过程.

以下是解题过程中差异分析策略的具体步骤：

(1)寻找题目给出的条件与所要求的结论中出现的特征,如：数量特征(元素个数、字母的系数或指数等)、关系特征(大于或等于、平行或垂直等)和位置特征等；

(2)寻找条件与结论中的特征差异，即目标差；

(3)灵活调动已掌握的知识点，主动作出尝试减少目标差的反应，向着减少目标差的方向前进，完成解题.

使用差异分析进行解题时，注意不能盲目地作出反应，减少目标差的调节要反复多次发挥作用，使得目标差的减少可以积累起来，这样的行为才是有效果的.

3 差异分析策略在解新高考试题中的应用

3.1 三角恒等变换

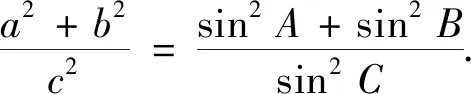
三角函数的化简、证明和求值变换是学习的一大难点，它对思维的灵活性和逻辑推理、数学运算核心素养有较高要求.这类题型本应是较易得分的题目，但很多考生在处理条件时，因为方向不对导致没有思路或屡屡碰壁，在考场上耗费大量时间.通过这道新高考的三角函数例题可以发现，解题的关键在于掌握三角函数的公式，当没有思路或方向错误时，可以考虑对角、函数名和运算结构进行差异分析，再灵活运用公式去建立差异间的联系，并不断减少这样的目标差[4].在此过程中，如果熟悉变换方法，把握变换方向，并恰当运用变换技巧，就能灵敏地应用差异分析策略来解决此类问题.

3.2 不等式的证明

例2(2022新高考II卷12题)若实数x,y满足x2+y2-xy=1，则( ).

A．x+y<1 B．x+y≥-2

C．x2+y2≤2 D．x2+y2≥1

分析 寻求已知式x2+y2-xy=1和未知式x+y,x2+y2之间的差异，减少它们之间的目标差，构建联系.

观察x2+y2-xy=1和x+y之间的差异，发现完全平方公式(x+y)2=x2+y2+2xy与之相关，因此不妨尝试将已知式转化为完全平方公式进行观察，即x2+y2=1+xy⟹(x+y)2=1+3xy，显然当x,y>0时x+y>1，故A错误.

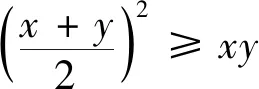
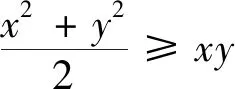
由于x2+y2=1+xy，选项D要判断x2+y2与1之间的大小关系，要减少二者差异，不妨设xy<0，此时x2+y2显然小于1，故D错误.

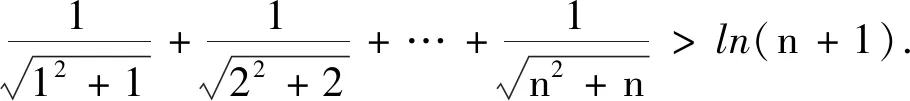
分析 观察不等号左边与右边ln(n+1)的差异，尝试作出一些减少目标差的反应，通过逐步消除差异进行求解.

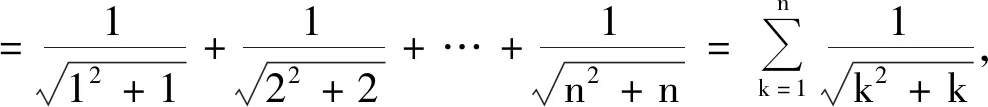
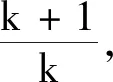
不等式的证明是通过逻辑推理来判断不等式的变量在允许的取值范围内使得不等式成立.其证明思路开阔，方法灵活，技巧性强，往往需要运用创造性思维和较高的运算技巧.通过这道新高考中的不等式例题可以发现，不等式的证明可以考虑从不等号两边的式子入手，观察它们之间的差异，借助已有的函数、数列、导数等相关知识点，减少它们之间的不同.这一步对不同模块的知识掌握和调动能力有一定要求，较复杂的不等式的证明，甚至还需要综合运用多种方法和技巧来完成.当目标差被一步步减少时，不等式的结论也会逐步清晰.

3.3 恒等式证明

例4(2022天津卷18题)设{an}是等差数列，{bn}是等比数列，且a1=b1=a2-b2=a3-b3=1．设{an}的前n项和为Sn，求证：(Sn+1+an+1)bn=Sn+1bn+1-Snbn.

分析 根据题目可得an=2n-1,bn=2n-1.要证(Sn+1+an+1)bn=Sn+1bn+1-Snbn①,①式中含有{an}的前n项和Sn，而目前仅知an,bn的通项公式，要想减少二者差异，需找到Sn与an间的联系：an=Sn-Sn-1(n>1)或an+1=Sn+1-Sn②.观察①式和②式之间的差异：①式中每项都存在一个与bn相关的式子，而②式没有，故作出减少目标差的反应，尝试让bn不再出现，可将①式表达为(Sn+1+an+1)bn=Sn+1·2bn-Snbn，由于bn≠0，就可以在等式两边消去bn，这时①式可表达为Sn+1+an+1=2Sn+1-Sn，实际上，Sn+1-Sn=an+1恰好为已知的②式，故原式得证.

恒等式的证明分为一般恒等式的证明和条件恒等式证明.对于一般恒等式的证明，常常通过恒等变形从一边证到另一边，或证两边都等于同一个数或式；要证明条件恒等式，可以从条件入手推出结论，或从结论入手构造条件，还可将条件和结论同时改变，以创造运用条件的机会.这种等式的计算或证明，是代数式部分的综合应用.差异分析能够给出一种直截了当的通性通法.例4本质上是一个条件恒等式，可以利用差异分析，只需知道通项和前n项和之间的关系就能得到解法.可见，如果借助差异分析策略来解决恒等式问题，当等号两边的目标差明晰时，那么向着减少目标差的方向逐步前进，问题即可获解.

4 差异分析策略的应用反思

通过对以上试题的探究可知，新高考的题目突出对基本概念、原理的考查，强调知识间的内在联系，注重本原性方法，淡化解题技巧，强调通性通法的综合运用.掌握必要的解题策略能有效促进解题者将知识和方法内化为自身的知识结构，借助差异分析的解题策略，能更高效地解决一些三角恒等变换、恒等式或不等式的证明问题.未来的考试中可能会出现更多的“证明问题”，当解题陷入困境时，可以尝试运用差异分析策略，从表象出发，寻求数学问题的本质联系，借助这种联系消除差异，将条件化为结论[5].需要注意的是，在应用差异分析策略时，针对具体的问题，需要不断变换思维角度，全方位联系已有知识，多角度思考问题，才能更快形成“寻找差异、发现差异、消除差异”的解题方案[6]，更进一步发展数学核心素养和关键能力.