解读“变”、思考“教”、引导“学”、研究“考”——人教A版新教材“导数”的解读与思考

盛 姗

(浙江金华第一中学 321015)

2020年9月，依据《普通高中数学课程标准(2017年版)》编写的人教A版普通高中数学教科书(以下简称“新教材”)正式启用.新教材在内容体系、逻辑结构、例习题等方面与2007年版普通高中课程标准实验教科书(以下简称“旧教材”)相比有诸多变化.使用新教材时，要比较新旧教材，了解它们之间的传承与变化；要分析它们的差异，对于修改和增加的内容应揣摩新教材的编写意图；及时转变教学理念，思考如何进行有效教学，坚持“在继承中前行，在改革中完善”[1]，最终落实数学学科核心素养.本文以选择性必修第二册“导数”一章为例，进行新教材导读以及新旧教材比较.

1 关于导数

1.1 导数的历史

·最早的极限思想

早在魏晋时期，刘徽的“割圆术”(割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣)就体现了“逼近”的极限思想，奠定了微积分理论基础.

·导数的起源

大约在1629年，法国数学家费马研究了作曲线的切线和求函数极值的方法，作切线时构造了差分f(A+E)-f(A)，里面的因子就是我们现在所说的导数f′(A).

·微积分的创立

17世纪，科学家们对物体运动的瞬时速度，求曲线的切线，求函数的最大(小)值，以及求长度、面积、重心等四类问题不断探索和研究，在此基础上，牛顿和莱布尼兹各自独立地创立了微积分[2].

1.2 导数的地位

导数是微积分的核心内容之一，是联系高等数学和初等数学的纽带；它定量地刻画了函数的局部变化，是研究函数性质的基本方法；同时它又是高中数学知识的一个重要交汇点，是联系多个章节内容以及解决相应问题的重要工具.导数的学习有利于提升学生的思维能力，使其以动态的、变化的、无限的变量数学观来研究数学，从而也有利于学好高中其他课程.

2 新旧教材比较与分析

新教材的编写思路是：借助两个具体实例，归纳出导数的概念及其几何意义之后，给出基本初等函数的导数公式，接着学习四则运算法则和复合函数的导数；最后利用导数研究函数的单调性、极值与最大(小)值等性质，感受导数在研究函数和解决实际问题中的作用．

2.1 整体比较分析

·教材内容的增减

新教材将旧教材第4—7节(“生活中的优化问题”“定积分的概念”“微积分基本定理”“定积分的简单应用”)等内容都删了.另外，新教材增加了“抛物线的切线的斜率”这个实例.

·小节划分变化

新教材将“导数的概念”和“导数的几何意义”以及“函数的极值”和“函数的最大(小)值”分别合并成一节；又将“四则运算法则”和“复合函数的导数”分开，各自成一节(具体见表1).

表1 新旧教材关于“导数”内容的对比

2.2 新旧教材的微观比较分析

·对导数的概念生成过程的处理

导数的概念非常抽象，而导数的几何意义涉及一般曲线的切线的概念，对学生来说是全新的，也是有一定难度的[3].新、旧教材均采用概念形成的方式来给出导数概念.所谓概念形成是指通过对典型丰富的实例进行反复感知、比较和抽象，以归纳的方式概括出本质属性而获得概念的形成[4].但是新、旧教材的处理方式还是有些差异的，具体见图1和图2.

图1 新教材导数概念生成过程

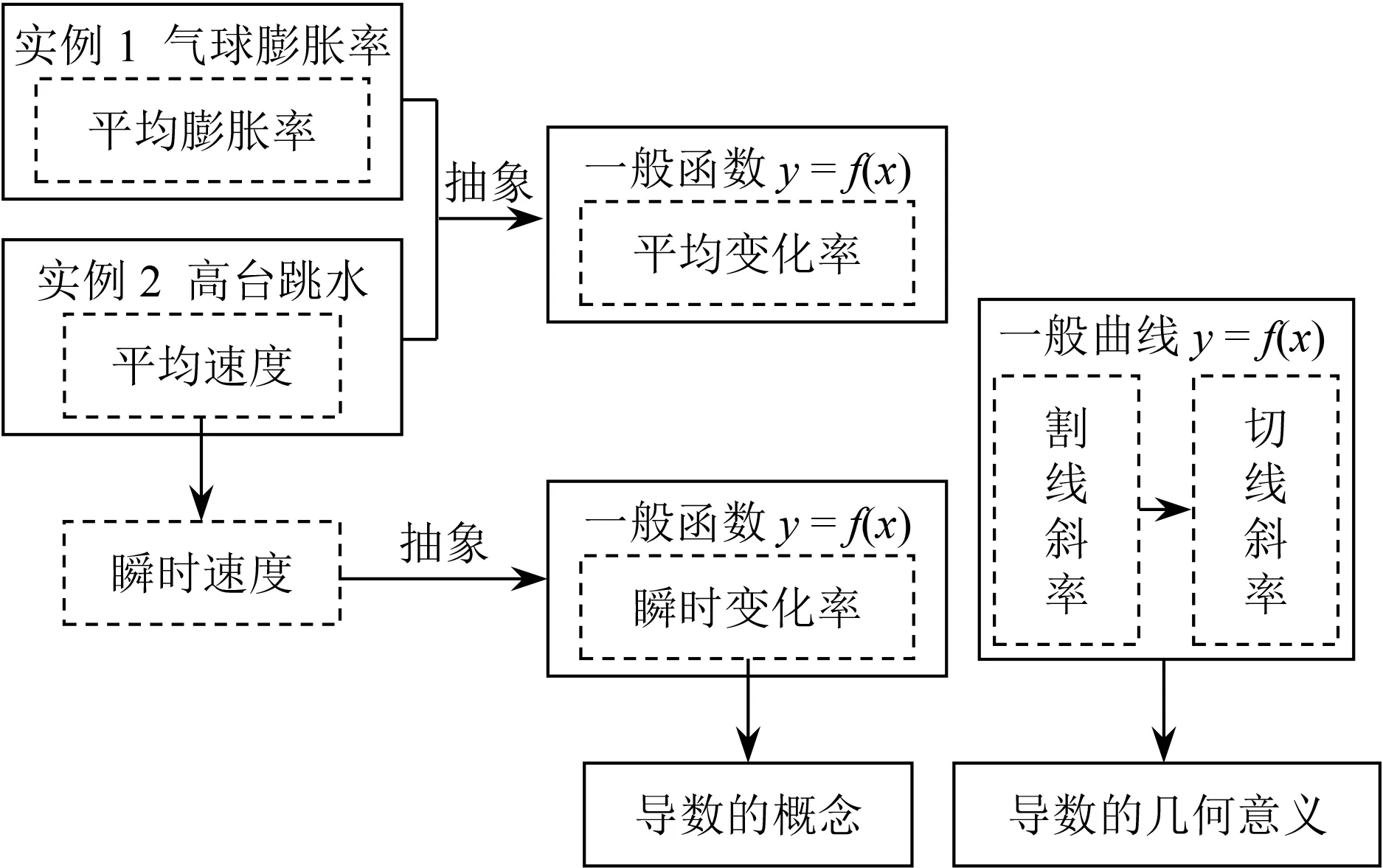
图2 旧教材导数概念生成过程

值得指出的是速度问题、曲线切线的斜率问题是导数概念产生过程中两个最为经典的实例.这样改变，既自然地呈现导数的物理意义和几何意义，又遵循了新教材主编李龙才副教授提出的“至少让学生经历4次由平均变化率过渡到瞬时变化率的过程”，助力学生初步理解导数的内涵．

·定积分内容的删减

旧教材中有三节内容是关于定积分的，但是新教材中已经不见其踪影.定积分涉及特别的认知方式，现属大学一年级数学知识，在高中阶段讲，学生的思维水平不够；再者定积分属了解内容，并且与高中其他内容关联甚少，为了减轻高中学生的负担，所以删去.

当然，定积分是微积分学中最基本的概念之一，并不是教材上没有就完全只字不提了，可以在“文献阅读与数学写作”中，组织学生搜集、阅读与微积分有关的资料及其对人类文明的贡献，从中感受理性精神．

·优化问题的重组

“生活中的优化问题”在旧教材中是单独成节的，但是新教材里看不见这个标题了.是真的删除了吗？事实上，里面的典型例题(饮料瓶大小对公司利润的影响)、重要习题和思想方法都被保留在了“函数的最大(小)值”一节里.这样重组的意图是什么？一方面，优化问题的题材来源于生活实际，利用导数解决实际问题是研究导数的最终意义所在，也是新高考重点考查的能力之一；另一方面，这些优化问题的本质就是利用导数研究函数的最大(小)值，是最大(小)值的实际应用.

·导数运算法则生成过程的变化

新教材遵循“实例探究→举例验证→归纳猜想→适度求证”的实施过程来组织求导法则的学习，过程自然合理、不突兀.从具体到抽象、从特殊到一般，符合学生的认知规律．

·函数增减快慢的处理

利用导数研究函数增减的快慢远比研究单调性抽象，这对学生来说是一个难点.新教材结合具体函数，让学生体会导数绝对值大小对函数图象增减快慢的影响，从而得出一般结论；既有形的直观又有数的严谨，较之旧教材仅从例题(注水容器水面高度问题)图象进行说明，学生更容易理解和掌握.这可能也是新教材删除该例题的原因.紧接着还安排了新例题，对上述结论进行应用和巩固，同时也为后面利用最值证明重要不等式埋下伏笔.

·例题、练习和习题的变化

一方面，新、旧教材在例题、练习和习题的数量上都有明显增加，特别是练习数量，是旧教材的两倍多，反映出新教材更注重教学的及时评价性.习题分为“复习巩固”“综合运用”和“拓广探索”三个层次，更为精准地定位习题的目标功能，供不同层次的学生选择使用.“复习巩固”和旧教材A组题量相当，“综合运用”和“拓广探索”题量接近旧教材B组的两倍，反映新教材更重视知识的综合运用和拓展，注重培养学生综合运用能力和数学探究能力.例题习题变化如图3(这里只对比导数概念、运算和应用的内容，如果一道题有n个独立小题，则计数为n).

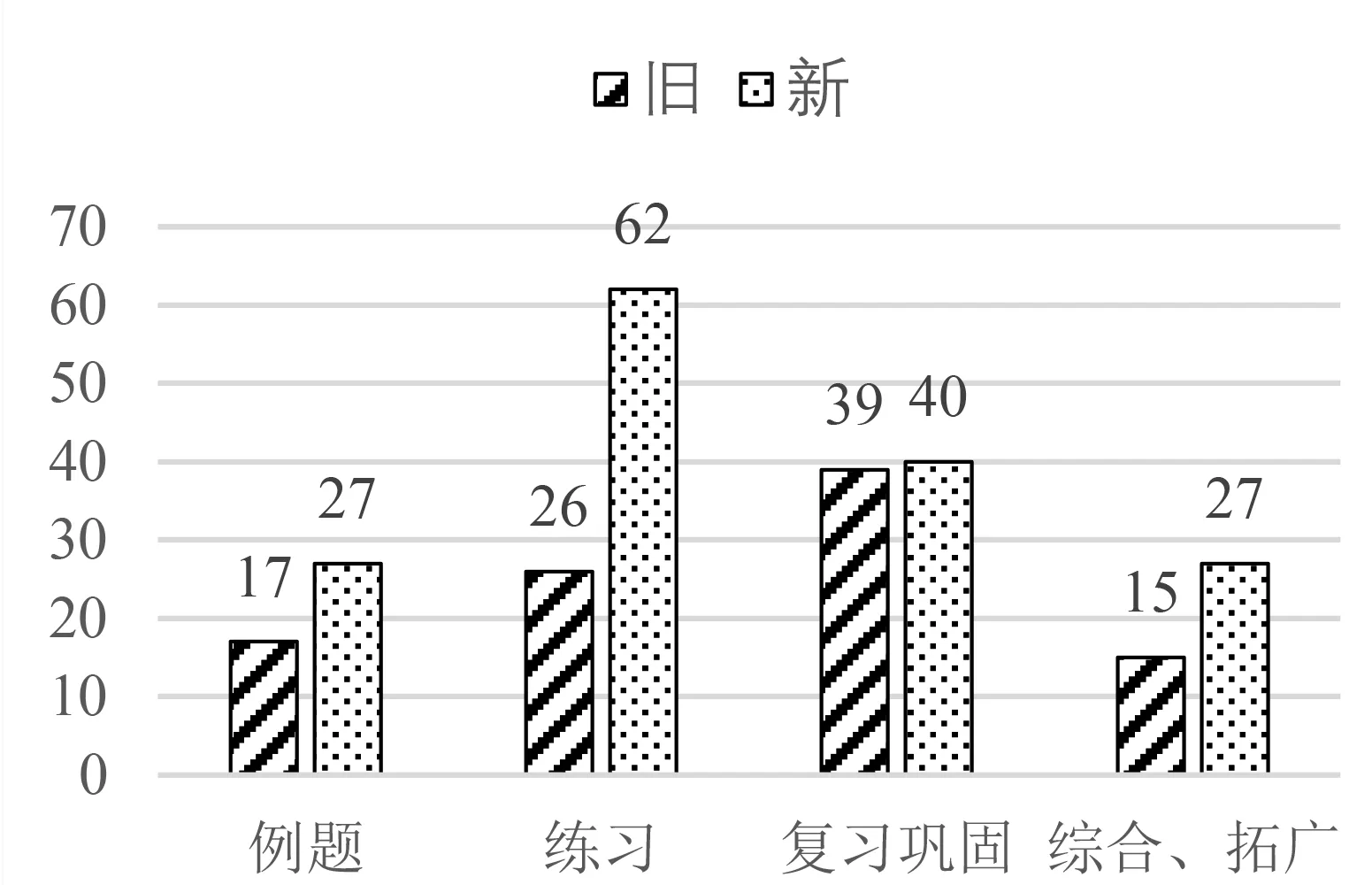
图3 例题、练习和习题的变化

另一方面，例题层次更丰富.新教材在各个知识节点后新增基础例题，体现公式、定理的应用，并给出示范，便于学生模仿和操练.配套练习数量的增加与之形成呼应，先基础后应用，丰富的例题层次使教材更具使用价值，也有利于引导学生重视课本例题和习题，同时也体现教材注重数学运算和逻辑推理素养的培养.

3 数据修正，彰显新教材的严谨性

·实例问题修正

高台跳水是本章一以贯之的例子，在新、旧教材中的地位都是不言而喻的.跳水函数刻画的是运动员(视为质点，新教材以“重心”替代)距离水面的相对高度与时间的关系，符合物理学中质点运动模型和等效替代法思维.修正后的跳水函数符合运动员起跳瞬间重心离高台(10 m)的高度约1 m(常数项为11)，也符合最高点时重心升高了1.176 m，比旧教材中“升高2.156 m”更符合实际(现实中一般运动员跳至最高点时重心离台面高度约为1.3m).

·“思考”栏函数数据的变化

新教材以函数引导学生思考复合函数的求导法则，并将其设计在了例题中.求导后内函数的导数没有被掩盖，强化复合函数的求导法则.

4 一点思考

基于上述对新旧教材“导数”部分的对比分析，我们建议在教学过程中，教师用好教材“教”，学生用好教材“学”，师生用好教材“接轨高考”.

4.1 顺应教材变化，用好教材“教”

教材是第一教学资源，是教师实施教学的主要材料.教学中应顺应教材变化，理解教材编写变化的意图，及时转变教学理念.课堂设计可以考虑问题链形式，引导的成分可以多一些；教学方式也可以适当转变，让学生思考的时间多一些.特别是导数概念的教学，课堂上尽量让学生充分地经历4次“逼近”过程，让学生参与概念产生的整个过程，追求概念的自然生成，培养学生的直观想象和数学抽象素养.

借助信息技术工具，助力数学课堂教学.高中数学大部分是动态数学，教学过程中尽可能多借助软件展示相关内容的运动变化过程，帮助学生更好地理解数学，培养学生的直观想象能力.例如本章中曲线的切线问题，教学过程中可以利用几何画板或者GeoGebra演示割线到切线的趋近过程，体会极限思想.

树立用教材教而不仅仅是教教材的意识.在教学中，以教材为蓝本，适时拓展教学内容.例如借助信息技术工具体会切线时，建议增加体验三次曲线f(x)=x3在点P1(0，0)和点P2(1，1)处的切线，让学生直观感受新定义下切线的各种情形——切线不是只能“切”过曲线，还可以是穿过曲线的；切线与曲线的公共点可以是多个的.把知识横向延伸、让思维纵向发展，使素养无声地渗透.

4.2 顺应教材变化，用好教材“学”

引导学生采用多样化的学习方式.学生课前的预习及课后的梳理都离不开教材，教材的可读性就显得很重要了.新教材增加了小节导言和一些过渡式语句，有助于学生明晰本节学习的必要性及研究的路径与方法；设置“探究”“观察”“思考”栏，给学生自学研究指明方向；还有很多旁白助力思考，“探究与发现”开拓学生视野.这些变化都体现新教材更适合学生自己阅读、自学和检测.引导学生好好研读教材，包括章引言和小结等，仔细思考教材中的每一个问题[5]，用好教材“学”.

4.3 顺应教材变化，思考高考走向

教材是高考命题的主要依据，我们需要重视新教材传达出来的新信息.历年高考的导数大题中，利用零点存在性定理解决较为复杂的函数零点问题时，寻找使函数值异号的两个端点往往是一个难点.对于“究竟能不能用变化趋势来刻画”一直存有争议.教材新增例题的解答过程就是用“趋近”来刻画“变化趋势”，从而画出函数的大致图象.这种“趋近”刻画，一方面和新教材全面渗透的“运动变化观点”与极限思想相吻合；另一方面也体现新教材在指导学生解决问题方面实操性更强，可有效帮助学生突破难点.

复杂的导数不等式，往往需要利用与对数和指数有关的重要不等式进行放缩.重要不等式以往只出现在习题中，而在新教材中它们除了在习题中仍被保留了下来外，在例题中也可见到它们的影子，而且安排的篇幅还不小.在“单调性”例题中得到不等式，又在学习了“最值”后给出了证明.这些都无疑在释放一个信号：重视教材，充分挖掘教材的价值.