两道上海高中自招平面几何题的解析与思考
2023-03-20李钟全
李钟全
(江苏省南京市中华中学 210019)
1 背景简介
上海高中自主招生考试是由上海各所高中自主命题的入学考试,主要为了招收学有特长和有潜力的学生.自主招生考试主要考查的是学科知识,有的学校还设置了面试环节.理科自招题型较为偏竞赛题,题目新颖且拓展性强,部分数学、物理题涉及高中内容,类似于某些城市的特长生招生考试.《普通高中数学课程标准(2017年版2020年修订)解读》中指出:在目前的高中数学中,几何与代数成为密切联系的整体,这是将“几何与代数”作为主线的主要原因.在小学、初中以及高中,需要学习很多图形,对这些图形可以从以下几个方面整体把握:几何图形分类、图形研究基本问题、研究图形基本思想方法、几何直观——形数结合[1].这些内容主要涉及平面向量、复数、立体几何模型、空间向量、解析几何等单元体系,而这些知识主要是与初中平面几何相联系展开研究,其中尤以圆为背景的问题居多.本文剖析以下两道典型试题.
2 典例分析
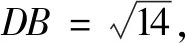
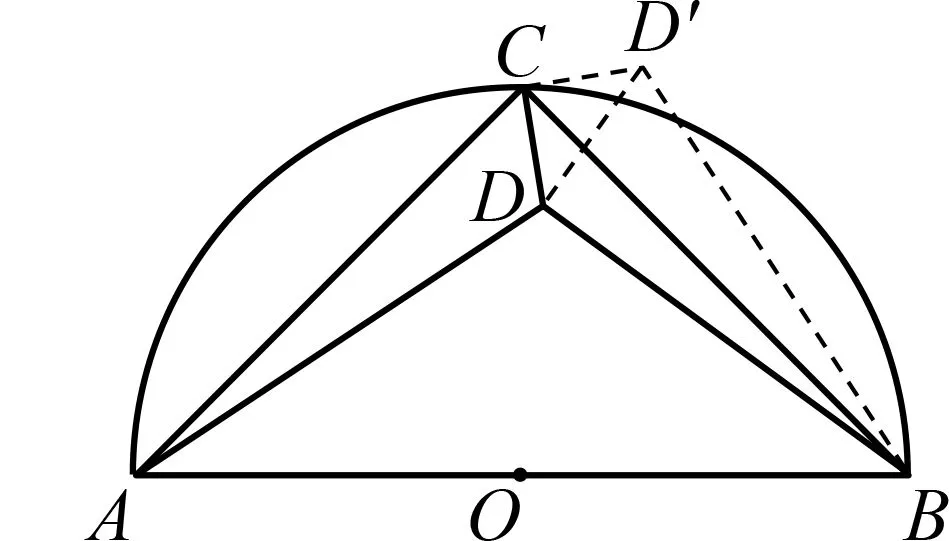
图1
分析对于这类图形具有对称性的问题,几何法与代数法应该都是行之有效的方法.先尝试用几何法分析:本题已知条件是三角形内一个点至三顶点的距离,类似于费马点问题中三个距离之和的最小值,故可以尝试运用证明费马点的方法,通过旋转三角形构造全等去求解.

说明 本题也可以将△CDB绕点C逆时针旋转90°,处理方法大致相同,读者可自己尝试.

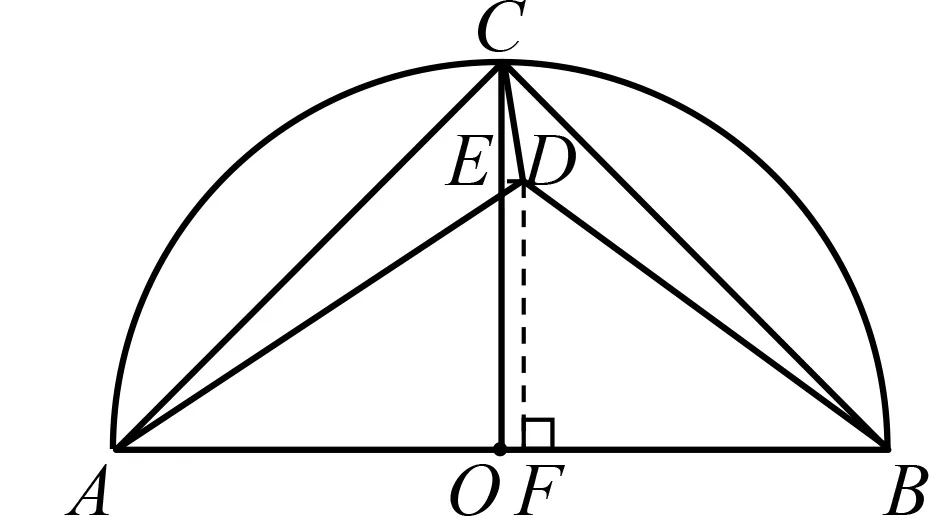
图2
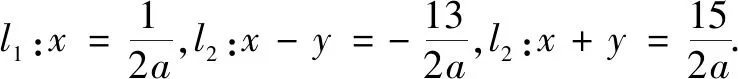

图3
点评本题是一道非常简约的初中平面几何问题,但非常巧妙地衔接了初、高中的数学知识和方法.其中几何法中渗透了射影几何中旋转变换的观点,非常巧妙.代数法运用勾股定理(余弦定理)将几何问题代数化,化为边的方程组,通过方程思想求解.最后结合平面几何相关定理,运用解析法巧妙地求出点的位置即为半径大小,体现解析几何的核心思想.本题的解法围绕圆这一核心内容触类旁通,体现数形结合、化归与转化等重要核心思想.本题非常巧妙地考查了学生的直观想象、数学运算等核心素养,对于一道初升高自主招生题来说具有较好的选拔功能.
思考在初中平面几何教学中教师会教授许多相似的构型,如顺相似、逆相似、旋转相似等.本题的解法1就是通过旋转相似的方法进行转化进而求解.平面几何教学应当重视基本图形和结构的教学,引导学生通过常见的平移、翻折、旋转等方法将复杂问题简单化,从而为高中几何的学习打下扎实的基础.
试题2如图4,冬奥会期间甲、乙两名滑冰运动员分别在圆形滑冰场的⊙O点A,B处,OB=20 m,OA=15 m,且OA⊥OB.乙以5 m/s的速度从点B沿着圆形滑冰场⊙O边顺时针方向滑行,在乙离开点B的同时,甲也以5 m/s的速度从点A沿着一条直线滑行,这条直线能使甲、乙在给定速度下最早相遇,则最早相遇的时间在( )(s)内[3].
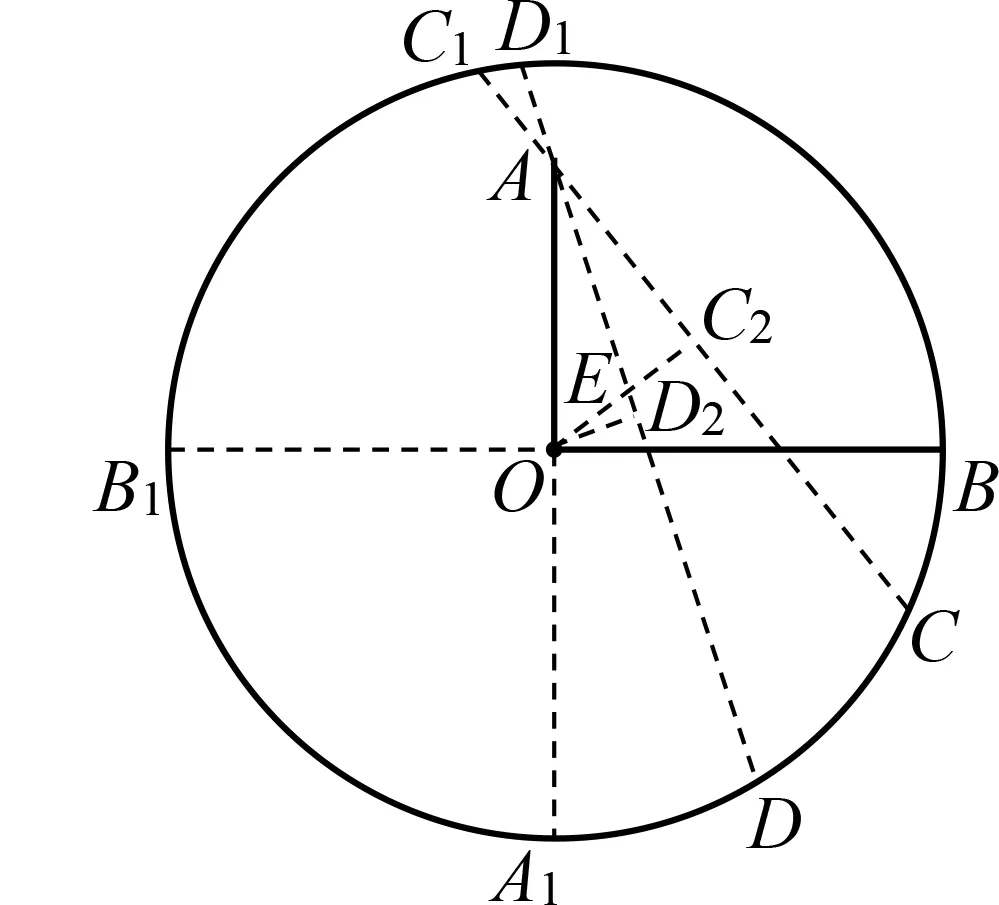
图4
A.(0,5) B.(5,6) C.(6,7) D.(7,10)

由相交弦定理知AC·AC1=AD·AD1,则(AC-AC1)2=(AC+AC1)2-4AC·AC1<(AD+AD1)2-4AD·AD1=(AD-AD1)2.显然AC-AC1>0,AD-AD1>0,故AC-AC1 ①+②得AC 由ABt≥AB=25,得t≥5,则乙至少滑行了25 m. 从而t<7,所以答案选C. 图5 点评本题是一道以圆为背景的上海高中自招题,学生易从图形角度分类讨论去发现范围.若运用高中方法,则渗透了高中数学重点考查的核心能力与思想方法——等价转化、函数与方程,而且作为证明过程也非常严谨,培养了学生的数学建模与逻辑推理等核心素养.可见多角度分析问题能够全面综合提升学生的学习能力及素养. 思考在教学中教师要带领学生熟悉与圆相关的基本模型和结论,如本题解法1中用到了相交弦定理.除此之外,我们还要让学生熟悉并常用圆幂定理(切割线定理等).解法2中运用的余弦定理和求导的方法是高中用于处理与图形有关的边角关系最值的常见做法,教师不能回避或淡化该类方法,而应选择和学生一起分析求解过程,为学生数学运算核心素养的提升提供必要的支持. 《中国高考评价体系》指出:高考考查特别重视“核心价值、学科素养、关键能力、必备知识”的“四层”考查内容,其中“关键能力”是支撑和反映学生专业素质特点的基本才能体现.关键能力中第三方面就是包含了所有重要思维能力的思维学习知识能力群,主要分为形象和抽象思维能力、综合归纳能力、演绎与推理能力、批判思维能力、辩证与统一综合能力等[4].在笔者看来,独立、有创造性地思考是首要能力,能够多视角、发散地、逆向地解决问题,就需要我们在解决问题时通过一题多解、正反分析论证、变式探究等途径加以落实.好的高考、自招和竞赛题就担负了如此的任务和功效,它要求学习者发掘新问题、使用新办法、处理新问题、得出新结果.学生若能不断反思总结自身解决新问题的过程,必然能达到中国高考评价体系的要求,以适应并达到高校通过强基计划、自主招生选拔优秀人才的需要. 初中平面几何的教学,要让学生明白什么是“严谨的科学”,什么是严密的逻辑推理.逻辑推理素养的培养要渗透、贯穿高中数学学习的全过程.在高中学习内容板块(函数、几何与代数、概率与统计、数学建模与探究)的概念、命题、证明等教学过程中,都应引导学生有逻辑地思考、表述、交流问题,不断全面提升学生的逻辑推理素养.
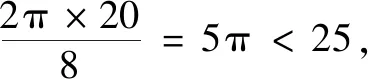
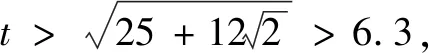
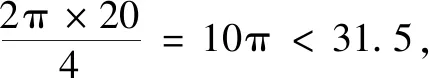

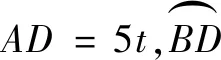

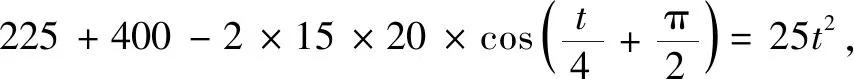
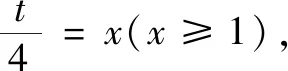
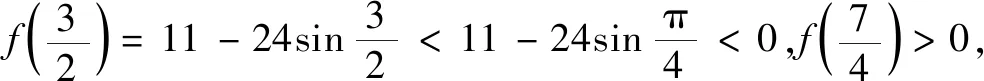
3 结束语
