压电复合材料结构的减振/致动性能优化
2023-03-20李志欣郑智伟黄修长
李志欣, 郑智伟, 黄修长
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
复合材料具有可设计性强、耐腐蚀、易成型等特点,目前已广泛应用于航空航天和海洋工业领域[1]。20世纪80年代中期,研究人员将传感器和致动器与复合材料相结合,制成纤维增强复合材料,有效提升了产品性能[2]。当纤维增强复合材料用于设计先进智能结构时,智能结构通过传感器感知外界扰动,并针对扰动信息驱动致动器作出相应动作,可应用于振动噪声控制、形状结构控制以及性能监测等[3]。压电材料具有正、逆压电效应,使得其既可做传感器,又可作致动器[4]。将压电材料通过嵌入或表面粘贴等方式与纤维增强复合材料结合,制备压电智能复合材料结构[5],可用于开发出超灵敏的传感器和致动器。
压电悬臂梁结构因其结构简单、设计灵活等优点被广泛研究[6]。压电悬臂梁模型包括分布式、单晶、双晶[7]与层合压电结构。分布式压电结构可以连接多个电路,主要用于振动控制。层合压电结构由于压电模块尺寸较大,相同激励下可产生较高电压,主要用于能量收集。压电层合梁结构的动力学模型通常基于Euler-Bernoulli梁理论[8]。Erturk等[9]推导了压电材料串联和并联的双晶悬臂配置,利用Euler-Bernoulli梁假设推导出了基础激励下悬臂梁弯曲变形的解析解。
压电元件与外部电路结合可应用于结构减振。Hagood等[10]首次建立了机电耦合方程对压电分流控制机理进行研究。目前常用的压电分流电路有电阻-电感型电路(RL)、电感-电容型电路(LC)以及负电容电路,均可用于结构振动控制[11],可用不动点法求得压电分流减振电路的最优电阻和最优电感。压电材料也广泛应用于结构致动[12]。Giddings等[13]评价了由宏观纤维压电致动器致动的双稳态碳纤维复合材料的结构性能,还研究了电压对偏转角度的影响。Hadjigeorgiou等[14]针对压电片致动模型使用遗传算法进行优化。Deng等[15]提出了一种行程范围较大的平面压电致动器。该致动器设计有四个均匀的压电传感器,每个传感器均可沿水平或竖直方向独立弯曲。
复合材料结构的铺层顺序和铺层角度会影响结构刚度,进而对动力学特性产生影响。Assarar等[16]通过数值模拟研究了混杂亚麻纤维-碳纤维不同铺层顺序、铺设角度对结构弯曲刚度和阻尼性能的影响;Madeira等[17]以层合板铺设层数、铺设角度和弹性阻尼层厚度为设计变量,以结构阻尼最大化、重量及材料成本最小化为目标,利用直接多目标搜索算法进行优化设计。李艳楠[18]利用有限元软件对带长圆孔碳纤维复合材料圆管进行数值仿真,分析了铺层角度和铺层顺序对圆管基频的影响。李根等[19]以层合板的临界屈曲载荷系数最大化为优化目标,基于改进模拟退火算法对结构铺层顺序和铺层角度进行优化,有效提高层合板的稳定性。
为提升压电复合材料结构的压电分流减振性能与致动性能,本文给出了相应的结构铺层设计建议,并在此基础上利用遗传算法分别对减振和致动性能进行了优化。该复合材料结构由碳纤维、玻璃纤维及压电纤维层组成。基于Euler-Bernoulli梁模型及Hamilton原理获得了结构的动力学方程。将压电层与外电路连接,对压电分流电路建模并推导了系统在单位激励下的末端位移频响函数;对比了六组对称铺设结构的减振性能与致动性能,明确了有助于提升减振和致动性能的复合材料结构铺层顺序;此外,为提升减振性能,利用遗传算法对压电片分布位置进行了优化及分析;为扩大致动角度,利用遗传算法对玻璃纤维和碳纤维的铺层角度进行了优化及分析。
1 复合材料结构机电耦合系统分析
图1为多层单向混合纤维复合基体与分布式压电片组合的压电复合结构示意图。将碳纤维、玻璃纤维和压电纤维结合构成结构基体,分布式压电片粘贴于基体上。其中,玻璃纤维构成绝缘层,碳纤维构成导电层。梁的全长为L。第i个压电片的位置为di。碳纤维、玻璃纤维和压电纤维的厚度分别为hc、hg、hp,铺层角度分别为θc、θg、θp。碳纤维、PZT纤维和玻璃纤维由下至上对称铺设,记为[C P G]s,下标s表示对称铺设。压电层合梁的材料为各向异性;纤维方向与x轴正方向的夹角为铺层角度,铺层角度和铺层顺序具有对称性。多层单向混杂纤维结构满足经典层合板假设[20]。

图1 压电层合梁结构示意图Fig.1 Diagram of the piezoelectric laminated beam structure
1.1 复合材料结构机电耦合系统建模
压电层合梁假设为Euler-Bernoulli悬臂梁,利用Hamilton原理对压电层合梁进行动力学建模

(1)
式中:Tk为动能;U为势能;We为电能;δW为外力所做虚功。
压电层合梁结构的横向位移用Rayleigh-Ritz法表示为:
(2)
式中:φr(x)是第r个弯曲模态振型函数;rr(t)是与时间有关的第r个广义模态坐标。电能We和虚功δW如下
(3)
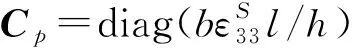
(4)


(5)
式中,cb为阻尼系数。动能Tk和势能U为
(6)
式中,M为压电层合梁结构的模态质量矩阵,它由基底模态质量矩阵Mb和分布式压电片模态质量矩阵Mp组成

(7)
式中:n为压电片的数量;下标b表示基体的相关特性;下标p表示分布式压电片的特性。ρ表示密度,b和h表示宽度和厚度。
模态刚度矩阵K为
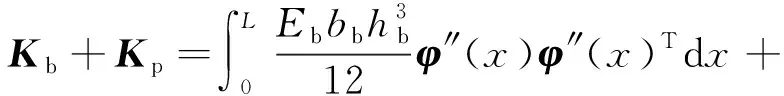
(8)
式中:Kb为基体模态刚度矩阵;Kp为粘贴在基体上的分布式压电片刚度矩阵。
传统分布式压电结构的基体为单一材料,而压电层合结构的基体由多层单向混合纤维材料组成。因此,基体的弯曲模量Eb需要通过EI/IH求解。IH=bbh3b/12为面积惯性矩;bb和hb是基体的长度和高度。EI为基体的弯曲刚度:
(9)
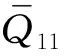
将式(3)和式(6)代入式(1),得到压电复合悬臂梁结构的机电耦合系统
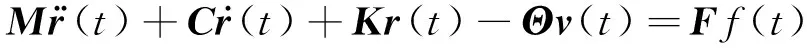
(10)
Θr(t)+Cpv(t)+q(t)=0
(11)
1.2 分流电路建模及系统响应分析
压电纤维层与RL电路串联,电路关系为

(12)
式中:q(t)为电荷向量;R和L分别为电阻向量和电感向量。
将式(12)代入式(10)和式(11)
(13)
(14)
w(L,t)为施加激励力时的位移响应,模态坐标和电荷以简谐形式代入式(13)和式(14),得出末端位移的频响函数为
(15)

1.2 复合材料结构模型验证
将复合结构固有频率推导结果与COMSOL计算结果对比以验证上述推导的正确性。压电复合悬臂梁结构见图1。叠层顺序设置为[C P G]s,铺层角度为[0 0 0]s。压电片的长度为20 mm,宽度为10 mm,厚度为0.2 mm。材料性能参数如表1所示,几何参数如表2所示。

表1 压电复合悬臂梁结构材料参数Tab.1 Material parameters of piezoelectric composite cantilever beam structure

表2 压电复合悬臂梁结构的几何参数Tab.2 Geometric parameters of piezoelectric composite cantilever beam structure
压电复合悬臂梁结构的振型如图2所示,对应固有频率如表3所示。悬臂梁结构响应主要由前4阶模态贡献[22],因此选择前四阶模态的理论计算结果与有限元仿真的固有频率结果进行对比。COMSOL中求解的自由度数为96 438,单元数为32 374。




图2 压电智能复合悬臂梁振型Fig.2 Modal shapes of the piezoelectric laminated beam structure

表3 智能压电复合悬臂梁结构前四阶固有频率Tab.3 First four order natural frequency of intelligent structure
MATLAB和COMSOL结果的相互验证,误差在可接受范围。
2 复合材料结构铺层顺序设计
本节针对复合材料结构的铺层顺序进行了设计。当结构材料和层数确定后,结构特性由铺层顺序和铺层角度决定。对铺层顺序和铺层角度同时优化时,由于优化变量过多,无法获得准确的最优解。因此,本章首先对铺层顺序对减振性能和致动性能的影响进行分析。
六层对称复合梁有六种排列方式,压电层分别位于结构内层、中层和外层,六种配置如图3所示,其中下标s表示对称铺设,复合结构中每层厚度均为0.2 mm。


图3 不同铺层顺序的六种横截面配置Fig.3 Six cross-sectional conFigurations with different stacking sequences
利用压电分流电路对结构进行减振,第j个压电片在第i阶模态下的最优电阻-电感表达式如下
(16)
(17)

六种不同配置的压电复合梁对第一阶模态的减振效果及其对应的RL电路参数值如表4所示。减振性能用|Hrl(f1)-H0(f1)|评估,f1表示结构的第一阶固有频率,Hrl为串联RL电路下的频响函数,H0为无电路下的频响函数。
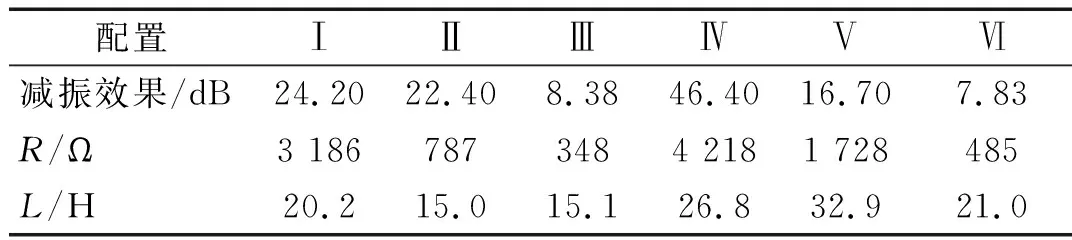
表4 第1阶模态的减振效果(dB)及对应的RL参数值Tab.4 Damping effect (dB) of the first-order mode and the corresponding RL values
从上述六种配置的第1阶模态减振性能来看,压电层在最外层时对第1阶模态的减振效果比在内部时效果好。这为减振压电层的布置提供了依据。
使用COMSOL软件对图3中六种横截面配置结构的致动效果进行仿真,得到单位电压下结构尖端的最大偏转位移如表5所示。
由表5可知,当压电层位于中间时,单位电压下的最大挠度最大。最终将致动部分的铺层顺序设定为[C P G]s,即图3中的Ⅱ型,该设计保证了结构的绝缘性。最终压电复合悬臂梁的功能设计为最外层压电层用作减振,内部压电层用作致动。最外层压电层可用于控制某阶结构振动模态,也可将压电层拆分为分布式压电片以进行多模态控制。

表5 静力分析下的致动效果Tab.5 Actuation effect under static analysis 单位:mm
3 复合材料结构性能优化及分析
3.1 压电分流减振性能优化及分析
复合结构的减振性能主要与压电片粘贴位置有关。压电片通常粘合在结构较高应变处以提升减振性能[23]。前三阶固有频率下基体应变如图4所示。可以看出基底前三阶模态中较高应变位置区间为[0,20]mm,[40,60]mm和[60,80]mm。基底的前三阶固有频率分别为 117.53 Hz、733.47 Hz和2 040.5 Hz。

图4 前三阶固有频率对应的应变云图Fig.4 The strain diagram at the first three natural frequencies
压电片长度为20 mm,将压电片布置于0、40 mm和60 mm处分别对前三阶模态进行减振。进一步使用遗传算法对分布式压电片的位置进行优化。为避免三个压电片产生干涉,三个压电片的位置变化区间为[0,10]mm、[30,40]mm、[60,75]mm。遗传算法以压电片的位置(xi)作为压电复合悬臂梁结构减振性能的优化变量,以一定频率范围内的频响函数绝对值之和最小为优化目标,优化方程如下
(18)
式中:H1是含RL电路时的频响函数;l是压电片的长度;f1、f2、f3分别代表压电复合悬臂梁结构的前三阶固有频率,压电片间不能产生干涉,压电片铺设位置不能超过压电悬臂梁的长度。遗传算法的迭代次数设置为60次,优化结果如图6所示。迭代适应度函数设计为每个参数下的频响函数绝对值之和。红色圆圈代表迭代期间的平均适应度,蓝色十字代表迭代期间的最佳适应度。当二者接近或相等时,遗传算法优化结果适用于所有样本,优化完成。遗传算法收敛时x1、x2、x3分别为0.007 7 mm、32.004 3 mm、68.018 5 mm,频响函数绝对值之和最小值为218 395 dB。
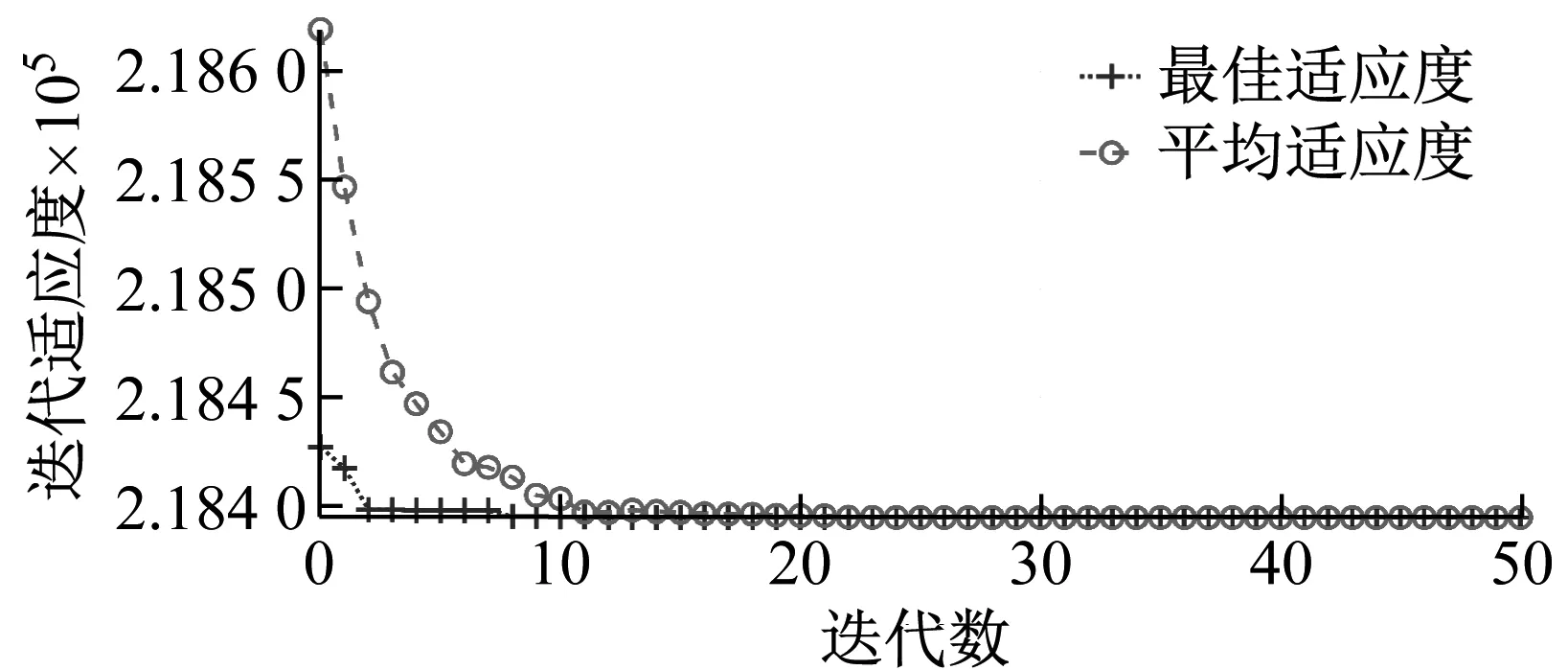
图5 遗传算法减振优化结果Fig.5 Result of the vibration damping optimization using the GA

图6 不同设置下压电层合悬臂梁结构的频响函数H1Fig.6 Transfer function H1 of the piezoelectric laminated cantilever beam structure at different settings
图6为将压电片粘合在高应变处与遗传算法优化的减振效果对比。虚线为无电路时的末端位移频响函数;点划线为压电片粘合于高应变位置时的频响函数;实线为遗传算法优化后的结果。优化后的前三阶模态振动峰值分别降低了 0.67 dB、0.77 dB、1.87 dB。改变分布式压电片的位置可以增强智能压电复合悬臂梁结构的减振效果。
三个压电片位置分别对结构减振性能的影响如图7所示。图7(a)、7(b)和7(c)分别为三个压电片对频响之和的影响,当分析其中某一压电片对整体频响的影响时,其余两个压电片固定于高应变位置。可以看出,当PZT1接近悬臂梁根部、PZT2位于30 mm、PZT3位于70 mm附近时,频响之和较小,减振性能较好,与遗传算法优化结果相吻合。
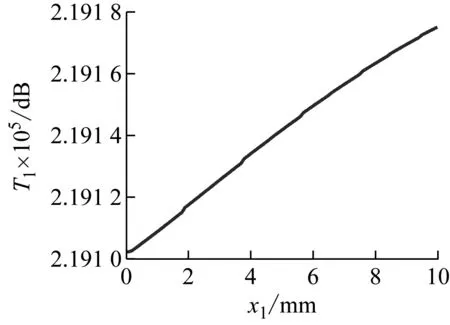
(a) PZT1对结构减振的影响

(b) PZT2对结构减振的影响

(c) PZT3对结构减振的影响图7 分布式压电片位置对减振性能的影响Fig.7 The effect of distributed piezoelectric patch positions on vibration damping
3.2 致动性能优化及分析
在对智能压电悬臂梁结构的减振性能优化后,利用遗传算法对致动性能进行优化。压电层用于致动时,可通过改变内部铺层的铺层角度来优化致动性能。压电纤维方向与x方向一致时,致动性能最好,因此,只需要对碳纤维和玻璃纤维的角度进行优化。选择100 V电压下压电复合悬臂梁结构的末端最大位移作为优化目标,以碳纤维角度θc和玻璃纤维角度θg为优化变量,遗传算法中的迭代次数设置为60次。碳纤维和玻璃纤维角度的变化范围为[0°,180°]。利用MATLAB程序调用COMSOL进行计算,遗传算法的优化结果如图8所示。图中圆圈为迭代期间的平均适应度,十字为迭代期间的最佳适应度。

图8 遗传算法致动优化结果Fig.8 Result of the actuation optimization using the GA
遗传算法收敛时θc和θg分别为90.001 5°、53.065 2°,末端位移的绝对值为0.968 215 mm。碳纤维和玻璃纤维角度变化对致动性能的影响如图9所示。当碳纤维的角度约为50°,玻璃纤维的角度约为90°时,致动性能最好。
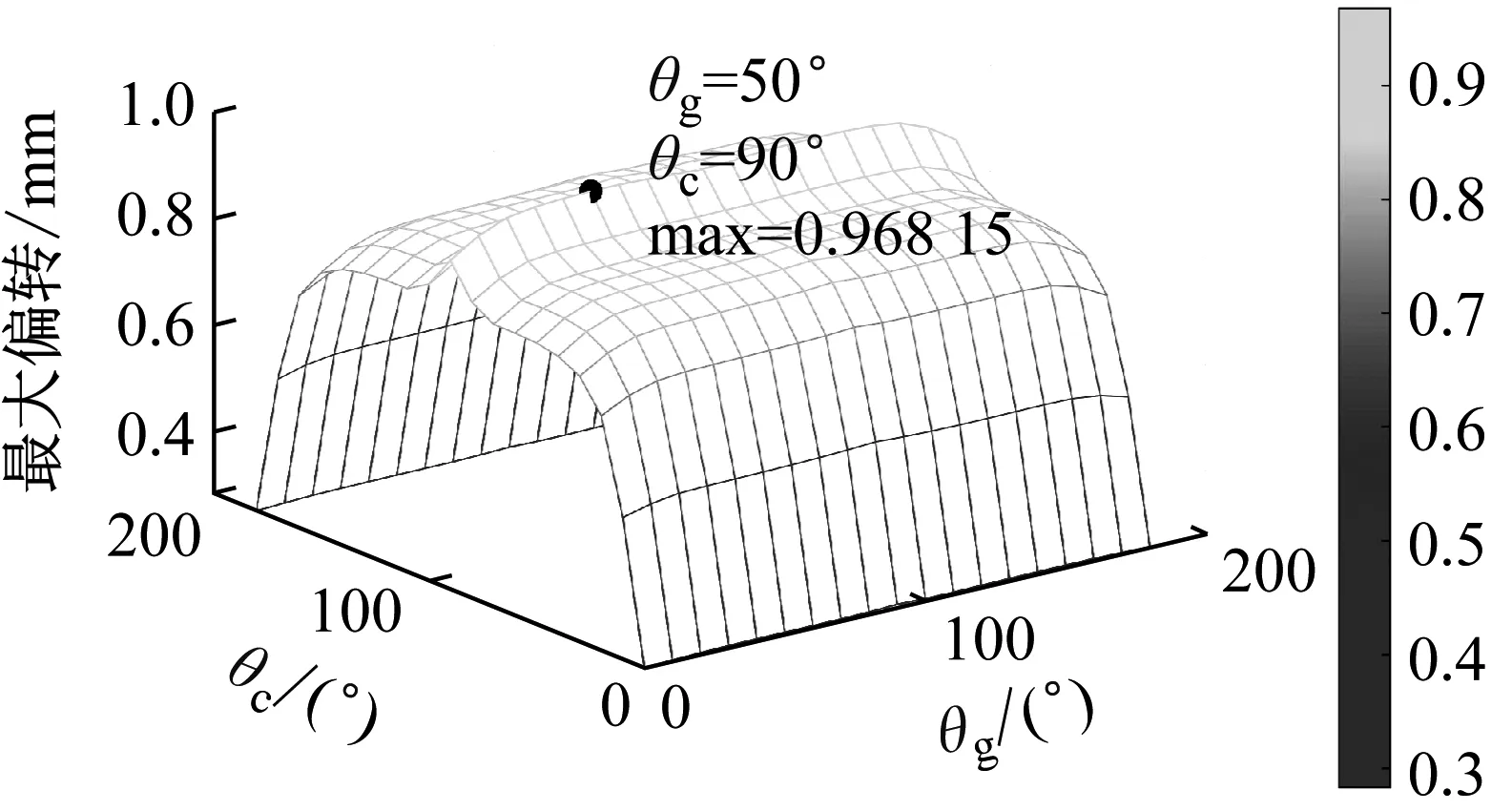
图9 铺层角度对致动的影响Fig.9 The effect of lay-up angle on actuation
4 结 论
本文针对压电复合悬臂梁结构的减振性能及致动性能进行分析优化,以Euler-Bernoulli梁模型为研究对象,利用Hamilton原理、经典层合板理论等推导了压电复合材料悬臂梁机电耦合动力学方程,对压电分流电路建模并得到了结构的末端位移频响函数。在此基础上对复合结构的减振及致动性能进行研究, 通过对比六组对称铺设的压电复合结构的减振与致动性能,明确了提升减振和致动性能的结构铺层顺序,即压电层位于最外层时减振性能较好,压电层位于中间层时致动性能较好。在减振方面,将最外层压电层拆分为分布式压电片,选取分布式压电片的位置为优化参数,利用遗传算法得到了比在高应变位置处粘贴压电片更好的减振性能。在致动方面,使用遗传算法对结构的碳纤维及玻璃纤维的铺层角度进行优化,增大了结构的偏转角度。本文所设计的复合结构具有更好的减振性能和更大的致动范围,在航空航天和船舶方面具有实用性。
