海底多跨管道流-固-土多场耦合试验研究
2023-03-20徐万海艾化楠马烨璇
徐万海, 艾化楠, 贾 昆, 马烨璇
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
海底管道是海洋油气开采输送的关键装备。由于海底复杂的地理条件,海流的冲蚀作用和管道自身的变形等因素影响,管道往往会产生悬跨现象。悬跨段在水流的作用下会出现交替脱落的旋涡,引发管道涡激振动,诱发管道结构的疲劳损伤,甚至破坏。实际工程中的悬跨段往往不是孤立出现的,多段悬跨时有发生。相邻悬跨段间的相互作用机理是海底管道涡激振动研究的重要内容。
多跨悬跨管道的研究起步较晚。Soni等[1]阐述了横流向涡激振动的能量在相邻悬跨段之间的传递效应,以及两跨间管土接触长度对悬跨管道涡激振动的影响。Koushan[2]提出预测悬跨段的涡激振动必须考虑跨肩处的复杂边界、多跨间的相互作用等因素。Sollund等[3-4]考虑轴向力影响及管线静态变形初始曲率,确立了相邻管跨对悬跨管道基本频率及模态应力的影响。结果表明:在评估波浪和海流引发管道结构疲劳损伤时不能忽略相邻跨的影响。Li等[5]采用铁木辛柯梁理论,考虑流体动力学效应,对悬跨管道模型进行了修正。Slinsby[6]应用尾流振子模型,选取了多种管土作用模型,分析了两跨管道在不同流速下的涡激振动响应特征,对比了多跨与单跨管道的最大响应幅值差异,证实了悬跨段数量是影响管道振动响应的重要因素。EI-Sayed等[7]基于变分迭代法,研究了多跨管道的动力特性和稳定性。结果表明:跨中支撑方式和刚度对管道固有频率有着显著影响。Li等[8]研究了非均匀多跨输油管道的结构模态特性,考虑了土体基础、附加质量和管道内流等因素。高喜峰等[9]基于两跨管道模型,通过尾流振子模型描述涡激振动流-固耦合问题,采用模态分析法揭示了边界土体刚度对振动的影响规律。
海床土体为海底悬跨管道提供支撑,对管道具有很强的约束作用。海床土体的特性决定了海底悬跨管道的固有频率,对管道涡激振动具有重要影响[10-12]。考虑到悬跨管道涡激振动的复杂性,顺流向振动和横流向振动耦合作用以及管土耦合作用均难以直接理论分析和数值模拟。因此,模型试验成为探究复杂条件下悬跨管道涡激振动特性的有效方法。Yang等[13]研究了管道间隙比对管道振动和局部冲刷的影响机制,发现振动与局部冲刷相互作用,最大振动幅值随初始间隙比增大而增大。李小超[14]利用方形土箱试验模拟土体边界,观测了土体端部支撑下的悬跨管道涡激振动响应,结果表明海床间隙对涡激振动的发生具有重要影响。谭鹏涛等[15]利用了波浪-水流-地震联合模拟试验系统,试验研究了波浪、水流和谐波地震荷载单独作用或联合作用时海底悬跨管道的动态响应特征。
目前,对于海底悬跨管道的试验研究远无法满足工程实际需求,尤其缺少多跨工况的试验数据,最核心的原因是缺乏必要的试验系统。针对这一问题,本文创造性地提出了一种考虑流-固-土多场耦合的多跨管道涡激振动试验系统。可实现对悬跨数量和悬跨段长度的灵活控制,具有较高操作性。在此基础上,利用该试验装置开展不同工况下多跨管道试验,研究不同流速下横流向和顺流向的涡激振动响应情况,并对试验结果进行了处理与分析。
1 试验装置
在考虑管土耦合的基础上,设计了跨肩和跨中土箱,通过土箱将管道分为多个管段,以此模拟海底管道多个悬跨段。整套试验装置由六个部分组成:拖曳水池、管道模型、跨肩处管土作用系统、支撑系统、轴向力施加系统和数据采集系统。
1.1 拖拽水池系统
如图1所示的拖曳水池隶属于天津大学水利工程仿真与安全国家重点实验室,长135 m、宽7 m、深3 m。试验中拖车速度范围为0.05~0.55 m/s,速度间隔为0.05 m/s。多跨管道涡激振动模型试验的雷诺数(Re)最大可达8 800,整体能够模拟实际海底流场条件。

图1 试验拖曳水池Fig.1 Towing tank in the experimental tests
1.2 管道模型
为了更好地观测管道在流固耦合作用下的涡激振动响应,需选取具有一定柔性的管道模型,具体模型参数如表1所示。

表1 管道模型参数(跨长比L1/L2=1∶2)Tab.1 Pipeline model parameters(L1/L2=1∶2)
整个管道模型分为内、外两层,由多种不同材料组合而成。模型的内芯为铜管,外部套有硅胶管、应变片等装置。现有研究表明,自由表面的存在会影响管道的旋涡脱落。当结构距离自由表面较近时,自由表面效应会对涡激振动产生显著影响。为了消除自由表面影响,管道模型与水面之间需要保持一定距离。参考相关试验以及计算流体力学(computational fluid dynamics,CFD)数值模拟结果,整套管道模型置于水面下大于20倍管径位置[16],即水面下0.5 m处。沿内芯薄壁铜管的轴向,依次布置G1~G7等7个均匀分布的测点位置,如图2所示。
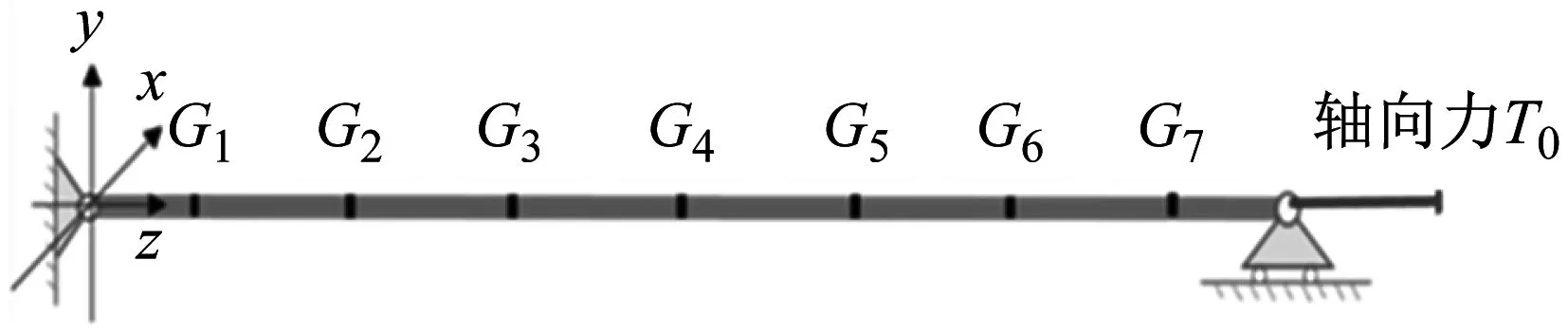
图2 各测点布置图Fig.2 Layout of each measuring point
每个测点处粘贴两组应变片,分别测量管道横流向和顺流向的弯曲应变,并将测量导线沿薄壁铜管轴向引出。内部薄壁铜管保证模型整体具有较大刚度,在能承受较高流速的同时也能激发高阶模态涡激振动。硅胶管不仅可起到扩大管径的作用,也能够保证与水接触的管道表面相对光滑平整,并对内部测量应变片起到防水绝缘作用,详细管道剖面如图3所示。

图3 管道模型剖面图Fig.3 Profile of pipeline model
1.3 跨肩和跨中土箱
实际的海底多跨管道的两端跨肩,以及相邻两跨间的跨中支撑多为海底土体,试验系统需可同时试验模拟管道跨肩和跨中处的管土作用。针对这一问题,创新性地设计了一套土箱装置,通过对土箱位置的改变实现不同的悬跨工况。
土箱内土样可根据实际海域的土体参数情况配制。为了更加接近实际海底悬跨管道工作环境,后续开展的试验土样以渤海海域为主要参照,土质为砂土,并对渤海海域实际采集的土样参数进行了大量前期测定,具体参数如表2所示。

表2 土体参数Tab.2 Parameter of soil
试验系统中悬跨管道的长径比L/D(L为管道悬跨长度,D为管道直径)最大可达到200,可满足不同管道跨长的试验条件。对于不同悬跨段数量的试验,可通过调整管道模型中部跨肩处土箱数量来实现。整套管土作用模拟装置可灵活组合,满足各种土体情况、不同跨段设置的试验需求。
为了减小土箱装置对流体作用的影响,土箱外型设计成流线型,以保证外部来流平稳。按照拖曳水池的整体结构和安装流程,设计两种土箱:端部流线型土箱和跨中流线型土箱。
1.3.1 端部流线型土箱
端部流线型土箱布置如图4所示。土箱包括一个土体舱和两个浮舱。深0.40 m的土体舱位于土箱中部,用于放置土样模拟土体边界,长、宽方向最大尺度均为0.50 m。试验过程中土样深度取决于管道模型位置及管道端部的埋深。土体舱的大小满足管道模型前、后的土体宽度和下方的土体深度均大于10倍管径。浮舱位于土体舱两侧,为试验装置的安装提供浮力。连接架采用高强度方形钢管焊接而成,布置于土箱外板与土体舱之间,为土箱提供支撑,同时可防止连接架对水流产生扰动。试验中采用的多跨模型是一根整体的管道模型。在跨肩部位,管道穿过土箱圆孔与土体接触形成土体边界。土箱内部管道埋置于土体中,形成管土耦合段,与外部的悬跨段共同构成多跨模型。

图4 跨肩土箱示意图Fig.4 Diagram of the soil box across the shoulder
1.3.2 跨中流线型土箱
跨中流线型土箱的内部构造与端部流线型土箱类似,主要区别是跨中流线型土箱的左、右两侧均为流线型,其单侧结构如图5所示。

图5 跨中土箱示意图Fig.5 Diagram of the soil box across the midspan
利用端部土箱模拟管道跨肩作用,在不安装跨中土箱的情况下,该试验系统可用于开展不同工况下的单跨管道涡激振动试验。在加入跨中土箱后,该试验系统即可成为多跨管道的涡激振动试验装置。可通过改变跨中土箱位置,改变土箱两边管段长度,从而达到不同的跨长比条件,改变跨中土箱数量可实现不同悬跨段数量的振动试验。将管道埋置于土箱之中,通过改变埋置深度可实现对不同管道埋置深度、埋置方式的试验模拟。
1.4 整体支撑框架
整套试验装置选取高强度钢管构建横向试验支持架,如图6所示。支持架顶部设有槽钢,通过螺栓连接槽钢,使整个试验装置固定于拖车底部。

图6 支撑装置Fig.6 Diagram of the support device
海底管道模型一端通过万向节固定于端部支撑板,另一端连接钢丝绳穿过支撑板。支撑板和土箱连接架的竖向高度根据拖车距水面距离和管道模型直径确定,管道模型与土箱和支撑板交汇需在同一水平面。
1.5 轴向力施加系统
轴向力施加系统包括钢丝绳、弹簧、张紧器和拉力传感器,通过调整张紧器获得试验所需轴向力,同时拉力传感器与应变采集仪相连,实时记录管道模型轴向力变化。轴向力施加系统可防止海底管道模型在试验过程中出现较大变形导致应变片损坏。为确保轴向力仅对管道轴向产生作用,轴向力施加系统的钢丝绳轴线与管道模型轴线须在与来流方向垂直的同一平面内。
1.6 数据采集系统
数据采集系统包括:电阻应变片、应变采集仪、计算机、摄像头、拉力传感器等。
试验中采用体积小、重量轻的电阻应变片测量管道模型的动力响应。由于多跨海底管道涡激振动不会激发高于4阶的响应模态,所以在沿管道轴向上布置7个测点分别粘贴两组180°对称的应变片。应变片通过测量导线连接采集仪,采样频率为100 Hz。管道模型的端部轴向力通过拉力传感器测量。将摄像头安装在拖车底部,通过摄像头记录管道的振动状态。
整体而言,可通过设置移动土箱装置,更改悬跨数量以及跨长,使得该试验系统能够灵活合理地进行多跨管道涡激振动试验。
2 试验设计
整套系统可实现跨长比、来流速度、管土作用和预张力等因素对多跨管道涡激振动影响的测试和试验研究。在管道模型顺流向和横流向上分别给定一个初始位移,让其自由振动,测定管道模型这两个方向上的自振频率和结构阻尼。选取典型工况条件进行了两跨管道涡激振动试验。相应工况如下:
(1) 跨长比
跨长比是不同悬跨段长度的比值。选取跨长比1∶2的工况进行试验分析,此时G1~G2测点位于短跨段,G4~G7测点位于长跨段,G3测点位于跨中土箱内。该工况设计能较好地满足试验要求,探索多跨管道的多模态响应以及模态竞争机制。
(2) 来流速度
通过调整拖车速度,改变水池来流速度v。在管道结构固有频率fn和直径D不变的条件下,通过改变来流速度可以实现约化速度的改变。选取来流速度范围为0.05~0.55 m/s,速度间隔为0.05 m/s。
(3) 管土作用
改变端部和跨间的管土接触宽度和管道嵌入深度,测量管道模型顺流向和横流向的应变。选取埋深为5D,对完全埋置的情况进行试验分析。通过观测涡激振动响应,可深入研究多跨管道的多模态响应以及模态竞争机制,观测相邻管跨之间能量传递现象。
(4) 轴向力
轴向力会对管道固有特性产生显著影响。试验前,分别采用理论分析和ANSYS有限元方法,对结构的固有频率进行计算,并预估结构振动状态,在张力为150 N时,结构在选定流速下能够达到锁频状态,并且可激发二阶模态,符合试验需求。因此,在管道模型端部施加150 N轴向力。
试验通过观测多跨管道涡激振动响应、相邻管跨之间的相互作用形式等,从而揭示多跨悬空管道的流-固-土多场耦合动力学特性,探索多跨管道多模态响应以及模态竞争机制。
3 结果分析
试验过程中,在较低流速下,管道悬跨部分振动并不明显。当流速达到0.2 m/s后,振动幅度显著增加。该现象一定程度表明结构已经达到锁频状态,涡激振动特征明显,后续分析重点关注锁频状态下结构响应。
试验中应变数据采样频率是100 Hz。试验中拖车运动产生的干扰信号频率不到1.0 Hz,远低于悬跨管道涡激振动的响应频率。管道涡激振动的最高响应频率(包括倍频)不超过40.0 Hz。在试验数据进一步处理之前,先采用带通滤波的方法消除低于1.0 Hz的低频拖车运动干扰信号和高于40.0 Hz的高频噪音信号。
图7给出了来流速度分别为0.1 m/s、0.3 m/s和0.5 m/s时各测点处横流向应变时程曲线图。随着来流速度的增大,各跨段的应变幅值都有明显增大。在较低流速时,长跨段和短跨段的应变幅值大小较为接近,并无明显区别,且整体响应情况不剧烈,应变值也较小。随着流速的增大,长跨段应变值对流速变化更为敏感,增长幅度更明显。当流速较大时,各测点的应变时程曲线较为稳定,具有明显的简谐振动特性。响应较为明显时,G4测点与长跨段其他测点的应变值有所差别,可能原因是G4测点距离跨中土箱较近,受到邻跨段影响以及跨中土体影响,导致应变响应有所变化。

(a) v=0.1 m/s

(b) v=0.3 m/s
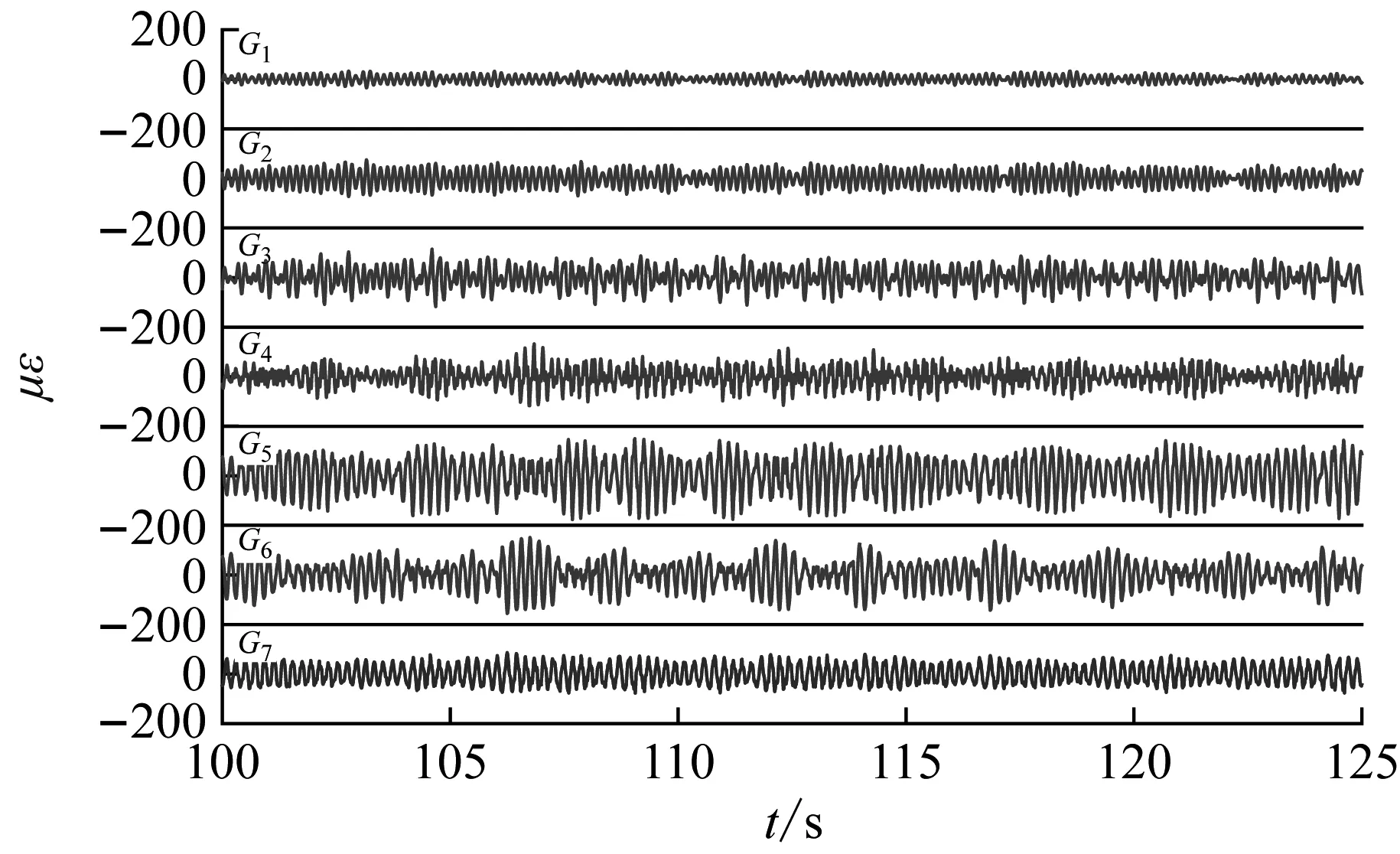
(c) v=0.5 m/s图7 不同流速下横流向应变时程图Fig.7 Cross-flow strain history diagram at different flow velocity
图8给出了流速为0.3 m/s时各测点处横流向和顺流向应变时程曲线。对于短跨段,横流向和顺流向的应变响应幅值较小,接近零。而长跨段则出现了明显的周期性变化应变幅值,与短跨段响应情况有较大差异。可能原因是短跨段的长度较小,其固有频率相比长跨段更高,两个跨段在相同流速下的振动状态不同,导致响应程度相差较大。管土作用处的测点G3附近应变幅值受土体影响,与其前、后G2和G4测点处的应变幅值有较大区别。受到跨中土体影响,G4测点与长跨段其他测点的应变值有所差别,而且横流向应变受土体作用影响比顺流向更明显。同时横流向最大应变幅值更大,约为顺流向的2倍,说明此时横流向振动比顺流向更为剧烈,响应更加剧烈。应变幅值变化规律说明土体作用会对管道振动特征产生显著影响,并且多跨管道不同跨段响应情况会有区别,管跨相互之间存在着影响。

(a) 横流向

(b) 顺流向图8 各测点应变时程图Fig.8 Strain history diagram of each measuring point
图9给出了流速为0.3 m/s时各测点处横流向和顺流向应变响应的频谱图。

(a) 横流向

(b) 顺流向图9 各测点应变频谱图Fig.9 Strain spectrum diagram of each measuring point
由图9可知,不同悬跨段的频率成分和谱峰频率具有一定差异,长跨段管道横流向的主控频率为3.56 Hz,G1、G2、G3测点处出现了一些7.56 Hz频率成分,且短跨段处的明显小于长跨段。顺流向和横流向的频率成分和谱峰频率较为接近,主控频率均在3.56 Hz附近。此时,顺流向振动与横流向振动相互耦合,对管道的整体动力学特性影响不可忽略。
4 结 论
本文创造性地设计了跨肩和跨中流线型土箱,构建了一套考虑流-固-土多场耦合的多跨管道涡激振动试验装置,可用来分析多跨管道跨间作用对管道涡激振动的影响。同时,利用该试验装置开展了一定埋深下的两跨管道涡激振动试验,研究了管道横流向和顺流向应变响应特性。结果表明:
(1) 设计试验装置能够合理地模拟悬跨管道边界的土体作用。该装置可用来开展不同流速、轴向力、跨长比和土体条件下的多跨管道涡激振动试验,其结果可为多跨管道涡激振动的跨间影响等研究提供新的试验设计示例,为海底多跨管道试验提供新思路。试验结果可为后续理论研究和数值模拟提供数据参考。
(2) 考虑多跨管道的跨间作用时,不同跨段的应变幅值及响应频率在不同流速下有较大差异,其中长跨段更容易激发涡激振动。横流向最大应变幅值约为顺流向的2倍。靠近跨中土体段部分,由于受到相邻跨段的影响,结构振动剧烈程度有所增加;在远离跨中的位置,跨间相互影响程度较小,结构振动情况未发生明显变化。
(3) 靠近跨中土体段的结构位移受到土体约束影响,不同跨段间的相互影响会通过跨中管土耦合段进行传递,跨中段管土作用会影响多跨管道的振动特征。
