基于灰色预测容错时钟同步算法

陆 禹，张 力，张凤登

(上海理工大学 光电信息与计算机工程学院，上海 200093)

随着计算机信息化高速发展，各种网络化系统大都可以对数据进行自我采集和处理。分布式系统作为典型的网络化系统，其研究也受到越来越广泛的关注[1]。随着分布式系统复杂度和规模的增大[2]，为系统分配的节点数目也不断增多，系统发生故障的概率也越来越高。面对目前有严格要求的实时系统，确保高精度的时钟同步是避免故障且维持系统有效控制和精确运行的必要条件之一[3]。在满足时钟同步的前提下，系统还需要具有一定的容错性[4-6]，使得分布式系统在其中几个节点出现断线时，仍然可以保持正常节点的时钟同步。

目前，国内外研究人员已经提出了许多基于节点双向交换各自时钟信息的时钟参数估计算法来解决时钟同步中的精度问题，并取得了一定成果[7-11]。文献[12]通过将卡尔曼滤波算法和自然选择粒子群算法结合，提高了无线传感器网络的时钟同步精度。

本文主要致力于研究经典分布式系统内部时钟同步算法在运行过程中遇到的通信链路丢失故障的解决方案，并基于此提出一种可以容忍该故障的灰色预测容错时钟同步算法。

1 系统模型描述

本文采用广播式通信网络LL(Lundelius Lynch)模型[13]，并将时钟状态修正和时钟速率修正相结合。该模型在每轮次中重复执行时钟同步算法，其节点仅在特定时刻发送与时间相关的消息，有效降低了获取时间节点消息的通信成本。

从有关Cristian和LL模型的研究中可知，基于远程时钟读取技术时钟的最大估算误差为2d(1+2ρ)-2(δ-ε)，而基于初始同步的时钟检测技术时钟的最大估算误差为2(ε+β+ρδ)[14]。其中，d表示以A节点时钟为基础所测量的A节点发送与B节点回复过程的总路程的一半，ρ为时钟漂移率，δ为可能存在的通信延迟的中值，ε为通信延迟的一个细微不确定度，β为一个先验的固定值，表示初始时刻节点间的同步程度。由于LL模型不需要请求-回复机制，所以它的通信开销更小。对于远程时钟读取模型而言，由于节点之间不是点对点地发送消息，所以一定程度上增大了读取时钟的误差，但是在广播式网络中可避免此类问题。

该模型对重同步周期TP及节点的初始状态有一定要求，下面对模型进行条件假设。

1.1 条件假设

采用模型分析算法时，需对模型进行一定条件的假设，这样才可以合理地分析算法的性能。本文将分布式系统中所有节点用集合P表示，每一个节点进程pi∈P都对应一个用Hpi表示的本地时钟。具体假设如下文所述：

假设1假设本地时钟漂移率处在一个合理范围内，即一个极小的常数ρ>0。本文定义在任意真实时间t时，本地时钟Hpi(t)与ρ都存在如下关系

(1)

式中，Hpi(t)表示i节点在真实时间t时对应的本地时钟值；ρ表示i节点的本地时钟漂移率；

假设2系统内节点间消息通信延迟有界，也就是节点之间通过任何链接发送、传输、接收任何消息所产生的通信延迟Td在范围[δ-ε，δ+ε]内。即

Td∈[δ-ε，δ+ε]

(2)

当该假设成立时，时钟同步算法保证了系统中各个节点之间的最大逻辑时间偏差值在一定范围内，也就是精密度γ；

假设3分布式系统中故障节点有限，设定系统中故障节点数不能超出系统总节点数的三分之一

n≥3f+1

(3)

式中，n表示系统中所有节点的总数目；f表示系统中拜占庭故障节点的数目；

假设4为了更加容易地分析流程，可以忽略消息处理产生的延迟；

假设5节点在系统开始工作的初始时间点为T0，A节点在初始时间点的真实时间为CA(T0)，B节点在初始时间点的真实时间为CB(T0)。系统的正常工作节点在初始时间点时同步在一个固定先验范围内，表达式为

|CA(T0)-CB(T0)|≤β

(4)

式中，β为一个先验的固定值；A和B为系统中可正常工作的节点。

假设6时钟同步时，A节点在发送自身节点时钟消息时，其余正常工作节点和A节点处在同一轮次中。因为系统需要进行重复的时钟同步，因此要对重同步周期TP做出以下的假设

TP>2(1+ρ)(β+ε)+(1+ρ)max{δ，β+ε}+ρδ

(5)

且

TP≤β/4ρ-ε/ρ-ρ(β+δ+ε)-2β-δ-2ε

(6)

若没有特殊指明，本文的其它假设与前提条件都与LL模型一致。

1.2 模型具体应用

单个节点通过广播的方式将自己的时钟信息发送给其它各个节点[15]。系统的时钟同步是一个重复的周期性过程，可以将逻辑时钟用轮次的形式表示时钟同步过程。每一轮次中，时间的总长度L是恒定不变的，一轮次中有k个宏时隙，则表达式如式(7)所示。

L=k×ng

(7)

式中，ng表示系统全局时间的一个宏时隙长度。由于时钟同步是周期性过程，因此其长度同样要满足上述重同步周期的条件。每轮要留出固定长度的时间作为修正段，例如FlexRay网络中通常称为NIT(Network Idle Time)段[16]，节点的时钟逻辑时间在NIT段内进行时钟状态修正和时钟速率修正。本文用4个节点在完全同步的状态下作为示范说明第i轮的结构，节点的相关参数如表1所示。

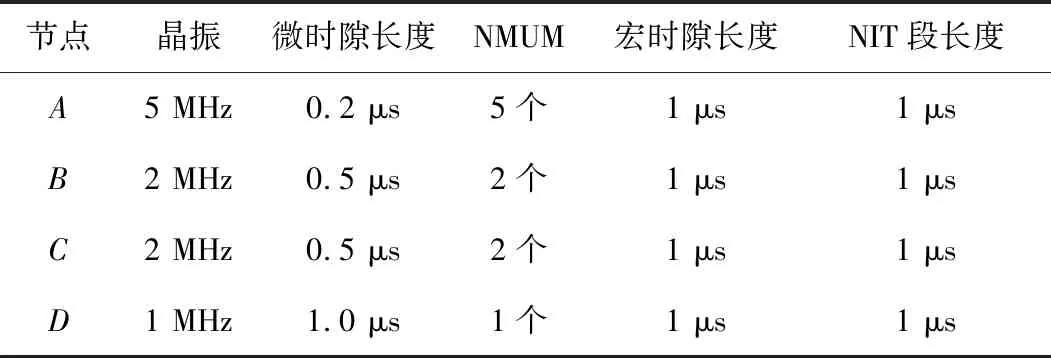
表1 节点参数表

图1 理想状态下第i轮状态图Figure 1. State diagram of the i round in an ideal state

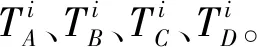
2 Grey-FAT算法

2.1 灰色预测

GM(1，1)(Grey Model)是使用一阶微分方程对一个变量建立灰色预测的方法，其原理是对某一数据序列用累加的方式，生成一组趋势明显的新数据序列，并按照新的数据序列的增长趋势建立模型进行预测，然后再用累减的方法进行逆向计算，恢复原始数据序列，进而得到预测结果。

GM(1，1)预测过程具体如下：

当A节点发生通信链路丢失故障时，设有一组前n轮未发生通信链路故障时通过FTA(Fault Tolerant Average)算法得到的时间偏差序列，具体如式(8)所示。

X(0)=[x(0)(1)，x(0)(2)，…，x(0)(n)]

(8)

由原始的时间序列数据生成一阶累加生成序列为X(1)

X(1)=[x(1)(1)，x(1)(2)，…，x(1)(n)]

(9)

式中

(10)

同时生成一阶累加生成序列的紧邻均值生成序列Z(1)

Z(1)=[z(1)(2)，z(1)(2)，…，z(1)(n)]

(11)

式中

(12)

建立灰微分方程

x(0)(k)+az(1)(k)=b，k=2，3，…，n

(13)

式中，a、b分别为发展系数和灰作用量。其白化方程为

(14)

则GM(1，1)模型的解为

(15)

式中，a和b由最小二乘法计算得出，求解过程为

A=(a，b)T=(BTB)-1BTY

(16)

式中

(17)

最终GM(1，1)模型对原始偏差值序列的模拟值为

(18)

当发生链路故障时，当前轮次A节点的时钟偏差值如式(19)所示。

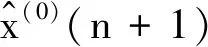
(19)

2.2 精度校验

使用GM(1，1)模型对时钟在出现通信链路丢失故障和通信链路性能故障时的修正值进行预测。

判断已知修正值序列数据是否符合灰色预测模型，需要进行预测模型的精度校验。模型精度的校验通过方差比C和小概率误差P来评估，计算流程如下所示。

首先，需要计算残差ε(k)

(20)

再计算相对误差Δ(k)

(21)

然后计算原始序列的标准差S1和残差序列的标准差S2

(22)

(23)

则方差比C为

(24)

小概率误差P为

(25)

模型拟合的精确度由C和P共同决定，GM(1，1)精度检验等级参照表2。

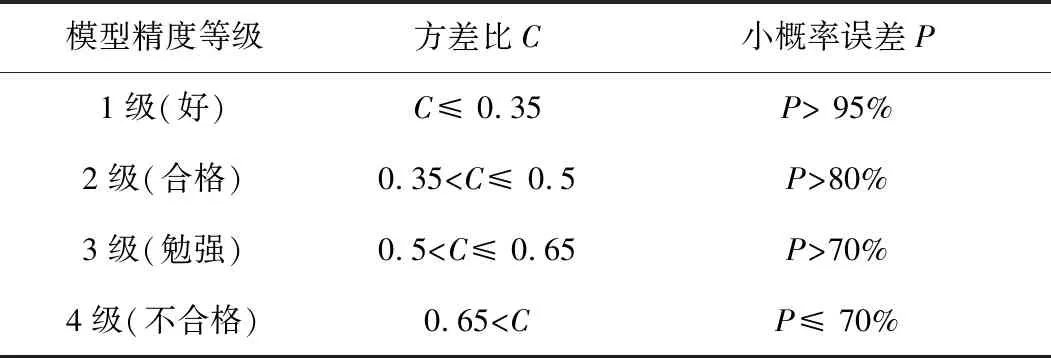
表2 GM(1，1)精度检验等级

2.3 算法流程

该算法在LL模型基础上，通过一定的假设条件，利用初始时钟同步的时钟检测技术，来收集到其余节点的时钟值。此外，该方法还在传统的FTA算法基础上加入了灰色预测，以此来解决通信链丢失故障。Grey-FTA算法的流程图如图2所示。

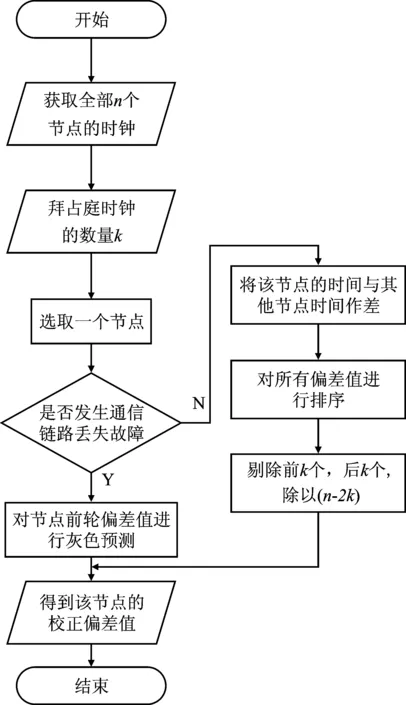
图2 Grey- FTA算法流程图Figure 2. Flow chart of Grey- FTA algorithm

3 实验与结果分析

3.1 实验参数设置

本文采用了LL通信网络模型，故需将模型中各项条件参数假设为相应常数值。具体的条件参数有时钟漂移率ρ、远程时钟读取最大误差ζ、节点通信最大延迟β、同步初始状态偏差δinit以及时钟重同步周期TP。参考汽车或航空器中参数相应常见真实数值范围，本文的设定如表3所示。

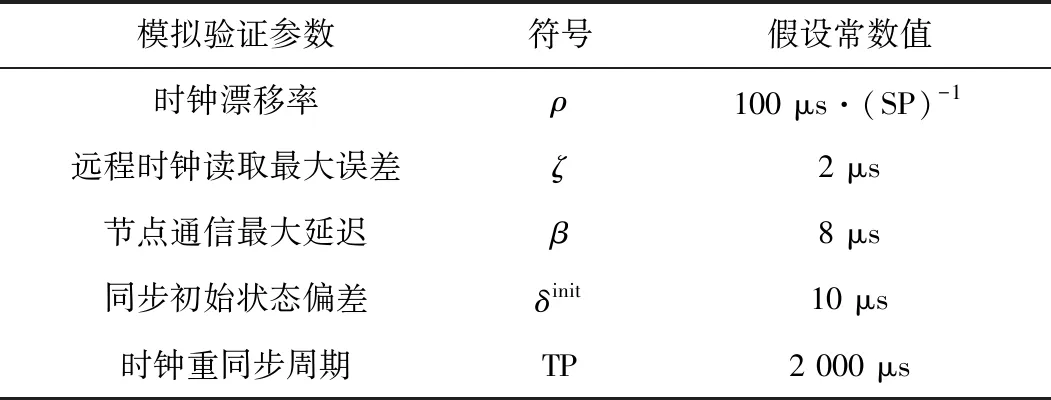
表3 实验参数假设常数值

为了体现Grey-FTA算法对于通信链路故障的容错能力，模拟验证实验将本文所提算法与原始处理(Native)、水平滑动估计(Moving-Horizon Estimation， MHE)[17]和全局滤波估计(Overall Filtering Estimation， OFE)[18]这3种处理通信链路故障方法进行对比。实验节点参数设置如表4所示。

表4 实验节点参数设置

3.2 实验步骤

实验中首先构建共含5个模拟验证节点的CAN总线网络，分别为Node1～Node5。真实情况中总线型网络的通信链路故障表现为：在通信周期内，节点无法正常访问通信媒介，即发送或接收总线报文失败[19]。在实验中为了模拟通信链路故障，专门设置一条特殊的Blank报文，当某个节点发送该报文时，即相当于该报文正常发送失败或接收节点接收异常。对于所有节点都以一定的故障概率发生通信链路故障，在模拟验证中以CLFP(Comm -Link Failures Probability)表示，即在一个通信周期内发生一次报文通信因链路故障而失效的概率。具体步骤如下：

步骤1按照起始时刻、同步初始状态偏差开始时钟同步，所有节点内部运行相应容错时钟同步算法；

步骤2随机生成所有模拟验证节点的这一轮时钟同步周期内的偏移值，并且均保存并存储在节点的通信列表文件中；

步骤3按照通信链路故障概率，随机决定这一轮是否发生通信链路故障，即发送Blank报文；

步骤4在每个节点感知到通信链路故障后，分别按照Native、Grey-FTA、MHE-FTA、OFE-FTA4种处理方式或算法得到该轮的时钟修正值，并计算出修正后实际逻辑时钟时间偏差，从而完成一个时钟同步周期；

步骤5更新每个节点保存所需的最近若干轮同步偏差数据，存储深度最大为2 048；

步骤6随后循环重复步骤2～步骤4。

3.3 结果对比分析

所有同步算法仿真实验的记录数据均保存在节点通信列表文件中，在仿真结束后可由log文件导出得到。由于数据规模较大，所以这里截取所有算法前50轮时钟同步过程中收集记录的实验结果数据，如表5所示。

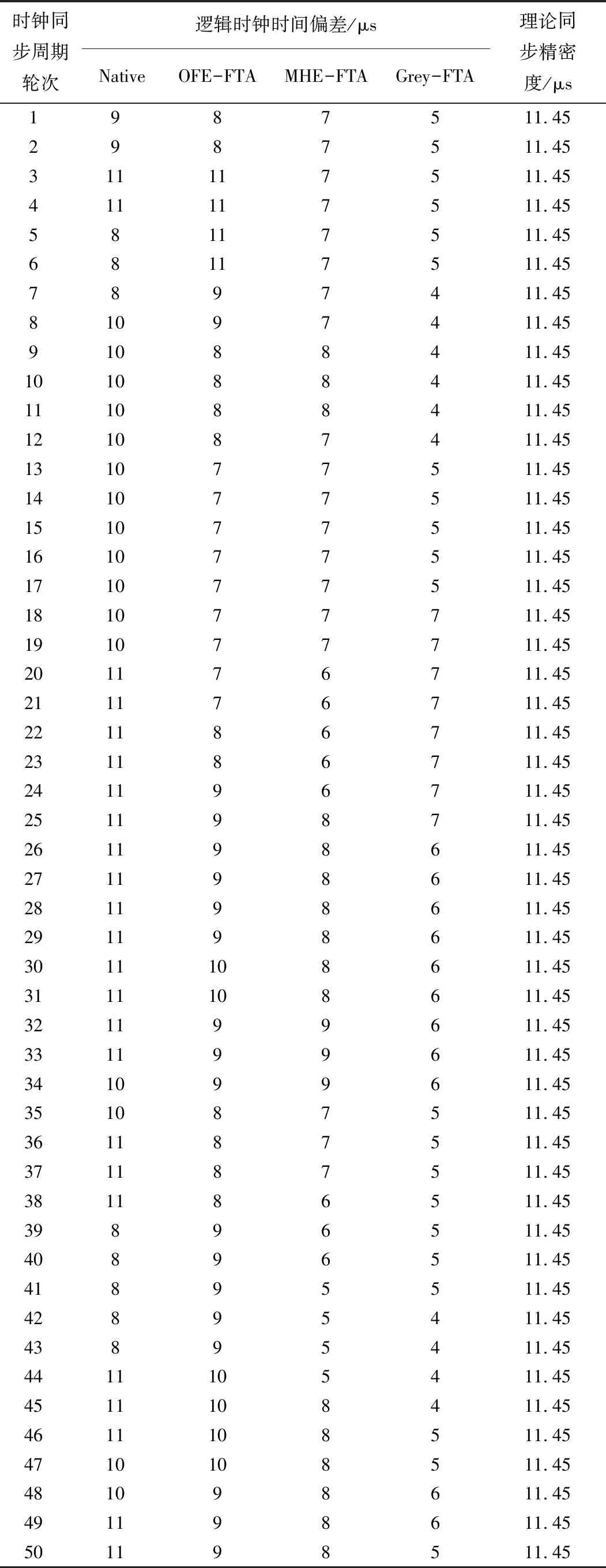
表5 基于LL模型的容错时钟同步算法实验结果数据

采用Grey-FTA容错时钟同步算法的同步过程与其他算法的对比如图3所示，横坐标为进行时钟同步轮次，纵坐标表示逻辑时钟偏差。

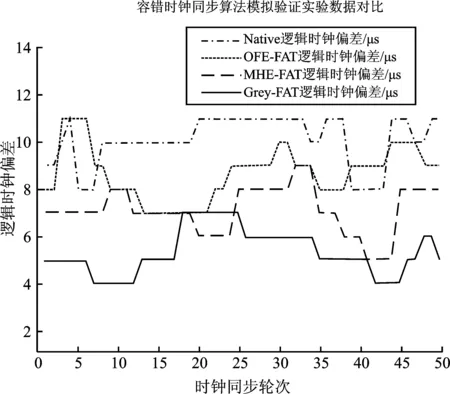
图3 容错时钟同步算法模拟验证实验数据对比Figure 3. Comparison of simulation and verification experiment data of fault-tolerant clock synchronization algorithm

从图中可以发现，与MHE-FTA以及OFE-FTA容错时钟同步算法修正过程相比，Grey-FTA算法的修正过程更加主动积极，其修正效果也更加显著。此外，通过对比整体的时钟同步轮次来看，Grey-FTA算法同步后逻辑时钟时间偏差量最小，同步状态最稳定，这从结果上证明了该算法的正确性、有效性。更重要的是本文所得算法的系统时钟同步精密度同比提高了24.3%，证明了Grey-FTA算法的优越性。

4 结束语

本文提出了一种适用于时间触发实时系统的预测自适应Grey-FTA算法，该算法不仅实现了对于时钟两面性故障的容错，还解决了时钟节点出现通信链路丢失故障不能进行时钟偏差的校正的问题。同时，该算法不局限于某一个具体的网络通信系统，对于网络的具体结构没有进行约束，理论上可用于符合本算法基本模型要求的大多数时间触发式系统或网络的内部时钟同步。但是，本文的灰色预测方法存在精度等级的限制，对于大量离散不合理的数据所预测的值参考意义有限，后续的研究可以将此算法用于更加完善的预测模型中。