矿用重载电力机车车体结构刚度变化控制系统

申利燕，苗建明

（1.山西工程职业学院，山西 太原 030032；2.中山大学，广东 广州 519082）

1 引言

对于矿用重载电力机车而言，其车体结构的静刚度和动刚度是两项最为重要的指标[1]，如果不对刚度进行合理的控制，其自身变化就会直接影响机车的各项性能。刚度是一种会随着响应频率变化而变化的能力，其响应频率变化的幅度数值和刚度是成正比的[2]，当车身的刚度不足时，响应频率就会随之降低从而产生共振，影响NVH（即共振Noise、噪声Vibration 和不平顺性Harsh⁃ness）以及整体的可操纵性、安全性、稳定性、碰撞性、耐久性和经济性等能力。因此，对刚度变化进行实时控制，可有效提高机车安全性能，并保障各项指标的正常实现。在相关学者研究中，文献[3]提出了高速列车车体结构刚度优化方法，以有限元理论、非线性理论和结构准静态理论为基础，构建刚度仿真模型，利用结构热力耦合分析车体刚度，完成车体补强设计。但在车体刚度变化的掌握方面需要完善。文献[4]考虑摩擦力、转子偏心和电枢轴的非线性刚度，建立动态微分方程研究机车牵引系统的分岔和混沌行为。仿真结果揭示了间歇分岔的复杂动态，虽然为摩擦故障诊断提供参考依据，但对机车刚度的变化。文献[5]研究了端齿连接结构接触刚度的解析模型，该方法考虑了接触界面微观形貌的问题，将GW粗糙表面模型带入刚度分析的公式中，得到了表面微观形貌对端齿接触刚度的影响结果。该方法求解结果与有限元结果相近，但在刚度变化的捕捉有待进一步完善。

综上所述，设计一种重载电力机车车体结构刚度变化控制系统。通过详细的系统控制流程，对车体结构刚度进行计算，根据计算的刚度数值给出相应的控制算法，提升刚度。尽可能地减少在受力情况下车体的变形程度，并降低机车在振动时产生的振幅，增强抗振性，提高安全性能。性能测试结果证明，所提系统的控制算法简便且易于实现，能够对车体刚度实现有效控制，具有很好的减振效果，能够保证矿用重载电力机车的车体结构安全运行。

2 重载电力机车车体结构刚度变化控制系统

2.1 控制系统整体架构

给出重载电力机车车体结构刚度变化控制系统的整体架构，如图1所示。

图1 刚度控制系统整体架构Fig.1 Stiffness Control System Architecture

2.2 系统硬件设计

重载电力机车车体结构刚度控制系统的硬件部分主要由四个部分组成，分别为：传感器、刚度调试器、刚度变化控制器及控制执行机构。

（1）系统所使用的传感器[6]是由目前最为实用的一台891型拾振动器及两台CY3−8A型传感器共同组成，一台振动器用于监测系统机器内部结构的速度绝对值，而另外两台传感器则用于测量液压缸内外的压力差[7]。

（2）安装刚度调试器是由一个安装控制器、一个电磁阀门[8]和4条软油管共同组成。其主要是在系统进行安装及后期调试检修时使用，只需要一台调试器就可为多个控制系统同时使用，能够保证调试精准度和质量安全。

（3）刚度变化频率捕捉器是根据信号传输为依据，通过一个尺寸为（200×150×100）的硬件匣子作为传输媒介，其主要由刚度信号接收器、电路判断机制、功率驱动机制等多个部分共同组。其通过接收器取得的对应信号，再经过电路判断及功率驱动处理后，作为最后的控制信号输出给刚度液压控制模块，让其实现刚度变化控制。

（4）刚度变化控制系统中最为重要的一个执行步骤就是液压控制执行机构。其通过系统内部的上下部分相对重复工作，根据计算的刚度数值利用机构内的关键推杆工作积攒变形能并释放，经过一系列的循环最终完成刚度变化的控制，达到减振效果。转向架是保证轨道车辆安全运行的主要部件之一，列车的运行稳定性和乘坐舒适性与转向架的悬挂特性密切相关，主要的刚度变化也主要集中在此结构中。刚度控制系统硬件组成结构，如图2所示。

图2 刚度控制系统硬件组成Fig.2 Hardware Composition of Stiffness Control System

2.3 系统软件设计

2.3.1 车体刚度计算

大多数情况下，都会用数值来表达控制系统的刚度状态。比如，弯曲刚度和扭转刚度就是用来表示抗弯曲能力及扭转变形能力的[9]。因此，可把重载机车的车身结构看成一个呈线性的大型系统，根据线性特质与力学特性的一致性，将矩阵刚度模型与模态进行关联，通过此矩阵模型来反映力学的特点从而计算刚度数值。

若将矩形框架看成刚度变化控制的一个线性系统，就可以将系统受到外力时产生的向量表达为以下关系式：

式中：VB—线性系统受到外力时产生的向量系数。

一般情况下，施加载荷的施力点与其载荷方向一般保持一致（即与刚度矩形框架的水平方向呈垂直状态），则载荷量与载荷施加点位置偏移的比值就可表示为：

式中：z1～z6—点1到点6与水平方向保持垂直的位移量；KB—刚度变化参数。

基于刚度矩形框架的扭转刚度结构，如图3所示。

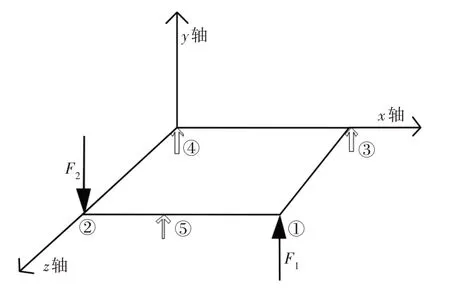
图3 基于矩形框架的扭转刚度Fig.3 Torsional Stiffness Based on Rectangular Frame

在矩形下摆位置的1、2处施加同等大小的力F，让力F之间方向保持相反，并与矩形平面呈垂直状态，且对3、4、5位置处对应的自由度x、y、z实现约束。

如果将其记作为F1=F，F2=−F，那么就可以根据静态平衡原理［10］，得出关系F3=−F，F4=F，将其表达在扭转刚度矩形线性系统中，就可以得出以下向量关系式：

式中：VT—在扭转刚度情况下产生的向量系数。

此时根据上述得出的扭转刚度向量系数，基于矩形框架的扭转刚度就可用施加在线段L12中点的扭转距离与L12及L34间的扭转角度来表示，关系式为：

式中：L12—扭转刚度矩形的前长；L34—扭转刚度矩形的后长。

基于n自由度线性的刚度变化控制系统，基本的常规自由振动表现为：

式中：M—关于变化控制系统的矩阵；K—刚度变化系统矩阵；x—位移运动的列向量。

对较为复杂的线性刚度变化控制系统来说，式（5）是属于互为耦合数的微分方程，对此方程进行求解需满足x=Φη，得出解耦后的函数为：

式中：Φ—控制系统矩阵的模态形式；η—模态的位置坐标。

因为此系数在各阶级的模态向量值都与质量及刚度矩阵相关，且两两相交，所以就可推断Mm=ΦtMΦ为对角矩阵，主要针对在各阶级矩形模态的质量；Km=ΦtKΦ也为对角矩阵，但与前者不同，其主要针对在各阶级矩形模态的刚度状况。第i阶级的矩形模态表达关系式为：

式中：ωi—在第i阶级对角模态的角频率；fi—自然情况下角频率的正常数值；km.i—矩形模态的质量。

根据动力学结构原理及重载电力机车自身的结构特征，可得出基于上述线性刚度变化控制系统的静态方程：

将x=Φη代入式（9）中，再乘以Φt，就可以得出关于线性控制系统在静态与动态下的相互关系：

当矩形模态框架在静止状态下受到压力而导致形变时，给出在第i阶级状态下的关系为：

再将式（12）代入到式（2）得出扭转刚度数值，得出刚度xj与各阶级下模态向量的关系：

以此类推，就可得出在各阶级下刚度及其扭转刚度的参数关系，就可得出最终的刚度数值xj。

2.3.2 车体刚度控制

重载电力机车刚度变化的控制主要依赖于计算得出的具体刚度值，通过数值再进行判断并利用系统控制机器给出相应的控制动作，其具体工作过程，如图4、图5所示。

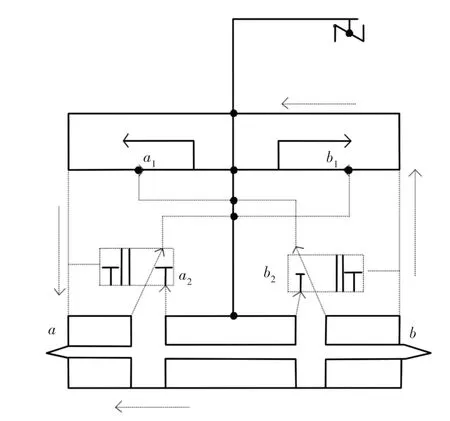
图4 刚度变化控制机制向左工作运动Fig.4 Stiffness Change Control Mechanism Working to the Left

图5 刚度变化控制机制向右工作运动Fig.5 Stiffness Change Control Mechanism Working to the Right

从图4中可以看出，此控制系统的内部结构分为上下两个部分，当图4中上部分向左进行控制运动时，推杆a就会发生一个推拉动作，液压工具阀门a1关闭，进而使两侧的软油管路互相断开，a处的内部压强逐渐提升，a处推杆就会随着压强的升高慢慢被拉伸，以便储蓄变形能量；当b处推杆受到压强时，液压工具阀门b1开启，两侧的软油管路会互相连接，b推杆处不会发生形变。

当控制器的上部分不再相对向左进行控制运动时，就会反向向右进行控制运动，这时，推杆a就会一直保持推拉的动作，而推杆b也会跟随推杆a同时受拉，液压工具阀门b1关闭，将两侧的软油管路互相断开，b处的内部压强逐渐提升，再控制软油管路的将液压工具阀门a1断开，使a1处两侧的软油管路互相连接，这时a推杆处及其所连接的器件中所有储存的变形势能都会被释放，再随着b内部油压的升高，油路控制机制就会将在三位工作的阀门b2推向二位处工作，而a1也会回到原本的位置并保持基本的常设状态；与此同时，b处推杆会逐渐呈拉伸状态，以便储蓄变形能量。

如图5过程所示，在向右控制运动工作结束时就会开始循环重复动作即继续反向运动向左工作。随着变形能力的不断积蓄，振动会不间断持续产生，可以反复重复上述动作。通过内部结构左右的不断改变，刚度变化控制系统会随之不断吸收变形能量再进行释放，进而达到对刚度变化的控制，实现减振效果。

3 仿真实验

为了验证系统对重载电力机车车体结构刚度变化的控制效果，将神24电力机车作为实验对象，该电力机车长106m，具有6节编组，最高运行时速为120km，车组功率为28800kW，将该机车的刚度数值作为初始数据，建立三种不同情况下的刚度控制测试，全面测试所设计系统的控制效果，并进行对比分析。刚度测试软件界面，如图6所示。

图6 刚度测试软件界面Fig.6 Rstiffness Test Software Interface

其中，三种刚度情况如下：

（1）初始无控制的情况，在重载电力机车内没有任何其他工作元件干扰工作，且没有安装刚度变化控制器件，此时的刚度数据为基本的初始数据，刚度数值为100。

（2）在机车车体内部增加横梁的情况，增加刚度控制难度，以原有车体结构为基础增强车体振动，从而增加刚度变化数值，刚度数值为200。

（3）利用本系统对上述两种情况进行控制。将控制参数设置为KB10−1m、KB10−2m、KB10−3m、KB10−4m、KB10−5m。

刚度变化控制结果，如表1所示。

表1 基于同种特性的刚度变化控制结果Tab.1 Stiffness Variation Control Results Based on Homogeneous Characteristics

其中，xj表示刚度初始数值，根据如表1所示的对比结果分析可得：

（1）重载电力机车在无外物干扰及内部没有控制元件的情况下，通过系统根据其原始刚度数据进行控制后，得出的百分比基本都保持在90%以上。由此可见，此系统的控制整体效果优异，且在控制参数不断下降的情况下也能保持一个合理的减少，效果相差不大。

（2）重载电力机车在无外物干扰，但内部增加负重横梁的情况下，通过系统对其进行刚度变化控制后，得出的百分比基本都保持在85%以上。对于在车体增加了近5t的负重后，达到刚度控制效果来看，系统的控制效果已经能够满足实际需求。因为在一般情况下，如果车体结构负重不断增加就会导致其表面逐渐产生压力从而发生形变，增强刚度数值，共振也就会同时上升进而威胁安全缩短车体寿命。

4 结论

通过构建的刚度变化控制系统分析可得出以下结论：

（1）控制系统的硬件构造简单不需要复杂的内部结构，器件耗用量较小、操作过程简单且便于实现刚度变化控制。

（2）基于矩形线性原理的计算方法直观简便，且准确性高。

（3）最终的刚度变化控制机制工作步骤简洁，具有较强的自控能力及程序恢复能力，在无法对其进行干预的情况下也能根据原本初设给出相应的控制方案，且效果优异，不仅能有效减少车体内部的共振现象，还能减少机车的耗用量。

（4）仿真结果证明，基于重载电力机车车体结构的刚度变化控制系统具有较好的控制效果。