车用电机定子电流新型优化控制方法
2023-03-19周雅夫王翰涛连静
周雅夫,王翰涛,连静
(大连理工大学运载工程与力学学部汽车工程学院,辽宁 大连 116024)
1 引言
内置式永磁同步电机(IPMSM)具有非线性,强耦合的特性,在电机实际运行过程中电机参数的变化导致电机难以实现在所有工况下对直轴电流和交轴电流完全解耦,无法实现交直轴电流最优匹配控制[1]。为了解决因耦合特性造成IPMSM控制性能无法达到最佳效果的关键问题,学者们开展了大量关于IPMSM解耦控制和电动车驱动系统设计的研究[2]。
常见的解耦控制方法主要有前馈补偿解耦[3],交叉内模解耦[4],模糊神经解耦[5],自适应动态解耦等。其中前馈解耦和交叉解耦都非常依赖精确的电机数学模型和参数辨识模型,参数的扰动导致解耦效果不理想;神经网络逆解耦法系统存在计算难度大且工程应用困难的问题;模糊神经网络解耦需要基于经验建立的规则,工程上实用的价值不高;自适应动态解耦要求系统具有较高的比例增益,极其容易造成系统超调,导致系统的不稳定性增加。因此,常规的解耦方法不能完全实现全工况范围内的线性解耦控制。
随着自适应控制和人工智能技术的发展,强化学习在控制领域得到了广泛的应用[6]。近年来,基于强化学习的控制方法在电机控制领域已经得到一定程度的应用。文献[7−8]提出了一种基于Actor−Critic 网络的永磁同步电机速度控制器设计方法,仿真和试验结果验证了这种方法具有良好的响应特性;文献[9]提出了一种基于混合Zeigler−Nichols强化学习的方法优化PID参数实现直流电机的速度控制,仿真验证了方法的可行性;文献[10]提出了一种基于深度梯度下降的强化学习算法的伺服电机速度控制方法,通过仿真分析验证了该方法能自适应电机的负载的扰动。综上,提出了一种基于深度确定性策略梯度的车用电机定子电流优化控制方法,在不对交直轴耦合项电压进行补偿解耦的情况下实现IPMSM 交直轴电流的最优匹配控制,克服了参数扰动带来的交直轴电流匹配不佳的影响。
2 内置式永磁同步电机耦合特性分析
稳态情况下,电机的d−q轴电压方程如式(1):
式中:ud和uq,id和iq,Ld和Lq—交直轴的电压,电流和电感;Rs—定子电阻;ψf—转子磁链;ωe—转子电角速度。
由式(1)可推导出稳态下的电流方程,如式(2):
其中,系数矩阵可以表示为:
对稳态条件下IPMSM的电流方程(2)分析可知,Id和Iq同时受ud和uq的影响,而ud和uq对Id和Iq的影响程度取决于系数kdq、kdd、kqq、kqd的大小。由方程(2)可知,系数是关于电机电感、电阻以及电角速度的函数,故而ud和uq对Id和Iq的影响随着电机参数变化会呈现动态的变化。对电流方程中的系数模型进行定量分析,电角速度在(0~500)rad/s区间变化时系数kdq、kdd、kqq、kqd的变化情况,如图1所示。

图1 稳态情况下电流方程系数随速度的变化情况Fig.1 The Current Equation Coefficient Variation with Speed Changing Under Steady State
结合式(2)和图1可以得出耦合项电压的系数与相应的交直轴电压的系数比值的绝对值随着电角速度逐渐增加,图1 中的(a)和(b)分别反应了直轴和交轴电流方程中ud和uq系数大小随电角速度的变化情况,系数kdq、kdd、kqq、kqd随电角速度增加呈非线性变化,且由低速阶段到高速阶段绝对值发生显著变化。
由电压方程可知,电感是影响解耦效果的主要,电感易受电机定子电流的影响。一款额定工况下,交直轴耦合项电压随着交直轴电流的变化情况,如图2所示。在电感参数变化的情况下,交直轴的耦合项电压变化幅度最大达到40%,最小达到−33%。因此对于前馈补偿解耦来说,唯有克服电感参数的变化才能实现精确的线性解耦控制[11],才能实现Id和Iq的最佳匹配控制,获得最佳转矩输出特性[12]。

图2 额定转速下,交直轴耦合项电压随交直轴电流变化情况Fig.2 Block Diagram of d−q Axis Coupling Voltage During Inductances in Dynamic and Steady−State
3 基于DDPG的车用电机定子电流优化控制方法
基于强化学习理论实现IPMSM定子电流优化控制系统主要包括三部分:Agent:产生控制电压;Environment:产生各种目标信号,包括间接观测量转矩、直接观测量交直轴电流等;Reward:根据Environment中反馈的Observation信息产生即时奖赏值。
3.1 状态集描述
对于电机控制来说,核心是转矩控制,决定转矩大小的是Id和Iq,任意工况下目标变量Id和Iq根据参考值和目标值的关系共存在四种状态,如表1所示。所有可能的状态S1,S2,S3,S4构成了电机控制的有限状态集S。
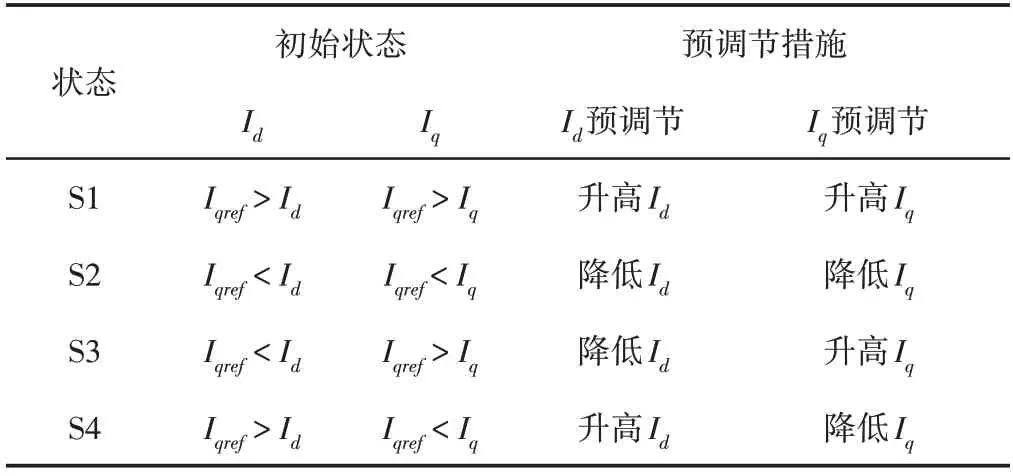
表1 交直轴电流四种状态及预调节措施Tab.1 Four States of D-Q Axis Current and Pre-Conditioning Method
3.2 动作集建立
Agent根据Environment反馈的Observation和Reward产生当前周期的Action,即ud和uq。其中Observation和Reward是对上一个周期Agent输出的Action的评价,如此迭代最终获得最佳的ud和uq输出。为了获得最佳的ud和uq需要综合考虑Id和Iq的误差、转矩、转速以及电机参数等因素,全工况内的ud和uq构成整个动作集。
3.3 奖惩函数建立
根据强化学习的机制,Agent产生的动作作用于Environment中是产生了积极的作用还是消极的作用需要一个评价机制来定义。交直轴即时奖励信号定义为:
其中,errorLimit—电流误差控制精度限制值,根据实际控制需求设定。
3.4 DDPG算法及参数更新
对于离散系统来说,控制的目标是在有限的离散时间T内达到需求的控制效果。对于前后两个时刻控制变量存在如下关系,如(4)所示。
DDPG算法的基本架构是Actor−Critic架构,在搭建策略函数π和价值函数Q的过程采用单神经网络模型分别构建Actor网络和Critic网络。在DDPG算法中,输入为当前的状态s,输出为确定性的动作值a,动作值函数Q(s,a),构建贝尔曼方程:
DDPG算法的目标函数被定义为折扣累加奖励的期望,即:
为了找到最优确定性行为策略π*,等价于最大化目标函数J(π)中的策略。
(1)Actor 网络及参数更新
动作网络的输入状态变量定义为s,Actor网络的作用是产生控制器的控制策略π。对于电机控制来说,在k时刻产生的控制策略即直轴电压ud(k)和交轴电压uq(k),因此Actor网络的实际输出可以描述为式(8):
选用基于贝尔曼方程误差的二次函数作为最小化目标函数,如式(9):
基于链式求导法则对目标函数进行求导,得到Actor网络的更新方式(10):
(2)Critic网络及参数更新
为了稳定闭环系统以及最小化成本函数,使用Critic网络实现长效最小化成本函数J(k),由此构建基于贝尔曼方程的误差函数和成本函数:
选用基于贝尔曼方程误差的二次函数作为最小化目标函数,如式(12):
使用标准的基于梯度下降的自适应方法更新Critic输出网络的权重,如式(13):
4 实验验证
为了验证所提出的基于DDPG的定子电流优化控制方法的有效性,在台架上验证了方法的有效性和可行性。整个测试实验系统由IPMSM、MCU、测功机、功率分析仪及其配套设备组成,电机试验台架的结构,如图3 所示。控制IPMSM 的上位机采用VECTOR系列的CANape软件进行控制端与MCU之间的数据通信,并记录IPMSM的相关数据以用于后续的数据分析。

图3 台架实验结构图Fig.3 The Structure of Motor Test Bench
首先,测功机以额定转速加载,对被测电机控制器施加不同的定子电流,观测被测电机的最大转矩输出。当系统稳定后,当转矩波动小于3N·m,通过功率分析仪记录最大的转矩以及通过上位机监控系统记录交直轴电流。同时,设立基于FFCDC的最大转矩电流比控制对比实验,观测在相同的定子电流下产生转矩的情况,将两种控制方法的结果汇总,摘取有限个数据点,如表2所示。

表2 传统FFCDC与DDPG实现最大转矩输出和最优Id和Iq试验数据对比Tab.2 TheExperimentResults of DDPG-NDC and FFCDC
对表2中的数据进行分析可以看出,基于DDPG的定子电流优化控制产生的最大转矩输出能力在同等Is情况下明显高于FFCDC 控制方法,最高高出20.53%,最低高出4.83%,平均高出13.36%左右。在寻找最优Id和Iq方面,基于DDPG的定子电流优化控制方法能更大限度的优化Id和Iq的匹配值,更加充分的发挥电机的效率。
对电机全工况区域分析可以看出,DDPG能尽可能的减少Id的分量,同时尽可能的提高Iq的分量以此保证产生更大的转矩输出。由此,进一步验证了基于DDPG能保证更多的定子电流分量用于产生转矩,降低励磁电流的分量,增大转矩电流的分量,体现了其优化最佳交直轴电流匹配的能力。
其次,为了进一步验证基于DDPG定子电流优化控制方法在提升电机效率方面的贡献,分别对基于DDPG 和FFCDC 两种控制方法在电机全工况区域内的电机的工作效率进行测定,获得相应的效率MAP图,如图4所示。
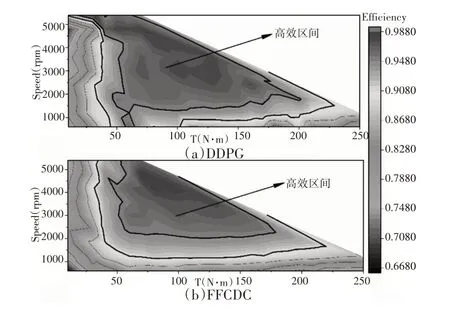
图4 全工况区域内DDPG与FFCDC效率MAP对比Fig.4 Comparison of DDPG and FFCDC Efficiency MAP in Whole Operating Area
由图4可以看出,总体来说基于DDPG获得的效率MAP图的高效工作区间要大于基于FFCDC获得的高效工作区间,体现了其在提升电机工作效率方面的优势。对比图4中的图(a)和图(b)还可以看出在电机中低转速区间内,基于DDPG的效率要高于基于FFCDC的效率,进一步体现了采用DDPG在克服低速区间电机强耦合特性对交直轴电流优化匹配的影响,更好的发挥电机的性能,提升电机整体的工作效率。
综上,台架验证了所提出的定子电流优化控制方法的有效性,不对IPMSM的交直轴电流进行解耦的情况下规避了永磁同步电机强耦合特性造成的解耦效果不佳的问题。试验数据表明DDPG相比传统的FFCDC在优化交直轴电流匹配和最大转矩电流比输出上表现地更具优势,更能充分的发挥电机的性能,产生更大的转矩输出。
5 结论
为了实现IPMSM交直轴电流最优匹配,提升IPMSM的最大转矩电流比和工作效率,提出了一种基于DDPG的车用电机定子电流优化控制方法,在不对交直轴耦合项电压进行补偿解耦的情况下实现对IPMSM交直轴电流的最优匹配控制。结果表明,基于DDPG的电机控制在优化交直轴电流匹配和最大转矩电流比控制方面优势显著,相比较传统的解耦方法在同等定子电流产生转矩输出平均高出14%。基于DDPG的控制方法能产生更大的转矩输出,更加充分发挥电机的性能,提升电机的效率。
