基于证据理论的传动方案决策系统设计
2023-03-19王红军汪润鸿李锦慧刘伟良
王红军,汪润鸿,李锦慧,刘伟良
(华南农业大学工程学院 南方农业机械与装备关键技术教育部重点实验室,广东 广州 510642)
1 引言
智能化是提高农机设计水平的重要发展方向。如何快速的从现有的多个近似传动方案中选择出符合要求的最佳方案成为当前实现拖拉机变速箱智能化设计的重要问题[1],传统的变速箱传动方案决策通常只考虑几个主要的参数(如额定功率,额定转速等)完成方案的选择,而当面对几个近似方案时,则无法选择出最佳方案。近年来,基于证据多属性方案决策理论与模型得到了极大的完善[2−6],并在故障诊断[7−8],方案评价[9−10]与信息融合[11−12]领域得到了广泛的应用。在变速箱传动方案设计过程中,为了辅助设计者在多个近似的变速箱传动方案中快速决策出最佳方案,构建了基于证据理论的拖拉机变速箱传动方案的决策系统,系统在充分考虑决策者的偏好的同时,综合考虑方案的各个属性,可实现变速箱近似传动方案的快速决策。
2 变速箱传动方案决策系统构架
在拖拉机的智能化设计中,传动系统的智能化设计是关键的一环,而在传动系统中变速箱的传动方案直接决定着传动系统的性能,实现变速箱传动方案的智能决策,是实现拖拉机智能化设计不可避免的。
2.1 系统结构及原理
遵循变速箱传动设计流程,构建了变速箱传动方案决策系统的组成模块,如图1所示。该决策系统包括人机交互模块、基础概率分配模块、权重分配计算模块以及证据加权融合决策模块传动方案库与属性概率分配规则库。人机交互模块主要是决策者的选择要求数据输入,属性偏好情况输入以及决策结果的数据展示;基础概率分配模块完成从方案库中粗选出基本符合选择要求得待选方案和完成各方案在详细选择要求下的基础概率分配;权重分配计算模块主要是将属性偏好与决策者主观权重完成结合,计算出各方案的主观权重;利用待决策方案的各属性之间的关系完成客观权重的计算;以及将主观权重与客观权重相结合,计算出最优的各属性综合权重;证据加权融合决策模块主要是利用综合权重对基础概率进行加权平均,求得新的决策证据;以及利用D−s证据理论中的组合规则实现融合决策;传动方案库是一个储存所有待选方案的数据库,为整个决策提供数据支持。
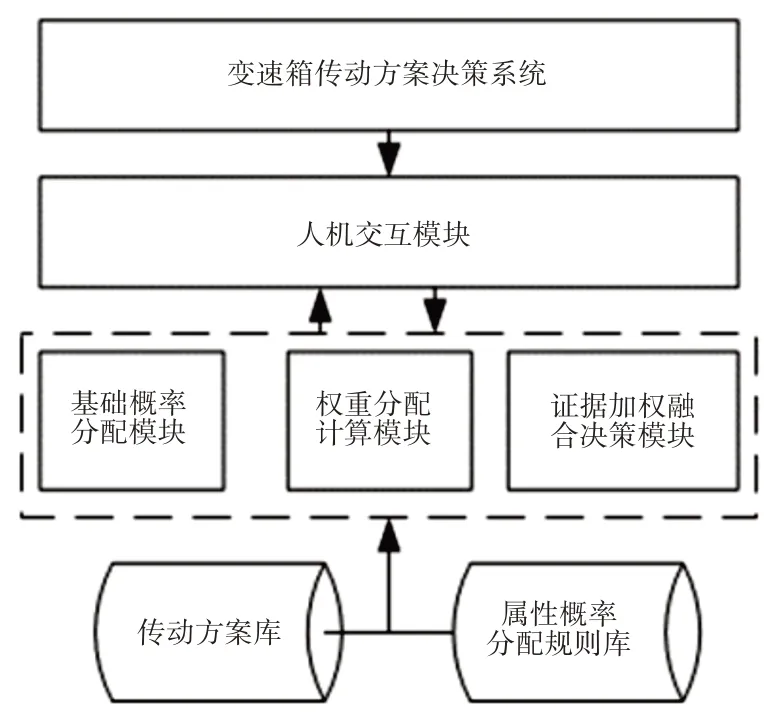
图1 系统模块组成Fig.1 System Module Composition
2.2 传动方案决策流程
变速箱传动方案决策系统的决策流程,如图2所示。决策步骤如下:

图2 系统决策流程图Fig.2 System Decision Flow Chart
(1)决策者直接设置要挑选方案的数据要求,同时对方案的主要属性(即动力性,经济性与结构性)设置偏好权重,对主属性下的各子属性分布设置偏好程度,构建各自的模糊偏好矩阵;
(2)根据选择的数据要求,从方案库选出符合要求的备选方案;
(3)依据模糊集理论与基础概率分配规则库,对待决策方案分配初始概率,求得初始基础概率矩阵;
(4)根据层次分析法原理与模糊偏好矩阵,求出本次决策的属性主观权重;
(5)在初始基础概率矩阵中计算各属性之间距离与相似度;
(6)依据相似度,求得矩阵各属性的支持度,进行归一化后,求得属性的客观权重;
(7)依据博弈论思想,结合主观与客观两个权重,求得最佳的综合权重;
(8)利用加权平均法,对初始基础概率矩阵进行加权,求得新的加权平均证据;
(9)利用D−s组合规则,对待新的加权平均证据进行次组合,依据最后的组合结果,对待决策方案进行排序,并指出最佳方案。
3 传动方案决策系统中的关键技术
3.1 基础概率分配
基于证据理论的传动方案决策系统中,待选方案各属性的基础概率是决策基石,直接影响着决策结果,文中依据传动方案各属性特点,将其进行了归纳分层,其分类结果,如图3所示。

图3 传动方案属性分类Fig.3 Transmission Scheme Attribute Classification
将14个属性分成3个大类,以便于进行属性之间对方案的影响程度对比,其中在轴承类型与换挡机构类型这两个属性作了特殊处理,在经济性与结构性中都有。
这是由于这两个属性具有一定的特殊性,例如在选择是否选择啮合套作为换挡机构时,单从经济性上进行考虑,由于其结果简单,加工制造成本低,那么肯定是优选,但从换挡的平稳性与可靠性等结构性能上考虑,由于其自身存在的换挡冲击,不易换挡等缺点,啮合套又成了劣选;同一个选择,从不同的方向考虑得出完全不同的结果,因此在文中将换挡机构类型与轴承类型这两个属性,依据在经济性与结构性下优劣特点,分别构建基础概率分配函数。利用三角模糊数、梯形模糊数、区间数以及二元语义等理论知识,结合传动方案各属性的特点,对各属性构建了基础概率分配规则,组成了属性概率分配规则库。额定功率C11、额定转速C12、输出最大扭矩C16、功率损失率C17以及油耗损失率等属性利用三角模糊数构建分配函数,计算方式如式(1):
式中:x—在Ci属性的选择要求值;a,c—允许选择的下、上限值;b—待选方案在Ci属性上的准确值;ω—可以给出最高概率,取ω=0.95。
零件个数C22、外形体积C31以及安装中心距C32等属性采用梯形模糊数构建基础概率分配函数,依据各属性的特点,以待选方案在该属性下的具体数值设置允许选择的范围(a1,d1)以及最大概率的允许范围(b1,c1),计算方式,如式(2)所示:
式中:a1,d1—允许选择的下、上限值;b1,c1—基础概率为最大值的下,上限值。
采用两区间数之间的距离为依据,构建了前进速度范围C13、后退速度范围C14、传动比范围C15以及传动效率范围C23等具有区间性属性的基础概率分配函数。假设,为同一属性下的区间数,那么两者之间的距离计算公式如式(3)所示;并且以设计要求的范围跨度的为1/3阈值,距离越小则选择的基础概率值越大,反之则越小,当超过阈值则基础概率为0。
利用二元语义的理论,对轴承类型C24,C33与换挡机构类型C25,C34两个属性分别构建了语言评价等级;计算方案的评价语言词组与选择要求的语言词组的距离,依据其距离的大小得到其偏好基础概率,距离越小,偏好概率值则越大,反之则越小,并且同时依据待选方案的该属性评价语言词组在语言评价等级中位置,求得其客观基础概率,取偏好基础概率与客观基础概率的平均值作为待选方案在该属性下的基础概率。
轴承类型C24的语言评价集为=(h1,h2,h3,h4,h5,h6)={滚针轴承,角接触滚子轴承,调心滚子轴承,圆柱滚子轴承,深沟球轴承};C33的语言评价集为在结构性中的语言评价集为=(h1,h2,h3,h4,h5,h6)={深沟球轴承,圆柱滚子轴承,角接触滚子轴承,调心滚子轴承,滚针轴承};换挡机构类型C25的语言评价集为=(h1,h2,h3,h4)={增力式同步器,惯性式同步器,常压式同步器,啮合套};C34的语言评级集为=(h1,h2,h3,h4)={啮合套,惯性式同步器,常压式同步器,增力式同步器}。假设(Hi,α)j,(Hj,α)j为一个语言评价集中的任意两个二元语义,则两者之间的距离计算公式如下:
Δ−1函数的表达式如下:
3.2 权重分配
在变速箱传动方案决策系统中属性权重分为三个部分,(1)依据由决策对方案各属性的偏好程度构建的偏好矩阵,利用层次分析法计算出的属性主观权重;(2)依据待决策方案经过基础概率分配后的基础概率矩阵,利用各属性之间的距离计算出的客观权重;(3)采用博弈论思想,结合主观权重与客观权重计算出的综合权重。
3.2.1 主观权重的分配
在构建的系统中,决策者需对三个大类设置权重,以及对每个大类下的属性设置重要程度;这种方式既可以让决策者可以很好的宏观把握对方案属性的偏好,又避免需要细致的对每个属性设置权重的繁琐。假设(n×n)矩阵A是一个大类的属性重要程度对比的判断矩阵,则其中的元素aij则表示第i个属性与第j个属性的重要程度对比。采用最常使用的比较标度,如表1所示。

表1 常用的比较标度Tab.1 Commonly Used Comparison Scales
同时,将数值2、4、6、8作为1、3、5、9对应重要程度的中间程度,而且矩阵A满足以下条件aij>0;aij=1/aji;aii=1。通过计算矩阵A的最大特征值对应的特征向量,再经过归一化处理,然后再乘以当前大类的权重即可求得该类下各属性的主观权重值。
3.2.2 客观权重的分配
在系统中的客观权重是由待选方案的基础概率决定的。设mi与mj是由待选方案在Ci属性与Cj属性下的基础概率,经归一化后构成的两条向量,即在传动方案决策模型下的两条证据,则其两者之间的距离如式(7)。
利用各属性证据之间的距离,计算其相似度,其计算公式,如式(8)所示。
从相似度计算公式可以看出,当距离越小时,相似度越大;由所有的相似度组成一个n阶的相似度矩阵,如式(9)所示。
从相似度矩阵中可以得出,若将矩阵中的某一行的相似度进行叠加,则可以得到其他证据对该证据的总相似度,把这种总相似度称之为支持度,其计算方式,如式(10)所示。
证据之间的支持度直接反映了证据对于待决策方案的重要程度,因此对所有的支持度进行归一化处理即可求得待决策方案各属性客观权重ω',客观权重分配的计算方式,如式(11)所示。
3.2.3 综合权重的分配
利用博弈论中均衡解的思想,将由层次分析法求得的主观权重与利用待决策证据之间的支持度求得客观权重相结合,求解出既考虑了待决策属性的客观性,又考虑了决策者的主观性的综合权重。设集合ω={ω1,ω2,…ωL}为L个权重向量组成的权重集合,对于该集合可以中各向量可以随意的进行线性组合,如式(12)所示。
为了获得最优综合权重,故对上式中的ai优化,使得ω与ωi的离差最小化。其数学表达式,如式(13)所示。
根据矩阵的微分性质,上述表达式的最优化一阶导数符合式(14):
根据式(14)可以求出a=(a1,…,aL),然后对a进行归一化处理,其公式,如式(15)所示。求得最佳的权重系数a*;从而求得最佳综合权重ω*,其计算公式,如式(16)所示。
3.3 加权融合规则
在构建的系统中,先利用综合权重对基础概率矩阵进行加权平均,得到新的证据,再采用证据理论的组合规则对新的证据进行n−1组合,从而实现方案的决策。加权平均的计算方式如式(17):
式中:M'(m)—加权后的新证据
设m1与m2同为框架Θ下的两个基本概率分配函数,则利用组合规则可以使用m表示m1与m2合成后的新证据,其组合规则的计算方式,如式(18)所示。
式中:k—冲突系数,计算公式如式(19);Ai,Bj—识别框架中的焦元。
4 系统算法测试
为验证决策系统算法的有效性,对系统进行了验证测试。以某一次传动方案选择的数据为测试实例,具体测试数据,如表2所示。

表2 测试数据Tab.2 Test Data
设置主因素的权重w0={0.5,0.3,0.2},经专家人工分析计算得出决策结果是M={E1,E2,E3}={0.8814,0.1103,0.0083}
认为方案E1是符合选择要求的最佳方案。同时采用相同的选择要求,设置相同的权重与偏好以及相同的数据对决策系统进行验证;选择要求输入界面,如图4所示。在该界面中输入决策者对方案的要求数据。

图4 选择要求输入界面Fig.4 Select Required Input Interface
系统的权重输入界面,如图5所示。在该界面中决策输入主因素的权重值以及对方案各属性的偏好。系统的决策结果界面,如图6所示。展示了参与决策方案的基本信息、求得的权重数据以及决策的结果;决策系统得到结果为:M={E1,E2,E3}={0.8881,0.1097,0.0022},与人工分析求得结果M={E1,E2,E3}={0.8814,0.1103,0.0083},相比较,各待选方案的决策得分分别相差0.0067,0.0006,0.0061,验证了变速箱传动方案智能决策系统的算法的有效性。

图5 权重输入界面Fig.5 Weight Input Interface

图6 决策结果界面Fig.6 Decision Results Interface
5 结语
通过构建传动方案决策系统,有效的解决了多个近似变速箱传动方案的融合决策问题,对大型拖拉机传动系统智能化设计进行了有效的补充。使用模糊集理论将变速箱的各属性的描述有效的转化成了决策基础概率,采用综合权重对基础概率进行加权,不仅充分考虑了决策者的主观意识,也考虑率了待选方案之间的相互关系,利用证据理论对加权后的新证据进行了有效融合。经实例验证表明,该系统的决策结果与专家决策结果基本保持一致,所提出的算法可用于变速箱传动方案的智能决策系统中,具有一定应用价值。
