薄煤层采煤机摇臂行星传动齿轮优化设计
2023-03-19慕杰翟雨生王成志高振帮
慕杰,翟雨生,王成志,高振帮
(1.煤炭科学研究总院,北京 100013;2.天地上海采掘装备科技有限公司,上海 201400;3.江苏徐矿能源股份有限公司,江苏 徐州 221600)
1 引言
煤炭是我国的基础能源,也是重要的工业原料。随着采煤机械化迅猛发展,十几年来,我国煤炭年产量不断创出新高,各大矿区易于开采的中厚煤层储量不断降低,薄与极薄煤层所占比重越发增加[1]。为避免资源浪费,实现煤炭资源均衡开采,许多矿区均加大了对薄与极薄煤层的开采力度。薄煤层由于采高低,开采劳动强度高,工作条件恶劣,为保证生产效益必须实现高效开采,客观决定薄煤层采煤机向高功率密度方向发展。
行星传动齿轮系统具有结构紧凑、质量小、承载能力大、能量密度高、传动效率高等诸多优点,被广泛应用于矿山、海洋等重型工程机械装备中[2]。薄煤层采煤机由于采高低,配置较小直径滚筒,为保证良好的装煤效果,滚筒内部行星传动齿轮的径向尺寸受限[3]。由于我国薄煤层特殊的地质条件,采用窄截深开采,行星传动齿轮的轴向尺寸受制于机身和开采深度。上述诸多客观因素,严重制约薄煤层滚筒式采煤机高功率密度化发展的进程。在保证采煤机运行可靠的前提下,对其摇臂行星传动齿轮系统进行优化设计,有着重要的工程实践意义。
传统采煤机设计过程中,研发人员只对摇臂行星齿轮的接触、弯曲疲劳强度进行简单校核;安全系数的选取主要采用经验数据,存在设计裕量过大、设计不精细等不足之处。中厚煤层采煤机体型大、散热快、开采条件好,受传统设计的影响较小,但该方法不利于高功率密度的薄煤层采煤机的现代化设计。为更好解决传统设计的不足,实现低采高、小体积、高功率密度的特点;现以某型号薄煤层采煤机内部NGW型行星传动齿轮为例,以行星传动齿轮总体积为目标函数,建立传动系统结构的数学模型,充分利用现代优化设计理论与方法,对其进行优化求解和研究。
2 优化数学模型的建立
某型号薄煤层采煤机摇臂齿轮传动工作原理,如图1所示。齿轮Z2、Z5、Z6为惰轮,其余均为啮合齿轮。NGW型行星减速器通过花键与末端直齿轮Z7联接,实现了传递大功率、承受复杂载荷、将动力经减速传递给滚筒的重要作用。

图1 摇臂齿轮传动系统工作原理Fig.1 Working Principle of Rocker Gear Transmission System
该款NGW型行星传动齿轮为四行星轮减速机构,主要由太阳轮、行星轮、内齿圈、行星架等组成。其传动结构,如图2所示。传统经验设计基本参数,如表1所示,具有如下特点:

表1 NGW行星传动齿轮基本参数Tab.1 Basic Parameters of NGW Planetary Transmission Gear

图2 NGW型摇臂行星传动齿轮结构Fig.2 NGW Type Rocker Arm Planetary Transmission Gear Structure
(1)为保证良好的装煤效果,控制径向尺寸;同时使减速系统受力均衡,为太阳轮自动定心,拟采用4个行星轮啮合。
(2)为满足4个行星齿轮的均载特性,太阳轮采用浮动结构;可沿轴向灵敏地浮动,减小反向力矩,通过与大齿轮相配合的外花键侧隙来保证其轴向浮动量。
(3)太阳轮受力转动时,驱动行星轮沿各轴线自转,同时带动行星架转动;行星架通过花键和方形套联接,将输出转矩传递至滚筒。
滚筒式采煤机在截割煤岩时,行星减速机构承受复杂的冲击载荷。太阳轮齿数少、直径小,所受载荷循环次数最多,行星轮受内、外双向弯曲载荷。
太阳轮和行星轮选用相同材质的优质合金钢18Cr2Ni4WA,进行渗碳、淬火、磨齿、强化喷丸等多工序处理,提高接触与弯曲疲劳强度。内齿圈的强度和硬度可适当降低,选用高强度钢42CrMo,插齿后深层氮化处理。
2.1 确立设计变量
通过分析,选取对设计指标有影响、且能独立控制的相关参数作为设计变量,其余作为常量处理[4]。通常情况下,行星轮和内齿圈的齿数受到配齿条件制约,行星齿轮个数确定后,NGW行星减速器的体积取决于太阳轮齿数ZA、内齿圈齿数ZB、行星轮齿数ZC和齿宽b、模数mn;即上述参数相互约束、共同作用,则有设计变量x:
2.2 建立目标函数
本研究中对行星传动齿轮的优化设计目标为:相同载荷下总体积最小,故选取行星齿轮减速器体积作为优化目标函数。NGW型行星齿轮机构的体积即太阳轮、内齿圈及CS个行星轮体积之和,经化简整理,得优化设计目标函数为:
式中:VA、VB、VC—太阳轮、外齿圈、行星轮体积,单位mm3;CS—行星轮个数,此处取值为4;x2—齿宽,单位mm;x3—模数;x1、x4、x5—太阳轮、外齿圈、行星轮齿数。
2.3 选取约束条件
优化设计目标函数为(1),以行星传动齿轮中最薄弱的太阳轮为例,建立约束条件如下:
2.3.1 边界约束条件
(1)齿轮采用范成法加工,为保证太阳轮齿轮zA不发生根切现象,当=1,α=20°时,有:
(2)装煤要求制约了行星齿轮的径向尺寸,在保证齿轮接触强度和弯曲强度的前提下,应增加轴向尺寸,即增大齿宽系数。但齿宽系数过大,将增大载荷沿接触线分布的不均匀程度,故齿宽系数应选择适当[5],即0.7 ≤ϕd≤1.5:
(3)设计模数优先选用第一系列[6],限制最小值为2,得:
(4)限制齿宽最小值为150mm,得:
(5)限制行星传动系统最低传动比i为5.2,得:
(6)参照文献[6]齿面接触强度公式可得:
式中:Ad—计算接触强度的相关系数,直齿轮啮合时值为766,该行星机构中太阳轮和行星轮材质均为18Cr2Ni4WA,属于高强度中合金渗碳钢,故修正后的相关系数为:0.997Ad;TA—太阳轮的输入转矩,单位Nm,计算如下:
(7)根据齿根弯曲疲劳强度公式得:
式中:Am—计算齿根弯曲强度的相关系数,直齿轮啮合时值为12.60;σHlimb—齿轮弯曲疲劳极限应力,取σHlimb=420MPa;YF—齿形系数,即复合齿廓系数,近似值取YF=3.10。
整理可得,约束条件为:
2.3.2 NGW型行星齿轮配齿约束条件
行星齿轮传动各齿数的选择,除了应满足渐开线圆柱齿轮齿数选择的原则,还应满足同心条件、装配条件和邻接条件。
(1)同心条件
对于NGW型传动,为保证准确传动比,各对啮合齿轮之间的实际中心距必须相等[6],故有:
(2)装配条件
各行星轮能均布安装且与中心轮啮合良好,太阳轮与内齿圈的齿数之和应为行星轮个数的整数倍,即:
(3)邻接条件
相邻两行星轮互不相碰,行星轮齿顶圆半径之和小于中心距,即:
综上所述,该问题为一个具有5个设计变量,7类边界约束条件和3个关联条件组成的复杂优化设计模型。
3 优化方法
3.1 基于非线性规划的优化方法
fmincon函数是MATLAB优化工具箱中求解非线性规划问题的函数,根据有无梯度表达,对目标函数选择大型或中型算法,从一预估值出发,搜索约束条件下非线性多元函数的最小值[7−8]。上述模型的约束条件中无梯度表达,适配中型算法,函数调用格式为:[x,fval,exitflag,output]=fmincon(fitness,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)。
其中,fitness为目标函数;初值x0为满足约束条件的任意解,所选初值会影响fmincon函数,导致求得局部最优解,故选用原始设计点,即x0=[x1,x2,x3,x4,x5]=[ 17,175,9,83,33 ]。
太阳轮、外齿圈、行星轮齿数分别为17、83、33,齿宽175mm,模数9。A、b、lb、和ub 为线性不等式约束系数和上、下界向量;Aeq和beq为等式约束条件的等式约束的系数矩阵[7],其余参数的含义及调用方法在此不做赘述。
3.2 基于遗传算法的优化方法
遗传算法(Genetic Algorithm,GA)是模拟Darwin生物进化论和Mendel的遗传学说,借鉴自然选择和遗传学机理的全局随机搜索算法,直接对结构对象进行操作,具有较强的智能性、鲁棒性、良好的可操作性等优点[9−10]。
其处理问题的一般流程,如图3所示。MATLAB中遗传算法的主函数为ga,该函数的功能为利用遗传算法求函数的极小点,调用格式为:[x,fval,exitflag,output,population,scores]=ga(fit⁃ness,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)。

图3 遗传算法的程序框图Fig.3 Block Diagram of Genetic Algorithm
以上调用的遗传算法工具箱中需要输入的参数包括:计算适应度函数的函数句柄@fitness、适应度函数中变量个数nvars、优化参数结构体options等,输出最终返回点x、适应度函数在x点的值fval、优化终止的状态指示结构变量exitflag、算法每一代的性能output、以及最后评价得分值scores等[7]。
对于上述问题,考虑到1.3节建立数学模型的复杂度等,设置初始种群大小n为500,交叉概率Pc为80%,变异概率Pm为10%,终止算法的迭代次数为500次。
3.3 优化结果处理与分析
上述研究中,例如齿数、模数等设计变量为整数,前期优化设计中均作为连续变量处理,在得到满足条件的最优解后,还需要进行圆整处理。针对该问题,处理过程如下:所求未经圆整处理的最优解构成解集为,分别对其进行圆整,可得到距离其最近的两点,故至多可得到25个整型解[4]。对所有整型的解,均需带入优化目标函数即体积函数中进行对比计算,从而得到满足数学模型和实际工况的最优整型解。
通过MATLAB 优化工具箱进行求解,按国家标准对优化设计结果进行圆整、对比计算,最终可得满足优化设计数学模型的函数解与常规设计对比分析结果,如表2所示。
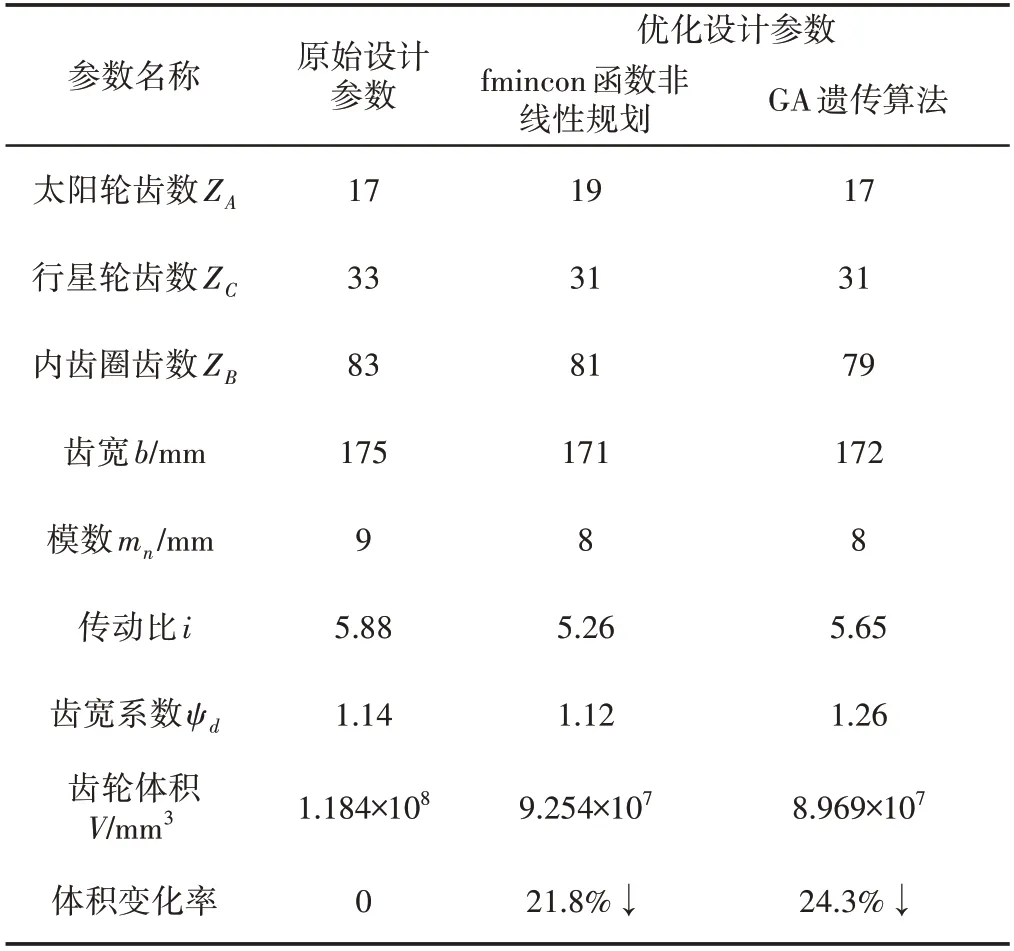
表2 NGW型行星传动齿轮最终优化结果参数Tab.2 The Final Optimized Parameters of NGW Lanetary Transmission Gear
分析表2可得,经过fmincon函数非线性规划和遗传算法优化,NGW型行星传动齿轮齿数、传动比均有微调,总体积较原设计分别减小21.8%和24.3%。上述优化设计过程表明,基于fmin⁃con函数非线性规划和遗传算法的行星传动齿轮优化设计,能够达到减小体积,提高功率密度的设计目标;遗传算法相比非线性规划方法在寻找全局最优解方面更有优势。
4 结论
采煤机摇臂传动系统设计是一个多变量、多约束条件、多目标优化的复杂问题。为改善NGW 行星传动齿轮传递功率大,承受载荷复杂的恶劣工况,从而适应低采高、小体积、高功率密度的工作特点;建立以缩小行星传动齿轮总体积为优化目标,在保证采煤机运行可靠的前提下,以齿面接触强度、齿根弯曲强度等7类边界约束条件和同心、装配、邻接等3个关联条件组成的优化设计数学模型。基于MATLAB 中fmincon 非线性规划和遗传算法,分别对上述数学模型求解,并按照国标对所得结果进行圆整后处理。
所得优化结果较常规设计有显著提高,能够进一步缩小体积、降低成本,增大功率密度,提高薄煤层采煤机对井下恶劣工况的适应性。该研究为薄煤层采煤机摇臂行星传动齿轮的优化设计提供了理论依据,具有一定的工程实践意义。
