滚刀刀圈轧制工艺参数的家族遗传算法优化
2023-03-19李奕晓杨善国王旭荣
李奕晓,杨善国,王旭荣
(1.永城职业学院机电工程系,河南 永城 476600;2.中国矿业大学机电工程系,江苏 徐州 221004;3.山东交通职业学院,山东 潍坊 261206)
1 引言
盘形滚刀是岩石掘进机(Tunnel Boring Machine,TBM)的关键部件,在TBM掘进工作过程中,滚刀刀圈直接与岩石接触,刀圈的产品质量直接影响岩石掘进机的破岩效率和破岩成本。低质量的刀圈在破岩过程中磨损较快、刀圈更换过于频繁,从而降低TBM的破岩效率并提高破岩成本[1]。因此,研究滚刀刀圈的成形工艺优化方法,可以有效降低TBM破岩成本、提高破岩效率。
为了提高盘形滚刀刀圈的成形质量(主要为刀圈的耐磨特性),学者们从多个角度进行了大量的研究和实验。主要包括刀圈的失效机理分析[2]、滚刀刀圈−岩石对磨缩尺比例试验台的研制[3]、滚刀刀圈的性能优化等。刀圈性能优化的途径包括调整材料合金成分、制备材料表面梯度熔覆层、改进模锻或轧制工艺等。文献[4]分析了不同材料合金成分对刀圈耐磨性能的影响,结果表明C、Cr、Mn等元素的增加可以在一定程度上提高刀圈耐磨性。文献[5]建立了基于塑性去除机制和断裂去除机制的综合磨损模型,并使用粒子群算法优化了模型参数,得到了较为准确的刀圈磨损模型,为刀圈耐磨性能优化提供了参考。文献[6]使用两种热处理工艺对DC53材料刀圈进行热处理,并对比两种刀具的晶粒度、硬度、冲击韧度等,最终得到了DC53材料刀圈较好的热处理工艺。文献[7]根据理论分析对轧制成形中的轧辊尺寸和工艺参数进行了设定,并使用实验对设定结果进行了验证。以上成果从不同角度和方向提高了滚刀刀圈的耐磨性能,从成形工艺优化的角度入手提高刀圈的质量和性能。针对滚刀刀圈轧制工艺优化,介绍了轧制成形工艺和轧制方法,建立了目标函数模型,使用家族遗传算法对优化模型进行求解,达到了提高刀圈轧制性能的目的。
2 滚刀刀圈轧制有限元分析
2.1 刀圈轧制坯料
研究对象为17in(43.18mm)滚刀刀圈,使用轧制成形方式。轧制所用材料为H13钢,即4Cr5MoSiV1模具钢,此材料的成分及力学参数分别[8],如表1、表2所示。
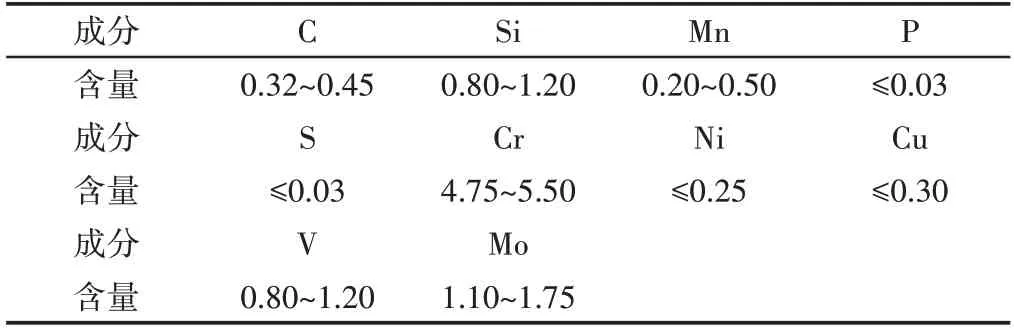
表1 H13钢化学成分(%)Tab.1 Chemical Composition of H13 Steel(%)

表2 刀圈材料力学参数Tab.2 Material Mechanical Parameters of Cutter Ring
根据17in滚刀刀圈尺寸和环形件轧制毛坯设计公式,得到用于轧制的毛坯尺寸,如图1所示。
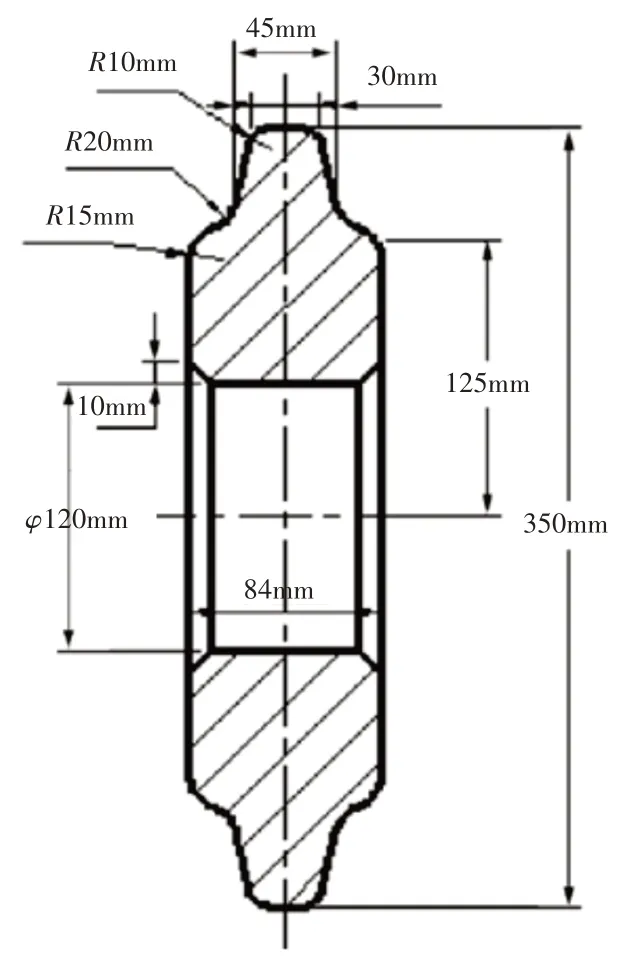
图1 轧制毛坯尺寸Fig.1 Size of Rolling Blank
2.2 轧制成形方法
滚刀刀圈的轧制成形略显复杂,主要体现在轧辊方面。滚刀刀圈中间有孔,刀圈厚度不一致,需要多个轧辊配合完成轧制过程,如图2所示。
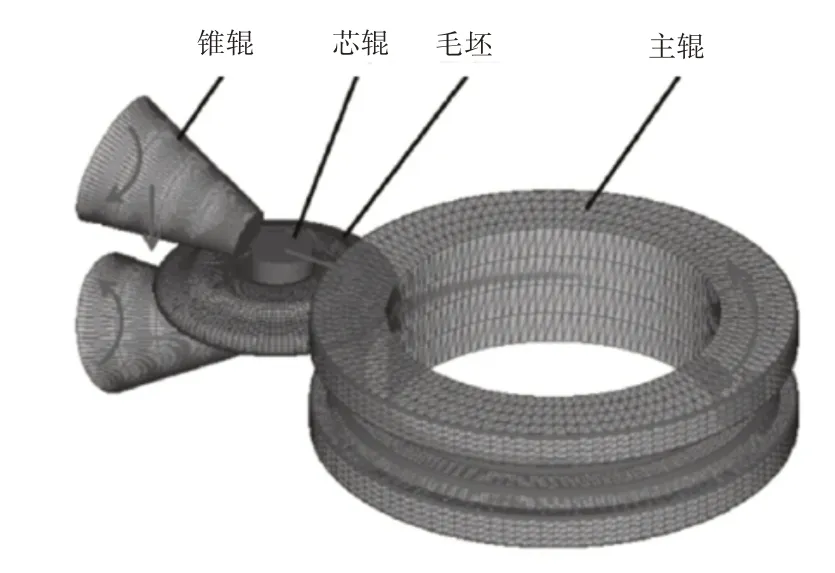
图2 刀圈轧制方法Fig.2 Rolling Method of Cutter Ring
轧辊包括主辊、芯辊和锥辊3类,芯辊为了生产出中间的孔洞,主辊和锥辊配合轧制出厚度不一致的刀圈部分。图中带箭头的红线表示各芯辊的转动方向和受力方向。
2.3 优化目标函数建立及优化参数选择
滚刀刀圈的轧制成形质量可以使用等效应力和等效应变两个参数进行衡量。坯料在成形过程中变形越均匀,局部区域的变形差异性越小则成形后晶粒越均匀,成品的靠疲劳寿命越长。
一般使用标准差描述参数的分散特性,使用等效应力和等效应变的标准差描述这两个参数的离散程度,参数的标准差越小表示成形过程的等效应力场和等效应变场越均匀,轧制成形的质量也就越好。等效应力和等效应变的标准差分别为:
式中:S1—等效应力标准差;S2—等效应变标准差;N—单元节点数量;an—第n个单元节点的等效应力;—所有单元节点等效应力的均值;bn—第n个单元节点的等效应变;—所有单元节点等效应变的均值。
根据分析,滚刀刀圈轧制优化的目标函数为:
选择坯料初始温度tin、主辊摩擦因子μ、主辊转速nzg为优化参数,具体分析如下。
(1)坯料初始温度对轧制成形影响较大,当初始温度较高时材料塑性增强,材料的变形抗力也减小,材料变形相对均匀,但是材料温度过高会出现过烧现象。当初始温度过低时,材料塑性差则材料变形抗力相对较大,金属流动性差容易导致填充不足等问题。基于以上分析,选择坯料初始温度作为一个优化参数。H13钢的锻造温度范围为(869~1156)℃,同时考虑到模具与毛坯接触后的热传导效应将H13 钢的初始温度范围设置为(1050~1200)℃。
(2)主辊摩擦因子对轧制的影响体现在:当主辊摩擦因子较大时,刀圈轧制后期主辊与毛坯接触面积变大,摩擦因子大导致金属流动困难,从而出现填充不足和应力不稳定波动等现象。当摩擦因子较小时,毛坯和主辊间在轧制过程中容易出现打滑现象,也会造成变形不均匀问题。根据生产经验将摩擦因子优化范围设置为(0.55~0.95)。
(3)主辊转速对刀圈轧制成形质量的稳定性影响较大,当主辊转速较大时,毛坯进入轧辊孔型较为困难,使轧制成形效率降低。当主辊转速较小时,毛坯容易进入孔型,但是转速过小容易形成多边形缺陷。根据主辊设计的工艺参数,将主辊转速优化范围设置为(1.84~4.21)rad/s。
3 仿真数据获取与数据回归
3.1 仿真数据获取
为了获得充分的样本数据同时节约成本,本节使用有限元仿真的方式获得实验数据。使用Brick Mesh对刀圈进行网格划分,对于网格畸变问题,使用网格自适应重划分技术进行处理。将H13钢设置为塑性体,模具全部设置为刚体。模具预热温度设置为250℃,环境温度设置为25℃,锥辊转速设置为9.6r/min,芯辊进给速度为1.3mm/s。毛坯与空气的传热系数设置为0.02N(/s·mm·℃),毛坯与模具的传热系数设置为11N(/s·mm·℃)。毛坯与轧辊间的摩擦全部设置为Shear摩擦方式,毛坯与主辊摩擦系数设置为0.7,与芯辊摩擦系数为0.5,与锥辊摩擦系数为0.3。在3维优化空间中,以随机抽样[9]的方式抽取80组采样点,按照上述仿真设置得到各采样点的刀圈轧制仿真结果,统计各仿真件的等效应力和等效应变标准差结果,如表3所示。
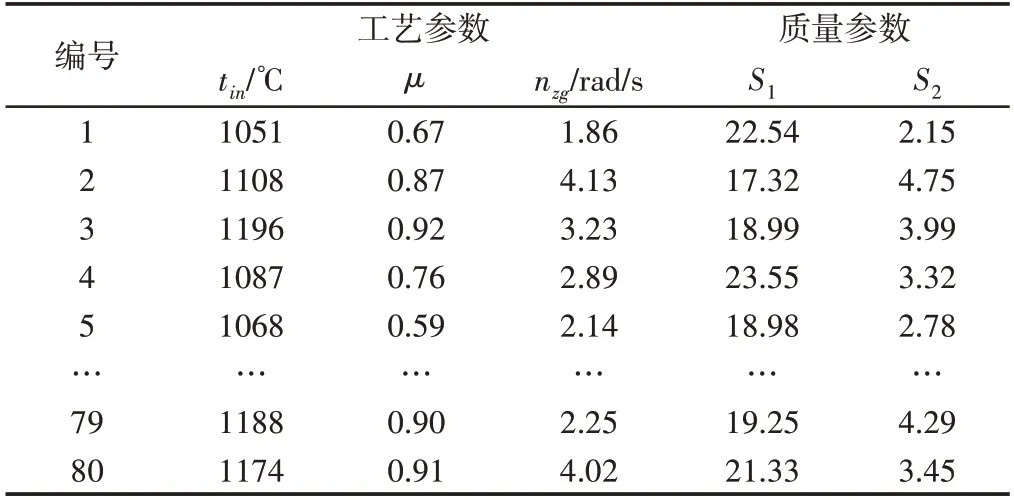
表3 仿真结果统计值Tab.3 Statistics of Simulation Result
3.2 基于自适应学习神经网络的数据回归
使用自适应学习BP神经网络进行数据回归,BP神经网络由输入层、隐藏层、输出层组成。对于两个工艺参数的优化问题,建立1个回归模型。由于选择的优化参数为3个,因此将输入层神经元数量设置为3,输出层神经元设置为1。隐藏层神经元数量的经验公式为H=+A,m1、m2分别为输入层和输出层神经元数量,A为[1,10]间的整数,将输入层和输出层神经元数量代入到公式中,最终确定隐藏层神经元数量为4。则最终的神经网络结构,如图3所示。神经网络的数据传输包括正向传播和反向训练2个过程,数据的正向传播过程即为数据的加权和神经元激活过程,具体可参考文献[10],这里不再赘述,隐藏层神经元和输出层神经元均使用Tansig激活函数。
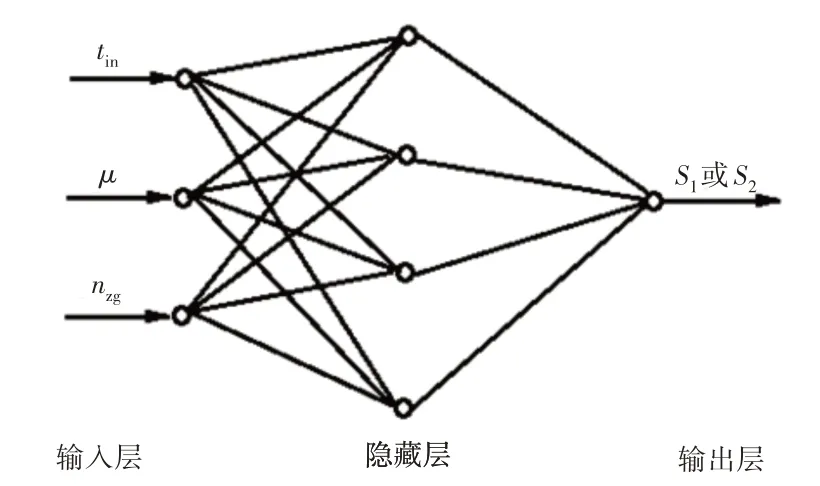
图3 神经网络结构Fig.3 Structure of Neutral Network
误差的反向传播即为参数的训练过程,将输入神经元k到隐藏神经元l的传递权值记为wkl,以wkl为例,参数的训练方法为:
式中:Δwkl(t)—迭代t次时的参数修正值;E(t)—训练t次时的训练误差;η—学习效率。
传统BP神经网络的学习效率使用固定值,但是若η较小则训练过程收敛速度慢,若η较大虽然收敛较快,但是会影响训练精度。基于以上考虑,提出了自适应学习神经网络,其思想为:当训练t+1次的误差小于t次时,说明训练效果较好,此时应增大η值,当训练t+1次的误差大于t次时,说明训练效果较差,此时应减小η值。按照以上思路,自适应学习效率为:
式中:α—自适应系数。
3.3 回归效率与预测精度验证
从80组样本数据中随机选取70组作为训练样本,剩余10组作为测试样本。将神经网络的最大训练次数设置为200次,训练目标设置为0.1,即当相对误差小于99%时训练结束。使用训练停止时的训练次数作为回归效率的评价指标,将测试样本的拟合准确度作为预测精度的评价指标。
拟合准确度定义为:
式中:Acc—拟合准确度;yu—第u个测试样本输出值;Ou—第u个测试样本拟合值。
按照上述定义,得到自适应学习神经网络与传统BP神经网络的回归效率和预测精度对比结果,如表4所示。
由表4中数据可知,BP神经网络训练187次达到训练目标,而自适应学习神经网络训练121次就达到了训练目标。BP神经网络的预测精度为93.27%,自适应学习神经网络的预测精度为98.89%,远高于传统BP神经网络。
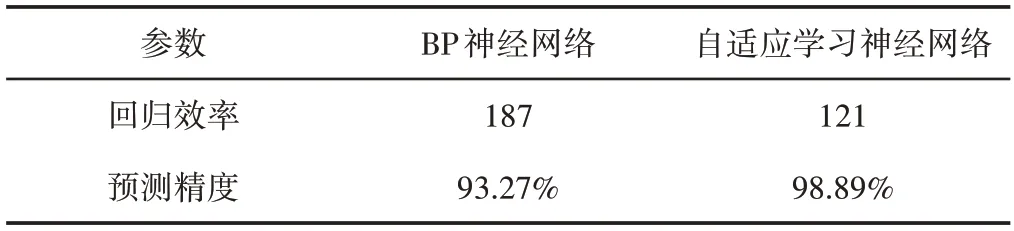
表4 两种神经网络性能对比Tab.4 Properties Comparison of the Two Neutral Networks
这是因为改进神经网络中使用了自适应学习效率因子,该学习因子可以根据训练精度自适应调整大小,既保证了训练效果好时的快速搜索,也保证了训练效果差时的细致搜索,因此其回归效率和预测精度均优于自适应学习神经网络。
4 基于家族遗传算法的模型求解
4.1 基于遗传算法的模型求解方法
使用遗传算法求解2.3节建立的优化模型,主要通过染色体编码和适应度函数的设置,将轧制参数优化问题转化为染色体进化问题。
4.1.1 染色体编码。
根据优化参数的数量,将染色体设置为3个基因位,每个基因位使用十进制实数编码,即染色体编码为(tin,μ,nzg)。第一基因位为坯料初始温度,第二基因位为主辊摩擦系数,第三基因位为主辊转速。
4.1.2 适应度函数设置。
适应度函数在遗传操作后用于评价染色体优劣,最小化优化问题,因此规定染色体适应度越小则越优。根据前文建立的优化目标函数,将适应度函数设置为:
式中:fit—适应度函数;w1—等效应力权值;w2—等效应变权值,要求w1+w2=1。上式中S1除以10后加权,是因为两个质量参数约差一个数量级。w1和w2的设置依据不同的优化重心可以设置为不同的值,两者同等重要,因此设置w1=w2=0.5。
4.1.3 染色体初始化。
使用随机方式进行染色体初始化,以主辊摩擦因子μ为例,方法为[11]:
式中:μ(0)—摩擦因子初值;μmin—摩擦因子最小值;μmax—摩擦因子最大值;rand(0,1)—(0,1)间随机数。
4.1.4 交叉和变异。
传统遗传算法按照交叉和变异概率从父代中选择参加遗传操作的个体,而后进行交叉和变异操作[12]。考虑到染色体较短,本文使用单点保留交叉方法,从(1,2,3)中随机产生一个数字,若产生的是1,则1基因位保持不变,2、3基因位交叉;若产生的是2,则2基因位不变,1、3基因位交叉,以此类推。变异使用随机变异法,即随机产生一个基因位,按照式(7)的方法随机产生一个基因值,替换掉原基因值,则实现了单基因位随机变异。
4.2 基于家族遗传算法的求解方法
传统遗传算法存在过早成熟收敛的问题,表现在算法未搜索到最优解却提前失去了进化能力。从本质上讲,是因为染色体失去了多样性,相似的染色体无法通过交叉进行有效进化。为了解决这一问题,提出了多家族遗传算法,其基本思路为:将整个种群划分为I个家族,而后进行家族内和家族间的交叉操作,具体操作如下。
(1)家族划分方法。种群初始化后,按照适应度值对染色体从小到大进行排序,适应度第1的分配给家族1,排名第2的分配给家族2,依次分配,第I个分配给家族I,第I+1个分配给家族1,如此循环往复直至将所有染色体分配完毕。
(2)家族内交叉。家族内交叉本质上是家族内算法的进化过程,规定各家族的最优个体不参与家族内交叉,其余个体进行交叉繁衍。家族内交叉操作后选择适应度小的个体保留在家族中。
(3)家族间交叉。所有家族进行随机配对,选择各家族的最优染色体进行交叉。家族间的这种交叉操作本质上避免了近亲繁殖,可以增加染色体多样性。交叉完毕后父代和子代全部回到各自家族,并将家族最差个体删除,从而保持染色体规模不变。
5 仿真与实验验证
5.1 优化过程与结果
分别使用遗传算法和家族遗传算法对刀圈轧制过程进行优化,算法的参数设置为:染色体规模为250、交叉概率为0.3、变异概率为0.05、最大迭代次数为200。在家族遗传算法中将染色体分为5个家族。两种算法对参数的优化过程,如图4所示。
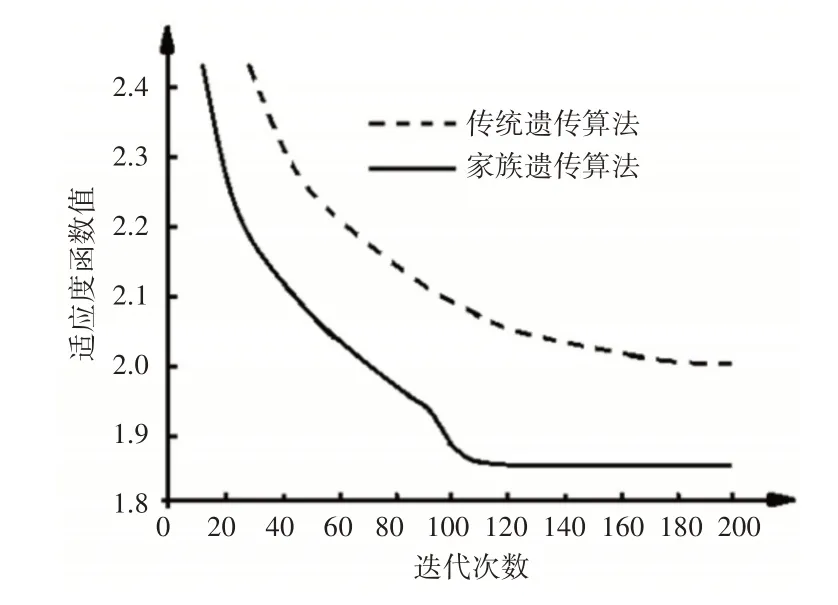
图4 算法对轧制问题的优化过程Fig.4 Rolling Problem Optimization Process of Algorithms
由图4可以看出,随着迭代的进行,染色体的适应度函数值逐渐减小,说明传统遗传算法和家族遗传算法均可以对轧制问题进行一定程度的优化。从迭代过程看,传统遗传算法迭代186次后适应度函数值不再变化,家族遗传算法迭代114次后适应度函数值不再变化,说明家族遗传算法的搜索效率高于传统遗传算法。从最终的搜索结果看,传统遗传算法的适应度函数值为2.05,家族遗传算法的适应度函数值为1.86,比传统算法减少了9.27%。这是因为家族遗传算法中使用多家族并行进化和家族间交叉交流策略,在提高搜索效率的同时维持了染色体的多样性,因此家族遗传算法的搜索效率和搜索质量均高于传统遗传算法。由于家族遗传算法的优化结果更好,所以下文对家族遗传算法的优化结果进行验证。家族遗传算法最优染色体对应的最优参数为:坯料初始温度1130℃,主辊摩擦因子0.85,主辊转速3.42rad/s。
5.2 有限元仿真验证
使用Deform−3D有限元软件对优化后的参数进行仿真验证,得到刀圈截面的等效应变,如图5所示。刀圈截面的等效应力,如图6所示。
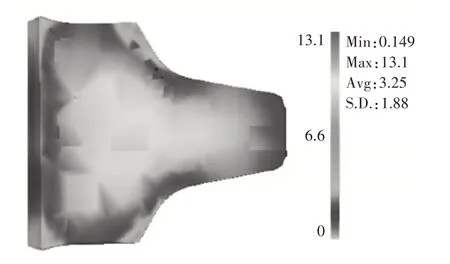
图5 等效应变分布图Fig.5 Distribution Map of Equivalent Strain
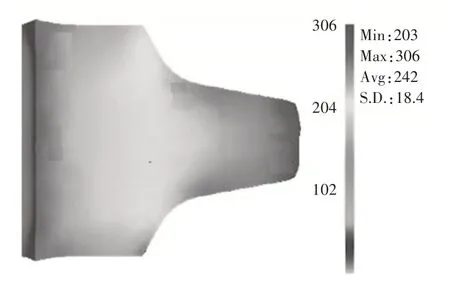
图6 等效应力分布图Fig.6 Distribution Map of Equivalent Stress
由图5可知,刀圈截面的等效应变整体分布均匀,刀圈表面与轮廓区域的等效应变相对较大,这是因为刀圈表面与模具接触,材料流动时因摩擦影响而使得等效应变较大。等效应变整体分布均匀说明刀圈晶粒组织演变均匀,轧制成形后组织性能良好。
由图6可知,刀圈截面的等效应力由表面向内芯呈现递减的趋势,无明显的应力集中,等效应力整体分布均匀。刀圈表面较大的等效应力可以提高金属致密性,在一定程度上提高金属的耐磨性能和抗冲击性能。根据仿真结果,刀圈的仿真成形结果较好,可以进一步进行实验验证。
5.3 实际生产验证
使用D53K−800数控轧环机对滚刀刀圈进行轧制,该轧环机可以轧制的环件外径尺寸范围为(350~800)mm,可轧制的环件最大高度为300mm。根据优化后的工艺参数,毛坯经真空淬火炉加热至1130℃,主辊与坯料之间的摩擦因子采用热轧油进行调节。同时为了防止随机,如图7所示。从8个轧制产品外观可以看出,刀圈轧制件无明显的裂纹、翘曲、折叠、飞边等缺陷,各角隅充型较为充分,外观检查合格,可以进一步对内部性能进行检验。从厂家当前生产的滚刀刀圈中随机选择8个与优化生产的滚刀刀圈进行比较,将刀圈轧制品进行切割得到刀圈截面,而后进行硬度检测,检测点的选择分为横纵两个方向,如图8所示。图中直线1为纵向检测点,各检测点间距为3mm,共选择11个检测点;直线2为横向检测点,各监测点间距为4mm,共4个检测点。将8个滚刀刀圈进行切割,切割面随机选取。按照图8给出的检测点测量各截面的硬度,而后取8个截面在各检测点的平均值,厂家生产的刀圈与优化后的刀圈截面硬度对比结果,如图9所示。

图7 刀圈轧制产品Fig.7 Cutter Ring Rolling Product
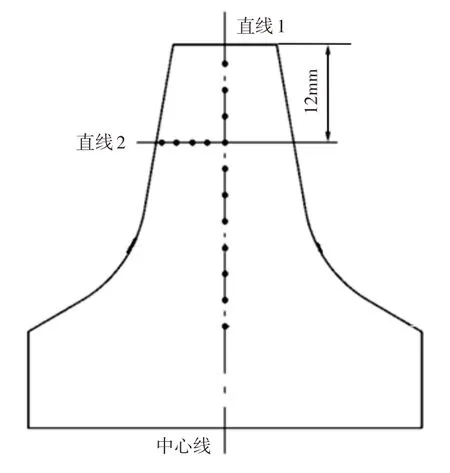
图8 硬度检测点Fig.8 Hardness Test Points
将8个滚刀刀圈进行切割,切割面随机选取。按照图8给出的检测点测量各截面的硬度,而后取8个截面在各检测点的平均值,厂家生产的刀圈与优化后的刀圈截面硬度对比结果,如图9所示。分析图9可知:(1)优化前后刀圈轧制件的硬度变化规律、分布规律大致相同;(2)优化后轧制件的硬度整体大于优化前,说明经过优化刀圈轧制性能得到了提高;(3)无论是纵向还是横向,从刀圈表面向内芯都是硬度下降的趋势,说明刀圈表面硬度较高,对提高刀圈的耐磨性能具有积极意义。经过以上分析和验证可以看出,这里提出的基于家族遗传算法的滚刀刀圈轧制优化方法可以有效提高刀圈性能,为轧制生产提供了参考。
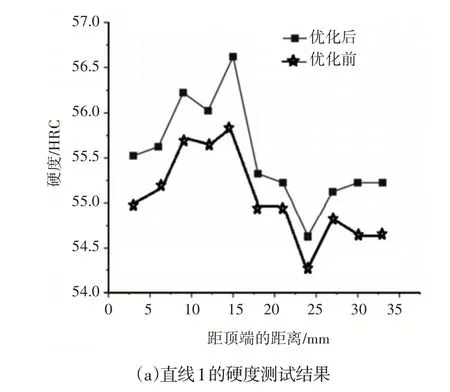
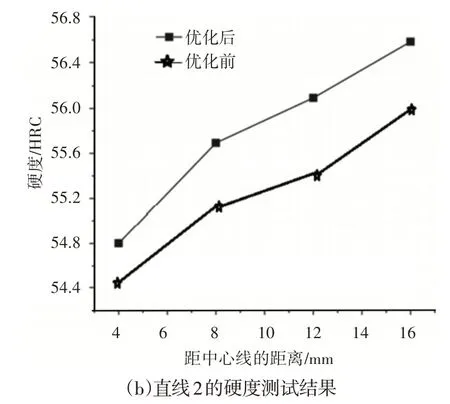
图9 硬度检测结果Fig.9 Hardness Test Result
6 结论
研究了滚刀刀圈轧制优化问题,建立了优化目标函数,使用家族遗传算法进行刀圈轧制工艺优化,经验证得出以下结论:
(1)家族遗传算法中融入了多家族并行遗传和家族间交叉方法,有效提高了家族遗传算法的搜索效率和搜索结果;
(2)经过轧制工艺优化,滚刀刀圈外观检查合格,硬度整体得到了提升。
