磁网络电机模型下电机−齿轮传动特性研究
2023-03-19陈毅韩旭朋刘焕学张全逾
陈毅,韩旭朋,刘焕学,张全逾
(1.河北石油职业技术大学汽车工程系,河北 承德 067000;2.西安交通大学机械工程学院,陕西 西安 710049)
1 引言
行星齿轮电机传动系统由于其高可靠性、高功率、低成本等诸多优点,在机械传动领域具有广泛的应用。磁网络电机模型(Permeance Network Model,简称PNM)的优势在于它可以在计算精度和效率之间实现良好的平衡,能够模拟物理场分布,在研究齿轮和电机的动态性能方面具有较好的应用价值[1−2]。
目前在齿轮和电机的动态性能研究领域的大部分研究集中电机动力学建模方面[3−4],电机建模最常用的方法是集总参数模型和有限元模型。然而,传统的集总参数模型未考虑机器内部的空间和非线性影响[5],而有限元模型在考虑空间谐波和非线性影响时需要大量的计算时间。文献[6]应用PNM方法,通过结合有限元法的磁导值来模拟感应电机的动态性能。文献[7]提出了PNM电机耦合模型,该模型可同时计算径向和切向运动的偏心力,以进行机械振动稳定性和非线性分析。文献[8]运用牛顿动力学理论建立二级齿轮传动平移−扭转动力学模型,讨论中间轴连接刚度的改变对系统动态特性的影响。文献[9]研究各种不同工况下行星轮系的非线性动态特性,提升了轮系动力学特性分析效率。文献[10]对齿轮箱行星轮系统采用集中参数法建立行星轮系扭转动力学模型,讨论了时变啮合刚度和相位差对行星轮系固有特性和稳态响应特性的影响。文献[11]考虑箱体、行星架的结构柔性后,建立风电齿轮箱耦合动力学模型,并分析了其动态响应。文献[12]推导了任意空间运动状态下中心构件和行星轮运动方程,建立了行星齿轮传动系统耦合动力学模型。文献[13]在考虑齿轮副间时变接触力和齿轮柔性的基础上,建立了系统刚柔耦合仿真模型。
本研究在前人研究的基础上提出电机−齿轮耦合系统的动力学模型,该模型在非线性磁网络模型(PNM)的基础上考虑了行星齿轮系统的横向扭转特性,应用该模型可与电机模型相结合,从而进行机电耦合动力学分析,通过仿真模拟了感应电机的动力性能,研究分析对比分析了PNM电机模型机电系统的响应与动态电机模型机电系统的响应,同时分析了磁饱和效应对机电耦合系统动力学的影响。
2 磁网络电机模型
PNM方法是将电磁系统分解成磁通管,如图1所示。以磁通量和磁通势(MMF)为变量,每根磁通管有着磁导的特征,所有磁导连接形成一个磁网络模型,出现在磁等效电路中的单元可以分为两组:有源(MMF)和无源(磁导),如图2所示。这里用磁导表示磁阻Rm的倒数,定义如下:

图1 磁通管的定义Fig.1 Definition of Fluxtube

图2 磁等效电路的几何定义Fig.2 Geometric Definition of Magnetic Equivalent Circuit
式中:∧、μ、A(x)和l—磁导、渗透率、横截面积和长度。磁通势(MMF)可以通过将每相的电流乘以定子槽中的匝数或转子回路电流来得到,转子回路电流可以表示为在磁轭或齿中。在计算磁导和磁通势(MMF)后,磁通管上的磁标量势u可由下列方程求得[14]:
式中:(u1−u2)—任意两点1和2之间的磁标量势;φ12—从点1到点2的磁通量;∧12—两点之间的磁导。
鼠笼式异步电动机(SCIM)定子和转子的磁导率以及模型中使用的几何参数,如图3所示。定子中的主磁通路径一般由定子磁轭∧sb、定子轮齿∧st和定子齿尖对齿尖∧stst磁导元件表示,图中的定子磁轭∧sb和定子轮齿∧st中的黑点分别代表定子轭Msb和定子齿Mst的节点势能,转子磁导和节点势能以类似的方式表示。

图3 定子和转子磁导几何模型Fig.3 Geometric Model of Stator and Rotor Permeance
气隙磁导是特定定子−转子之间的磁导,它取决于轮齿之间的重叠面积。对于具有Ns个定子齿和Nr个转子齿的电机系统,总共有Ns×Nr个气隙磁导。气隙磁导与转子位置的关系,如图4所示。PNM 模型考虑了定子、转子和气隙磁导,可以根据参考文献[15]中给出的方法进行计算。磁网络和电网络之间的类比关系可以通过方程(2)来建立,磁标量势、磁通量和磁导分别等效于电路的电压、电流和电导。定子节点方程可以表示为:
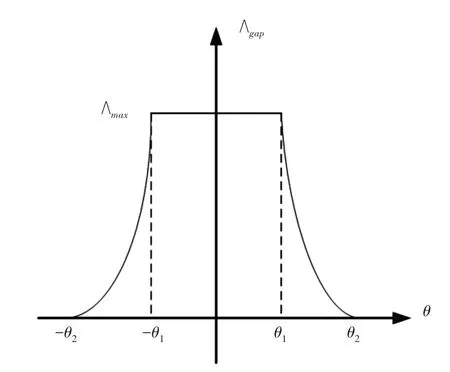
图4 气隙磁导与转子位置θ的关系Fig.4 The Relationship Between Air Gap Permeance and Rotor Position θ
转子节点方程可以类似定子节点方程得到,磁链、电压、定子和转子回路电流之间关系的方程可以写成:
式中:Vqd0—定子电压;R—转子电阻矩阵;λ—定子和转子磁链矩阵;I—电流,机电耦合扭矩τe如式(6)所示:
式中:T—电机的极数。
饱和度会影响感应电机的瞬态扭矩、电流和稳定时间。钢结构的非线性磁导μFe可以通过磁场强度H函数来获得,如式(7)所示:
式中:H=ΔM/l,ΔM—钢结构两端的磁势;l—钢结构的长度。
3 行星齿轮系统和感应电机模型
在电机−齿轮系统中,外部载荷施加在行星齿轮系统的行星架上,动力通过轴系从电机传递到行星齿轮系统的太阳轮,如图5所示。将轴简化为质点,不考虑考虑轴或电机转子的轴承,仅考虑轴的扭转刚度。所有齿轮均为无误差的正齿轮,行星齿轮均匀分布在太阳齿轮周围,太阳齿轮与轴或电机转子之间没有轴错位。由于电机的转速因整个系统的内部和外部激励而变化,在机电耦合模拟中必须考虑齿轮系统的瞬时转速。因此,在行星齿轮系统的动力学模型中,将每个齿轮和齿轮架的旋转和平移作为广义坐标。行星齿轮系统的结构,如图6所示。

图5 机电系统结构图Fig.5 Structure Diagram of Electromechanical System

图6 直齿行星齿轮系统的横向扭转动力学模型Fig.6 The Torsion Dynamics Model of Spur Planetary Gear System
太阳齿轮和齿圈的角位移θi(i=s,r)为移动坐标系OiXiYi中测量的相对值,坐标系OiXiYi固定在齿轮架上并且与齿轮架一起旋转。载角位移θc是静态坐标系OcXcYc下测得的绝对值,行星齿轮角位移θpi(i=1,2,3)是在移动坐标系Onξnηn中测量的相对值,坐标系οnξnηn固定在齿轮架上并随齿轮架移动。因此,动态行星齿轮模型中存在三个坐标系。Ts和Tc分别表示作用在太阳和行星架上的扭矩,Tr表示齿轮箱壳体作用在齿圈上的扭矩。
啮合变形独立于参考系,因此,在运动坐标系OiXiYi或οnξnηn中可以得到啮合齿轮副和轴承的变形和坐标关系。从图7中可知,可以求出齿轮和轴承的接触变形,εj(j=spi,rpi,cri,cti)代表第i个行星齿轮相对于太阳齿轮或齿圈的变形,以及第i个行星齿轮轴承相对于齿轮架的径向或切向压缩变形。太阳行星和环形行星齿轮啮合变形方程如下:


图7 行星齿轮系统的啮合变形Fig.7 Meshing Deformation of Planetary Gear System
式中:uj=rbj·θj(j=s,p1,p2,p3,r)表示太阳轮、行星轮和齿圈的旋转角,xj,yj(j=s,r)表示太阳轮、行星轮和齿圈的位移,ξj(j=1,2,3),ηj(j=1,2,3)表示第j个行星齿轮在ξ和η坐标上的位移,其余部件的接触变形可以通过类似的方式获得。
齿轮啮合的总势能由赫兹能、弯曲能、剪切能和轴向压缩能组成,啮合刚度随轮齿接触位置的变化而变化,考虑行星齿轮的啮合相位,计算太阳−行星齿轮啮合刚度,如图8所示。这三条线代表三个太阳−行星齿轮副的啮合刚度。电机的等效电路示意图,如图9所示。Lm—励磁电感;Lσs,L'σr—定子和转子漏感;Rs,R'r—定子和转子电阻,所有的定子和转子量都是在四阶d−q参考系中获得,方程中所有的参数都为常数,如下方程式所示:

图8 太阳−行星齿轮副的啮合刚度Fig.8 The Meshing Stiffness of the Sun−Planetary Gear Pair

图9 电机的等效电路示意图Fig.9 Schematic Diagram of the Equivalent Circuit of the Motor
4 机电耦合效应的动态特性分析
在仿真模型中,机电系统空载起动,在正常负载运行期间,电压会出现不同程度的不对称下降。机电系统的主要参数,如表1~表3所示。有意增加齿轮系统的轴承刚度,使其具有较大的刚度性能,在满足精度损失的条件下减小其对齿轮系统力动力性能的影响。机电模型的结构,如图10所示。

图10 机电模型结构示意图Fig.10 Schematic Diagram of the Electromechanical Model Structure

表1 磁网络(PNM)电机模型数据Tab.1 Magnetic Network(PNM)Motor Model Data

表2 动态电机系统数据Tab.2 Dynamic Motor System Data

表3 行星齿轮系统数据Tab.3 Planetary Gear System Data
利用电机机械系统和轴的微分方程,建立了与行星齿轮模型S函数相联系的PNM电机模型的Matlab/Simulink自定义函数,如式(13)、式(14)所示:
式中:J—转子的转动惯量;θmotor—电机转角;Tshaft—传输轴的扭矩;km,cm—轴的扭转刚度和阻尼。
TCB—电磁转矩计算模块,MMS—机电系统;PGS—行星齿轮轴系。可以看出,PNM电机模型和PGS具有相同的转角/转速,且都承受来自行星齿轮系统的扭矩。通过扭矩和角度/速度这两个部分的相互作用实现耦合,PNM 电机模型被简化为动态电机模型,通过Simulink非线性求解器ode23tb对整个系统进行求解。两种模型在正常载荷下太阳−行星齿轮啮合力的频谱,如图11所示。可以看出基于PNM电机的机电系统的太阳−行星齿轮啮合力的频谱比动态电机模型的具有更多的峰值。除了从1×fm到5×fm的两个模型中啮合频率fm的调制频率外,频率fT1和fT2均由PNM电机的系统的转矩频率引起的,其他频率峰值是转矩频率与啮合频率的调制频率。
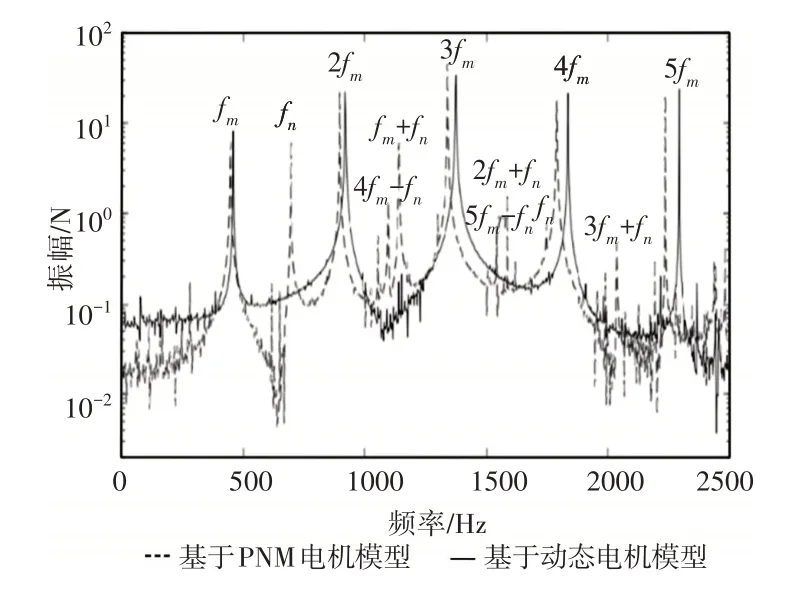
图11 太阳行星齿轮副的啮合力频率Fig.11 The Meshing Force Frequency of the Sun Planetary Gear Pair
电机系统频谱对比图,如图12所示。空载时,电机模型的电磁转矩集中在零频率,它是一条不受啮合频率影响的平滑曲线,图12(a)所示。
当施加负载时,非零频率处的振幅增加,与调制啮合频率相关的峰值可以从电磁转矩和转子速度谱看出。然而,电流显示的频率对称在啮合频率周围,即kfm±f(1其中,k=1,2,3…,功率频率f1=60Hz)与扭矩或转子速度不同。对于空载状态下的PNM电机模型系统,其转矩主频率大约为720Hz,转速主频率大约为1800Hz。同时,PNM的电流具有更多的谐波频率。
由于施加了外部载荷,扭矩频率的振幅增加,且峰值频率随着转速的降低而向左移动。当系统加载时,次谐波转矩或电流频率随着总频谱振幅的增加而衰减,并且调制啮合频率仅出现在转速频谱中,如图12(c)所示。

图12 电机系统频谱对比图Fig.12 Spectrum Comparison Diagram of Motor System
根据所提出的模型,可以看出机电耦合系统的动态啮合力不会明显影响电机的电磁转矩或电流,但会影响系统的转速,这与[17−18]的实验结果一致。
为了进一步研究磁饱和对机电耦合系统动力学的影响,将饱和状态下PNM电机的电磁转矩、电流和转速等情况,与磁饱和减弱或忽略时的情况进行比较(通过增加硅钢片的拐点磁通密度值),如图13所示。
从图13(a)、图13(b)可以看出,当饱和效应减弱时,机电转矩和电流仅具有主频,然而,当考虑饱和效应时,会出现额外的谐波分量。这些谐波分量由转子旋转频率frotor和极数T决定,可通过以下公式计算:
当饱和PNM电机负载时,总转矩频率值增加,如图13(a)所示。除了式(15)中k=2和k=5时的主频外,扭矩的谐波频率振幅逐渐衰减,且由于转速的降低,峰值频率向左移动。电流频率情况与扭矩频率比较类似,如图13(b)所示。如图13(c)所示,转速频谱与电磁转矩具有相同的频率峰值。脉冲转矩引起的速度波动是由电流谐波引起的,且它们之间相互作用。当PNM电机的饱和效应减弱时,机电系统电磁转矩的次谐波频率消失。

图13 系统频谱对比图Fig.13 System Spectrum Comparison Diagram
无论负载如何,设饱和PNM电机系统下的电流频谱主要集中在工频f1,记为主槽谐波频率,其余集中在工频和旋转频率的调制频率,记为饱和相关频率,机电耦合系统的电流频率可以通过式来计算:
主槽谐波频率:
饱和相关频率:
其中:R—转子序号;s—转子滑移系数。当忽略饱和时,磁饱和效应引起的电流谐波频率只剩下750Hz、870Hz、1570Hz、1690Hz等主槽频率。
磁饱和效应对机电耦合系统动态特性的影响,如图14、图15所示。从图14可以看出,当忽略饱和效应时,机电耦合系统的动态啮合力频谱没有显著变化。从图15(a)、图15(b)可以看出,转矩和电流频谱与图13中PNM电机模型预测的趋势比较类似。
如图15(c)所示,对于空载的两个系统,转速通常受到转矩的谐波频率的影响,当两种PNM电机系统被加载时,调制的啮合频率和扭矩频率都会显示转速频谱上。在图15(a)中,尽管转矩频谱中存在由饱和效应引起的次谐波频率,但是通过对比图14、图15(a)以及图15(c),当其负载时,啮合力或转速频谱不会受到显著影响。不同轴扭转刚度对太阳行星齿轮啮合力的均方根(RMS),如图15(d)所示。

图14 太阳行星齿轮副的啮合力频率Fig.14 The Meshing Force Frequency of the Sun Planetary Gear Pair


图15 机电耦合系统动态特性Fig.15 Dynamic Characteristics of Electromechanical Coupling System
在轴刚度较低的情况下,均方根值有一个峰值,这意味着轴刚度会导致系统严重的振动,增加轴刚度会对动态啮合力产生不同的影响,因此可以选择特定的轴刚度来优化机电耦合系统的动力性能。
5 结论
(1)在非线性磁网络模型(PNM)的基础上结合了行星齿轮系统的横向扭转特性,研究分析了电机−齿轮系统机电耦合模型的动态特性,在负载和空载状态下,分别对比分析了PNM电机模型机电系统的响应与动态电机模型机电系统的响应。
(2)研究了磁饱和效应对机电耦合系统动力学的影响。在忽略饱和效应时,机电耦合系统的动态啮合力频谱没有显著变化,转矩频谱中存在由饱和效应引起的次谐波频率,但负载时,啮合力和转速频谱不会受到显著影响。同时分析了轴刚度对动态啮合力的影响,对于优化电机−齿轮机电耦合动态特性具有重要参考价值。
