基于气温变化的简易融雪模型研究

古力米热·哈那提， 姜 波， 苏里坦， 张 音,3， 胡可可,3

（1.新疆水利水电科学研究院水资源研究所，新疆 乌鲁木齐 830049；2.中国科学院新疆生态与地理研究所荒漠与绿洲生态国家重点实验室，新疆 乌鲁木齐 830011；3.中国科学院大学，北京 100049）

全球气候变化与水资源问题是各国政府部门和学术界共同关注的焦点，也是西北干旱区实现跨越式发展的重要瓶颈之一。新疆水资源的形成和水循环过程在西北干旱区独具特色，高山拦截空中水汽形成降水，发育了众多河流。高山带的负温条件，使降水可能以降雨或降雪的形式出现，降雪中的一部分暂时或长期积储于山区，发育了大量冰川，这些高山能够提供比较丰富而稳定的径流［1］。积雪是一种重要的淡水资源，据不完全统计，尽管地球表面以雪的形式形成的降水量约占到5%，但在新疆天山冬季寒冷漫长，积雪丰富，降雪所占比例远远大于该值，甚至接近降水量的一半。天山是一个高海拔的山脉，这些山脉代表了新疆径流形成的主要地区。春季的快速变暖导致中低海拔地区和山前平原的积雪迅速融化，从而引起融雪洪水，扰乱或破坏交通、畜牧业、农业设施和人民的生命财产［2-3］。近几十年来，伊犁河谷发生了严重的春季融雪型洪水灾害［4-5］。因此，了解积雪与融雪规律，对该地区水资源评价与调控以及融雪洪水的防治具有重要意义。目前，对天山地区积雪的研究主要集中在流域尺度的积雪覆盖区遥感［6-9］，扩展产品的应用与评价［10］，反演方法的改进，径流序列的模拟［11-12］，融雪径流模型（Snow runoff model，SRM）的应用［13］，以及SRM参数的修改［14］。

融雪模型一般可分为度日模型和能量平衡模型，度日模型是典型的统计模型，在冰雪融雪研究中得到了广泛的应用［15］。典型的度日模型包括水文模型［15］和SRM 模型［16-17］，但度日模型也有其局限性。当这些模型用于不同的流域时，特定流域的模型参数需要校准。然而，人类不易到达的山区往往测站稀少甚至没有测站，导致高寒山区的气温、降水、积雪、融雪等观测数据难以获取。因此，模型中度日因子的经验和半经验参数难以获得，所得结果的可靠性也会受到影响。本研究针对以上不足，在天山西段开展了积雪、融雪以及相关气象要素的实验研究，旨在摸清融雪量与气温之间的定量关系，进而构建基于气温的简易融雪模型，揭示山区融雪变化规律以及对气温的响应机理，为流域融雪型洪水的模拟预报提供简便的算法。

1 研究区概况

研究区位于中国新疆天山北坡，流域面积约为26 km2，即在天山积雪与雪崩研究站西边的野外实验流域，流域海拔范围由1100～3100 m 之间，地势南高北低，垂直地带性明显。流域内5个不同海拔带安装了5个气象站以及降雪融雪仪器设备，最高气象站海拔高度为2120 m，出山口水文站的海拔高度约为1175 m（图1）。该地区日夜温差大，年平均气温为8.7 ℃，降雪主要发生在11月至次年3月之间。通过观测发现，流域内多年平均降水量约为550 mm，多年平均风速为1.5 m·s-1，多年平均辐射为4800 MJ·m-2·a-1左右，具有明显的半干旱区山区水文特征。

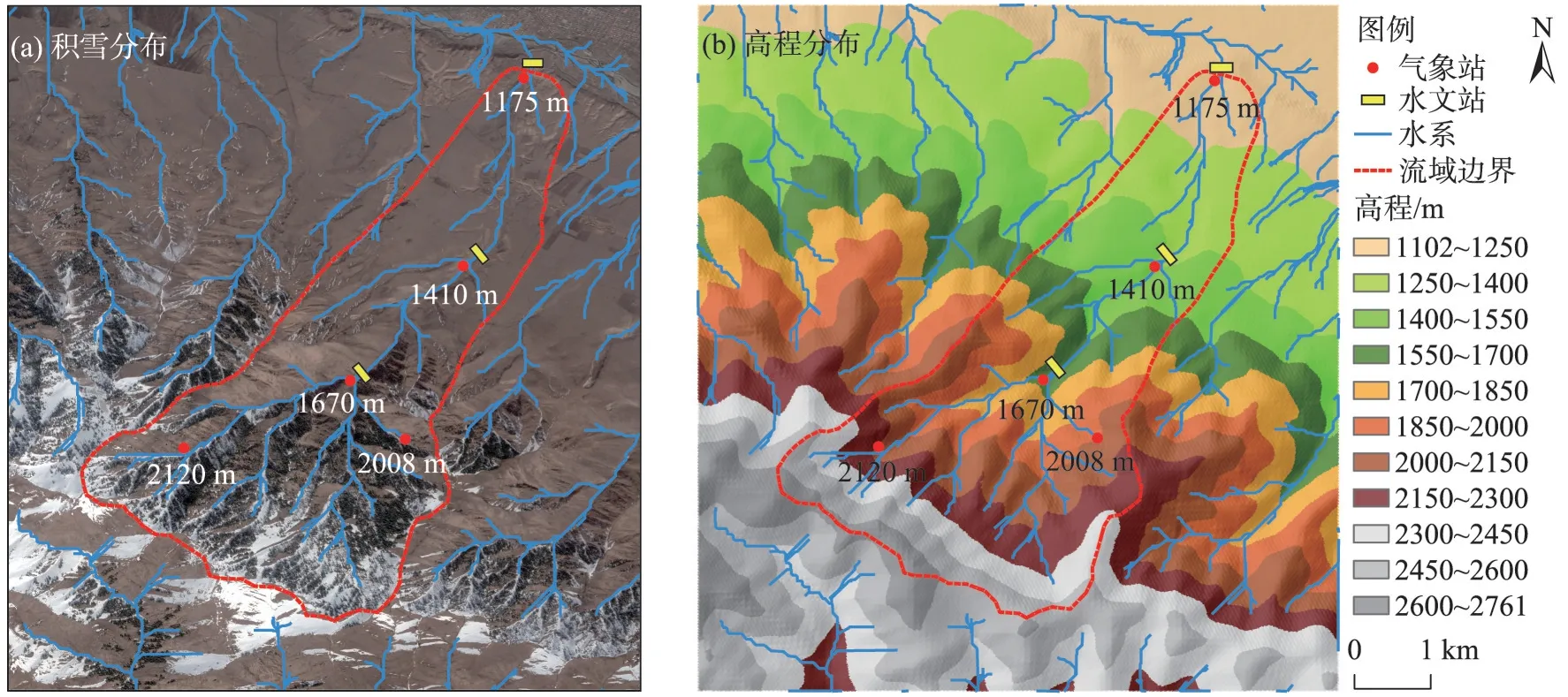
图1 阿热都拜小流域测站及水系分布Fig.1 Experimental station and river system distribution map of Araltobe Basin

2 数据与方法

2.1 数据获取

气象数据采用CAMBELL-CR1000 型采集器自动采集，测定要素包括气温、湿度、大气压、降雨量、风速、风向；融雪量采用Sommer 公司研发的SSG 型雪水当量仪测量，测量原理：SSG型雪水当量仪通过压力传感器测定不同时刻积雪的重量变化，融化的雪水通过设备上的无数小孔排出；降雪量采用T-200B 型称重式雨雪量计来测定，该设备测定累积降雪量，而不同时刻降雪量可通过相减获取；雪面升华量首先采用涡度仪测定潜热，然后用公式间接计算而得；雪面温度采用Apogee公司的SI-111型红外温度传感器测定；地表温度采用HydraProbe 型探头测定，土壤水分通过Hydra 的水分传感器探头获取，该探头集成到CAMBELL-CR1000 型采集器。为了使融雪数据具有普遍性和代表性，选取在2016 年9月1日至2021年8月31日期间（完整的5个水文年）的数据作为分析数据。

2.2 研究方法

本研究基于收集的相关数据，划分了融雪不同阶段，采用Origin 软件绘制了融雪变化曲线，分析研究区融雪变化基本规律。采用最小二乘法对长时间序列气温与对应的融雪量数据进行线性拟合，构建起简易的单因素融雪模型，划分率定期和验证期，并对结果进行评价和分析。

3 结果与分析

3.1 融雪对温度的响应规律

新疆山区降水资源是绿洲水资源的主要来源，其中高山冰雪融化是常年河流的造血器，因此，融雪径流的研究逐渐成为干旱区水文过程研究的主线。图2 为融雪速率与环境温度之间的相关性，环境温度数据（大气温度、雪面温度和地表温度）和融雪速率数据（mm·d-1）均为日平均值。由图可见，融雪速率的变化趋势与环境温度的波动同步共振，即随着环境温度的降低或升高，融雪速率也降低或升高。当气温升高到一定值时，由于积雪完全融化，融雪出现间断性现象，因此，建模时只考虑入冬至春融期间的有效融雪量。从图2 不难发现，年内不同时期甚至在冬季都有融雪发生，可见，在天山山区融雪的临界温度并不是0 ℃，而是-7 ℃左右，实验数据显示当气温低于-7 ℃时，融雪处于停止状态，而本研究中雪面升华（蒸发）的临界温度为-12 ℃，低于融雪的临界温度，这也体现了干旱环境下的山区融雪特征。

在此（图2）过程中，雪面温度的变化很大程度上依赖于大气温度的变化，积雪吸收太阳辐射得以雪层温度升高，积雪发生消融现象，可知，气温和太阳辐射是积雪产生融化的主要驱动因素，通过大量实验数据发现，气温对积雪消融的贡献大于辐射。由于积雪是地表与外界的隔离层，地表温度对气温的响应并不明显，从而融雪受地表温度的影响很小。由图可见，雪面温度和大气温度的波动趋势呈现出同步共振，考虑到气温具有易于获取的优势，因此选取气温作为影响融雪量的主要因素。

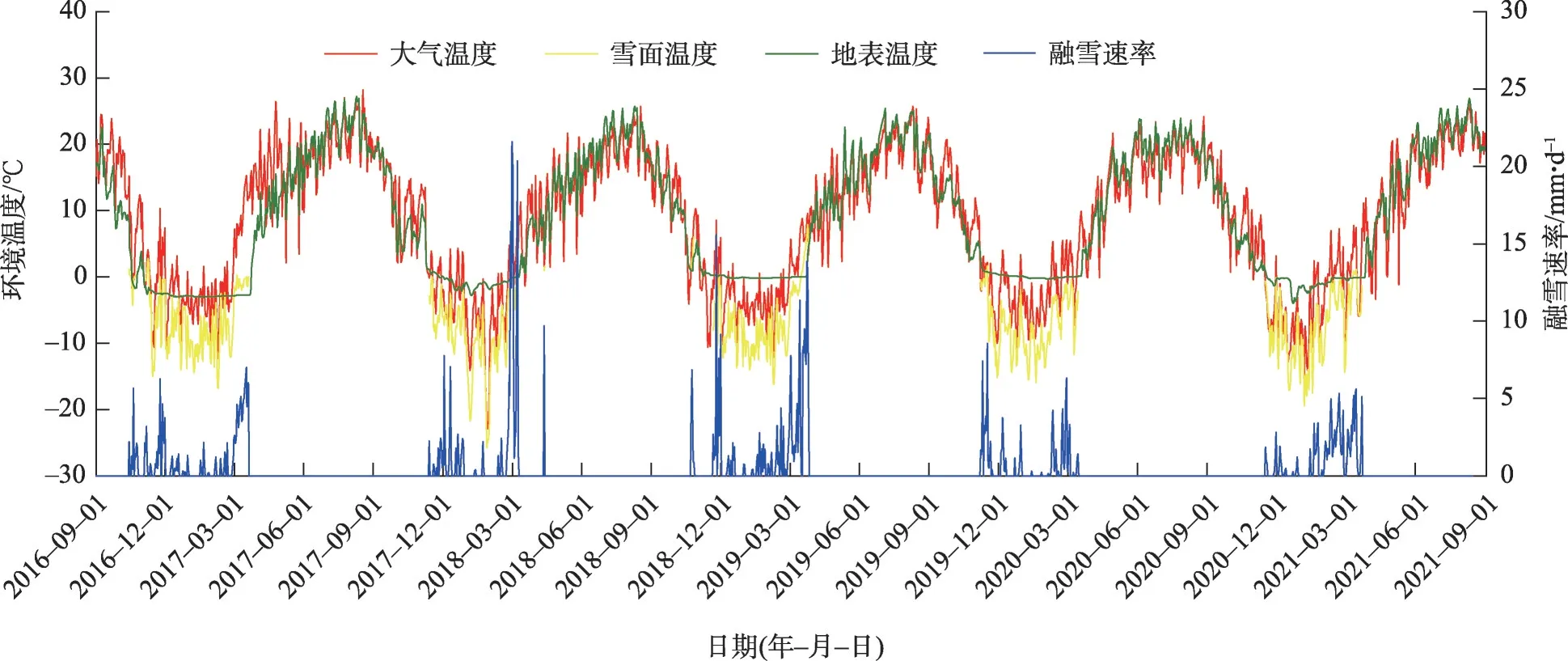
图2 融雪量与环境温度的关系Fig.2 Relationship between snow melting amount and ambient temperature

3.2 雪水当量日变化规律

图3 为2016—2020 年天山阿热都拜小流域积雪消融变化趋势线。实验观测数据显示，不同水文年降雪量占降水量的比重有所不同，累积降雪过程随着降雪逐步增长，增长速率与降雪量和气温直接相关，而融雪过程主要受气温的影响。实验区多年平均降水量约为570 mm，其中冬季降雪量为200 mm，约占多年平均降水量的35%，因此，冬季的降雪量对干旱区水资源的贡献率大于其他季节，而在海拔较高的山区更为明显。以1175 m 高程的出山口水文站数据为例，融雪过程分3个阶段，即完全消融阶段-非完全消融阶段-完全消融阶段，其中完全消融阶段的特征是气温对融雪量的贡献较大，致使累积融雪量等于累积降雪量，属于非稳定积雪期；而非完全消融阶段的特征是气温较低，使得气温不足于完全消融积雪，呈现出累积融雪量小于累积降雪量，属于稳定积雪期。3 月初随着温度的骤然回升，山区融雪量急剧增加直至消融殆尽（图3）。

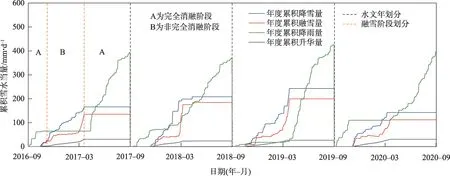
图3 积雪消融变化规律Fig.3 Variation of snow melting

3.3 基于气温变化的融雪模型

本文主要研究融雪量与气温之间的相互作用过程，通过日累积融雪量与日均气温之间的内在关系，建立基于气温变化的融雪模型。由于完全融雪期属于非稳定融雪期，气温对融雪的贡献有盈余，导致模型计算的融雪量偏高于实际融雪量，因此，建模时，融雪模型务必建立在非完全融雪阶段，而建好的模型完全适用于整个融雪阶段，但是适用在完全融雪阶段是有条件的，只要地表有积雪时，模型是可直接使用，而且其模拟结果是可靠的（4 个完整水文年的日融雪数据具有普遍性）。

3.3.1 融雪模型的构建事实上，通过大量野外观测数据发现，融雪量与气温之间存在显著的线性关系（数据分析的相关性可达90%），其余不确定性因素包括太阳净辐射、覆被指数等因素，这些因素对融雪的贡献率较小，因此舍去。

本研究选取积雪消融过程的非完全消融阶段作为建模的切入点，以气温为自变量，以融雪量为因变量构建简易的单因素融雪模型为y=ax+b，其中y为融雪量（mm），x为气温（℃），a、b分别为模型斜率和截距。通过最小二乘法对长时间序列气温与对应的融雪量数据进行线性拟合，得出如下融雪模型：

式中：SM为融雪量（mm）；Ta为气温（℃）。

考虑到融雪临界温度（Tr），将式（1）进一步改进为:

3.3.2 融雪模型的率定利用公式（2）得出天山典型流域率定期（2016—2020 年）的融雪量模拟结果（图4）。由于不同年份气温的变化趋势不同，形成的融雪量值也不同。由图可以看出，在率定期，相比图4b、4d，图4a、4c 年份的融雪量偏大，这与当年的气温较高和降雪量较大密切相关。模型模拟的波动趋势与实测值基本一致，但在融雪量的部分极值点存在比较明显的偏差。

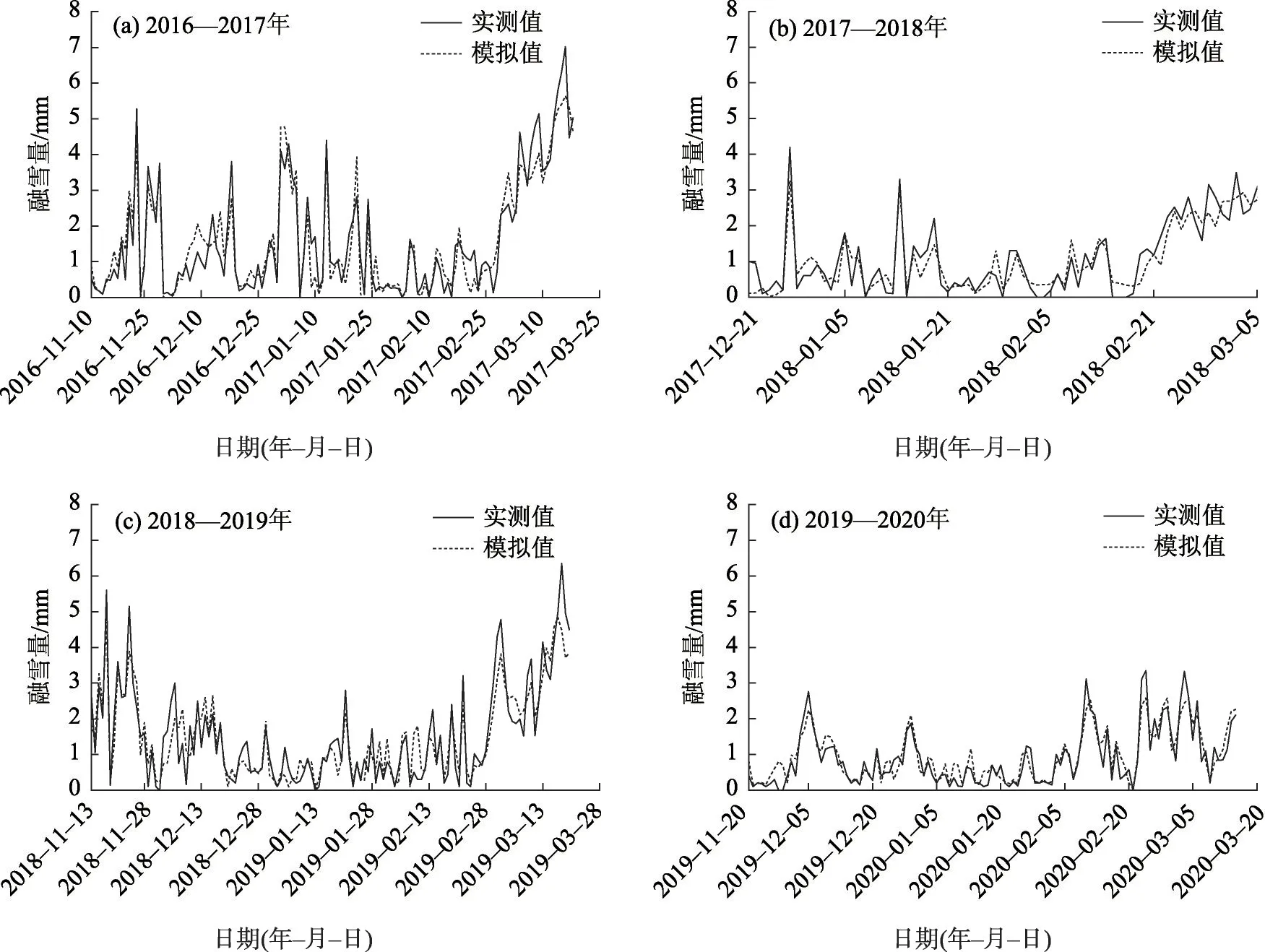
图4 率定期研究区不同年度积雪期融雪量模拟值与实测值对比Fig.4 Comparison of simulated and measured snowmelt values in different years during calibration at study area

3.3.3 融雪模型的验证图5 为研究区2020—2021年冬季融雪量模拟结果（验证期）。相比率定期，模型在验证期的模拟值与观测值存在一定的偏差，模型低估了融雪量的峰值，这除了与模型的不确定性因素（辐射、风速等）有关，还与观测设备的硬件称重和软件换算误差有关。对于单因素（气温）的线性模型而言，模型的模拟结果是令人满意的，可用简单的气温数据能获取近似的融雪量模拟结果，模型适用于长时间序列融雪过程模拟。

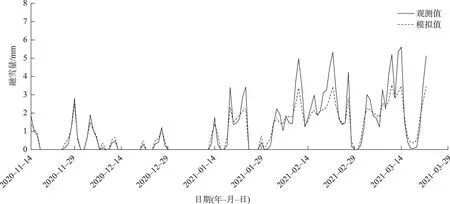
图5 2020—2021年冬季的融雪量模拟结果（验证期）Fig.5 Simulation results of snowmelt in winter during 2020—2021(in the validation periods)

3.3.4 模型的精度分析图6a 和6b 分别给出了率定期（2016—2020 年）和验证期研究区融雪量观测值与模拟值的相关性对比结果，由图6可见，率定期与验证期模型的相关性均较高，R2都达到了0.8 以上，但是模型低估了模拟值，相比率定期，验证期的模拟值偏低且偏离1:1 线幅度大，进一步分析验证期数据走势发现，当融雪量小于3 mm 时，模拟值很接近观测值（绿色线，接近y=x线），而当融雪量大于等于3 mm 时，模拟值偏小于观测值（绿色线，接近y=0.6x线），说明模型更适用于低融雪量的情景。总之，对于单因素输入而言，模型得到了满意的验证，模拟效率较高（R2>0.8），且为分布式水文模型提供简便有效的融雪子模块。

从图6 可见，相比观测值，模型模拟值偏低，其主要原因是在观测的融雪量中含有升华量，而在模型中未考虑积雪升华量因素，因此模型会低估融雪速率。

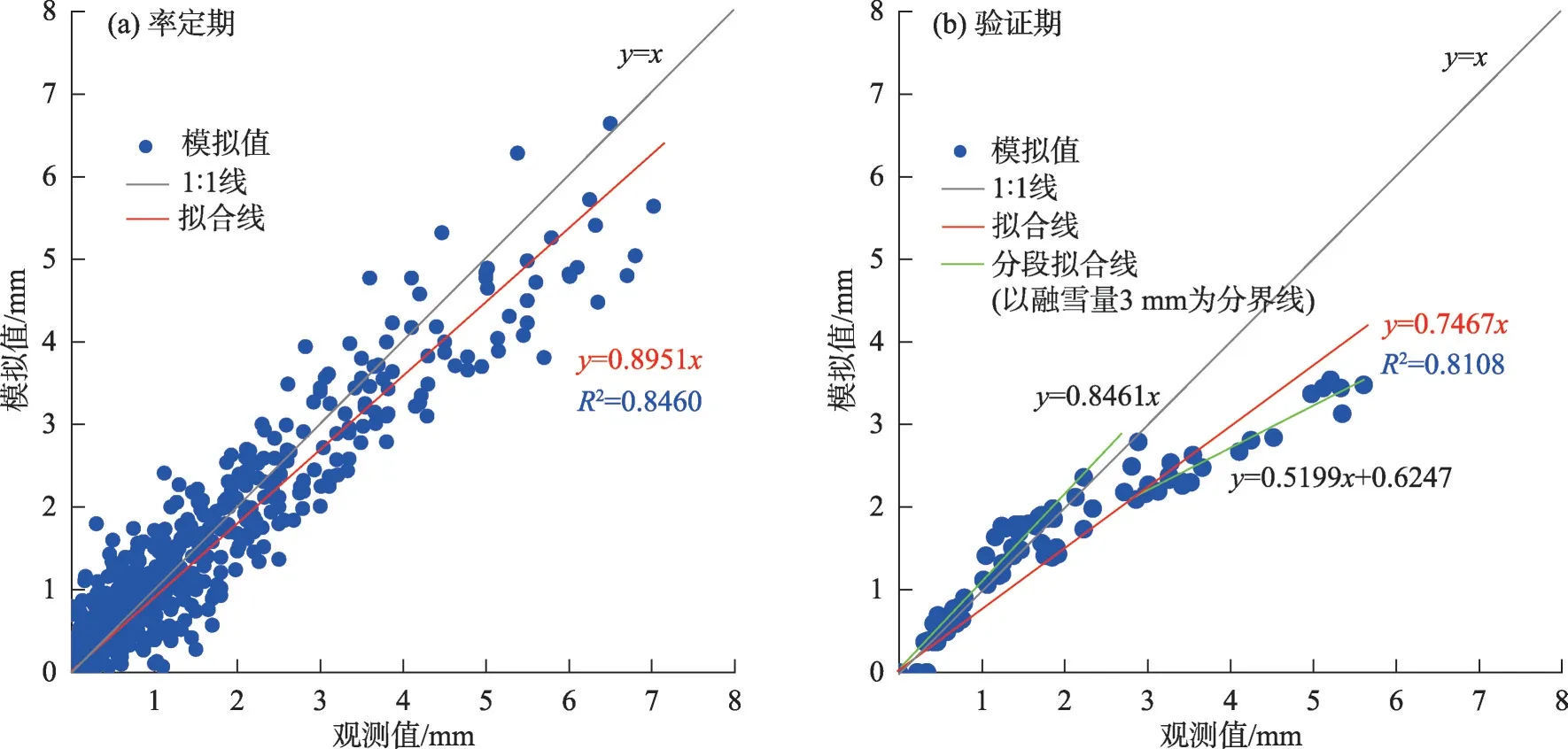
图6 融雪量观测值与模拟值相关性的散点图Fig.6 Scatter diagram of correlation between observed value and simulated value of snowmelt

3.3.5 模型的评价标准为了验证模型的有效性，采用了5 种不同的标准来评价模拟模型的性能，包括偏差（Bias）、平均绝对误差（MAE）、均方根误差（RMSE）、纳什效率系数（NSE）和决定系数（R2）。这些值表示为：

式中：z*(hi)为模拟值；z(hi)为观测值；z*(hi)ave和z(hi)ave分别为模拟值和观测值的平均值；N为数据量。在试验模型中，采用Bias、MAE、RMSE 和NSE 对模拟值与观测值的一致性进行统计分析，R2反映了拟合优度，理想条件下观测融雪量与模拟融雪量的最佳拟合时，Bias=MAE=RMSE=0，NSE=R2=1［18］。

表1是用融雪模型在率定期与验证期的观测值与模拟值的相关性评价结果。从表可见，率定期和验证期的观测值与模拟值的相关性参数总体表现好，基本上所有的Bias、MAE 和RMSE 值都低于0.5，在可接受的范围内［19］，尤其是率定期的Bias 值均低于0.1，而验证期的值超过-0.2，总体保持较低水平；融雪量观测值与模拟值的NSE 和R2均大于0.8；率定期与验证期的R2分别为0.903、0.865、0.862、0.873和0.811，说明该模型的模拟值与观测值具有良好的一致性。

表1 融雪量观测值与模拟值的相关性评价Tab.1 Correlation evaluation between simulated and measured snowmelt values

总结以上结果可知，在积雪消融第二阶段（非完全消融），大气温度对融雪量的贡献率最大（R2大于0.8），其次是太阳辐射、下垫面条件等其他因素，至于融雪量与多因素（气温、太阳辐射、下垫面条件等）之间的非线性函数关系是下一步工作重点，不作为本文的研究内容，本文专注于融雪量对气温的响应过程与规律。

4 结论

本文以伊犁站所属野外研究站监测的气象数据为自变量，以融雪量为因变量，研究基于气温变化的融雪模型，揭示了多年融雪变化规律及其对气温的响应过程，得出结论如下：

（1）通过大量观测发现，在一定的低温范围内，冬季仍有融雪发生，可见，在天山山区本项目研究流域融雪的日平均临界温度并不是0 ℃，而是-7 ℃左右，实验数据显示，当日平均气温低于-7 ℃时，融雪处于暂停状态，而本文中雪面升华（蒸发）的日平均气温临界值为-12 ℃，远低于融雪的日平均气温临界值，这也体现了干旱环境下的山区融雪特征。

（2）在雪水当量方面，融雪过程分3 个阶段，即完全消融阶段-非完全消融阶段-完全消融阶段，其中完全消融阶段的特征是气温对融雪量的贡献较大，致使累积融雪量等于累积降雪量，属于非稳定积雪期；而非完全消融阶段的特征是由于气温较低使得累积融雪量小于累积降雪量，属于稳定积雪期。

（3）基于气温构建了单因素融雪模型，为了保证模型的完整性，建模时只考虑了入冬至春融区间的有效融雪量（非完全消融阶段），而率定后的模型可适用于地表积雪的所有状态，只要地表有积雪时，模型可直接使用，而且其模拟结果是可靠的（验证期R2>0.8）。

（4）在模型的评价方面，模型在率定期和验证期的相关性参数总体表现好，Bias、MAE 和RMSE 值都低于0.5，尤其是率定期的Bias 值低于0.1，而验证期的Bias值在-0.2左右，总体保持较低水平；融雪量实测值与模拟值的NSE 和R2均大于0.8；率定期与验 证 期 的R2分 别 为0.903、0.865、0.862、0.873 和0.811，说明该模型的模拟值与观测值具有良好的一致性，其优点是通过易获取的气象数据就可以估算流域融雪量，为干旱区积雪消融计算提供了较为简便的算法，也为分布式水文模型提供简化有效的融雪子模块，研究成果同时为流域融雪型洪水的模拟预报提供技术支撑。