FBMC/OQAM 系统中改进的峰均比抑制方法

李磊，薛伦生，*，陈西宏，邹兵

(1.空军工程大学防空反导学院，西安 710051；2.中国人民解放军93145部队，南京 210000)

偏移正交幅度调制的滤波器组多载波(filter bank multi-carrier with offset quadrature amplitude modulation，FBMC/OQAM)是应用已久的正交频分复用（orthogonal frequencydivision multiplexing，OFDM）传输方案的一种新的替代方案[1-2]。与OFDM 相比，FBMC/OQAM 采用的原型滤波器时频聚焦特性较好，且系统具有更高的频谱效率、更好的频谱抑制能力，增强了对时间和频率失准的鲁棒性[3]。其优良的特性引起了许多学者的研究，包括原型滤波器的设计[4-6]、频域均衡[7-9]、信道估计[10-12]、峰值平均功率比（峰均比）（peak-to-average power ratio，PAPR）抑制[13-15]、时间同步[16-17]等。

然而，FBMC/OQAM 放松正交条件仅在实数域中保持正交性[18]。因此，即使在无失真信道中，数据符号也会受到周围符号的固有干扰，这使得信道状态信息获取和多天线部署等信号处理任务更具挑战性。为确保系统在接收端可以完整恢复出传输信号，必须对信道状态信息进行估计。而FBMC/OQAM 中存在的固有干扰会对系统的信道估计造成严重影响。为解决这一问题，学者们提出了多种信道估计方法，主要分为基于离散导频和基于导频序列的信道估计方法。其中，经典的基于导频序列的信道估计方法有干扰近似法（interference approximation method，IAM）、成对导频法（pairs of pilots，POP）和干扰消除法（inter ference cancellation method，ICM）。ICM 方法是利用原型滤波器的固有干扰系数重新设计导频序列结构，将导频间的固有干扰相互抵消，从而减小系统固有干扰对信道估计的影响。文献[19-21]是3 种典型的ICM 方法，对导频结构进行设计，抵消导频间固有干扰，保证了信道估计精度。但这3 种方法的导频序列占用了3 个 偏 移 正 交 幅 度 调 制(offset quadrature amplitude modulation，OQAM)符号，导频开销较大，实用性较低，且没有考虑一阶邻域外的干扰对信道估计的影响。基于此，文献[22]进行改进，用辅助导频(auxiliary pilot，AP)代替传统ICM 的保护导频序列，以消除码间干扰对信道估计的影响，显著降低了FBMC/OQAM 系统的导频开销，同时增大了系统固有干扰的消除范围，使系统的信道估计精度得到效提高。

同时，FBMC/OQAM 作为多载波系统，如果多个子载波相位相同，那么在时域叠加的信号峰值幅度会过高，从而导致PAPR 较高。发送端信号在通过功率放大器时会到达非线性区域，降低放大器工作效率且导致信号失真，引起误码率的增加。因此，降低系统过高的PAPR 是非常有研究意义的[23]。

文献[22]有很好的信道估计性能，但其过高的PAPR 在实际系统中并不实用。本文在该方法基础上进行改进，把插入的导频序列与原始符号组成新的数据符号，给新的数据符号乘以不同的相位旋转因子，分别计算其PAPR，并选择PAPR 值最小的一组作为发送信号。通过仿真证明，在不影响其信道估计性能的前提下，系统过高的PAPR 得到抑制，且误码率不高。

1 FBMC/OQAM 系统特性

如图1 所示，同样作为多载波系统的FBMC/OQAM，在结构上沿用OFDM 系统的IFFT/FFT 结构，有效降低了系统复杂度[24]。不同的是，OFDM系统采用循环前缀的方法对抗载波间干扰（inter carrier inter f erence，ICI）和符号间干扰（inter symbol interference， ISI）， 然 而FBMC/OQAM 系 统 采 用OQAM 的调制方式，有效提高了频谱效率。

图1 FBMC/OQAM系统框图Fig.1 System block diagram of FBMC/OQAM

FBMC/OQAM 的连续时间基带传输信号为

式中：gm,n(t)表 示滤波器在时频坐标 (m,n)处的综合基函数，且

其中：M为子载波的数量(M为偶数)；am,n为 第m个子载波上传输的第n个 符号；g(t)表示脉冲成型滤波器函数； τ0为FBMC/OQAM 相邻符号的实部与虚部的时间间隔；v0为子载波间隔，且v0=1/T0=1/(2τ0)，T0表 示一个符号周期； ϕm,n为相位因子，表达式为

当基函数gm,n(t)满足实数域正交的条件时，接收端才可以准确地恢复出发送端的信号，即

式 中， 〈x,y〉 表 示x和y的 内 积； ℜ{•}表 示 取 实 操 作，表示复共轭； δ为冲激函数，其定义为

在理想无失真信道条件下，即接收信号r(t)=s(t)，OQAM/OFDM 系统在接收端时频格点 (p,q)处的接收复数符号为

式（7）中的第2 项为系统的固有虚部干扰，假设信道理想无失真，接收端通过对取实部操作就可以恢复出传输符号，即

在实际的多径信道中，ICI 和ISI 的存在会影响传输符号的恢复过程，因此，信道估计是系统重构数据符号必不可少的环节。

信号经过脉冲传递函数为h(t)、带有高斯噪声η(t)的信道后，接收信号表示为

式中： ∆为信道的最大时延； η(t)为均值为0、方差为∆的高斯白噪声。

假设原型滤波器在符号间隔内变化缓慢，符号时间间隔远大于信道脉冲响应长度，即g(t−τ−nτ0)≈g(t−nτ0)，此时式（9）可写为

则对时频格点 (p,q)处的接收信号进行解调可得到

式中：Ip,q表示系统的固有干扰。

从式(11)中可以得到，即使不考虑信号经过信道时噪声的干扰，由于FBMC/OQAM 系统固有的虚部干扰Ip,q的存在，仍然会对信道估计性能造成影响。因此，要得到良好的信道估计性能，就要消除FBMC/OQAM 系统中的虚部干扰。

2 改进的基于相位旋转的干扰消除法

2.1 常见的ICM 方法

FBMC/OQAM 系统采用干扰权重系数呈对称分布的原型滤波器[25]，可以根据此特点及对导频结构的合理设计来消除邻域内的固有干扰。ICM就是基于此原理对导频结构重新设计。

最简单的结构ICM-1 如图2 所示，其在偶数或奇数子载波上放置非零导频，在其他子载波上则均放置零，以消除ICI 的影响；将非零导频相邻的左右2 列数据符号设为零，以消除ISI 的影响。

图2 ICM-1导频序列结构Fig.2 Frame configuration for ICM-1

图3 的导频结构ICM-2 利用干扰权重系数在频率方向上的对称性来消除ICI 的影响，同时保留了两旁的零保护序列来消除ISI 的影响，且在所有子载波上均放置了非零导频。

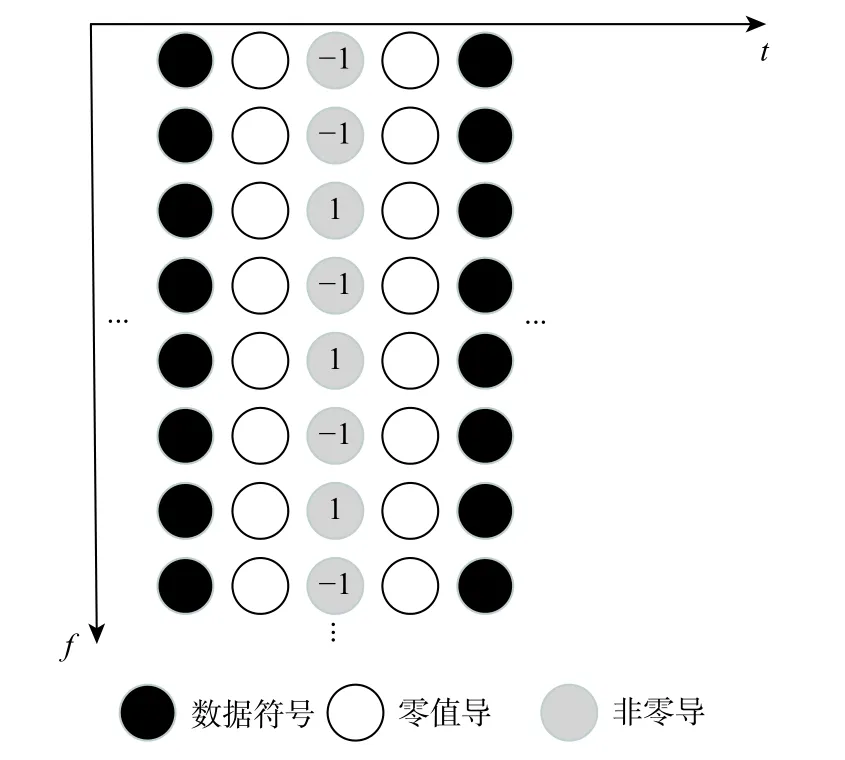
图3 ICM-2导频序列结构Fig.3 Frame configuration for ICM-2

图4 的导频结构ICM-3 则是同时利用干扰权重系数在时间和频率方向上的对称性来消除ICI和ISI 的影响，所有导频序列均放置非零导频，避免了插值过程带来的误差影响。

图4 ICM-3导频序列结构Fig.4 Frame configuration for ICM-3

上述3 种方法导频序列均占用了3 个OQAM信号，导频开销较大，使得其实用性较低。同时，其均假设虚部干扰只在一阶邻域内，忽略了一阶邻域外的虚部干扰对信道估计性能的影响。

考虑一阶邻域外的干扰时，式（11）应写为

式中：

式中： Ω1,1表示导频的一阶邻域。

针对上述3 种ICM 导频开销过大的问题，文献[22]的ICM-NEW 去除了非零导频左右2 列的零值保护序列，同时在非零导频左右均放置一个AP，以消除邻域内符号ISI 对导频的影响。结构如图5所示。

图5 ICM-NEW导频序列结构Fig.5 Frame configuration for ICM-NEW

2.2 ICM-P

上述几种ICM 的信道估计性能与误码率性能都比较优越，尤其是ICM-NEW。但是作为实际应用，由于加入了导频序列，系统PAPR 较高，经过发射端的功率放大器会引起失真，影响放大器的性能。本文主要针对ICM-NEW 的PAPR 较高的缺点进行改进。

根据采样定理对FBMC/OQAM 系统进行采样，则离散时间发送信号为

式中：Lg为原型滤波器的长度。

ICM 方法都是在时频格点图中插入导频符号进行信道估计，令第n个 符号第m个子载波上的数据符号为， 导频符号为，则本文提出的基于相位旋转的干扰消除法（interference cancel lation method w ith phase rotation，ICM-P）步骤如下：

1）将导频符号插入到数据符号中组成新的符号，即

2）定义相位旋转因子P u:

3）将新的符号S与 相位旋转因子P u进行点乘，得到不同的输出序列S u，即

4）将得到的序列S u分别进行IFFT 得到时域序列s u。

5）分别计算每个时域序列的PAPR，并选择PAPR 值最小的作为发送端数据。

记使传输数据的PAPR 值最小的相位旋转因子索引为v，则相位序列P v应同传输符号一起发送给接收端，以便接收端进行信道估计与传输数据的恢复。

2.3 CCDF 曲线

FBMC/OQAM 符号是在一个符号周期之内传输一帧符号，其PAPR 的定义为

式中：E{•}为信号的均值。

多载波系统在发送端由多个复数信号叠加，并经过多个子载波进行传输，如果子载波的相位相同，则多个信号的叠加会增加信号的瞬时峰值幅度，从而使PAPR 增加。通常计算PAPR值大于某一门限值的概率，得到互补累积分布函数(complementary cumulative distribution function，CCDF)。CCDF是衡量系统峰均比高低的标准，即

式中：Pr为 某一事件的概率； γ为门限值。

3 仿真分析

仿真选用IEEE 802.22 标准信道中典型的多径信道A 信道，各项参数如表1 所示。主要仿真ICM-P在不同相位序列组数条件下及不同方法在不同子载波条件下的PAPR 抑制性能、误码率性能、信道估计性能。

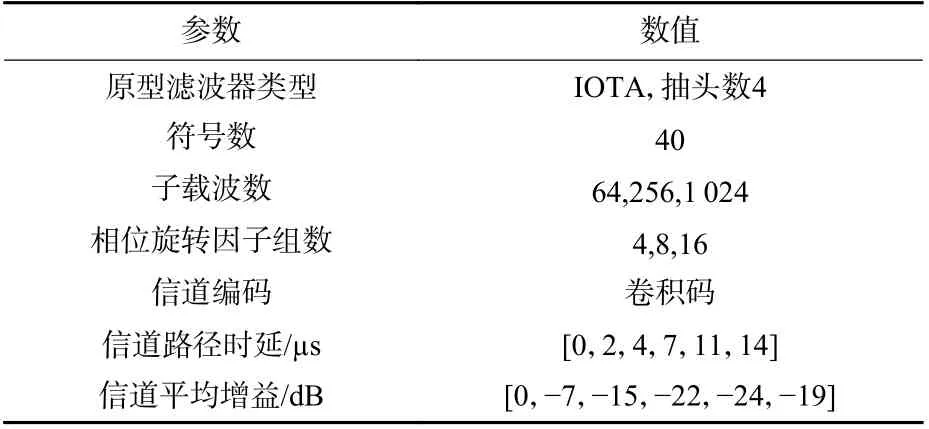
表1 参数设置Table 1 Fundamental param eters of simu lations

3.1 PAPR 抑制性能

图6 给出了ICM-P 与ICM-NEW、原始系统在载波数M为256 时的CCDF 曲线。可以看出，ICMNEW 对导频序列重新设计后，其PAPR 较原始系统要高，这更容易引起发送端信号的失真。ICM-P 与原始系统及ICM-NEW 相比，PAPR抑制性能明显较好，且随着相位序列组数U的增加，PAPR 进一步减小。当U=16、CCDF=10−3时，系统PAPR 较原始系统下降约6.8 dB。

图6 不同方法的CCDF曲线Fig.6 CCDF of different methods

图7 给出了ICM-P 与原始系统的CCDF 曲线随子载波变化的曲线，此时ICM-P 的相位序列组数U 为16。可以得出，随着子载波数目M的增加，系统的PAPR 值会有所增加，但较原始系统相比，ICM-P的PAPR 抑制性能依旧明显。当子载波M=1 024、CCDF=10−3时，ICM-P 的PAPR 比原始信号降低约6.6 dB。

图7 不同子载波的CCDF曲线Fig.7 CCDF of different subcarriers

3.2 误码率性能

ICM-P 与ICM-NEW 的误码率BER 性能曲线如图8 所示。对于固定的子载波数目，随着信噪比SNR 不断增加，系统的误码率不断降低。当相位序列组数U=8且 子载波数目M相同时，ICM-P 的误码率性能较ICM-NEW 相比有所提升，且随着子载波数目M的增加，系统的误码率越来越低，即误码率性能越来越好。

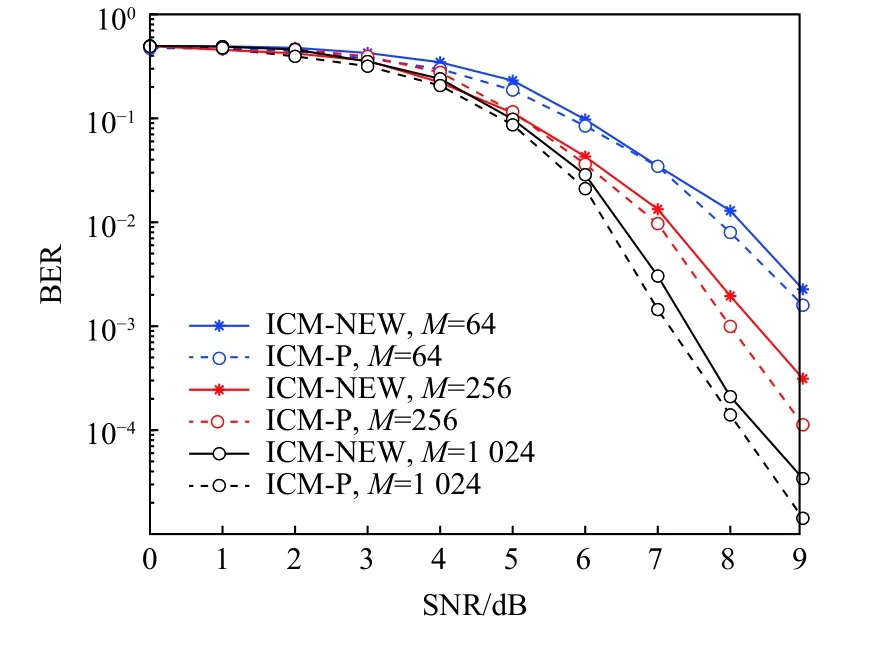
图8 不同子载波的误码率曲线Fig.8 Bit error rate of different subcarriers

当子载波数目M=256时，不同的相位序列组数的误码率性能曲线如图9 所示。可以看出，随着相位序列组数U的逐渐增多，系统的误码率逐渐增高，即误码率性能逐渐下降。

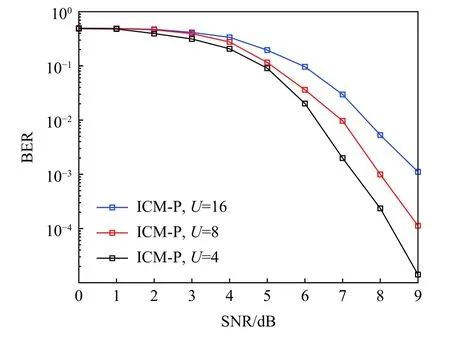
图9 不同相位组数的误码率曲线Fig.9 Bit error rate of different phase groups

3.3 NM SE 性能

标准均方差（normalized meansquared error，NMSE）是衡量系统信道估计性能的指标。图10 为子载波数为256 时几种方法的NMSE 性能曲线。可以看出，ICM-P 与ICM-NEW 的NMSE 性能较为接近。当信噪比较小时，文献[26]的信道估计性能最好，但随着信噪比的逐渐增大，ICM-P 的信道估计性能与文献[26]所提ICM 方法也逐渐接近。

图10 不同方法的NMSE曲线Fig.10 NMSE of different methods

3.4 复杂度分析

为对信道进行有效的估计，ICM-NEW 方法在原始系统中加入了非零导频与辅助导频，占用了一定的频带空间，且较原始系统相比复杂度有一定的增加。ICM-P 在ICM-NEW 的基础上增加了相位旋转因子及PAPR 的运算，运算量有所增加。但是，ICM-P 有效降低了系统的PAPR，避免了信号经过功率放大器时的失真现象。ICM-P 牺牲了一定的复杂度，使系统的可靠度大大提升，且有效降低了系统的硬件成本。

4 结 论

ICM-P 对ICM-NEW 的PAPR 过高的缺点进行改进，通过传输数据与不同的相位序列相乘得到不同的序列，选择时域PAPR 值最小的序列用于传输。通过仿真可以得出：

1）ICM-NEW 会增加系统的PAPR，而ICM-P有很好的PAPR 抑制性能。且系统的PAPR 抑制性能随着相位序列组数U的增加越来越好，随着子载波数目M的减少越来越好。当M=256、U=16、CCDF=1 0−3时，ICM-P 的PAPR 较原始 系 统 下 降 约6.8 dB；M=1 024、U=16、 CCDF=1 0−3时，ICM-P 的PAPR 比原始信号降低约6.6 dB。

2）相同信噪比与子载波条件下，ICM-P 的误码率性能较ICM-NEW 有所提升。且子载波数目增加，误码率性能增加，相位组数增加，误码率性能下降。

3）在固定信噪比与子载波数的条件下，ICM-P与ICM-NEW 的NMSE 性能接近。

4）ICM-P 牺牲了一定的复杂度使系统的可靠度大大提升，且有效降低了系统的硬件成本。