基于Transformer 模型的滚动轴承剩余使用寿命预测方法

周哲韬，刘路，宋晓，陈凯

(1.北京航空航天大学自动化科学与电气工程学院，北京 100191；2.北京航空航天大学网络空间安全学院，北京 100191；3.南京航空航天大学机电学院，南京 210016)

滚动轴承被称为“工业的关节”，是旋转机械设备的关键零件，广泛应用于各个工业领域[1]。如在航空航天领域，轴承是航空发动机承力传动系统[2]及航天器控制力矩陀螺[3]等设备的重要组成部分，其性能与质量直接影响了航空航天设备的安全性与可靠性。轴承若发生故障，轻则将导致设备故障、经济损失，重则将引发安全事故、人员伤亡。因此，准确、及时地预测轴承的剩余使用寿命（remaining useful life，RUL）对工业生产安全而言具有重大研究意义。

随着传感器、存储、网络传输等新技术的快速发展，轴承运行过程产生了大量的监测数据，利用这些数据来挖掘轴承退化信息，实现精确的RUL预测，是当前的研究热点[4]。基于数据驱动的轴承剩余使用寿命预测主要有2 个步骤[5]：①从原始信号中提取具有趋势性的特征，来表征轴承性能退化的过程；②构建预测模型，使用传统机器学习或深度学习的方法，利用其拟合能力建立特征与剩余寿命间的关系。

特征提取是进行轴承RUL 预测的前提，目的是提取出符合轴承退化趋势的特征用于表征退化过程。传统的特征提取方法是计算原始振动信号的统计特征，如均方根、峭度、峰峰值等，以及构造一些新的统计特征，如王冰等[6]采用的基于多尺度形态分解谱熵，李洪儒等[7]采用的二元多尺度熵。近年来，深度学习凭借其卓越的非线性函数自动映射能力在滚动轴承特征提取领域得到广泛应用。如Ren 等[8]提出使用时间卷积网络从更大的振动信号感受野中提取特征；杨宇等[9]提出一种改进的深度信念网络，直接以滚动轴承原始振动信号作为网络输入，经过逐层抽象表示，挖掘出原始振动信号深层本质特征。

但是文献[6-9]中时间卷积网络、深度信念网络等深度学习方法往往需要大量标签数据进行有监督微调，标签数据的缺乏与难以获取严重制约了深度学习特征提取，而传统统计特征在单调性与趋势性上相比于轴承退化趋势往往不尽人意。针对这些问题，鉴于轴承退化是一个累积退化过程，本文对传统特征采用累积变换的方式优化其单调性与趋势性，使其在表征轴承退化过程中有更好的表现。

在对原始振动信号进行特征提取的基础上，需要构建预测模型来对轴承RUL 进行预测。轴承RUL预测本质上是时间序列预测问题，而循环神经网络（recurrent neural network，RNN）在时间序列处理方面具有明显的优越性，从而被广泛应用于轴承RUL预测领域。Guo 等[10]采用RNN 提取表征轴承退化的特征量进行轴承剩余寿命预测，并用指数模型验证预测效果，取得了很高的预测精度。Chen 等[11]提取频谱的5 个带通能量值作为特征，提出了一种具有注意力机制的编解码框架的RNN 用于轴承寿命预测。康守强等[12]利用稀疏自动编码器进行特征提取，采用双向长短期记忆神经网络进行轴承剩余寿命预测。

在处理时间序列时，RNN 下一时刻的输出取决于先前时刻的输出及当前时刻的状态，这在本质上是一种串行的运行方式，会严重制约模型运行速度[13]。同时，RNN 的每一次递归都伴随着信息的损耗，导致其在输入长序列的条件下捕捉依赖关系的能力迅速衰减，即出现记忆力退化现象。针对以上问题，本文将采用基于Transformer 的预测模型来进行轴承RUL 预测。Transformer 模型的核心原理是自注意力机制(self-attention)，其在具体实现上主要以矩阵乘法为基础，从而可以捕捉输入序列中任意向量之间的依赖关系，不受向量之间距离的影响。同时self-attention 的这种运行原理实现了并行计算，相比于只能串行计算的RNN 极大地提升了运行速度[14]。基于以上特性，Transformer 一经提出就引起了研究者的广泛关注，在机器翻译、阅读理解、文本摘要等多个领域展现出了优异的应用效果。本文将Transformer 模型引入到滚动轴承RUL预测领域，提出一种基于Transformer 模型的滚动轴承剩余使用寿命预测方法，属于Transformer 模型的全新应用，为其在工业领域增加了新的应用场景。

1 累积特征提取

滚动轴承常用的状态监测数据包括振动、声波和温度信号，其中振动信号得到了广泛分析，因为其提供了大量关于轴承内部异常的信息。但是滚动轴承的振动信号在采集时不可避免地会混入大量无意义的噪声信号，这对轴承RUL 的准确预测是不利的。因此，本文采用离散小波变换对振动信号进行去噪，通过小波分解、细节分量阈值处理和小波重构来剔除无意义的噪声，将去噪后的振动信号进行特征提取。

本文对去噪后的振动信号进行三角函数变换与统计特征提取。三角函数可以是单调递增或单调递减的，如反双曲正弦(asinh)和反正切(atan)函数，其能将原始数据转换为更低的尺度，所以将其作为振动信号的退化特征进行补充。三角函数变换按以下方式执行：用三角函数逐因素操作单次采样振动信号X，并进行标准差计算以提取特征。同时，选取一些滚动轴承RUL 预测常用的统计特征作为退化特征，具体信息如表1 所示。其中：xi为单次采样振动信号X中的第i次采样值。

在现实生产环境中，滚动轴承会不可避免地经历退化过程直至故障，而能够反映轴承退化趋势的特征将有助于轴承RUL 的准确预测。尽管表1 所示的特征是基于专家知识提取的，并且在一些应用中被证明是有效的，但是传统的统计特征的单调性与趋势性相比于轴承退化趋势往往不尽如人意，不能很好地表征退化趋势。针对这个问题，鉴于轴承退化是一个累积退化过程，本文采用了一种有效的特征变换方法，即将提取的特征变换为相应的累积形式。具体来说，累积变换是通过在时间序列上应用一个累积函数来进行的，在这个时间序列中，同时逐点执行累加和缩放操作，然后使用累积特征来表征退化的趋势。累积变换执行如下：

表1 特征和相应的计算公式Table 1 Feature and corresponding form ulas

式中：J为特征种类数量；N为特征值个数；fj(a)为第j种特征的第a个特征值；cjn为fj(a)在n个特性值中的累积变换结果。从式（1）中可以看出，如果存在噪声则其会随着累加操作而逐步被放大，所以累积变换算法容易受到不必要噪声的影响，因此，在变换前对特征进行平滑处理是非常必要的。本文采用Savitzky-Golay 滤波器来提高数据精度的同时不失真信号的趋势。平滑过程通过线性最小二乘法采用低次多项式拟合相邻数据点的连续子集来实现。

在累积变换之后，设计度量来评估转换后特征的质量是至关重要的。一般来说，有2 个常用的指标来评估构造的特征对RUL 预测的适用性，即单调性和趋势性。

单调性反映了特征的增减趋势，是退化特征的重要组成部分。其计算方法如下：

式中：N为特征值个数；为特征值的变化差异，在实际计算时为后一个特征值减前一个特征值；No.of＆gt;0为差异值大于0 的个数；M=1、M=0 分别为特征的高度单调趋势和不单调趋势。

趋势性是用来描述退化状态如何随运行时间变化的。换句话说，这个度量表征了一个与特征及与时间的相关性有关的函数。其计算方法如下：

式中：xn和yn分别为特征和时间的值；N为特征值个数。T的范围为[−1，1]，−1 为特征值严格递减，1 为特征值严格递增。

2 基于Transformer 的滚动轴承RUL预测模型

在基于数据驱动的滚动轴承RUL 预测的最新研究中，循环神经网络获得了广泛的应用（包括RNN，长短期记忆神经网络，门控循环单元及各类变种模型），但其串行计算方式和长序列依赖捕捉不敏感仍严重制约了模型运行速度与预测精度。因此，本文提出一种基于Transformer 结构的滚动轴承RUL 预测模型，旨在提高轴承RUL 预测的精度与速度。

Transformer 是一种基于注意力机制的神经网络，在自然语言处理等领域取得了良好的效果，但是其独特的结构限制了不能直接应用于RUL 预测领域，如轴承RUL 预测的数据与自然语言的词向量间的有效映射等问题。所以本文针对滚动轴承RUL预测场景进行了改进，结构如图1 所示，模型由4 个部分组成，分别为位置编码、编码器、解码器及全连接神经网络。

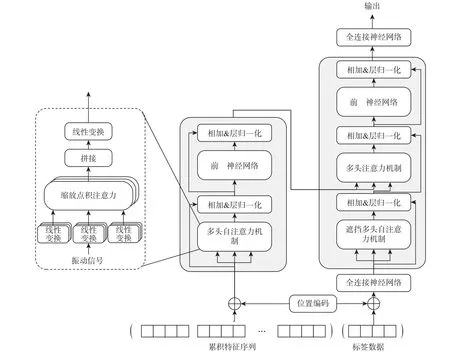
图1 基于Transformer的轴承RUL预测模型Fig.1 Bearing RUL prediction model based on Transformer

基于Transformer 的滚动轴承RUL 预测模型的核心在于其编码器与解码器结构，编码器与解码器均由6 层相同层堆叠而成，其中编码器每一层包含多头自注意力机制和前馈神经网络2 个子层，解码器每一层包含遮挡多头自注意力机制、编码-解码器多头注意力机制和前馈神经网络3 个子层。

编码器负责将输入的滚动轴承特征序列进行编码，映射为包含输入特征信息的中间向量，其核心原理为自注意力机制。自注意力机制是注意力机制的变体，减少了对外部信息的依赖，更擅长捕捉数据或特征的内部相关性，主要是通过计算特征向量间的相似度来表征相关性，以此解决长距离依赖捕捉问题。自注意力机制的目的是从输入的滚动轴承特征序列中筛选出少量重要的信息，使用权重代表信息的重要性，使得模型聚焦于更为重要的信息上。

自注意力机制采用缩放点积注意力来计算特征矩阵的注意力值，先对查询矩阵和键矩阵进行点积与SoftMax 归一化来计算权重系数，再根据权重系数对值矩阵进行加权求和，如式(4)～式(7)所示：式中：Q为查询矩阵；K为键矩阵；V为值矩阵。这3 个矩阵由输入的特征矩阵Xf分别与对应的权重矩阵W Q、W K、W V相乘得到，d为Q、K、V的维数。

自注意力机制可以让模型聚焦于输入特征的某些重要信息，但是单一的注意力机制只能在一个表现空间中学习到相关信息。为了综合输入序列包含信息的重要性，采用多头自注意力机制在不同位置共同关注来自不同表现子空间的信息。多头自注意力机制其实是多个自注意力机制的拼接，利用多个自注意力头分别学习不同表现子空间的信息，再将多个注意力值进行拼接与线性变换，得到最终的注意力值，实现对不同约束条件的建模表达，如式(8)和式(9)所示：

解码器负责将编码器输出的中间向量解码为输出序列，其核心原理为编码-解码多头注意力机制及遮挡多头自注意力机制。编码器中的多头自注意力机制注重学习输入特征序列自身向量之间的依赖关系，但为了提高滚动轴承RUL 预测的精准度，还应考虑输入特征序列与标签数据之间的依赖关系，所以在解码器中采用了编码-解码多头注意力机制。编码-解码多头注意力机制与编码器的多头自注意力机制不同，其键矩阵K与值矩阵V来自编码器的输出，包含输入序列的信息，查询矩阵Q来自遮挡多头自注意力机制模块的输出，包含标签数据的信息。

遮挡多头自注意力机制模块的输入为标签数据，其目的是利用多头自注意力机制学习标签数据之间的依赖关系，并将依赖关系输入编码-解码多头注意力机制模块，使整个基于Transformer 的滚动轴承RUL 预测模型可以综合学习输入特征向量之间的依赖关系、标签数据之间的依赖关系及二者相互的依赖关系。需要注意的是，在模型训练过程中，滚动轴承RUL 的标记数据是已知的，解码器根据并行计算特性同时完成序列每个时间步的解码。这会导致在缩放点积注意力计算时，每个时间步的计算会学习到未来的标签数据信息，这是不符合现实规律的，所以需要在解码器的多头自注意力机制中加入遮挡操作，屏蔽未来的标签数据信息。具体的操作是在计算缩放点积注意力时，引入一个下三角及对角线均为1，上三角为0 的矩阵，与QKT相乘，使得未来的序列信息置0。

为了解决网络深度增加反而影响轴承RUL 预测准确率的问题，编码器与解码器的各个子层之间均添加了残差连接操作，关注训练前后差异部分变化，提升训练效果。同时，为了加快网络收敛，提升网络泛化能力，每个子层还同时采用了层归一化操作，如下：

式中：b为网络输入参数；Sublayer 为每个子层内部的函数，本文中为各个注意力机制层处理函数和全连接前馈神经网络处理函数；LayerNorm 为层归一化处理函数。

Transformer 的一系列优点得益于其纯粹的注意力机制构造，但这使其失去了学习序列位置信息的能力。而在滚动轴承RUL 预测场景中，序列中向量的位置信息代表着时刻信息，对RUL 预测起到至关重要的作用。针对这个问题，在编码器与解码器的输入序列中加入位置编码操作，将位置信息整合到输入序列当中，如式(11)和式(12)所示：

式中：p为特征向量的位置；dmodel为特征向量的维度，每一个特征向量的位置编码都是由不同频率的余弦正弦函数组成的，波长逐渐由 2π增 长到 2 0 000π。

Transformer 模型最初是针对自然语言处理领域提出的，其输入特征与标签数据均为维度一致的词向量，相同的维度便于编码-解码多头注意力机制的直接计算。但在轴承RUL 预测场景中，输入特征为多维数据，而标签则是一维的剩余寿命，两者的维度冲突导致编码-解码多头注意力机制无法运算。针对这个问题，本文在编码器输入端直接采用累积特征序列作为输入，在解码器输入端加入一层全连接网络，将输入标签序列进行升维，在输出端同样加入一层全连接网络进行降维，解决了基于Transformer 的轴承RUL 预测模型中输入特征与标签数据维度不一致的冲突。

3 滚动轴承RUL 预测流程

基于累积特征与Transformer 的滚动轴承RUL预测方法流程如图2 所示，具体步骤如下。

图2 滚动轴承RUL预测流程Fig.2 Flow chart of RUL prediction for rolling bearings

步骤 1信号去噪。对滚动轴承原始振动信号进行离散小波变换，包括小波分解、细节系数阈值处理和小波重构，在消除异常噪声信号的同时保留有用的退化信息。

步骤 2特征提取。首先，根据已有的专家知识，在经过去噪的重构信号上计算出常用的轴承RUL预测统计特征，包括峰峰值、标准差、均方根、三角特征等；再利用Savitzky-Golay 滤波器对所有统计特征进行平滑处理，以减少提取特征的波动和进一步滤除不需要的噪声；然后，对结果平滑处理的统计特征进行累积变换，优化特征的单调性与趋势性；最后，计算所有累积特征的单调性与趋势性值，以此来筛选用于训练与测试的特征，并划分训练集与测试集。

步骤 3Transformer 模型构建。将训练集的特征进行最大、最小值归一化作为Transformer 模型的输入，将寿命比值P（剩余使用寿命与全寿命的比值）作为模型的标签数据，与轴承运行时间满足一次函数模型[15-18]。计算训练模型的均方误差(mean squared error，MSE)作 为 损 失 函 数，采 用Adam优化算法进行模型训练与优化，并采用Dropout 技术防止模型过拟合。

步骤 4测试集验证。将测试集的累积特征输入到已经训练好的Transformer 模型中，预测出特征对应的寿命比值P。由于4.1 节案例1 中PHM 2012测试集提供的是非全寿命数据（即记录滚动轴承从运行开始到某个时间点的数据），缺少退化过程末期的数据，所以需要将前半部分特征预测的寿命比值P进行拟合，以此预测滚动轴承的全寿命运行时间。由于P为寿命比值，与轴承运行时间满足一次函数模型，所以本文采用一次线性函数拟合来预测滚动轴承的RUL。

4 实验验证

4.1 案例1：PHM 2012 数据集验证

4.1.1 PHM 2012 数据集介 绍

为了验证所提出的RUL 预测方法的有效性与先进性，本文首先采用IEEE 协会在PHM 2012 数据挖掘挑战赛中提供的数据集，该数据集由PRONOSTIA 实验平台采集获得，采集装置如图3 所示。采集装置通过速度传感器和力矩传感器实现了3 种不同工况下的滚动轴承加速退化，进行了17 次轴承全寿命周期实验，利用加速度传感器采集了轴承水平方向与垂直方向共计17 组原始振动信号数据集，并将其划分为6 组训练集与11 组测试集。采集装置每隔10s 采集0.1 s 内的原始振动信号，采集频率为25.60k Hz，即每1 0 s 采集2 560 组样本数据。数据集的详细信息如表2 所示，具体实验内容参考文献[19]。根据文献[20-21]中的相关研究，水平振动信号通常比垂直振动信号给出更多的有用信息来跟踪轴承退化。因此，本文仅使用水平振动信号进行实验。

表2 PHM 2012 数据集工况信息Table 2 Operating condition inform ation of PHM 2012 dataset

图3 PRONOSTIA采集平台Fig.3 The PRONOSTIA platform

4.1.2 特征提取与筛选

在对滚动轴承的原始振动信号进行特征提取之前，本文采用离散小波变换对其进行去噪。其中小波分解采用多贝西四阶小波(db4)为母小波，分解层数为4，细节分量阈值处理中采用软阈值函数和最大、最小阈值，最后通过小波重构得到去噪后的信号。

根据第3 节的预测流程，原始振动信号去噪之后需要应用三角函数、提取统计特征和进行累积变化。如图4 所示，传统的统计特征表现出较低的单调性与趋势性，这不利于RUL 预测模型学习轴承的退化趋势，同时较高的尺度也不利于预测模型的训练过程。而结合了标准差与三角函数(提取方案见表1)的三角特征具有更高的单调性、趋势性及更低的尺度，有利于预测模型的训练过程。

图4 三角特征与传统特征对比Fig.4 Comparison of trigonometric features and classical features

如图5 所示，仍有大量数据驱动的滚动轴承RUL 预测方法采用传统的时域、频域及时频域统计特征，但是这些传统的统计特征往往无法很好地表征轴承的退化趋势，如图5(a)和图5(c)所示，仅经过平滑处理的特征单调性与趋势性各不相同，单调性较差。而从图5(b)和图5(d)不难看出，累积变换后的特征表现出了更好的单调性与趋势性，说明本文采用的累积变换对于传统的统计特征的趋势性与单调性具有很好的优化作用。

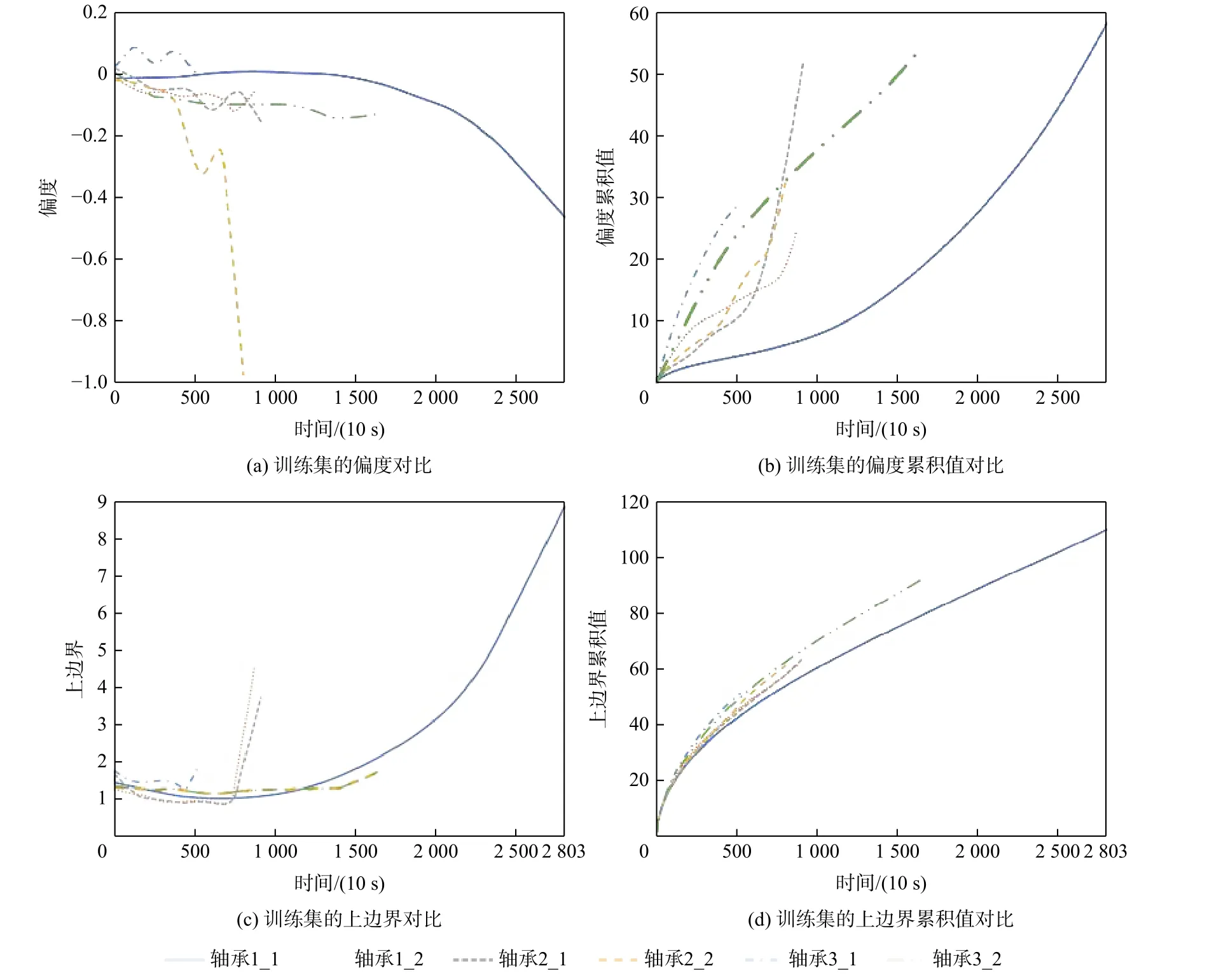
图5 累积特征与传统特征对比Fig.5 Contrasts of cumulative features and classical features

为了更好地说明累积变换的优势与必要性，本文采用式(2)和式(3)量化计算每种统计特征累积变化前后的单调性与趋势性，表3 显示了6 个训练集的统计特征累积变化前后的单调性与趋势性平均值，从表3 中可以看出，累积变化对本文选取的统计特征的单调性与趋势性具有非常明显的改进作用。由于在滚动轴承RUL 预测中，特征的单调性与趋势性越好，越能表征轴承的退化趋势，RUL预测的精度就越高，因此，本文舍弃了经过累积变换后单调性和趋势性仍然较差的平均绝对值，将剩余12 个统计特征的累积值输入Transformer 预测模型进行模型训练。

表3 累积变换前后比较Table 3 Com parison before and after cumulative transform ation

4.1.3 模型训练与预测结果分析

本文遵照PHM 2012 数据集的划分，将轴承1_1，1_2，2_1，2_2，3_1，3_2 的全寿命数据作为训练集，将剩余轴承的非全寿命数据作为测试集，具体划分信息如表4 所示。训练集经过累积变换与筛选后的12 个累积特征需要输入Transformer 预测模型进行模型训练。Transformer 预测模型是序列到序列(sequence-to-sequence)类型的模型，需要确定输入数据与标签数据的序列长度，过短的序列长度会导致Transformer 的注意力机制不容易学习到各个时间步中的依赖信息，过长的序列长度则需要巨大的计算量，降低运算速度。因此，本文选择10 个时间步的累积特征作为输入序列，10 个时间步的寿命比值P作为标签数据，寿命比值P的计算式为

表4 实验数据（PHM 2012 轴承数据集）Table 4 Experim ental data(PHM 2012 Datasets)

式中：actRUL0为轴承实际的全寿命数值，如轴承1_1 从投入使用到报废共采集了2803 组数据，其寿命数值为0～2802，则其actRUL0 为2802，由于数据采样间隔为10 s 一组，所以轴承1_1 真实的全寿命时间为28030s；actRULt则为t时刻轴承的剩余使用寿命数值。从寿命比值P的计算式不难看出，其符合一次函数关系式，所以在模型验证阶段本文也采用了拟合一次线性函数的方式来预测RUL。

为了更好地让预测模型学习到累积特征与轴承RUL 之间的映射关系，本文将输入序列的步长设置为1 个时间步，如第1 组输入为1～10 时间步的累积特征序列，第2 组输入则为2～11 时间步的累积特征序列，每一组输入序列只留取输出序列中最后一个时间步的寿命比值P作为预测结果，以此达到数据增强的效果。

本文Transformer 预测模型的编码器与解码器均由6 层相同的模块层堆叠而成，所有的多头注意力层的头数均为2，所有前馈神经网络隐藏层神经元数量为256，初始学习率设置为0.000 1 并随机初始化权重矩阵，使用均方误差（mean-square error，MSE）作为损失函数并通过Adam 优化算法进行训练，训练与测试环境中CPU 为Intel Co r e i7-10700F，GPU 为NVIDIA Ge Fo r c eRTX2060SUPER，内存为16GB，深度学习框架为Py t o r c h 1.6.0。

模型训练完毕后需要对其进行验证，与模型训练过程相同，将测试集的12 种累积特征以10 个时间步的长度输入预测模型中，预测出寿命比值P。

引言中提到Transformer 模型相比于循环神经网络具有速度上的优势，为此本文在使用累计特征的基础上，采用了长短期记忆网络[22]（long shortterm memory，LSTM）、门控循环单元[11]（gated recurrentunit，GRU）、双向长短期记忆网络[23]（bi-directional long short-term memory，BiLSTM）3 种循环神经网络作为预测模型进行对比实验，实验结果如表5 所示，其中的运行时间是根据11 个测试集中每个样本的平均时间计算的。从表5 的对比结果看出，Transformer 模型在运行速度上具有明显的优势。

表5 运行速度对比结果Table 5 Running speed comparison results

本文采用一次线性函数拟合预测的P值，得到P值的未来趋势，以此计算轴承RUL 的预测值。部分测试轴承的测试及拟合结果如图6 和图7 所示。本文采用误差El来验证预测模型的好坏：

图6 轴承1_4预测结果Fig.6 Bearing 1_4 prediction results

图7 轴承2_5预测结果Fig.7 Bearing 2_5 prediction results

式中：actRULl为第l个轴承实际的剩余使用寿命；preRULl为第l个轴承剩余使用寿命的预测结果。以轴承1_5 为例，由表4 可知，轴承1_5 的全寿命数据为24 6 3 组，非全寿命数据为2 302 组，其中预测值的拟合直线与x轴的交点（即P=0 轴承完全报废）为24 4 7 组。由于数据采样间隔为1 0 s 一组，所以act-RULl实际剩余使用寿命为（2463−2302）×10=1610s，preRULl剩余使用寿命预测值为（2447−2302）×10=1450s，则误差为（1610−1450）/1610=9.9%。

为了证明本文所提方法的有效性与必要性，本文设置了另外2 种消融实验方案来与本文所提方法进行消融实验，2 种消融实验方案详情如表6 所示。其中经典统计特征指的是将累积特征中选取的12 种特征未经累积变换的值输入预测模型中。文献[24]提出将Transformer 模型用于航天涡扇发动机的RUL 预测中，但其仅使用了Transformer 模型的编码器结构，本文采用的是完整的Transformer编码器-解码器结构，相比于单编码器结构上进行了改进，所以在消融实验方案中将单编码器结构作为对比实验条件之一。

表6 所提方法与其他2 种方案的构成Table 6 Composition of the proposed prediction method and other two schem es

为了更好地将所提方法与消融实验方案及其他先进的预测方法进行比较，需要建立一个统一的评估指标来衡量预测结果的准确性。因此，本文采用IEEE PHM 2012 挑战赛规定的平均得分s作为方法比较时的衡量标准，平均得分s的计算方法如式(15)和式(16)所示：

式中：El为第l个轴承的误差；Al为第l个轴承的得分；L为数据集的轴承总个数。

如图8 所示为误差El与得分Al之间的函数关系。从图8 中可以看出，正的误差比负的误差具有更高的得分。正的误差代表预测的RUL 小于实际的RUL，即超前预测，而负的误差代表预测的RUL 大于实际的RUL，即滞后预测。在实际生产环境中，超前预测带来的风险远远低于滞后预测，所以这种得分计算方法对滞后预测进行了惩罚，是公平且合理的。

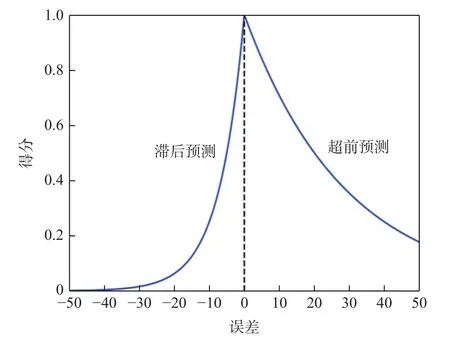
图8 得分Al与误差El的函数关系Fig.8 Function of Al and error El

同时，在表示11 个测试轴承的整体预测误差的时候，如果直接使用误差El的算数平均值，有时会导致正负误差相互抵消，出现较差的预测结果计算出较低的平均误差的情况，针对这个问题，本文采用平均绝对误差表示测试轴承的整体预测误差：

表7、表8 列出了PHM 2012 数据集中11 个轴承的数据在所提方法中的平均绝对误差与平均得分，同时也列出了与2 种消融实验方案及文献[11,25-26]方法的对比实验结果，从对比实验结果可以看出：

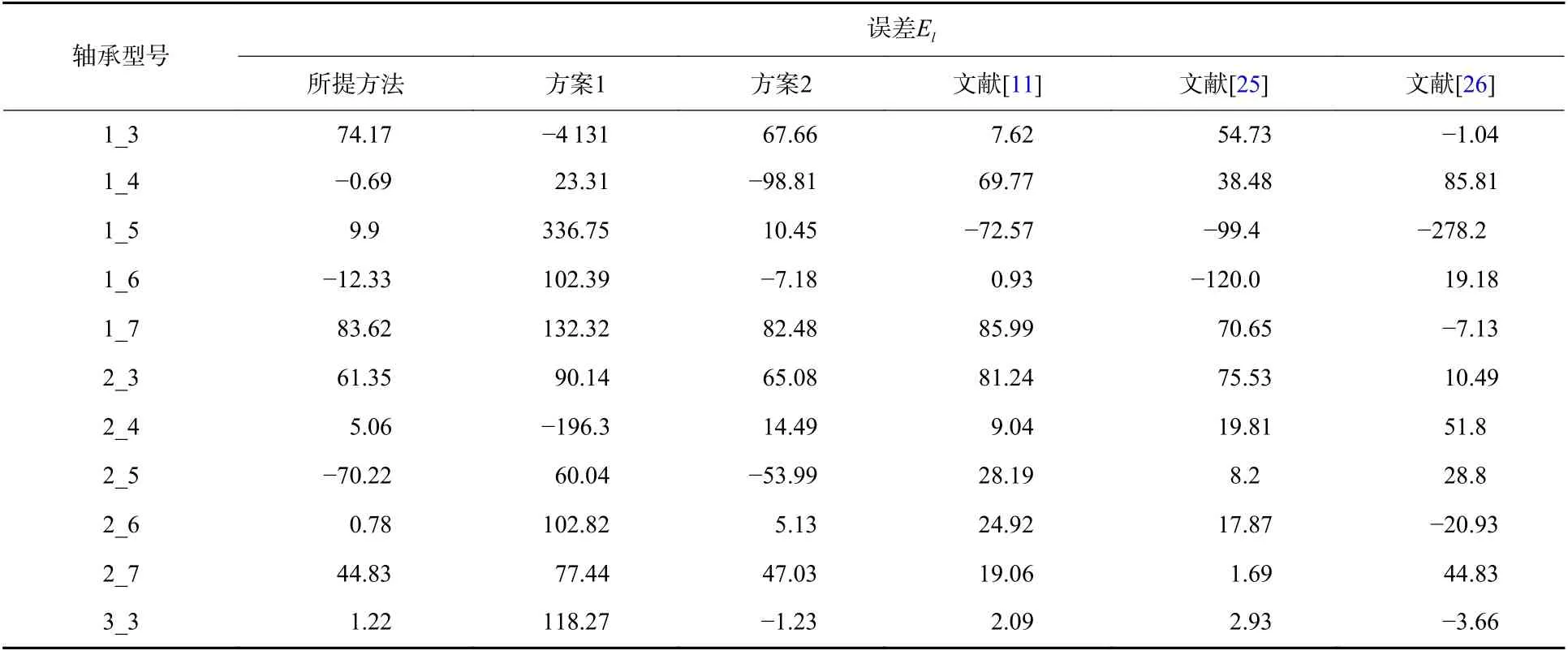
表7 所提方法和对比方法在PHM 2012 数据集RUL 预测结果Table 7 The RUL prediction results of the proposed method and comparison method in the PHM 2012 dataset

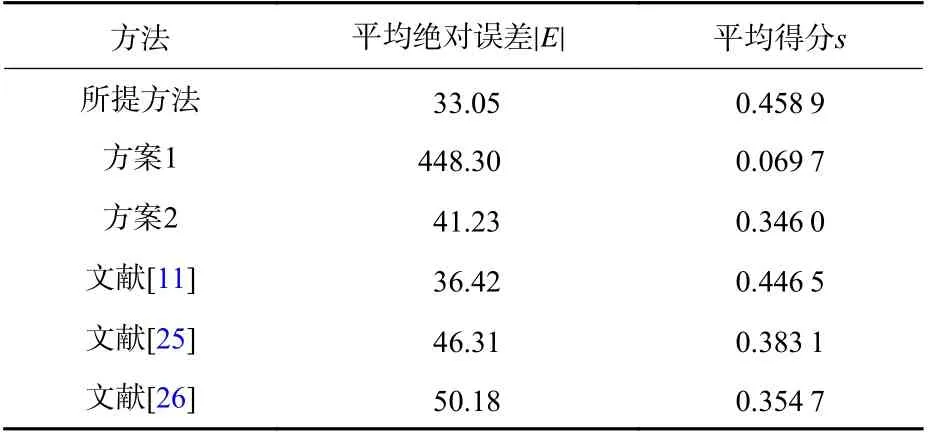
表8 表7 的预测结果比较Table 8 Com parison of predicted results in Table 7

1）方案1 同样使用编码器-解码器结构Transformer 模型作为预测模型的情况下，由于累积变换之前的传统统计特征单调性和趋势性很低，无法表征滚动轴承的退化趋势，所以表现出了极低的预测性能。而使用累积特征则大幅改善了这种情况，使得平均绝对误差降低了92.63%，平均得分提高了558.39%，可见本文所采用的累积变换对于传统统计特征的单调性与趋势性起到了极强的修正作用，对于轴承RUL 的准确预测起到了至关重要的作用。

2）方案2 在同样使用累积特征作为输入的情况下，完整编码器-解码器结构的Transformer 模型相比于单编码器结构模型的平均绝对误差降低了19.84%，平均得分提高了32.6%，这是由于单编码器结构的Transformer 模型只学习到了输入序列中各个特征向量之间的依赖关系，而解码器结构的引入可以使得Transformer 模型学习到标签数据中各个向量之间及输入特征与标签数据相互之间的依赖关系，使得RUL 的预测更为准确，由此证明了本文所提方法在轴承RUL 预测领域的优越性。

3）综合前两点方案1、方案2 消融实验的对比分析可以看出，本文所提方法的优越性是累积特征与Transformer 模型综合作用的结果，累积特征确保Transformer 模型能够挖掘出原始振动和轴承健康状况之间的潜在关系，使其能够学到绝大部分测试轴承的退化趋势，并将滞后预测（El＆lt;0）的情况控制在较低范围内。但是仍有个别测试轴承的预测误差较大，如轴承1_7，这是由于轴承1_7 的测试数据占全寿命周期数据的比重较小，少量退化前期的数据不足以让模型准确预测到退化后期的RUL。

4)同时，本文所提方法相较于文献[11,25-26]的方法平均绝对误差分别降低了9.25%、28.63%、34.14%，平均得分分别提高了2.78%、19.79%、29.38%，由此进一步证明了本文所提方法在滚动轴承RUL预测方面的有效性与优越性。

4.2 案例2：XJTU-SY 数据集验证

4.2.1 XJTU-SY 数 据 集 介 绍

为了进一步验证本文所提方法的有效性与先进性，本文还采用了XJTU-SY 数据集进行验证。XJTU-SY 数据集由西安交通大学机械工程学院雷亚国教授团队设计并采集获得[27]，其实验平台如图9 所示，该平台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成，能够在不同运行条件下对轴承进行加速退化实验，并获得完整的运行至失效数据。径向力由液压加载系统产生并施加到被测轴承的壳体上，转速由交流感应电机的速度控制器设定并保持。图10显示了正常和退化轴承的照片，可以看出，被测轴承的失效是由不同类型的故障引起的，包括内圈磨损、保持架断裂、外圈磨损、外圈断裂等。为了采集被测轴承的振动信号，2 个PCB 352C33 单向加速度传感器分别通过磁座固定于测试轴承的水平和竖直方向上。采样频率设置为25.6k Hz，每1m in记录3276 8 个数据点(即每1mi n 的采样时间为1.2 8 s)。

图9 滚动轴承实验台Fig.9 Testbed of rolling element bearings

图10 退化轴承照片Fig.10 Photographs of normal and degraded bearings

4.2.2 实验结果对比与分析

在XJTU-SY 数据集的验证过程中，本文使用了与案例1 相同的实验环境与操作流程进行训练与测试。为了验证所提方法的有效性与先进性，本文将实验结果与文献[28]的实验结果进行了比较，为了便于比较，本文采用了与该文献相同的实验方案，如表9 所示。文献[28]得到了4 种预测模型在XJTU-SY 数据集上的实验结果，分别为基于剩余自注意力机制的时间卷积网络(temporal convolutional network with residual self-attention mechanism，TCNRSA)、深度可分卷积网络(deep separable convolutional network，DSCN)、递归卷积神经网络(region w ith CNN features，RCNN)及相关向量机(relevance vector ma c h i n e，RVM)。采用均方根误差(r o o t mean square error，RMSE)与平均得分s作为实验结果对比的衡量标准，RMSE 的计算如下：

表9 实验方案Table 9 The experim ental scheme

式中：actPr为第r个测试样例的寿命比值P的实际值；prePr为第r个测试样例的寿命比值P的预测值；R为测试样例数量。

平均得分s的计算如式(14)～式(16)所示,但是由于XJTU-SY 数据集提供的均为全寿命周期数据，并未像案例1 中PHM 2012 数据集一样截断了测试集的一部分数据用于规定寿命预测时间点，所以本文在案例2 的s计算中参照文献[28]的做法，对所有测试样例均进行了平均得分s计算并取平均值。

实验的对比结果如表10 所示，从表10 中可以看出，本文所提方法预测模型相比于其他4 种模型具有更低的RMSE 及更高的平均得分，相比于TCN-RSA模型RMSE 降低了17.4%，s提高了18.6%，这进一步验证了本文所提方法的有效性与先进性。进一步对比可以发现，深度学习模型(Transformer、TCN-RSA、DSCN、RCNN)的表现均优于传统的机器学习模型(RVM)，这是由于传统机器学习模型局限于浅层学习，对滚动轴承的退化过程学习能力有限，而深度学习模型由于其突出的深层次学习能力，可以更好地挖掘轴承退化信息，建立更准确的滚动轴承RUL预测模型。而在这其中，Transformer 由于其强大的自注意力机制，能够挖掘出输入特征与轴承退化程度自身及相互之间的依赖关系，因此，其表现优于其他3 种深度学习模型。

表10 XJTU-SY 数据集RUL 预测结果与比较Table 10 RUL prognostics results and com parisons on XJTU-SY dataset

5 结 论

本文提出了一种基于累积特征与Transformer模型的滚动轴承剩余使用寿命预测方法，通过实验验证得到以下结论：

1）本文采用的累积变换对于传统统计特征的单调性与趋势性具有很强的修正作用，使得累积特征能够很好地表征轴承的退化趋势。实验证明，在同样使用Transformer 预测模型的情况下，累积特征相比于传统统计特征平均绝对误差降低了92.63%，平均得分提高了558.39%。

2）本文提出的基于编码器-解码器结构Transformer 模型的轴承RUL 预测模型，能够更好地挖掘出输入特征与轴承RUL 之间复杂映射关系，使得RUL 的预测更为准确。实验证明，在同样使用累积特征的情况下，本文的预测模型相比于单解码器结构的Transformer 预测模型平均绝对误差降低了19.84%，平均得分提高了32.6%。

3）本文所提方法能够确保预测模型挖掘出输入特征与轴承RUL 之间复杂映射关系，使其能够学到绝大部分测试轴承的退化趋势。案例1 中的PHM 2012 数据集验证实验证明，本文所提方法平均绝对误差分别降低了9.25%、28.63%、34.14%，平均得分分别提高了2.78%、19.79%、29.38%。

4）本文在案例2 中采用了XJTU-SY 数据集进行进一步的验证，实验表明，本文所提方法均方根误差降低了17.4%，平均得分提高了18.6%，由此进一步证明了本文所提方法在滚动轴承RUL 预测方面的有效性与优越性。

在后续的研究中，应该注意到滞后预测的危害，在实际生产环境中滞后预测相比于超前预测会带来更大的事故风险。本文所提方法虽然提高了整体预测精准度，但在个别轴承的工况下还存在滞后预测（如案例1 轴承2_5 的实验结果），下一步的研究重点应该是着眼于如何降低滞后预测误差或尽可能消除滞后预测。