物理习题课“立——破”思维案例分析

米海滨

(乌鲁木齐市第四十一中学，新疆 乌鲁木齐 830000)

物理习题课是物理众多课型中至关重要的一种，他直接影响到学生对所学知识的掌握程度，从而影响学生学习物理的兴趣，兴趣对学生学习物理至关重要，今天和大家交流我自己认为比较有兴趣且实用的一种习题课中的“立——破”思维.我的这种思维最早起源于下面这道题.

例1现有一个金和银组成的王冠，用排水法测出其体积为56.9cm3.若与王冠质量相同的纯金块和纯银块的体积分别为52.5cm3和96.5cm3，则王冠中银的质量和金的质量之比为多少？

该题中如果将质量相同的金全部换成银质量增大44cm3，而本题中最后的合金比纯金体积大4.4cm3，所以我们可以将纯金和纯银都按质量等分10等份，用一份纯银去替换等质量的一份纯金，体积便会增大4.4cm3，也就是说这道题只用一份纯银去替换等质量的一份纯金，即合金中有一份纯银，九份纯金，质量比为1∶9.对于密度计算，我们会特别关注密度定义质量与体积之比即单位体积的质量.但是上面这道题如果要想到上面的巧解，需要反其道而行之，想到单位质量的体积，上题中等分完每一份纯金和纯银的质量都相等，只是体积不同.这道题给了我启发，让我研究并实践了一种提高物理习题课的方法——“立——破”思维，在实际教学中取得很好的效果,所谓“立——破”就是对物理知识先给学生确立一个必须达到的物理达标体系即“立”的过程 ，然后在“立”的基础上要从不同角度，不同层次对这块达标体系进行拓展拔高，即“破”的过程，与传统的拔高的区别在于，这种拔高要有巧劲，要在你的“破”的过程中学生能醍醐灌顶，恍然大悟.这种拔高要有特色，要在你的“破”的过程中学生能感觉到与众不同，回味无穷.下面就以一些具体例子来浅谈“立——破”思维.

1 机械效率习题课的“立——破”思维

例2一花瓶质量约为250kg.为了便于搬运，工作人员先用质量约为50kg的包装箱对花瓶进行包装；然后用两根粗钢管在高1.2m的车厢与地面之间搭成一个长度约为4.8m的简易斜面.装车时，工作人员要用1000N沿平行于钢管方向的推力把包装好的花瓶匀速推上车.求：(1)对花瓶做的有用功?(2)搬运花瓶的机械效率?(3)克服摩擦做的额外功?

对于这道题，学生往往对第一问就出问题了，为什么会出现这个问题呢？问题出在“立——破”上.先说说“立”，机械效率中基本的达标线，学生对用斜面拉高物体，有用功等于重力乘以物体移动的高度，总功是人用的力乘以沿这个力方向移动的距离，额外功等于总功与有用功之差.学生在“立”的过程中往往对定义理解不到位，比如用机械拉高物体时对重力的理解，许多同学理解不到位，会将题目背景中的所有重力全部代入，这是有问题的；现在说说“破”，何为有用功，其实就是你使用斜面的目的，这是需要学生理解的，不能死记公式，例如上题中克服包装纸重力做的功是不是有用功，学生自己要思考这个问题，如果认为是，那就留下花瓶拿走包装纸，学生肯定不同意，所以包装纸并不是目的，花瓶才是，包装纸只是为了保护花瓶是不得不做的功，即额外功.所以对拉高物体的有用功中的重力的理解是需要打破之前的“立”而“破”出新意，于此类似的便是经典的在井中捞水桶问题，如果目的是捞水桶，那克服水桶重力所做的功便是有用功，克服水桶中的水的重力所做的功便是额外功.如果换个情景，目的是用水桶打水，那克服水桶重力所做的功便是额外功，克服水桶中的水的重力所做的功便是有用功.

例3利用动滑轮提升一个重为G的物块，不计绳重和摩擦，其机械效率为60%.要使此动滑轮的机械效率达到90%，则需要提升重力为G的物块的个数为几个？

对于这道题，“立”要求学生必须掌握机械效率是有用功占总功的百分比.但对于这道题我们可以这样“破”——额外功占总功的百分比，即逆向思维，该题中第一次效率为60%，那逆向思维，额外功占总功的比值为40%，就很容易的发现第一次物重和动滑轮为3:2.同样第二次效率为90%，那逆向思维，额外功占总功的比值为10%，第二次物重和动滑轮为为9:1，由于该题中是用同一个滑轮组将不同物体提升相同高度，又不计绳重和摩擦，所以额外功全部来自克服动滑轮自重而产生的功，两次大小是一样的，所以我们可以将第二次物重和动滑轮为9:1变为18：2.这样就会发现额外功相同时，第二次提起的物体重力与第一次提起的物体重力之比为18：6，为3：1，直接得到3块的答案.学生需要打破有用功占总功的百分比，而想到额外功占总功的百分比，“破”出思维火花.对于学习能力强的学生我们需要在已突破的体系下再突破，例如下面这道题.

例4某建筑工地上，起重机的吊臂部分为滑轮组,现用该起重机将质量相同的水泥板吊往高处.若第一次、第二次、第三次分别将一块、两块、三块水泥板吊往某高处，三次起重机做的额外功分别为3000J、4000J、5000J，机械效率分别为η1、η2、η3，则下列关系式正确的是( ).

A．η1>η2>η3B．2η2>η1+η3

C．2η2=η1+η3D．2η2﹤η1+η3

这道题可以尝试让学生在前面已有的突破基础上，再突破到数学思维巧解这个层面上，如图1是物体重力和滑轮组机械效率的关系图像，我们只要在这副图像的基础上合理代值，例如提一块水泥板带机械效率为50%，有图像可知，用滑轮组提高物体，所提物体越重，机械效率越大，则提二块水泥板带机械效率可以赋值为60%，按照图像走势，我们会发现虽然物体越重，机械效率越高，但是由于机械效率不能达到100%，所以随着物体重力的增加，机械效率的增大的幅度会渐渐减小，即η3-η2<η2-η1，所以提三块水泥板带机械效率赋值必须小于70%，可以赋值为65%，将三个机械效率建立联系可以轻松得到答案B.我们要根据自己学生的实际情况去判断孩是止步于“立”，还是可以“破一”或者是“破二”，需要找到最适合自己学生的习题课方案，适合的才是最美的，才可以培养和保护学生的学习兴趣.

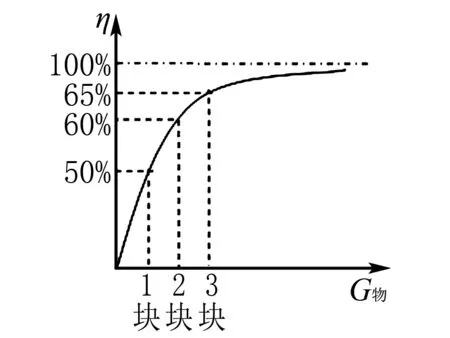
图1

2 压强习题课的“立——破”思维

例5一质量为2 kg、厚度均匀的圆柱形容器，放在水平桌面上，与桌面的接触面积为0.01m2.现往容器内注入0.2 m深的酒精，此时桌面受到的压强为3.2×103Pa (ρ酒精=0.8×103kg/ m3).求：(1)桌面受到的压力；(2)酒精对容器底部的压强；(3)酒精对容器底部的压力.

对于压强计算，先说说“立”，学生必须掌握固体压强一般F=G，P=F/S.液体压强一般P=ρgh,F=PS.如何“破”，学生对这几个公式要正确理解，它们其实没有必须用于固体或液体，四个式子中P=F/S和F=PS是压强的通用计算公式，固液体都可以用，没有条件限制，而公式F=G是可以用在液体中的，公式P=ρgh也可以用到固体中，只不过有适用条件--规则柱状均匀物体.上题中如果学生不能打破这层壁垒，只是按部就班的代公式，由于容器厚度内外面积的不同，最终造成错误，这道题固体最终用了F=PS，而液体却用了F=G.所以我们必须帮助打破对于压强计算公式的思维定式，我们要给学生打破壁垒，帮助学生灵活运用公式.

例6一密度为ρ的钢制轴承，由粗细不同的两部分圆柱体构成，粗细圆柱体的高度均为h.如图2甲所示放置时，轴承对水平面的压强为1.2ρgh,如图2乙所示放置时，轴承对水平面的压强为多少.

图2

这道题目中对桌面的压强，两种放法物体整体都不是规则柱状均匀固体，原则上是不能用P=ρgh求固体压强.适用条件不满足，如何创造条件运用P=ρgh求固体压强，如果我们通过挤压上面的物体的方法可以将物体变为规则柱状均匀固体，也可以通过挤压下面的物体的方法可以将物体变为规则柱状均匀固体，两种挤压方法都可以将上下不是柱状的固体变为上下柱状的固体，那应该采用哪种方法呢？我们回到压强的通用公式P=F/S，不管如何挤压也不能和这个通用公式相矛盾，也就是说你要保证所求的压强处的接触面积和压力在挤压过程中不能出现变化，按照这个想法，我们会发现上面两种挤压方法都不会改变压力，但是通过挤压下面的物体的方法可以将物体变为规则柱状均匀固体的方法会改变物体与桌面的接触面积，而通过挤压上面的物体的方法可以将物体变为规则柱状均匀固体不会改变物体与桌面的接触面积.所以应该挤压上面，挤压之后就可以运用公式P=ρgh，由于物体密度为定值，而P=1.2ρgh，所以挤压之后总高度为1.2h，下面粗的圆柱体高为h，所以高度为h的细的圆柱体由细变粗后高度变为0.2h,在体积不变的前提下，细圆柱体高度减小了5倍，底面积应该扩大5倍，便可以快速找到粗的底面积是细的底面积的5倍，对于图2乙，同样在保证与桌面的接触面积不变的前提下，也可以通过挤压上面的物体的方法可以将物体变为规则柱状均匀固体，即把上面的粗圆柱体挤压成与下面细圆柱体一样粗的圆柱体，粗圆柱体底面积缩小5倍，高度就应该增加5倍，变为5h，在加上下面细圆柱体的高度h，总共6h,从而运用公式P=ρgh，快速得到如图2乙所示放置时，轴承对水平面的压强为6ρgh，运用这种挤压变形最重要是要保证所求压强处的接触面积要保持不变，利用挤压将不是规则柱状均匀的固体变为规则柱状均匀固体，从而利用P=ρgh快速解出题目，获得成就感，我们老师要根据自己、学生、学校的实际情况，是让学习有困难的学生掌握固体压强一般F=G，P=F/S.液体压强一般P=ρgh,F=PS.一般学生要突破到公式的灵活运用，再有能力的孩子让他创造条件用公式.让不同层次的孩子都有所获，有所感，收获成功和喜悦.习题课中的“立——破”思维则是在习题课中的分层教学，教师课前的工作会更多，即要合适高效的分层，更要针对自己的学生有特色的设计习题课.

我们要研究习题课的设计，这是对学生学习物理的负责，也是对学生未来的负责.我们要通过习题课巩固加强学生学习物理的兴趣，不能让习题课只是机械加强巩固学生的基础知识与基础技能，而应该是定位准确，合理立破，层层递进，让不同层次的学生都有收获，都有发展，都能收获幸福感，从而提高学生学习物理的兴趣.这样一来，习题课会变成学生学得开心，老师教得顺心的欢乐海洋.