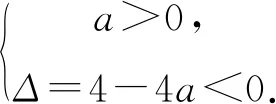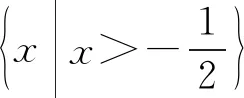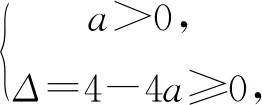聚焦“指数、对数函数”常见解题误区
2023-03-18文丽娜
文丽娜
(甘肃省陇南市康县第一中学 746500)
本文对指数函数和对数函数的常见解题误区加以归类解析,旨在帮助同学们全面准确地理解、认识指数函数和对数函数的图象与性质,有利于积累解题经验,避免一些常见差错的产生,进而提高处理此类问题的技能技巧.
1 未注意对数函数的定义域而致错
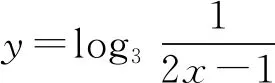
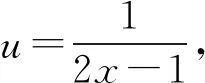

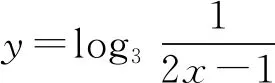
反思一般地,求解与对数函数y=logax有关的函数的定义域和单调区间时,应优先考虑其本身的约束条件x>0;否则,极易出错.
2 未注意指数函数的值恒大于零而致错
例2已知函数y=9x+2·3x+2,x∈R,求函数的值域.
错解令t=3x,则因为y=t2+2t+2=(t+1)2+1≥1,故所求函数的值域为[1,+∞).
剖析错解的根源在于:误认为t∈R,从而(t+1)2+1≥1.而实际上,因为当x∈R时,t=3x>0,所以(t+1)2+1>2.
正解令t=3x,则因为t>0,所以y=t2+2t+2=(t+1)2+1>2,故所求函数的值域为(2,+∞).
反思一般地,换元之后,要注意分析新元的取值范围.特别地,若a>0,x∈R,则必有ax>0.
3 未注意函数的图象有渐近线而致错
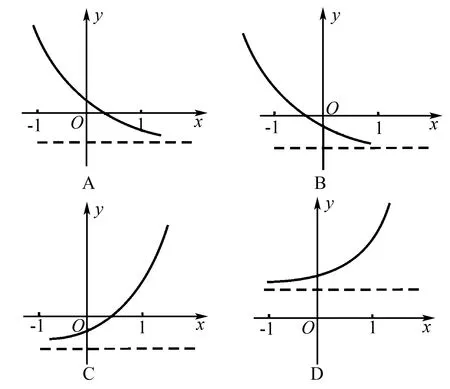
例3 设0 错解如图1,在同一坐标系内分别作出曲线y=|ax-1|和直线y=2,则因为曲线与直线有2个不同的交点,而交点的横坐标就是原方程的实数解,所以原方程的不同实数解共有2个. 图1 图2 剖析错解的根源在于:没有注意到指数函数y=ax的图象有渐近线——x轴,即直线y=0,从而所作曲线y=|ax-1|的图形不准确,由此导致错误的产生. 正解如图2,首先准确作出曲线y=|ax-1|的图形,注意在y轴右侧的图形有渐近线y=1;然后再作直线y=2,则由图观察即知原方程的不同实数解共有1个. 反思一般地,利用指数、对数函数的图象解题时,要注意准确作图是解题的关键所在. 图3 反思一般地,遇到二次函数与指数函数、对数函数在图象方面的交汇问题时,要注意认真观察函数的图象,灵活运用函数的特性,加以准确分析. 错解(1)由原不等式变形得log3a(x-1) (2)错解的根源在于:分析t的取值范围时,误以为指数函数t=ax在[-1,1]上单调递增.而实际上,因为底数a>0,且a≠1,所以指数函数t=ax在[-1,1]上的单调性不确定,故应加以讨论分析. (2)当a>1时,同错解可得a=3. 反思①利用指数函数、对数函数的单调性解题时,首先要注意考查底数与“1”的大小关系,若不确定,则应分情况讨论.②一般地,若常数a>1,则有logax>logay⟺x>y>0;若常数0 例6 若函数f(x)=ln(ax2+2x+1)的值域为R,求实数a的取值范围. 剖析当真数大于零时,并不能保证真数一定取遍所有的正数,从而对应函数的值域也就不一定是R.例如:函数y=lg(x2+1)中真数x2+1≥1>0,但对应y≥lg1=0,即函数的值域是[0,+∞),显然就不是R.上述错解,实际上是分析了当函数f(x)的定义域为R时,实数a∈(1,+∞). 正解依题设,应使函数g(x)=ax2+2x+1的函数值取遍所有的正数. 综上可知,所求实数a的取值范围是[0,1]. 反思本题分析的关键在于以下两点,一是由题设得到必须满足对数的真数ax2+2x+1的值要取遍所有的正数;二是必须按a=0和a≠0进行具体的讨论分析. 以上,通过“借误导悟”的形式,具体阐明了在处理有关指数、对数函数问题中经常会遇到的一些解题误区,能够帮助同学们加深对指数、对数函数的图象和性质的再理解与再认识.同时,也能够较好地提升同学们在直观想象、数学运算以及逻辑推理方面的核心素养.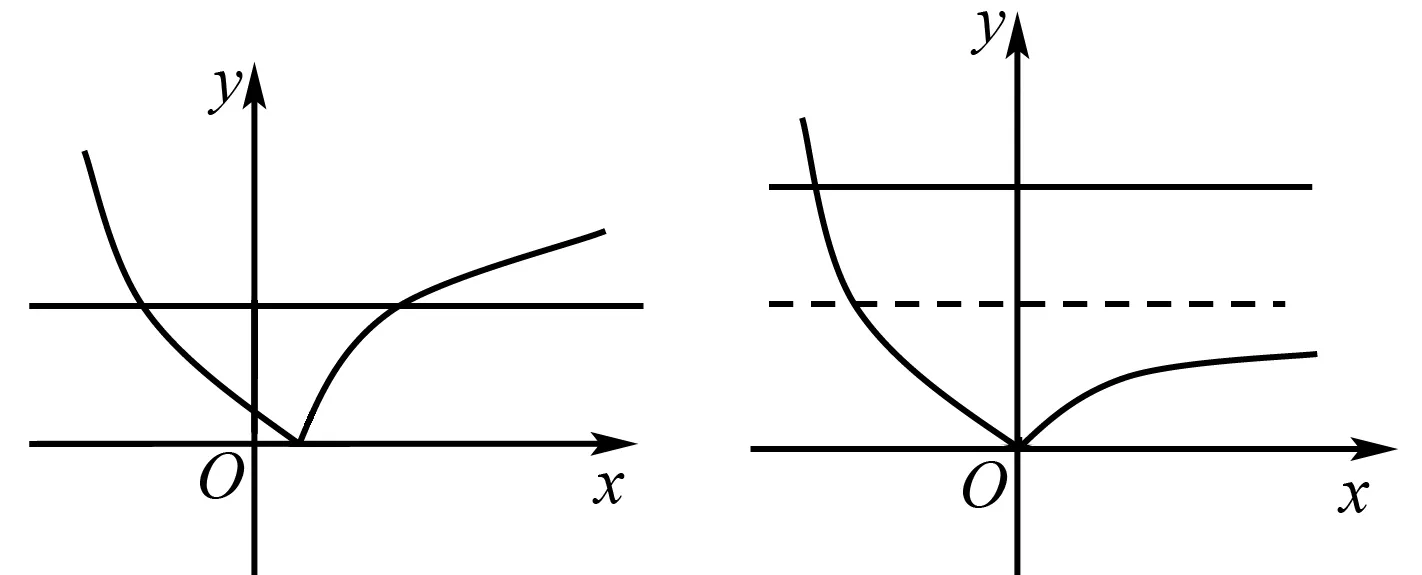
4 未注意函数特性的灵活运用而致错


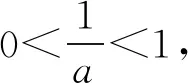
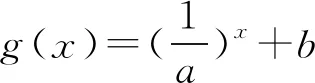
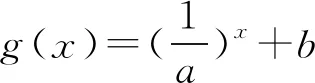
5 未注意底数对函数单调性的影响而致错

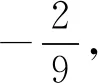
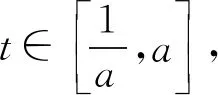
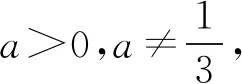

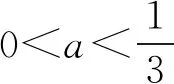

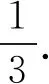
6 未注意对数函数的值域为R必须满足真数取遍所有的正数而致错