一种基于多种群遗传算法的唯相加权阵列波束展宽技术

蔡振龙, 高 坤, 韩彦中, 苏龙阁, 崔艳明

(1.中国电子科技集团公司第五十四研究所, 河北 石家庄 050081;2.西安电子科技大学 物理与光电工程学院, 陕西 西安 710071;3.陆军装备部驻石家庄地区第一军代室, 河北 石家庄 050081)

0 引言

传统脉冲多普勒雷达采用机械扫描天线,机械扫描的惯性限制了波束扫描速度和雷达在多目标跟踪状态所需的波束指向快速扫描,因而极大地限制了雷达的多目标跟踪能力,一般在较高精度下,仅能跟踪2 个目标。 要克服以上缺陷,雷达首先必须实现快速的波束扫描和捷变,因而采用电子控制波束指向的相控阵天线应运而生[1]。

一般情况下,相控阵雷达天线是通过控制天线中辐射单元的幅度和相位来改变天线方向图形状,即实现天线波束宽度、副瓣电平、零陷位置及增益的变化,使相控阵雷达具有更灵活的空域滤波与空时自适应处理能力。 因此,相控阵雷达天线波束形成技术是国内外研究的重要课题之一。

天线波束形状的捷变能力是相控阵雷达的特点之一。 它可以依靠改变相控阵天线的复加权系数来实现。 对于只有移相器的无源相控阵天线,则可以用“唯相位”(phase-only)的方法,即只改变各单元通道的相位来实现天线波束形状的改变[2]。

所谓相控阵天线波束展宽是要通过改变相控阵天线的相关参数,从而改变相控阵天线方向图形状,使其展宽主瓣宽度[3]。

天线波束展宽一般采用2 种方法:第1 种方法是调整阵列单元的幅度和相位,即幅度、相位同时加权;第2 种方法是只调整阵列单元的相位,即相位加权。 幅度和相位同时调整加权能得到很好的波束展宽结果,但幅度加权需要增加幅度衰减器,使天线设计复杂度及成本增加。 采用相位加权的方法,通过调整相控阵天线的移相器就能达到相似的效果,因此,在工程应用方面具有较高的价值[4]。

相位加权方法的基本思想是仅仅通过调整、改变相控阵天线的相位,就可完成天线方向图波束的展宽。 为实现天线的唯相波束展宽,国内外研究人员研究、发明了很多展宽波束的方法。 Bucci 等[5]较早提出了唯相方法综合天线方向图,并在波束展宽及赋形设计中获得较好的结果。 Vescovo[6]则利用唯相位方法对圆形阵进行了分析。 Sarma 等[7]采用遗传算法(Genetic Algorithm,GA)对期望形状的方向图进行了设计,取得了较好效果。 Haupt 等[8]利用GA 对基于唯相方法的天线波束控制进行了波束零陷的仿真设计,并在有2 个干扰的情况下获得了预期效果。 文献[9]通过调整相控阵天线的焦距使天线相位散焦,采用外缘邻近单元零法、π 配相法,可实现天线波束宽度的展宽。 文献[10]提出了将一个阵列天线分成2 个子阵列,2 个子阵列主瓣指向设计成不同的方向,2 个不同指向的子阵主瓣波束最终合成为一个波束,可以展宽主瓣的波束宽度。 文献[11-12]描述了一种通过改变天线阵单元相位恶化天线主瓣的平坦度方式,使其在主瓣上产生小于3 dB 的波纹,从而展宽相控阵列天线主瓣波束宽度。 Song 等[13]釆用粒子群算法和GA 求相位关系,得到了所需要的波束展宽效果。 徐慧等[14]则采用了一种新型的基于排序的主动变异性退火-遗传算法(AMAGA)求解相位关系[15]。 安怀彬等[16]通过理论分析、计算、仿真和实际测试,表明其采取外缘单元“0、π 随机配相法”进行波束展宽的工作满足了其实际工程要求。 高世超等[3]在幅度加权的基础上,通过相位加权实现对特定波束的展宽。王艳温[17]基于相位加权,提出了一种旁瓣抑制方法,通过搜索寻找到降低旁瓣及主瓣展宽程度的多约束条件,并将求得的加权向量投影到基于特征结构的投影矩阵上,对该算法进行了仿真,验证了算法的可行性,并分析了仿真结果,指出了算法的优点与不足。 毛小莲[18]为实现相控阵雷达天线在俯仰面波束的展宽,采用GA 对各单元的馈电相位分布进行优化,实现了方向图的波束展宽,并较好地控制了副瓣电平;此外,还对展宽的波束进行了扫描,并通过移相器控制波束展宽和扫描。

上述各类算法均可实现相控阵天线波束展宽,但也存在算法性能降低等现象。 本文采用多种群遗传算法(Multiple Population Genetic Algorithm,MPGA)的唯相加权阵列波束展宽技术,很好地实现了阵列天线波束的展宽。

GA 是一种全局优化搜索算法,以自然选择和遗传学机理理论为基础,是一种通过模拟自然进化过程搜索最优解的方法[19]。

GA 是从任一初始种群开始,通过随机选择、交叉和变异的操作,按照适者生存、优胜劣汰的原理,演化产生出近似最优解的智能算法[20-21]。

GA 是一种群体型操作,以群体中的所有个体为对象[22-23]。 跟一些其他优化算法相比,具有全局、并行搜索的特点,局部不容易出现最优解,并且与传统的搜索处理方法相比,不依赖于问题的梯度信息,所以特别适合于解决各类复杂及非线性问题。因此,在诸如模式识别、工程优化等[24]很多领域得到了应用,也同样适用天线研制过程中面临的类似问题。

标准遗传算法(Standard Genetic Algorithm,SGA)存在运算优化精度不够、局部搜索能力差以及运算结果过早收敛等缺点。 为弥补SGA 的不足之处,研究人员采用多种措施,包括运用多种群算法、动态编码技术、自适应遗传算法和小生境聚类技术等。 验证结果表明,这些改进措施和方法一定程度上提高了GA 的性能[24]。

运用适应度函数的GA 在数据搜索和生成上具有一定的盲目性,存在运算结果过早收敛,即容易陷入早熟,进而在运算求解过程中出现局部最优解的现象;同时,传统算法收敛速度则较为缓慢[25]。

由天线的基本理论可知,天线波束的展宽在一定程度上会影响天线的其他性能指标:一方面,天线波束的展宽会导致天线的主副瓣比产生变化。 对雷达而言,如果天线的主副瓣比变差,其抗干扰能力将受到一定程度的影响;另一方面,天线波束的展宽,如果保持主副瓣比不发生变化,则会引起主瓣增益的下降[26],降低雷达的探测威力。 上述问题彼此交联,互相影响。 若得不到较好的解决,顾此失彼,那么天线波束的展宽就不存在工程意义[3]。

本文针对上面所述的2 个问题,基于天线波束展宽的理论,进行了着重分析和研究,并提出了解决方法。 并以均匀直线阵列和扇形圆环阵列为研究对象,结合其数学模型,应用MPGA,通过唯相加权方法最终实现了阵列方向图的波束展宽。 仿真结果表明,该方法可以在充分考虑到副瓣电平及天线效率的前提下,形成更宽的波束宽度,且收敛速度较快,稳健性较好,预示了遗传算法在阵列天线设计中广泛的应用前景。

1 MPGA 介绍

SGA 流程如图1 所示。

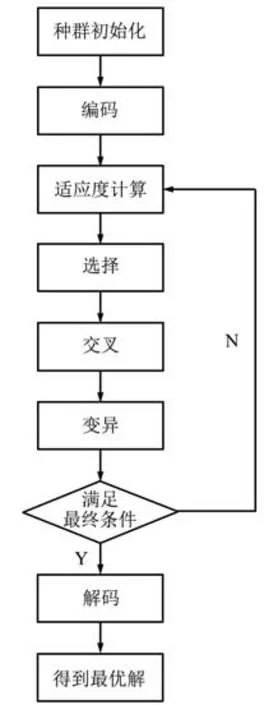
图1 SGA 流程Fig.1 Flowchart of SGA

SGA 中运算结果未成熟而过早收敛现象主要表现在群体中的所有个体都趋同于同一状态而停止进化,算法最终运算结果不能满足要求。 经研究分析,未成熟而过早的收敛主要跟下列因素有关:

① 选择操作是根据当前群体中个体的适应度值所决定的概率进行的,当群体中存在个别超常个体时,该个体在选择算子的作用下多次被选中,下一代群体很快被该个体所控制,新群体失去竞争性,从而导致群体停滞不前;

② 交叉概率PC和变异概率Pm的取值最终影响进化搜索的结果,而且非常敏感,不同的取值可能导致不同的计算结果;

③ GA 的寻优性能对群体规模的要求很高,群体的规模小,群体中的多样性就差,群体中的个体随着竞争性变弱进行进化时很快趋于单一化,群体很快将终止进化;

④ GA 常用的终止判据是,当迭代次数到达人为规定的最大遗传代数时,则终止进化。 GA 迭代次数过少,进化不充分,将会造成未成熟收敛。

为弥补SGA 的不足,针对以上GA 存在的问题,本文引入了一种基于MPGA 的设计方法,可以有效地克服标SGA 在诸多方面的缺陷。

MPGA 运用多种群并行进化的方法,同时对多个种群并行进化。 其中主种群中引入辅助种群或者修正种群中的部分优良个体参与进化,从而打破主种群的平衡态,进而达到更高的平衡态[27]。

MPGA 不依赖SGA,仅靠单个群体进行遗传进化的模式,同时引入多个种群进行优化搜索,对多个种群选取不同的控制参数,从而实现不同的搜索目的。

各个种群之间通过移民算子取得联系,进行多种群的协同进化。 在进化过程中出现的最优个体通过移民算子定期地引入其他种群中,从而实现各种群之间的信息交换。

MPGA 结构示意如图2 所示。

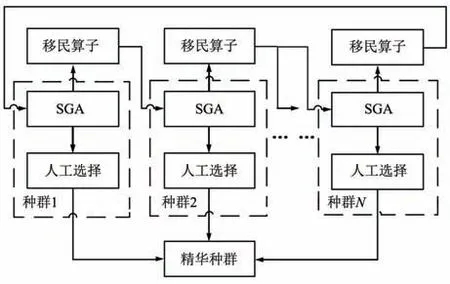
图2 MPGA 算法结构示意Fig.2 Structural representation of MPGA

通过利用人工选择算子选出各种群中的最优个体,放入精华种群中并保存起来,精华种群不参与选择、交换和变异等遗传操作,以保证进化过程中各种群产生的最优个体不被破坏和丢失。 精华种群可以作为判断算法的依据,采用最优个体最少保持代数作为终止判据依据[28]。

综上所述,MPGA 弥补了SGA 的众多不足,通过引入并行进化、移民算子和人工选择算子等设置多个控制参数,实现种群协同进化,同时兼顾了算法的局部和全局搜索。

2 MPGA 在阵列波束展宽上的应用

2.1 适应度函数的选择

如引言所述,有源发射天线阵列为了获得更宽阔的空域覆盖效果,需要对天线阵列的方向图进行波束展宽,且需同时兼顾副瓣电平和天线效率;特别是对于雷达应用而言,为获取最大的等效辐射功率(EIRP)值,其发射组件大多工作在饱和区,即其单元幅度因饱和输出不可调节,因此只能对天线阵列各单元的相位进行调节,以满足波束展宽需求。 在处理解决对该工程问题时,传统遗传算法容易陷入局部最优解的缺点导致波束展宽效果不太理想。 本文应用MPGA 对该工程问题进行优化求解,并探讨其工程应用验证前景。

致力于天线的波束展宽且忽视对副瓣电平的控制,将使雷达的抗干扰能力受到影响;而天线波束展宽,天线增益将会下降,又会影响到雷达的探测能力。 所以,在适应度函数的编写上,不仅要涵盖对波束宽度的控制规则,同时也要对副瓣电平进行控制。

综上所述,本文对适应度函数的编写规则如下:

式中,BW为波束宽度;iBW为理想的波束宽度;SLL为副瓣电平;iSLL为理想副瓣电平;w1为波束宽度的权值;w2为副瓣电平的权值。

不同的权值w1,w2,对方向图的侧重也不同,若增加w1则可以提高对波束宽度的控制力度;同样,增加w2则可以提高对副瓣电平的控制力度;通过对权值w1,w2的合适选取,可得到尽可能满足所期待结果的方向图。

2.2 工程实例应用

2.2.1 应用实例1:均匀直线阵列

基于工程需求,现设定某一维N元均匀直线发射阵列,各天线单元后端连接对应发射组件,发射组件饱和输出,其输出功率值一致;工程需求为仅通过调节单元相位达到该一维线阵波束展宽的目的,且在增加波束覆盖范围的同时兼顾副瓣电平和线阵EIRP 值。

对于该一维N元均匀直线发射阵列,其模型如图3 所示。

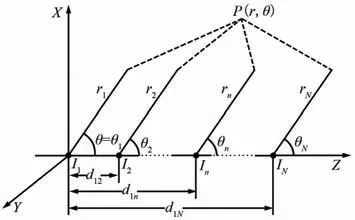
图3 一维N 元均匀直线阵列模型Fig.3 One-dimensional N-element uniform linear array model

阵列内各天线单元之间的间距相等,均为d,即d12=d;d1n=(n-1)×d;d1N=(N-1)×d,阵列方向图为:

式中,fa(θ)为天线的单元因子;N为单元数目;In表示第n个单元的馈电电流(加权系数);d为单元间距;k为波数;θ为扫描角度;Φn为第n个单元的相位。

对于单元数目为N,频率为f0,单元间距为d的一维均匀直线阵列,应用SGA 和MPGA 对每个单元的相位进行加权,以此实现该一维均匀直线列的波束展宽,每个个体采用二进制编码,每个基因的编码长度为10,N个单元的加权相位左右对称。 应用SGA 时,迭代次数为300,每代种群规模为200;应用MPGA 时,每个种群的最优值至少保持10 代。

为与以上2 种相位加权结果进行比较,对于该一维N元均匀直线发射阵列,对于无相位加权时的情况,也做了相应仿真。

以下是对上述3 种情况的仿真结果对比。 基于SGA 和MPGA 的唯相加权方向图对比如图4 所示。基于SGA 和MPGA 的进化曲线对比如图5 所示。根据图4 的仿真结果,针对一维N元均匀直线阵列,无相位加权、应用SGA 对每个单元的相位进行加权、应用MPGA 对每个单元的相位进行加权,仿真结果从波束宽度、副瓣电平和天线增益等维度进行对比,对比情况如表1 所示。

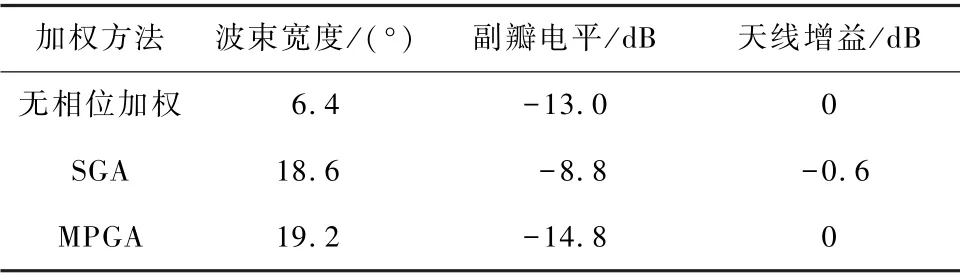
表1 一维N 元均匀直线阵列仿真结果对比表Tab.1 Comparison of simulation results of one-dimensional N-element uniform linear array

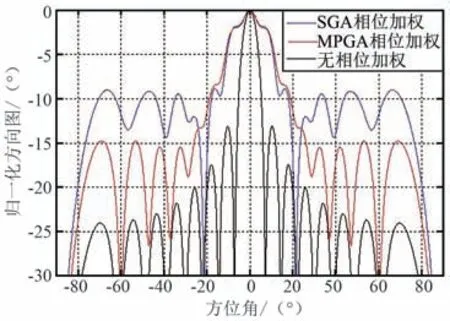
图4 基于SGA 和MPGA 的唯相加权方向图对比Fig.4 Comparison of patterns based on SGA and MPGA by phase-only weighting

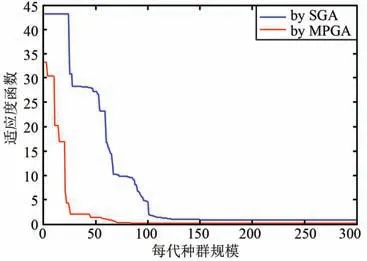
图5 基于SGA 和MPGA 的进化曲线对比Fig.5 Comparison of the trace to iterative convergence based on SGA and MPGA

图4 及表1 表明,相对于无相位加权,应用SGA进行唯相位加权波束展宽,虽然很好地实现了波束宽度2.9 倍的展宽,但是对于副瓣电平来说,具有将近4.2 dB 的恶化,对于天线增益来说,也有0. 6 dB的恶化;应用MPGA 进行唯相位加权波束展宽,不仅很好地实现了波束宽度3. 0 倍的展宽,而且兼顾了副瓣电平1.8 dB 的优化,同时保证了天线增益基本无损失。 并且从图5 的迭代收敛曲线可以看出,应用MPGA 算法收敛速度更快,仅70 代就寻找到全局最优解从而达到收敛,而应用SGA 算法的收敛速度较慢,且容易陷入局部最优解。

2.2.2 应用实例2:扇形圆环阵列

基于某一战场通信指示雷达的有源阵列天线的工程需求,其组阵形式为扇形圆环阵列,模型如图6所示。

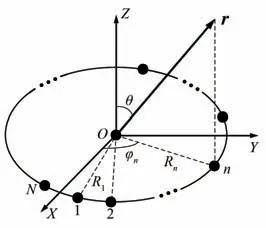
图6 圆环阵模型Fig.6 Ring array model

考虑如图6 所示的扇形圆环阵列,围绕圆环中心在半径R处等环距放置N个阵列单元,每个单元坐标记为(Xn,Yn,0),其中n为单元在阵列中的序号,全阵的单元总数为N。 则对远场矢位r处来说,若阵列等幅同相激励时,方向图函数为:

式中,k为波数;fn(θ,φ)为第n个单元的方向图;θ,φ分别为波束扫描方位及俯仰角度;(Xn,Yn,0)为每个单元坐标;r为单位矢量;ex,ey分别为圆环阵坐标系x,y轴对应的单位矢量;Φn为第n个单元的馈电相位。

考虑到各个单元并非全向辐射,故有:

式中,Rn为第n个单位距圆环中心的距离;Φn为第n个单元的馈电相位。

考虑工程实际情况,该扇形圆环阵列在方位一圈的单元总数为N,当有源相控阵工作时,实际工作时的方位波束指向要求为方位某一固定指向,同时参与工作的单元数目为num;根据扇形圆环阵列的使用要求,只考虑方位角φ方向的方向图,故θ=π/2,阵列满阵单元数目N,工作频率f0,使用单元数目为num,圆环半径为r=R。 根据此模型按上述实际的工程考虑,可以将式(3)简化为:

根据扇形圆环阵列模型,应用GA 对式(5)中的每个单元的相位进行加权,以此实现扇形圆环阵列的波束展宽,令num个单元的加权相位左右对称,单个个体采用二进制编码,每个基因的编码长度为10,选取10 个种群,每个种群最优值至少保存10代,并进行仿真。

为与以上2 种相位加权结果进行比较,对于该扇形圆环发射阵列,按照无相位加权情况,也做了相应仿真。

对于该模型,在无相位加权、应用SGA 进行唯相位加权、应用MPGA 进行唯相位加权3 种情况下的仿真结果如图7 所示。

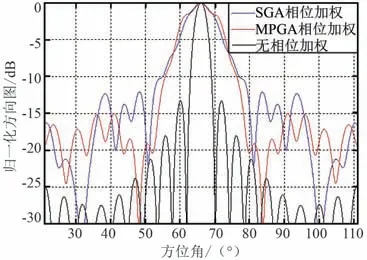
图7 基于SGA 和MPGA 唯相加权方向图对比Fig.7 Comparison of patterns based on SGA and MPGA by phase-only weighting

根据图7 所示的仿真结果,针对扇形圆环阵列,无相位加权、应用SGA 对每个单元的相位进行加权、应用MPGA 对每个单元的相位进行加权的仿真结果从波束宽度、副瓣电平和天线增益等维度进行对比,对比情况如表2 所示。

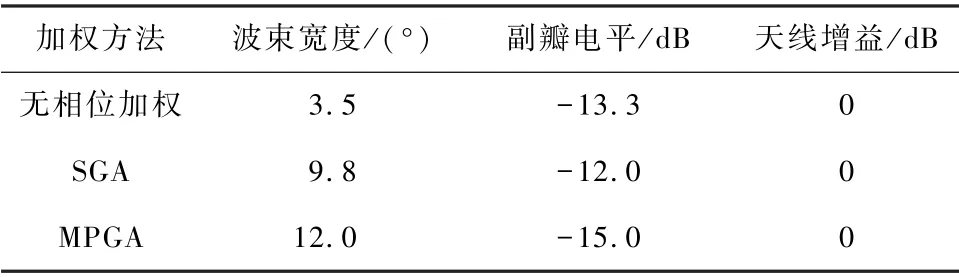
表2 扇形圆环阵列仿真结果对比表Tab.2 Comparison of simulation results of fan-shaped ring array

图7 及表2 表明,相对于无相位加权,应用SGA进行唯相位加权波束展宽,虽然很好地实现了波束宽度2.8 倍的展宽,但是对于副瓣电平来说,具有将近1.3 dB 的恶化;应用MPGA 进行唯相位加权波束展宽,不仅很好地实现了波束宽度3.4 倍的展宽,而且兼顾了副瓣电平1.7 dB 的优化,同时保证了天线增益基本无损失。 并且从图8 的迭代收敛曲线可以看出,应用MPGA,前几代的收敛速度非常快,仅45代就寻找到全局最优解从而达到收敛,而应用SGA的收敛速度较慢,计算效率仅为MPGA 的33%。

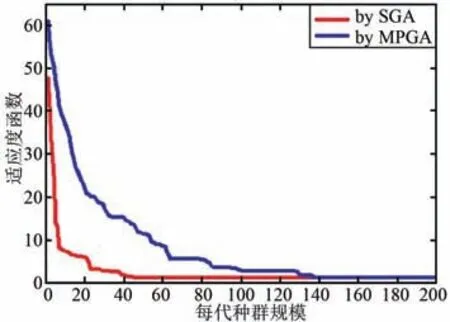
图8 基于SGA 和MPGA 的进化曲线对比Fig.8 Comparison of the trace to iterative convergence based on SGA and MPGA

3 结论

本文提出了一种基于MPGA 的唯相加权波束宽度展宽的方法,针对一维N元均匀直线阵列和扇形圆环阵列,应用MPGA,分别设计出适配的适应度函数,在充分考虑到副瓣电平及阵列增益的基础上,通过Matlab 仿真,很好地实现了基于该模型的方向图波束展宽,且收敛速度较快,稳健性较好。 相比于传统的SGA,MPGA 虽然计算过程复杂,但在综合考虑并平衡兼顾多个相互制约的技术指标的阵列天线设计中,MPGA 能发挥其同时兼顾局部和全局搜索的优势,可直接用于均匀直线阵列和扇形圆环阵列天线工程设计。