素养视角下初中数学图境图表类应用问题的教学策略研究

蒋明祥

摘 要：图境图表类问题是当今中考命题的一个热点，它是以图象、图形及表格等形式给出信息，通过认真阅读、观察、分析、加工、处理等手段解决的一类实际问题.主要考查同学们的读图、识图、用图能力，以及分析问题、解决问题的能力.因此，帮助学生实现对此类问题的本质的认识，提升学生分析问题、解决问题的能力是急需解决的重中之重.

关键词：阅读理解;读图识图;教学策略

新课标指出，能够运用图表工具表示、分析问题情境中的数量关系建构模型解决问题，探索解决问题的思路^［1］.图境图表类应用问题是大多数学生比较难以“对付”的问题，得分率并不高，主要问题在于三卡：一卡在于读不懂图形，特别是实际图形和函数图形的辨识、融合、整合，二卡在于不会利用方程和建模的思想来解决问题（一次函数、二次函数和反比例函数），三卡在于学生对于这些问题还缺乏系统性的专题训练，没有形成整体的知识建构，所以在教学中教师既要引导学生阅读文本、提取有效信息，挖掘蕴含条件，应用所学知识解决有关问题，还要放慢教学节奏，慢慢引导学生通过自主探究、合作交流、抽象概括，完整经历掌握图境图表中信息的过程，让学生在比较充分的数学活动中，提高分析问题、解决问题的能力，培养数学建模能力.

1 引导学生“识图”，帮助信息整理

所谓图境、图表问题就是根据文字、图象、图表等给出信息提供问题情境，这类题目的解题条件主要靠图象（表）给出，来探求多个变量之间的关系，再综合运用方程、函数、统计等知识加以分析，以解决实际问题的题型.在交流数学思想、推理和发现时，无论是口头还是书面交流均要求恰当地使用数学语言、运用各种不同形式的表示法（用来表达数学信息的各种公式、表格、坐标图、曲线图和模型等），所以应教会学生在理解“图”的基础上，获取有效信息，对已获信息进行加工、整理，理清各变量之间的关系，选择适当的数学工具，通过建模解决问题，实现“识图明境”.

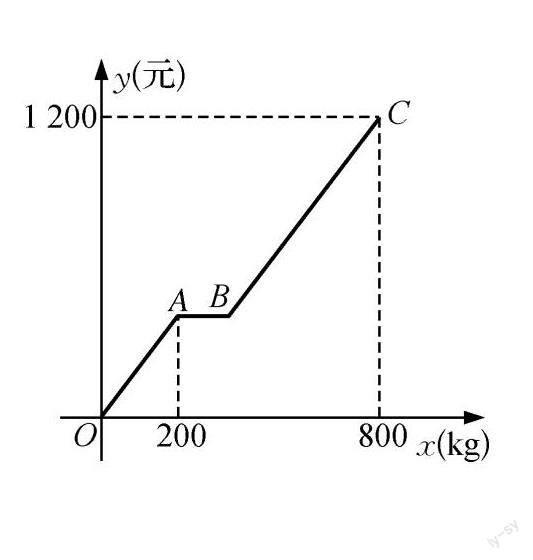
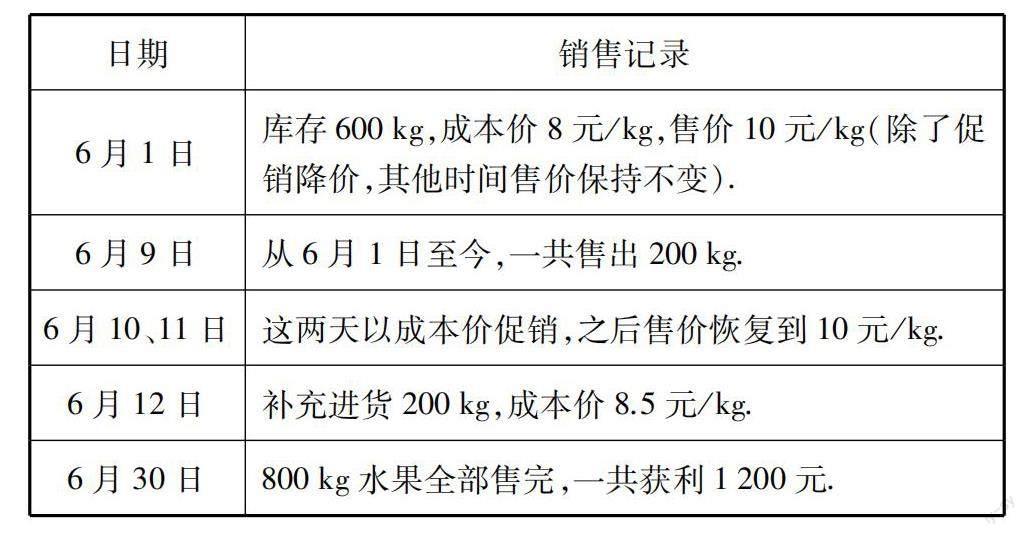
【例】 某商店代理销售一种水果，六月份的销售利润y（元）与销售量x（kg）之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题：

（1）截止到6月9日，该商店销售这种水果一共获利多少元？

（2）求图象中线段BC所在直线对应的函数表达式.

本题是2020年苏州市中考题，常见的利润问题，但是此题中的实际信息以表格的形式反馈，同时又配有一张函数图象，难度提升，对学生的数学阅读能力有较高的要求.表面看求线段BC所在直线对应的函数表达式，实质就是求点B的坐标.第一小题“求解6月9日，该商店销售这种水果一共获利多少元？”关键在于解决B的横坐标，所以引导学生通过假设B的横坐标，寻找方程是本题的突破口，方程的知识点在此题中得以很好的应用，再次让学生感受到方程是解决“图境”问题的“好帮手”.

2 融合数学思想，实现明镜建模

基于方法，源于模型.模型观念有助于开展跨学科主题学习，感悟数学应用的普遍性^［2］..图境图表信息类应用问题往往和“方程（组）、不等式（组）、函数、统计与概率”等知识结合考查，这类试题是指通过图（如图片、图象、图形等）、表（表格、统计表等）以及实物等形式呈现信息，要求答题者通过观察、比较、分析、筛选，从中获取有用的信息，进而建立数学模型，使所给问题得到解决的一类题型.

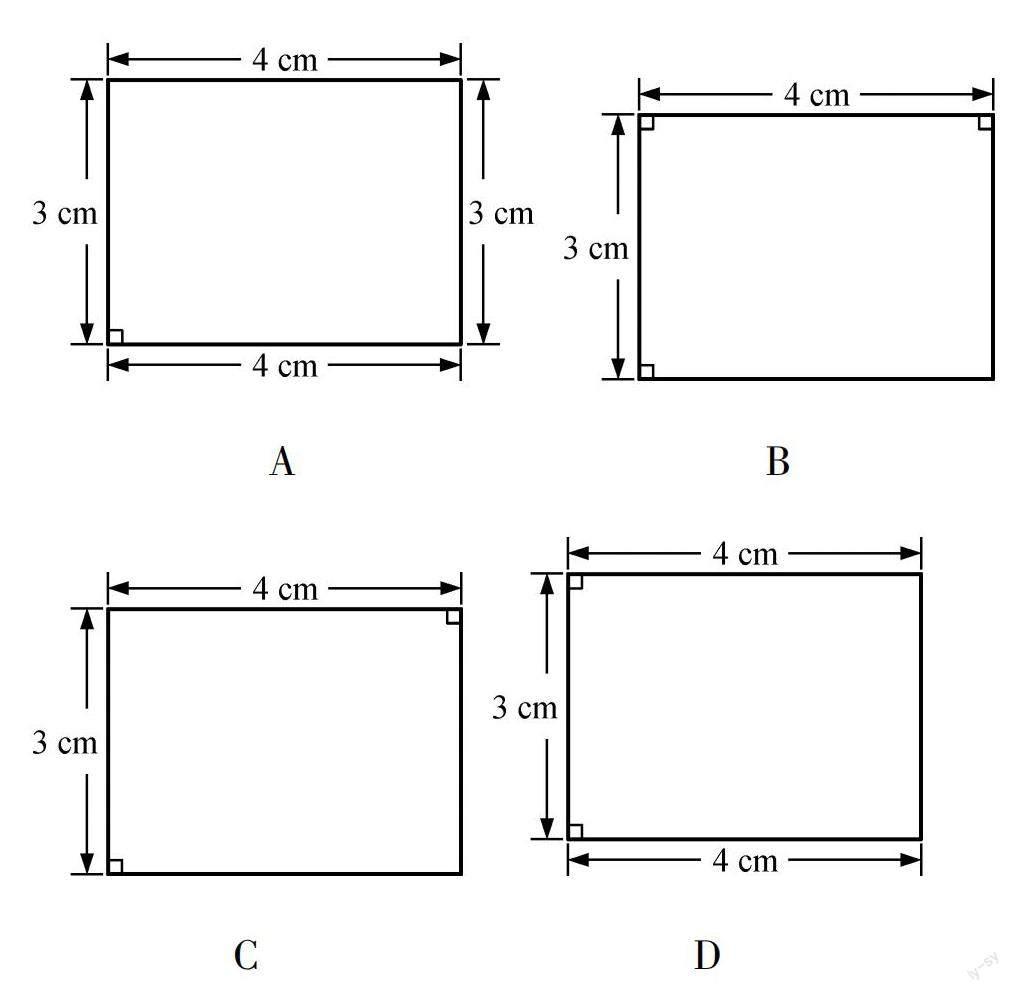
【例】 杨师傅应客户要求加工4个长为4cm，宽为3cm的矩形零件.在交付给客户之前，杨师傅需要对4个零件进行检测.根据零件上的检测结果，下列图形中，有可能不合格的零件是（）.

本题考查图形的认识及矩形的判定等知识和学生图形语言和文字语言的互译能力的掌握情况，要求学生直接利用矩形的判定定理来判断四边形是否为矩形.和常规的方式不同，该题采用了在图形上标注条件的方式，更加直观，贴合实际.从学生作答情况来看，只有46%的同学答对，得分情况不太理想.分析学生的思考障碍，主要有两个：一是看不懂图中的数值和直角标记的意义，二是知道意义但无法和所学定理联系起来.

3 帮助策略提炼，实现知识建构

图境图表类问题是很有价值的数学问题，更能让学生明白学习数学的意义和价值.下面例题是2020年盐城中考的27题，此题能充分体现研究数学的价值，对于建模和模型在现实情境中的运用都体现的很到位，从教学的效果看有部分学生能理解模型的运用和构造，对于尖子生的思维的提升有较大的帮助.在教学过程中，充分让学生自己提炼和反思，也是为了能更好理清此类数学问题的本质，有助于学生自己的体悟和收获，同时展示的结构框架图能更好地帮助学生理清脉络和途径，促进数学能力的提升.终于素养，提升能力，从学生的最近发展区入手，从实践、反思、总结、再实践、提升引导学生探究总结，提炼方法，升华思想.

【例】 以下I-V为一个合作学习小组在一次数学实验中的过程记录，请阅读后完成下方的问题1～4.

（Ⅰ）在Rt△ABC中，∠C＝90°，AB＝22，在探究三边关系时，通过画图，度量和计算，收集到一组数据如下表：（单位：厘米）

（Ⅱ）根据学习函数的经验，选取上表中BC和AC+BC的数据进行分析：

① BC＝x，AC+BC＝y，以（x，y）为坐标，在图①所示的坐标系中描出对应的点；

② 连线；

观察思考

（Ⅲ）结合表中的数据以及所画的图象，猜想：当x＝_______时，y最大；

（Ⅳ）进一步猜想：若Rt△ABC中，∠C＝90°，斜边AB＝2a（a为常数，a＞0），则BC＝_______时，AC+BC最大.

推理证明

（Ⅴ）对（Ⅳ）中的猜想进行证明.

问题1：在图①中完善（Ⅱ）的描点过程，并依次连线；

问题2：补全观察思考中的两个猜想：

（Ⅲ）________；（Ⅳ）________；

问题3：证明上述（Ⅴ）中的猜想；

问题4：图②中折线B—E—F—G—A是一个感光元件的截面设计草图，其中点A，B间的距离是4厘米，AG＝BE＝1厘米.∠E＝∠F＝∠G＝90°.平行光线从AB区域射入，∠BNE＝60°，线段FM，FN为感光区域，当EF的长度为多少时，感光区域长度之和最大，并求出最大值.

本题是中考压轴题，充分体现了“图境”的味道，从表格到函数图象到实物图象，让学生充分感受到生活中有浓浓的数学的味道.此题也很综合，考查了解直角三角形、函数、一元二次方程的根的判别式等知识，但最重要的还是方程和函数的思想运用，特别是对于猜想的证明用函数和方程的方法都可以解决，更体现了两者之间的融合性.通过对此类问题的探究让学生的数学素养有了更大的提升，在解决问题的时候能体会问题的本质，理解题目的用意.让学生在实践中提炼总结，充分发挥学生的主观能动性，自主探究，实现自我成长和数学素养的提升.

简言之，图境图表类问题教学是培养学生应用能力的一条重要途径.在教学中，教师要培养其解决应用问题的学习兴趣与意志，引导学生用数学的眼光认识世界，增强生活中运用数学的体验，熟悉图境图表性问题的实际背景.在学生数学建模能力的培养中，教师既要重视提高他們对题目中关键词语、关键数据和关键图表等信息的理解，清除解决应用问题的障碍，还要不断地提高学生综合运用数学知识解决非常规问题的能力，使学生的数学思维水平达到一个更高的境界.

参考文献：

［1］ 孔凡哲，史宁中.《义务教育数学课程标准（2022年版）》教学活动标准解读［J］.天津师范大学学报（基础教育版），2022，23（6）：21-25.

［2］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.