基于支持向量机的抗干扰决策技术

2023-03-15原浩娟程龙宝冀文辉

上海航天 2023年1期

原浩娟，程龙宝，徐恒，冀文辉

（上海航天电子通讯设备研究所，上海 201108）

0 引言

随着当今电子技术的蓬勃发展，雷达探测区域内的电子装备逐渐形成了种类繁多、体制复杂的特点，因此空间内常充斥着各种电磁信号。现代战场的环境往往突发多变，这些战场的干扰杂波等信号频域密集交叠、空域纵横交错、时域突发多变、能量强弱多样［1-2］。针对雷达信号处理领域中的抗干扰问题，国内外研究者在这方面展开了大量的研究。早期的研究方法主要有副瓣匿隐法、副瓣对消法、自适应副瓣相消法、多径自适应相消法和自适应波束形成法。近年来，研究的主要方法有自适应-自适应数字波束形成技术［3-5］、单脉冲和极大似然算法［6-8］。

面对现代雷达电子战复杂的电磁环境，雷达系统应具有更高的对环境感知的能力。2006 年，HAYKIN［9］提出了认知雷达的概念，认知雷达因具有环境感知力强、可自适应发射处理等优点，被认为是未来雷达系统的一种发展方向。从2009 年开始，美军逐步将认知的概念引入电子战装备中，标志着认知电子战概念的形成［10］。认知电子战系统通过认知对抗环节，根据认知侦察环节识别出干扰类型，自主决策需要采取的抗干扰措施。本文将支持向量机［11］（Support Vector Machine，SVM）引入抗干扰决策系统中，通过对输入样本的训练来得出抗干扰措施预测器，以此提升雷达的抗干扰性能。

1 抗干扰决策系统的输入

雷达在同一时刻侦收到的干扰一般有一种或多种，对于决策系统，输入的参量为只有0 或1 的二进制向量，见表1。

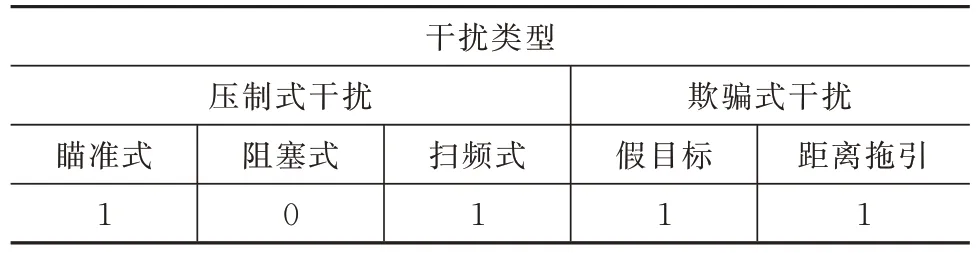
表1 同一时刻雷达侦收到的干扰样式Tab.1 Jamming patterns detected by radar at the same time

由表1 可知，雷达侦收到的干扰有瞄准式噪声干扰、扫频式噪声干扰、假目标干扰和距离拖引干扰，因此输入的向量为［1，0，1，1，1］。决策系统对该输入向量进行分析，在“一对多”原则下，选取一种抗干扰措施来对抗以上多种干扰样式。该抗干扰决策系统也可以运用于“一对一”原则进行决策，当只有一种干扰存在的情况下，可以得到一种抗干扰措施。

在作战前，需要先通过先验知识构建抗干扰决策表，见表2，根据该表可训练抗干扰决策系统。

表2 抗干扰决策表Tab.2 Anti-jamming decision table

训练好抗干扰决策系统后，当雷达侦收到干扰信号，首先通过干扰识别过程得到当前存在的干扰样式，将存在的干扰样式置“1”，不存在的干扰样式置“0”，将0 或1 填入表2 中每种干扰对应的位置生成输入向量，表1 所对应的输入向量为［1，0，1，1，1］。输入向量后，抗干扰决策系统通过，运算和分析输出结果，即针对当前侦收到的干扰样式所决策出的抗干扰措施，该抗干扰措施是当前最优的手段。

在仅有1 个干扰存在的情况下，通过采取该抗干扰措施，即可根据广义电子抗干扰改善因子（ECCM Improvement Factor，EIF）来评估其在当前环境下的有效性。

2 基于SVM 的抗干扰决策系统

SVM 由AT&T Bell Labs 的VAPNIK 及其团队于1995 年提出，一般用于解决分类问题，在少量训练样本的情况下还可获得很好的结果。将样本和样本标记输入SVM 不断训练，得到最优分类线，如图1 所示。此时将新的样本输入SVM，通过最优分类线的判决即可得知新的样本属于红点类还是蓝点类，如图2 所示。

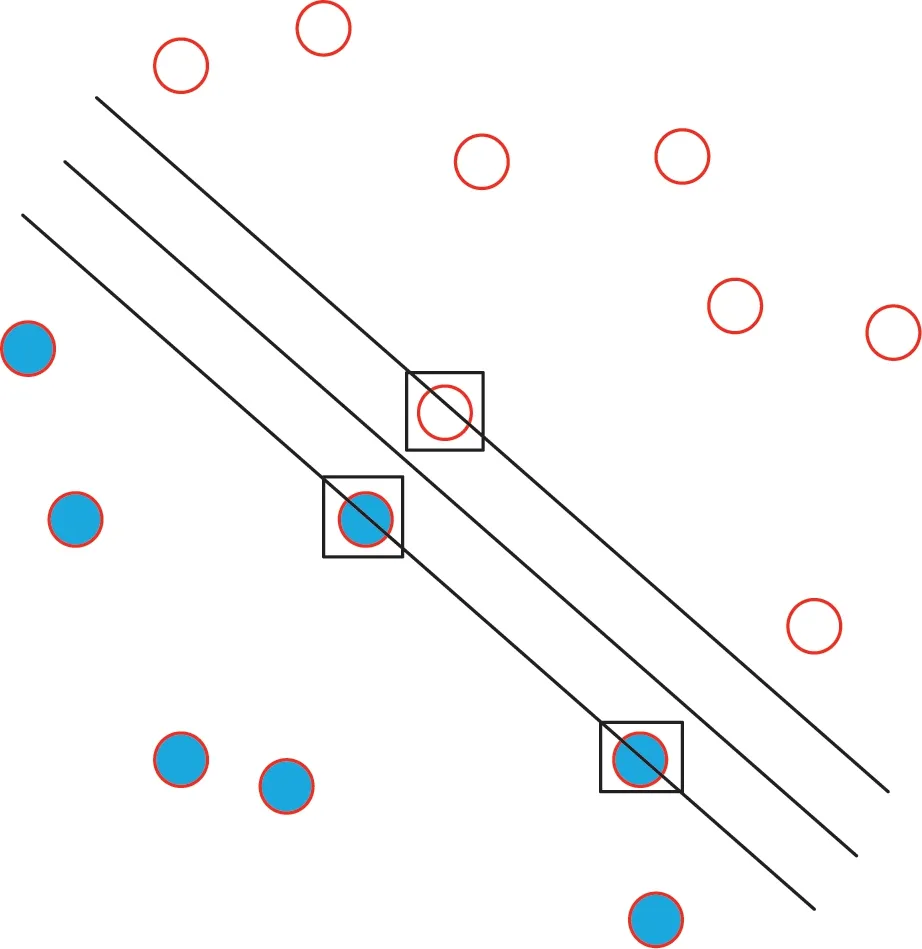
图1 SVM 分类Fig.1 SVM classification

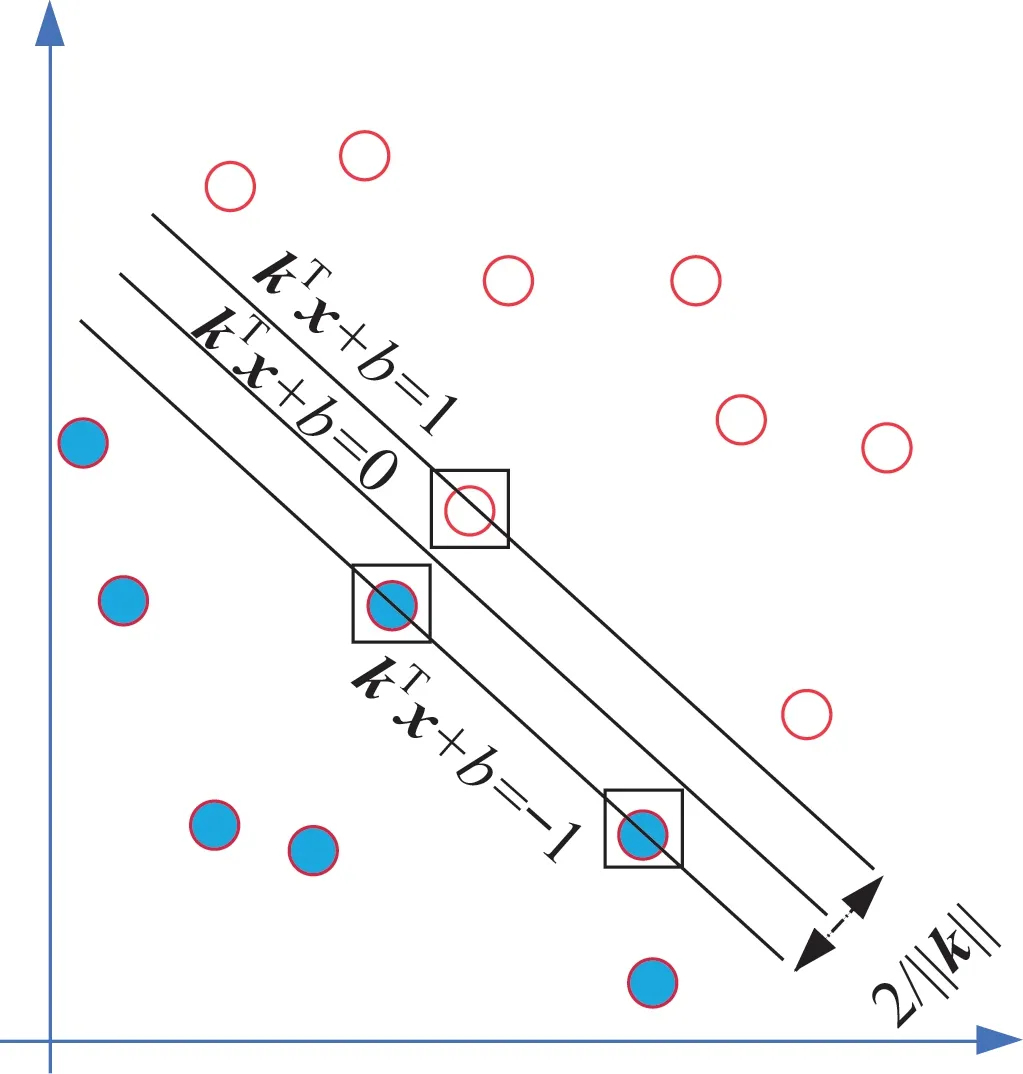
图2 超平面归一化的SVM 分类Fig.2 SVM classification based on hyperplane normalization

由图1 可知，只有距最优分类线较近的几个点起到决定最优分类线位置的作用，这几个点称为支持向量，支持向量位于数据集合的边缘位置，在图2中，被方框圈起来的点即为支持向量。

SVM 可解决二分类和多分类问题，多分类可以由多个二分类SVM 构成，二分类的输出结果为2 个，将输入向量经过多个SVM 判决后，再通过一定的机制裁决，即可得到多分类的输出结果。在二分类SVM 中，假设样本为{xi，yi}(i=1，2，…，n)，xi为输入向量，是样本的特征，yj为输出向量，对于二分类SVM，yj只有2 种结果，n为训练样本的总数。训练SVM 的过程就是寻找1 个超平面，它可以按照其输出向量的要求，将每个样本集划分为2 类，且离超平面最近的2 类间隔最大。

图2 中的kTx+b=0 为归一化后的超平面，平行于此超平面作经过支持向量的超平面，得到kTx+b=1 和kTx+b=-1 两个超平面，分类间隔为，求解超平面的原则是将输入向量划分到要求的输出结果里，且使离超平面最近的2 类的间隔最大，即

式中：k为超平面法向量；xi为输入向量；yj为输出向量；b为常量。

为了方便推导，将式（1）改写为

引入Lagrange 乘子αi≥0(i=1，2，…，n)，得到Lagrange 函数为

式中：αi为Lagrange 乘子。

由于式（3）较难求解，因此将其转化为对偶形式，转化为对偶问题需要满足卡罗需-库恩-塔克（Karush-Kuhn-Tucher，KKT）［12］条件，表达式如下：

式（4）满足KKT 条件后，可将不等式约束转化为等式约束，分别设拉格朗日函数L(k，b，α)对k和b的偏导数为0，表达式如下：

在本章以上的讨论中，认为训练样本线性可分，如讨论线性不可分的问题，则将超平面变为

式中：ϕ(x)为输入变量的映射函数。

令核函数

所以SVM 的最优判决函数为

式（12）为1 个二分类SVM 的判决函数，每1 个输入向量x可得到1 个输出向量。训练SVM 分类器的目的即为了得到1 个判决函数，以便根据训练好的判决函数去分类未知的输入向量［13］。

3 抗干扰决策系统仿真

由表2 可知，抗干扰决策系统需要构造1 个五分类器。从SVM 的理论基础可以看出，多分类器可以由多个二分类器构成。1 个二分类器的输入样本为{xi，yi}，以表2 的前2 行为例，输入向量为两种抗干扰措施中对五种干扰样式的遍历。即对于第1 行采用自适应频率捷变的抗干扰措施时，可以与之对抗的干扰方式为瞄准式干扰、阻塞式干扰和扫频式干扰，假目标干扰以及距离拖引干扰，那么自适应频率捷变可以对抗的干扰方式集合为这4 种干扰，取对抗集合的全部子集作为训练样本的输入向量，再取自适应波形捷变可以对抗的干扰的全部子集为训练样本的输入向量。输出向量为自适应频率捷和自适应波形捷变，值分别为1 和2。可以得到训练样本如图3 所示，这些样本作为1 个二分类SVM 的训练样本，可以将输入向量划分为1 或者2中的某一类。

图3 1 个二分类训练样本Fig.3 A binary training sample

对于表2 所示的问题，需要将五种抗干扰措施两两组合，也就是需要10 个二分类SVM。每种抗干扰措施有其训练样本的集合，通过这些样本的训练即可得到10 个二分类器。因此，要得到1 个输入向量的最优决策结果，就需要将该输入向量分别放入这10 个二分类器中。每个二分类器会得到1 个输出向量，统计10 个二分类器得到的10 个输出向量，将分类结果中出现次数最多的向量，作为这个输入向量的最优决策结果，可得到多分类器的最优结果，该结果即抗干扰决策系统的输出。根据决策结果，雷达可采取该抗干扰措施来对抗当前的干扰信号。

10 组二分类器的训练样本示意如图4 所示，由这10 组训练样本训练得到的10 个二分类器可以对任意1 个输入向量进行五分类。分类的具体方式为：将输入向量分别输入10 个分类器中，得到10 个分类结果，统计这10 个二分类器的结果，将出现次数最多的结果作为最终结果，即需要采取的抗干扰措施。

图4 10 组二分类SVM 器训练样本Fig.4 10 groups of binary SVM training samples

依据以上原理设计抗干扰决策系统，如图5 所示。该系统的操作步骤如下。

图5 抗干扰决策系统仿真结果Fig.5 Simulation results of the anti-jamming decision system

1）根据当前环境中存在的干扰类型和雷达的抗干扰措施对抗效果，运用广义EIF 法评估所有抗干扰手段的抗干扰效果，根据抗干扰效果评估的结果，构造广义EIF 矩阵。

2）对压制式干扰和欺骗式干扰，根据作战的实时需求，分别设置2 个阈值，在广义EIF 矩阵里，将超过阈值的位置置“1”，未超过阈值的位置置“0”。将以0 和1 划分后的广义EIF 矩阵填入抗干扰决策表。如在表中第i行第j列位置元素为1，即认为第j个抗干扰措施可对抗第i个干扰；如为0，则认为第j个抗干扰措施无法对抗第i个干扰。

3）在抗干扰决策系统中输入第2 步得到抗干扰决策表。

4）根据当前环境侦收到的干扰类型，填写输入向量，1 代表当前环境有该类型的干扰，0 代表当前环境没有该类型的干扰。

5）点击运行按钮，得到当前抗干扰系统决策出的最优抗干扰措施。

由图5 的仿真结果可知，抗干扰决策系统可以很好地输入向量进行决策。在实际作战中，抗干扰系统可根据当前环境的干扰类型来决策用哪一种措施。在实际环境中，可运用当前环境侦收到的干扰类型和决策出的抗干扰措施，将评估结果经过处理，填入抗干扰决策系统中，训练基于SVM 的抗干扰决策系统，实时更新抗干扰决策系统。通过不断更新，更好地对当前干扰环境的抗干扰措施作出决策，达到智能化抗干扰系统需要的感知环境，同时实时更新抗干扰措施的目的［14-15］。