运载火箭自适应制导及在线轨迹重构方法研究

汪轶俊，梁艳迁，周 鼎，马振伟，史会涛

（1.上海航天技术研究院，上海 201109；2.上海宇航系统工程研究所，上海 201109；3.中山大学 系统科学与工程学院，广东 广州 510006）

0 引言

作为运载火箭的关键核心子系统，制导系统承担着将有效载荷准确送入预定轨道的任务。在运载火箭“高可靠、高任务适应性和高经济性”的演进目标指引下［1］，伴随行业态势、基础理论、硬件技术、系统架构的快速发展［2-4］，制导方法正经历着计算效率升级与创新突破。

本文回顾运载火箭传统制导方法的发展历程，并立足运载火箭主动适应和自主决策能力的增强需求［5］，讨论分析基于在线轨迹规划的制导方法研究进展。在此基础上，针对运载火箭剩余能量损失导致原目标轨道不可达的问题，提出一种任务降级在线轨迹规划方法，并基于在线轨迹重构开展自适应制导方法的研究。

1 运载火箭制导方法发展历程

1.1 传统制导方法发展历程

运载火箭制导方法的发展一直与硬件条件和基础理论密切相关，导航设备、计算装置的升级，以及控制理论与计算方法的创新持续支撑着制导方法的更新。

在导航设备和计算能力相对不足的条件下，我国早期运载火箭如长征一号配置陀螺和加速度计的捷联导航系统，在模拟计算装置下利用姿态角偏差与视加速度积分反馈的方式控制横法向位置，对关机时间、起飞质量、偏差以及随机干扰形成补偿［6-7］，这种制导方法是基于经典控制理论对特征量偏差的反馈干扰补偿。

为满足远程火箭的发展对导航精度提升的需求，长征二号系列、风暴一号等运载火箭开始采用平台+计算机的制导方案，平台将测量的三个方向视速度增量转换成电脉冲送入计算机依次积分，利用获取的视速度、视位置、视位置积分项进行横法向导引方程计算，通过与装订值的偏差反馈将火箭控制到标准弹道附近，并实现对关机特征量的控制［8-10］，这就是所谓的隐式摄动制导，其在长征三号和长征四号系列运载火箭的早期任务中也得以沿用［11-13］。该方法在当时中等速度、小容量数字增量式箭载计算机条件下能够完成相对高精度的制导［7］。

随着箭载计算机技术的发展，运载火箭的速度、位置等信息可显式地直接计算获取，制导方法也变为显式摄动制导［8］。长征四号和长征二号丁运载火箭先后开始采用全量型数字计算机［14-16］，同时惯性导航开始采用动力调谐陀螺平台［14-16］。在全新的惯性平台和计算设备支撑下，运载火箭制导进入全数字化阶段。

在基于经典控制理论偏差控制的摄动制导日趋完善的前提下，研究的重点开始转向系统冗余和性能优化。硬件方面，长征系列运载火箭逐步开展了平台+激光惯性主从冗余诊断［17］、箭载计算机三CPU 冗余诊断［18］、双八表 捷联惯性主从冗余诊断［19］、单十表捷联惯性诊断［20］等增长可靠性的工作；而理论方法也随着箭载计算机能力的发展开始向最优控制过渡。

由于新任务对运载火箭入轨精度、较大偏差适应性、可靠性等多方面的高要求，基于最优控制理论实时生成最优程序角的迭代制导方法成为当时一种较为合适的工程设计选择［21-22］。迭代制导利用当前实时导航状态与终端入轨约束，计算最优性能弹道，并给出程序角指令，其不需要依赖标称轨迹且实时动态更新，具有较高的制导精度并能适应一定程度的推力下降等偏差。经过10 多年的工程型号应用，迭代制导方法已日臻成熟，并且根据不同的发射任务需求发展出考虑入轨姿态约束、满足多终端约束、跨滑行段、预测修正等多种改进型［23-26］，相关工程应用也正逐步推进。

1.2 基于在线轨迹规划的制导方法概述

近年来，高性能箭载计算机、数值计算理论与方法的快速发展，为运载火箭的制导发展开辟了新的方向，即基于在线轨迹规划进行计算制导与控制［3，27］。尽管迭代制导也是一种最优轨迹控制，但基于线性动力学边值问题解析解的方式使得其无法考虑复杂状态/控制约束，并且需要预先装订终端目标。航天发射任务的高可靠性要求对运载火箭的自主化、智能化和故障适应性提出了更高的要求，典型的场景就是运载火箭发生非致命故障导致剩余能力不足、载荷无法进入原目标轨道时，飞行控制能否实现重构以完成任务救援或减损，而对飞行轨迹和目标轨道进行在线规划重构成为主要的备选方案之一，也是运载火箭制导自适应的主要途径［28］。

2012 年10 月，“德尔塔4”在发射GPS-2F 卫星的过程中发生推力下降，火箭通过在线生成新的飞行轨迹，充分利用剩余推进剂成功完成卫星入轨任务；同月，SpaceX 公司的“猎鹰9”火箭在执行空间站货运补给任务时，一台发动机发生故障而关机，通过任务重构，另外8 台发动机多工作近30 s 以弥补推力损失，成功完成飞船发射［1］。2016 年国际宇航大 会（IAC），俄罗斯专家指出2010 年12 月GLONASS 卫星发射失利中，若及时在线规划基础级与上面级新的交接班条件，上面级利用自身能力仍可将卫星送入预定轨道［5］。进一步表明在线任务重构对提高任务完成率、降低损失的重要性。

在线轨迹规划的主要思路是考虑系统动力学及其他路径约束、任务或阶段终端约束，根据任务需求以某种性能指标最优作为条件，应用先进的问题处理策略及规划算法，实现满足计算速度和计算精度前提下的最优轨迹生成与制导控制指令输出［29］。基于在线轨迹规划制导的关键点为：①规定计算条件下的求解效率；② 算法求解精度；③偏差条件下算法的收敛性，即鲁棒性［30］。当运载火箭发生动力系统故障需要在线轨迹重构（即在线轨迹优化）时，因不存在较为精确的优化初值，且须尽快完成飞行轨迹和制导指令生成，传统制导方法不再适用，故亟须研究鲁棒性强、计算效率高的在线轨迹重构方法以提升任务冗余度与可靠性。据此，国内外从模型约束处理、离散方法、求解算法开发、制导鲁棒性增强等方面开展了相关研究［31-36］。

结合相关研究进展及前期工作［37］，本文最终考虑基于伪谱离散与凸优化理论，提出一种运载火箭故障后剩余能力不足的弹道轨道联合在线重构算法框架，并进行自适应制导方法的研究，为新一代运载火箭的自主化及可靠性增长提供基础支撑和技术途径参考。

2 运载火箭任务降级在线轨迹重构方法

本文主要讨论运载火箭真空飞行段动力系统非致命故障致使有效载荷无法进入原目标轨道的情况，即发生任务降级。这种情况下，基于预先装订标称轨迹或目标轨道的传统制导策略与方法将不再适用，需要火箭能够快速实现飞行弹道及目标轨道的在线规划，进而重构飞行任务及制导以减小非致命故障带来的损失。针对这类任务降级问题，本文基于伪谱离散理论与凸优化方法，提出一种弹道和目标轨道联合在线规划方法，期望开发一套泛化的算法框架适用于某型长征系列运载火箭多种轨道类型任务，实现简洁高效的飞行轨迹重构。

2.1 任务降级规划问题过程约束

任务降级轨迹规划问题可描述为一个动力系统剩余能力、状态及控制路径、终端轨道根数关系约束下3 自由度动力学系统的最优控制问题。对于真空飞行段，系统动力学可通过变量代换构建成一个控制-仿射系统［37］，即

式中：Vx、Vy、Vz和x、y、z分别为原入轨点轨道惯性坐标系（G系，原点位于地心O、y轴指向原入轨点、z轴垂直于轨道面、x轴形成的右手坐标系）下火箭的速度和位置分量；gx、gy、gz为引力加速度分量；T为故障后的发动机推力幅值；m为火箭质量（故障后可根据诊断和参数辨识确定秒耗量，进而确定质量变化规律，无需作为状态变量）；ux、uy、uz为发动机推力方向等效分量，其定义为

式中：ϕ、ψ分别为俯仰角和偏航角。

该等效代换引入一个关于推力方向的附加约束：

相应地，δj（j=x，y，z）为推力方向分量的变化率，其满足：

2.2 终端约束及性能指标

火箭状态正常情况下，载荷入轨的终端约束可表示为状态变量与标称轨道根数之间的强非线性函数关系。然而，在动力系统非致命故障后剩余能力不足时，终端约束难以直接施加，需要构造新的终端约束和性能指标进行任务重构。

任务降级情况下，期望尽可能保证星箭留轨生存，即对轨道近地点提出了下限要求；保证生存的前提下，再考虑重构的新目标轨道与原目标轨道尽可能相似。在该需求下，一种自然的策略是“状态触发”多阶段优化［38］。然而，复杂的优化逻辑分支及强非线性的根数加权指标不利于保证在线计算的收敛性和实时性。考虑对不同任务目标轨道的适应性，并兼顾在线快速求解的可靠性与简洁性，在圆形目标轨道基础上，本文提出一组松弛形式的终端约束为

式中：σh、σq∈R 为松弛变量；wh、wq∈R+为松弛项的惩罚因子；GM 为地球引力常数；xf、yf为终端位置分量；Vxf、Vyf为终端速度分量。

构建上述终端约束和性能指标组合式（5）和式（6），可从物理问题和数值求解两个方面给出解释：物理方面，如果火箭剩余能量足以形成圆形轨道，则松弛变量趋向于零，性能指标退化为圆轨道对应的入轨高度最高；如果剩余能量不足以形成圆轨道，终端约束与性能指标组合即等价于加权优化偏心率和半长轴，通过惩罚项夹逼可形成近圆的椭圆轨道，即形成了一套“能则入圆，否则成椭”的算法框架。数值求解方面，上述松弛-惩罚的约束和指标组合建模形式与序列凸化迭代方法中常用的“虚拟控制”措施相似，在早期迭代中虚拟控制可有效避免由凸化或线性化近似误差引起的“伪不可行”现象，并且随序列迭代下降不致影响最终的收敛解。

综上所述，任务降级轨迹规划的状态变量为x=[Vx，Vy，Vz，x，y，z，ux，uy，uz]T∈R9，控制变量为u=[δx，δy，δz]T∈R3，相应的最优控制问题为

2.3 约束处理与分析

针对式（7）构建的任务降级弹道-轨道联合规划最优控制问题，本节分别对系统动力学、过程约束、终端约束和性能指标函数进行凸化处理，并进行相应的等价性分析。

首先，式（1）描述系统动力学通过变量代换转化成了形如=f(x，t)+B·u的典型控制-仿射系统，序列迭代初始参考轨迹无需控制变量，实现了状态与控制的解耦，利于算法收敛。故式（1）中仅剩引力加速度为非凸项，为保证较长飞行时间过程中的模型精度并兼顾算法的收敛性能，本文采用序列近似方法对引力加速度分量进行凸化处理，即

其次，变量代换引入的推力方向附加约束式（3）可通过无损凸化方法进行松弛，即

这样处理相当于将“球壳”状的非凸可行域凸化为“实心球”状可行域，即二阶锥约束，其等价性可由庞特里亚金极大值原理证明［39］。

最后，关于终端约束式（5）和性能指标式（6）中的非凸项，终端约束只需在终端时刻单点上得到满足，即离散后每个终端约束只有1 维；性能指标无需严格满足，其近似形式与原函数仅需在趋向性或指向性上等价与一致。

所以，本文对上述终端约束和性能指标进行序列线性化近似处理，终端约束式（5）可凸化为

对于性能指标式（6），通过线性化及引入非负辅助变量的方式，将二次指标函数转换为便于凸优化算法求解的线性函数与二阶锥约束的组合，即

式中：σJ为非负辅助变量，通过加权系数wJ进行惩罚。

在序列迭代过程中，当σh、σq和σJ全部收敛至零时，则凸化的性能指标与原指标式（6）同解，可保证降级任务轨道为圆轨道；若最终σh、σq和σJ不为零，说明当前状态和故障条件下的剩余能力无法形成圆轨道，则获得针对原问题的次优解，对应轨道高度与偏心率折中优化尽可能接近圆形的椭圆轨道。即可通过一套算法框架支撑“能则入圆，否则成椭”的在线重构策略。

此外，对上述终端约束和性能指标函数线性化近似处理后，为保证近似的精度和算法的收敛，引入相关变量二阶锥形式的信赖域约束，即

式中：εx、εy、εVx和εVy为信赖域半径。

综上所述，通过无损凸化、序列近似、变量增广及序列线性化措施，任务降级弹道-轨道联合规划问题可以被凸化成用于序列迭代的如下子问题：

进一步，利用Radau 伪谱法对问题式（15）进行离散化处理并排布成如下标准的二阶锥规划（SOCP）形式的子问题：

2.4 在线重构算法设计及数值试验

结合上述讨论，以某型长征系列运载火箭末级推力下降故障为例，本节给出基于伪谱离散和凸优化的任务降级弹道轨道联合在线重构序列迭代算法，见表1。

表1 在线重构算法伪代码Tab.1 Pseudo-code of the online reconstruction algorithm

针对本文涉及的真空段飞行工况，由于动力学系统非线性较弱，序列迭代算法对初始参考轨迹的要求相对较低。为提高算法在线执行的自主性和简便性，所有状态变量在离散点上的初始值设置为标称轨迹在对应秒点上的状态值，由于系统动力学为控制-仿射形式，无需给控制变量赋初值。

为验证算法1 的正确性和快速收敛性能，同时兼顾算法的嵌入式平台移植能力，本节给出任务降级在线重构的数值实验与嵌入式平台性能测试。

数值实验采用标准C 语言，基于Visual Studio 2015 集成开发环境在桌面计算机（Intel-i7-10510U@1.8 GHz，内存16 GB）上进行。对象选取某型运载火箭末子级［37］，原目标轨道为圆形标称轨道，参考轨迹选取末子级飞行标称弹道，伪谱离散配点数为30 个，序列迭代终止的无量纲门限为5×10-4。基于当前算例选取的运载火箭末子级弹道余量，考虑推力故障剩余比例为0.86～1.00，从推力比例为1 开始以0.02 为台阶逐步下调推力确定工况1～工况8，时间零点为三级起飞时刻，考核验证算法对不同故障程度的适应性，以及收敛性能的一致性。不同故障条件下降级重构弹道优化结果在地心发惯系下的分量如图1～图6 所示。

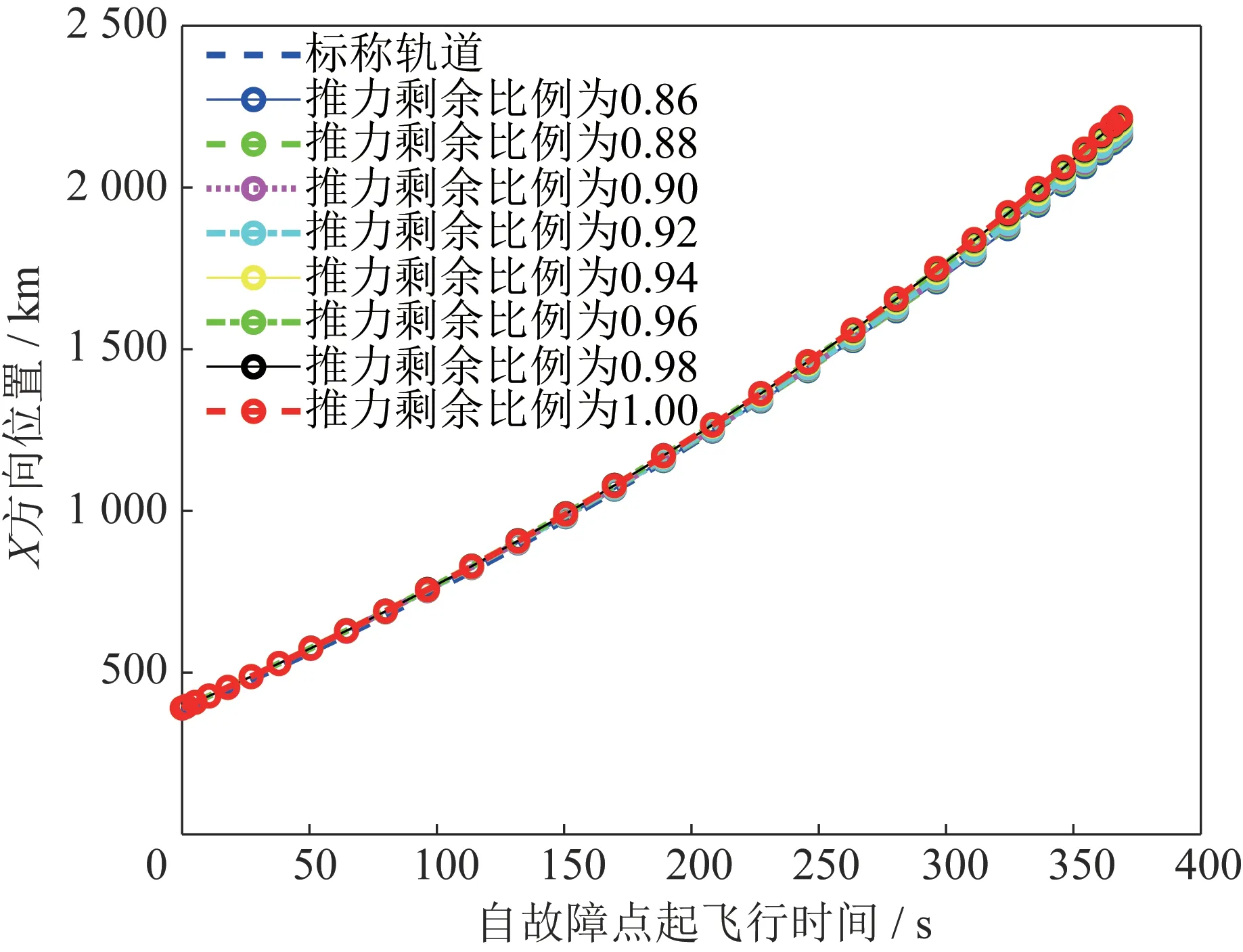
图1 X 方向不同剩余推力比例飞行距离结果对比Fig.1 Comparison of the flight distance results in the Xdirection under different residual thrust ratios

图2 Y 方向不同剩余推力比例飞行距离结果对比Fig.2 Comparison of the flight distance results in the Ydirection under different residual thrust ratios

图3 X 方向不同剩余推力比例飞行速度结果对比Fig.3 Comparison of the flight velocity results in the Xdirection under different residual thrust ratios

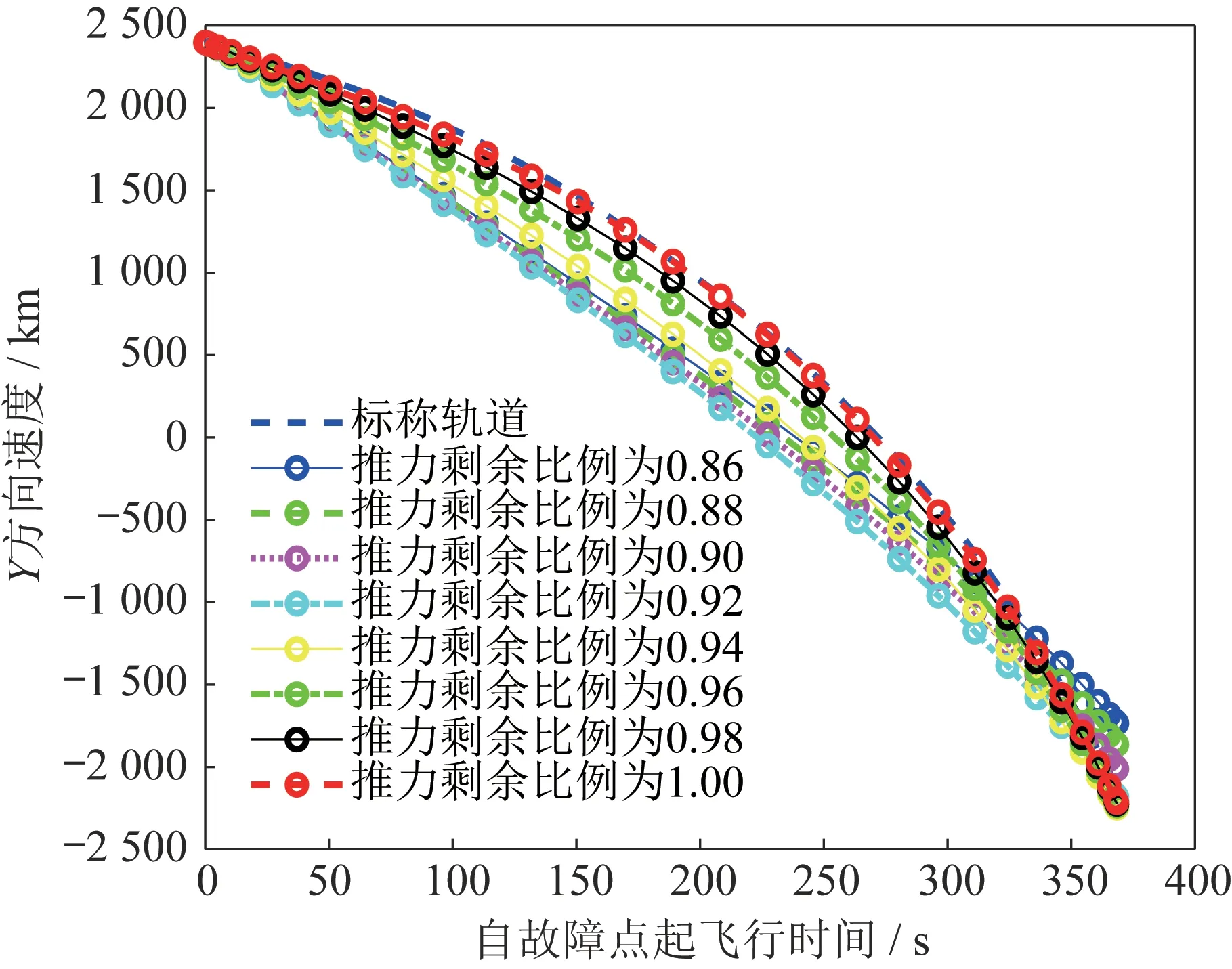
图4 Y 方向不同剩余推力比例飞行速度结果对比Fig.4 Comparison of the flight velocity results in the Ydirection under different residual thrust ratios

图5 不同剩余推力比例下俯仰角结果对比Fig.5 Comparison of the pitch angle results under different residual thrust ratios

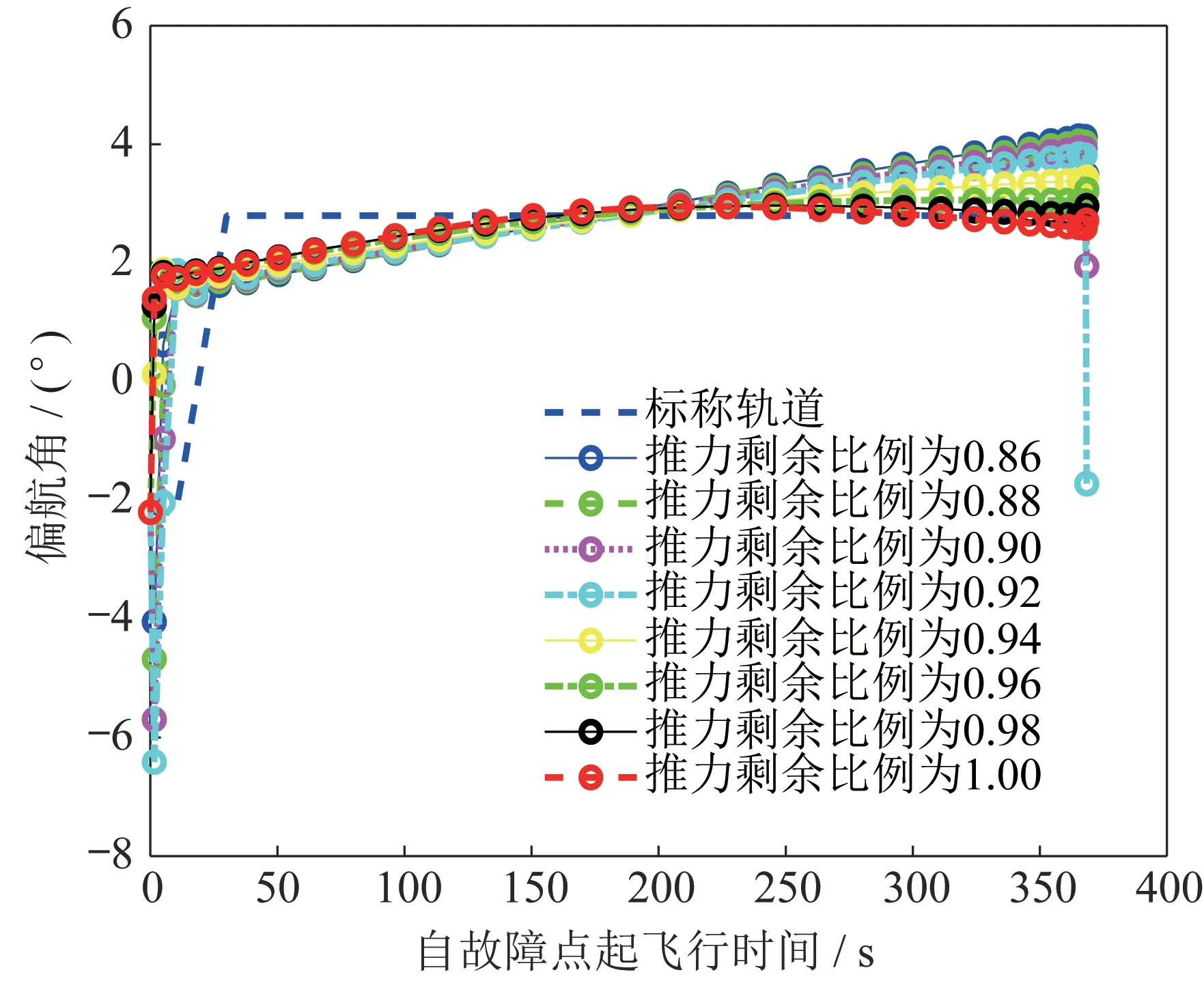
图6 不同剩余推力比例下偏航角结果对比Fig.6 Comparison of the yaw angle results under different residual thrust ratios

相应地，联合重构获得的不同故障条件下所形成的目标轨道如图7 所示，具体轨道根数见表2。由图7 和表1 可知，推力故障下降幅度越大，形成的降级轨道半长轴越低；当推力比例下降到0.86 时，降级轨道近地点已低于地表，物理上已不可行；当前状态下火箭剩余能力足以形成圆轨道时，算法可以得到相应的最高圆轨道，在无法进入圆轨道的情况下，算法也能够给出椭圆重构轨道，且从松弛变量的大小可以发现近地点高度接近最优。这表明，本文的算法对于不同的故障推力工况具有良好的适应性。

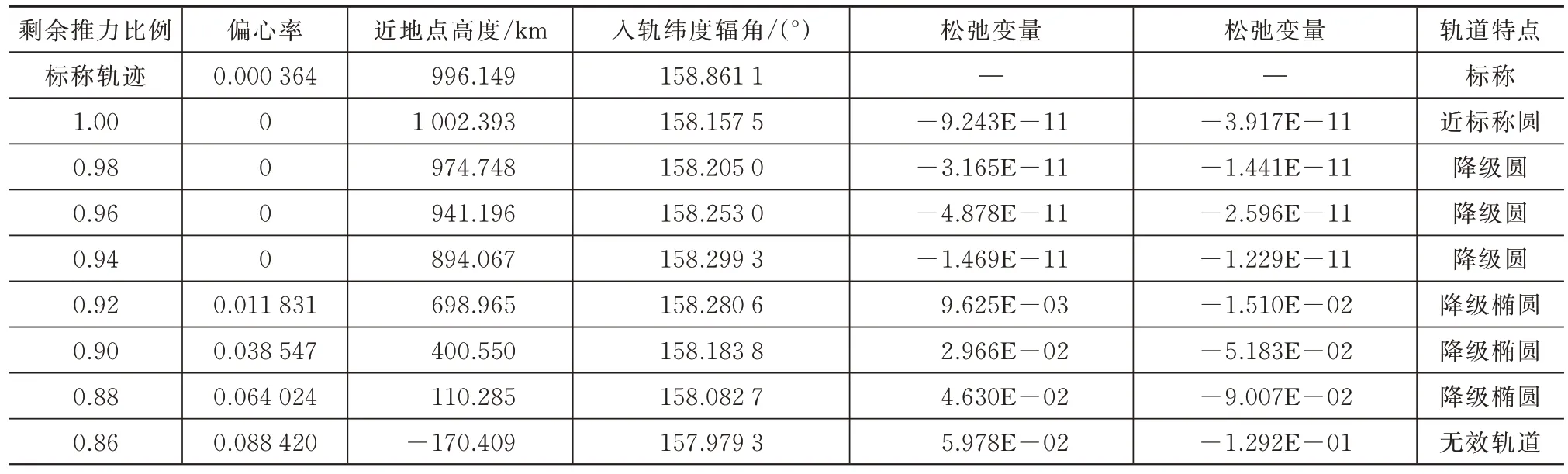
表2 不同剩余推力比例的重构轨道参数Tab.2 Reconfigured orbital parameters of different residual thrust ratios

此外，利用优化获取的控制变量解驱动原始动力学进行积分，并与优化获取的状态变量解进行对比，可量化评估算法的求解精度，位置和速度的最终的积分精度以及序列迭代求解次数与计算耗时，见表3。可以看出，优化的入轨位置精度在0.6 km 以下，速度精度小于2 m/s，算法序列迭代6 次以内可收敛，求解耗时为百毫秒量级且相对稳定。这表明，本文的任务降级在线重构算法具备较高的精度、良好的求解稳定性与快速性，具备在线应用基础。

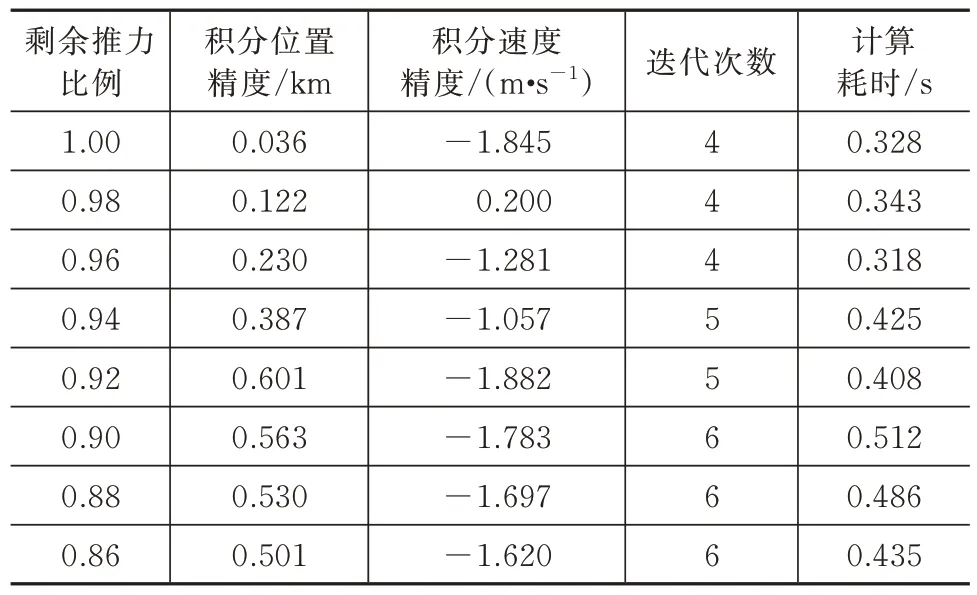
表3 在线重构算法求解精度与性能Tab.3 Accuracy and performance of the online reconfiguration algorithm

为考核本文的任务降级在线轨迹重构算法对不同硬件平台的适应性以支撑未来工程应用，进一步地在x86 架构和ARM 架构的嵌入式计算平台上对算法进行计算耗时与内存占用等性能测试，相关测试结果见表4。可以看出，随着离散配点数的增加，即问题规模扩张，算法的内存占用基本呈线性增加趋势，而计算耗时的增加幅度逐步变大，为后续工程研制提供了改进方向与参考；结合表3，针对同一工况，在精度满足要求的同时，本文的算法在多个嵌入式平台上运行具备1 s 以内收敛的能力，且迭代收敛次数对离散点数选取不敏感，具备良好的跨平台求解稳定性，可以支撑基于在线轨迹重构的自适应制导。

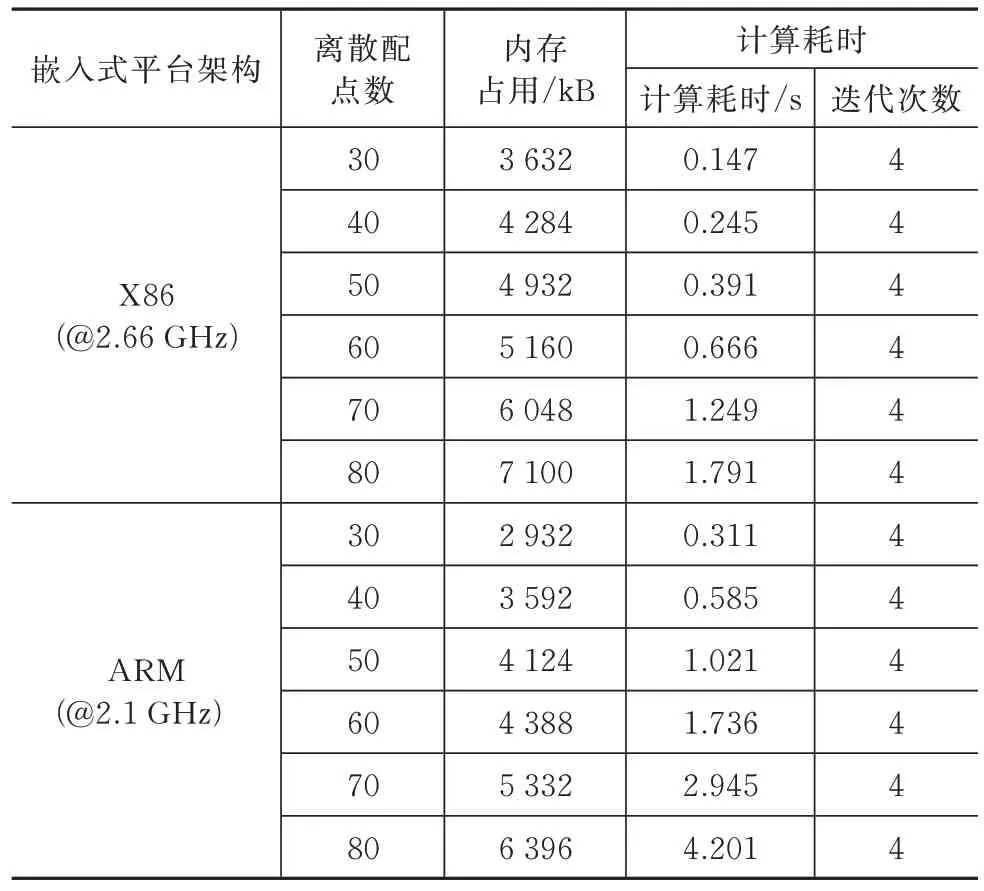
表4 不同硬件平台下性能对比测试Tab.4 Performance tests with different hardware platforms

3 基于在线轨迹重构的自适应制导方法

在线轨迹重构对于制导来说属于基于模型的“一次性”前馈指令，即利用当前触发时刻的系统状态构造最优降级弹道和目标轨道，并生成程序角剖面用于跟踪，或者直接以重构轨道为目标进行迭代制导计算直至到达关机条件。然而，考虑后续飞行过程中可能的故障状态变化，如果模型信息不进行更新，动力学未建模及近似误差、控制系统跟踪误差、故障诊断误差等因素可能会引起制导精度不足乃至优化获取的轨迹最终不可达，这对充分利用实时导航和故障诊断信息的自适应制导提出了需求，即需在线滚动执行轨迹重构并进行误差修正。

3.1 滚动时域自适应制导算法设计

本节以任务降级弹道轨道联合重构的伪谱-序列凸化算法为核心组件，将其嵌入滚动时域框架，基于在线轨迹重构提出一种解决火箭推力故障后任务降级的自适应制导方法。基于在线轨迹重构的自适应制导算法如下。

初始化在线轨迹优化算法所需参数，停止更新终端死区时间［Tbland］；置制导周期索引［i=0］。

步骤1故障注入判断。

如有故障注入，转至步骤2；否则，使用标称轨迹制导指令，转至步骤5。

步骤2故障注入开始最优制导。

在故障注入时刻t0，采集火箭导航信息xR(t0)和故障信息；执行算法1 得到u*(t，xR(t0))，t∈[t0，tf]；在制导周期[t0，t1]内，使用标称轨迹制导指令量应用于系统；置i=1。

步骤3停止滚动时域更新判断。

如果tf-ti≤Tbland，停止滚动时域更新，将u*(t，xR(ti-1))作用于系统直至关机，转至步骤5；否则，转至步骤4。

步骤4滚动时域轨迹优化。

到达制导周期触发时刻ti时，判断第(i-1)次轨迹优化结果是否可用；如可用，将u*(t，xR(ti-1))作用于系统，并采集火箭导航信息xR(ti)和故障信息，执行算法1 得到u*(t，xR(ti))，t∈[ti，tf]；否则，将(i-2)次轨迹优化结果按照时序作用于系统，并采集火箭导航信息xR(ti)和故障信息，执行算法1 得到u*(t，xR(ti))，t∈[ti，tf]。

步骤5关机判断。

如果未达到关机条件，转至步骤1；如果达到关机条件，结束。

注意到，在上述算法的步骤3 中，进行了停止滚动时域轨迹优化更新的判断，即在最后的飞行时间Tbland内，不再进行优化更新计算，在此将Tbland称为“停止更新终端死区时间”。如此设置的目的在于防止在数值优化时域过短的情况下出现计算不稳定、不收敛的情况，防止临近关机时间附近的复杂逻辑判断。同时，在较短的死区Tbland之内，轨迹优化重构带来的性能指标利益已经极小，系统误差和故障检测参数对制导轨迹可行性的影响规模也可忽略。

3.2 数值试验与分析

本节选取与2.4 节相同的对象参数和数值实验环境，设置滚动时域周期为1 s，指令程序角插值步长为0.01 s，仿真动力学模型积分步长为1 ms，停止更新终端死区时间为5 s，通过数值实验对3.1 节算法的基本正确性和有效性进行验证。

首先，在不施加偏差的条件下，通过不同故障时刻-剩余推力比例工况的闭环仿真实验，对比分析单次轨迹重构前馈与滚动时域自适应制导的效果，相关结果见表5。可以发现，在无偏差情况下，单次重构前馈与自适应制导的入轨结果相近。一方面再次验证了单次轨迹重构算法的较高计算精度；另一方面验证了滚动时域自适应制导算法的正确性与有效性。

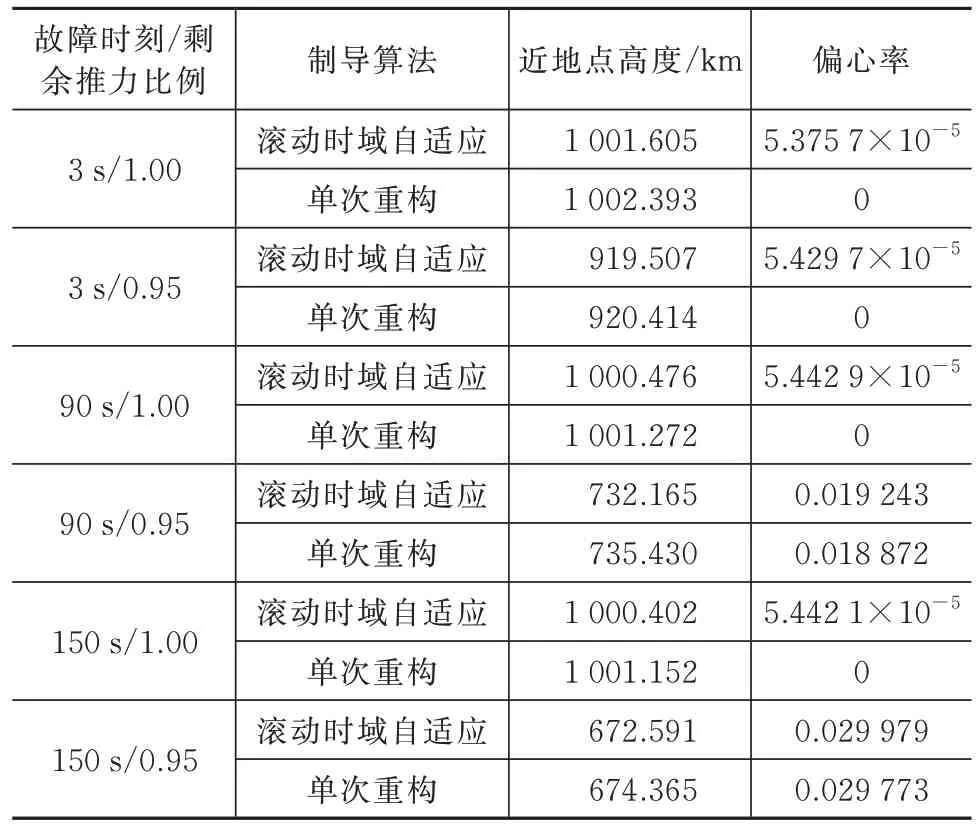
表5 滚动时域自适应制导与单次重构结果对比Tab.5 Comparison of the single reconfiguration and self-adaptive guidance results in the rolling time domain

最后，在闭环仿真的火箭动力学模型中加入推力偏差，而滚动时域制导算法中配置一种推力下降工况，考核基于在线轨迹重构的制导算法对故障诊断结果偏差的适应能力。分别考虑故障发生较早（第3 s）和较晚（第150 s）两种情况，设置推力剩余比例为0.95，分别对动力学模型施加±2%、±3%和±5%的偏差，仿真的入轨结果见表6。结果表明：基于不准确的推力模型，滚动时域最优制导算法仍可以根据火箭实时状态得到最优推力指令，且保持100%的递归可行性。在实际推力施加不同偏差的从小到大变化过程中，优化模型中的推力参数始终不变，入轨近地点高度却随之增大，这一结果充分验证了本文的自适应制导算法利用系统实时状态修正误差的能力，反映了算法对模型失配和外部干扰较好的鲁棒性，也从另一个角度表明动力系统故障诊断精度对制导结果的显著影响。

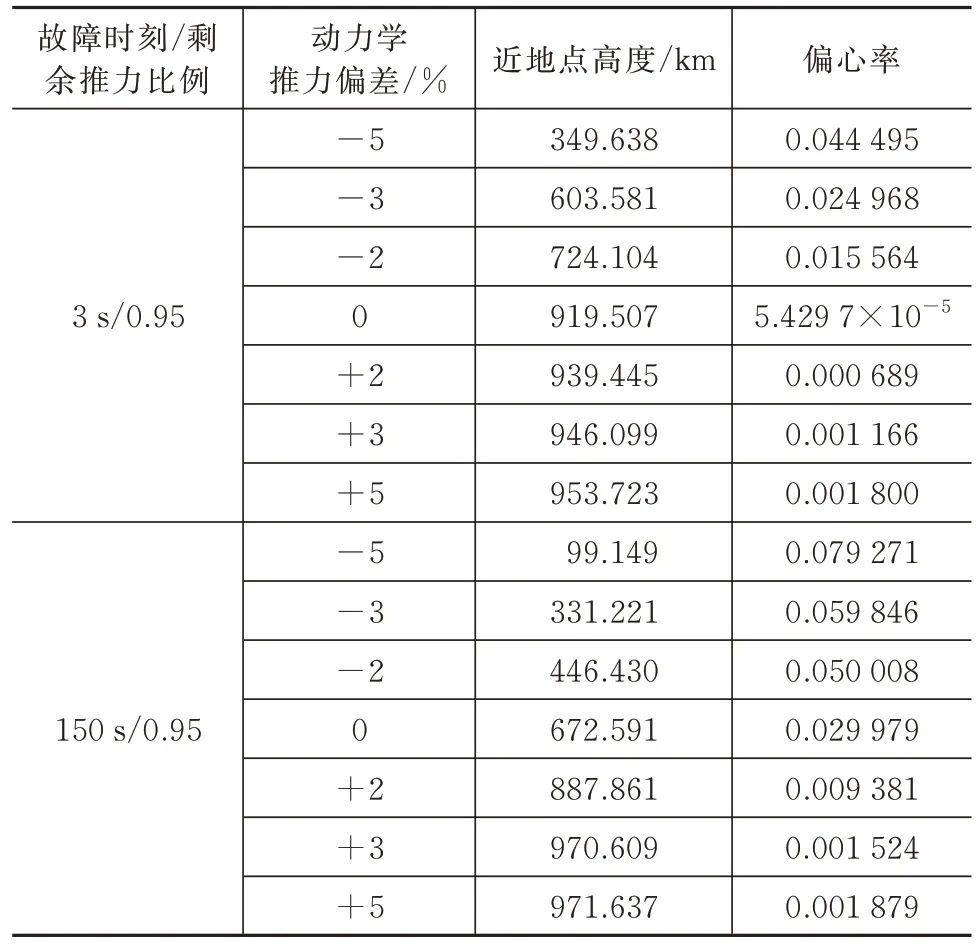
表6 含有推力偏差的滚动时域自适应制导仿真结果Tab.6 Simulation results of the self-adaptive guidance in the rolling time domain with thrust bias

4 结束语

本文从运载火箭的可靠性和适应性提升需求出发，结合我国运载火箭发展历程梳理了工程实践制导方法的发展历程，并基于运载火箭故障冗余任务重构问题，分析了基于在线轨迹规划的制导方法研究进展。立足工程实践，基于伪谱离散和凸优化理论，提出了一种运载火箭任务降级弹道轨道联合在线重构的统一算法框架，据此给出了一种基于滚动时域轨迹重构的自适应制导技术途径，并通过数值实验和嵌入式测试，进行了正确性和有效性验证。本文的研究可为制导技术的更新升级和运载火箭的自主化、智能化发展提供参考依据及基础支撑。