不同深度围压下尾矿砂动力特性研究

2023-03-15王天亮刘松松张胜杰

金属矿山 2023年2期

王林王天亮刘松松张飞张胜杰

(1.道路与铁道工程安全保障省部共建教育部重点实验室,河北石家庄 050043;2.省部共建交通工程结构力学行为与系统安全国家重点实验室,河北石家庄 050043;3.石家庄铁道大学土木工程学院,河北石家庄 050043)

土壤动力特性是指土壤受外部动荷载作用,表现出瞬时结构动态变化的力学性质。与动态荷载相关的机械特性包括动剪切模量、阻尼比、动黏聚力、动内摩擦角等[1],动剪切模量常常表示土壤刚度的动力参数,阻尼比表示了结构受激振后振动的能量衰减[2],动剪切模量和阻尼比的正确评估对抗震结构设计起到重要支撑作用。对动黏聚力和动内摩擦角的变化规律分析显示了岩土工程更小的安全系数和更浅的临界滑动面[3]。对土壤动力特性的研究包含了岩土力学、抗震结构设计、路基工程等多个学科,是土壤强度响应分析和解决各种岩土工程的关键。

尾矿砂作为一种具有高势能的金属矿物废料[4],其主要成分为细沙、粉砂等无黏性土。由于堆积过程中排水不及时,粉细砂处于饱和状态,在地震等动荷载作用下土体内部有效应力降低,容易发生液化现象并造成围挡结构尾矿坝的破坏[5-6]。尾矿砂的处理是国内外研究的热点,尾矿的典型处理方法包括在蓄水过程中以泥浆的形式进行水力沉积,并在自身重力下进行固结[7-8],然而其相对较低的导水率,处理时间相对较长,整治过程中尾矿库需永久保留,并且尾矿砂沉积过程中,土壤颗粒含量等静态指标影响可能不显著[9]。在地震等动荷载作用下,尾矿库的稳定响应受尾矿砂的动力特性影响显著,高强度振动频率下,尾矿砂的剪切强度和刚度可能在孔隙水压力的变化下而降低,从而施加围挡结构尾矿坝更大的水平荷载[10-11]。所以了解尾矿砂动力特性,对评估多种偶然动荷载作用下的尾矿库稳定性能至关重要。

本文介绍了河北某尾矿库尾矿砂动态特性试验研究的结果,分析了不同层次围压下尾矿砂的动态规律,为尾矿库动力安全稳定性技术研究提供基础指标,以评估尾矿库的地震等动荷载作用下的性能分析。

1 试验方案

1.1 试验材料及试样制备

试验材料选用河北某尾矿库内现场不同深度的原状尾矿砂,砂样深度为2.0～24.2 m,砂样基本指标如表1。

表1 不同深度尾矿砂的物理性质Table 1 Physical properties of tailings sand at different depths

1.2 试样制备

将同一深度处的砂样进行烘干、碾碎,按16%含水率配砂,用保鲜膜封闭后静置12 h 以上。三轴试样的尺寸大小选择ϕ39.1 mm×80 mm,通过控制干密度的方式分4 层击实砂样。将制好的试样装入饱和器,先浸没在带有清水注入的真空饱和缸内,连续抽真空抽气6 h,然后停止抽气,静置10 h,最后将饱和后的试样放置于60 ℃的烘箱中烘干至天然含水率后,立即用保鲜膜密封保存。

1.3 试验条件

试验利用静动态三轴实验仪测定不同深度下尾矿砂的动力特性,见图1。试验条件为不固结不排水,动三轴试验采用应力控制方式加载,破坏标准为应变破坏标准,试验结束条件为轴向应变达到5%或循环加载次数达到15 000 次,加载频率为4 Hz,加载波形为正弦波。

图1 冻土静动态三轴实验仪Fig.1 Static dynamic triaxial experimenter of frozen soil

1.4 动强度参数获取原理

1.4.1 动强度曲线

尾矿砂的动强度规律可用动应力σd与达到破坏标准时破坏振次Nf间的关系表示,通过计算机数据采集系统和绘图模块,绘制σd-Nf曲线,利用动强度经验公式σd=a ×(Nf)-b(公式中a、b均为经验参数)对各工况下σd-lgNf关系进行线性拟合,以讨论同一深度下不同围压对尾矿砂动强度曲线发展特性的影响。

1.4.2 动强度指标

根据摩尔—库伦抗剪强度理论:

在σd-Nf曲线上分别截取3 个不同围压作用下与某一破坏振次相对应的动应力σd1、σd2、σd3。对于同一深度的试样,以σc+σd作为大主应力σ1d,以σ3c作为小主应力σ3d,绘制摩尔圆,做出动抗剪强度线,动抗剪强度线的倾角为动内摩擦角φd,动抗剪强度线在纵轴上的截距为动黏聚力cd。

1.4.3 动弹性模量

式中,Ed为动弹性模量,kPa;σd为轴向动应力,kPa;εd为轴向动应变,%。取同一深度中心围压和小动应力幅值的实验结果作为本次试验在此深度处的动弹性模量。

1.4.4 动剪切模量

式中,Gd为动剪切模量,kPa;μ为泊松比;εr为径向应变;εv为体积应变。取同一深度中心围压和小动应力幅值的试验结果作为本次试验在此深度处的动剪切模量。

1.4.5 阻尼比

阻尼比为实际阻尼系数与临界阻尼系数之比,它与对数衰减率和能量损失有关。如图2 所示,1 个周期内的能量损耗近似等于滞回圈ABCD曲线所围定的面积Az(cm2),而1 个周期内的加荷贮存的总能量等于由原点到最大幅值点连线下的三角形OAE的面积As(cm2),故阻尼比λ为

图2 应力应变滞回圈曲线Fig.2 Stress strain hysteresis loop curves

2 试验结果与分析

2.1 不同深度围压下尾矿砂轴向应变特性

连续循环加载作用下,不同深度围压下尾矿砂试样轴向应变时程曲线,如图3 所示。由图3 可见,轴向应变随着循环振次的增加而逐渐累积,并且随着围压的增加,轴向应变积累达到稳定破坏的时间更长,尾矿砂破坏时所表现的轴向应变具有增加的趋势,另外,随着深度围压的增加,尾矿砂破坏时轴向应变的幅值波动较大,累计残余应变更大,土体变形也较为明显。

图3 不同深度围压下尾矿砂轴向应变时程曲线Fig.3 Axial strain time course curves of tailings sand under different depths of confining pressure

2.2 围压对尾矿砂动应力的影响

根据文献[12],将应变标准作为破坏标准,绘制尾矿砂的动强度曲线(σd-Nf曲线),图4 为不同深度下不同围压尾矿砂的动强度曲线。由图4 可见,围压较大时动强度曲线始终位于上方,即尾矿砂随围压的增加,土体动强度值变大。围压用来表征土体的埋深,不同深度下尾矿砂动强度不同,并且随着埋深越大土体动强度越大,这一实验结果与董正方等[13]不同围压下粉砂土动强度变化规律相一致。

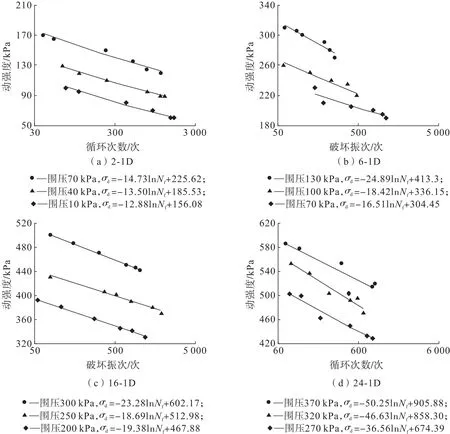
图4 不同深度下尾矿砂动强度曲线Fig.4 Dynamic strength curves of tailings sand at different depths

2.3 不同深度下动强度指标

根据摩尔库伦抗剪强度理论,以σ1d=σc+σd作为大主应力,以σ3d=σ3c为小主应力,绘制摩尔圆,见图5,得到不同深度下2-1D、6-1D、16-1D 及24-1D 尾矿砂动内摩擦角φd和动黏聚力cd。由图5 可见,尾矿砂在2、6、16 及24 m 深度下动内摩擦角为19°、23°、26°和24°,动黏聚力为27.93、37.16、27.93 和27.74 kPa。

图5 不同深度下尾矿砂动抗剪强度线Fig.5 Dynamic shear strength curves of tailings sands at different depths

图6 为尾矿砂动强度指标动内摩擦角随深度变化曲线。由图6 可见,随着深度围压的增加,尾矿砂动内摩擦角出现先增加后减少的趋势,根据试验结果对不同深度下尾矿砂动内摩擦角进行曲线拟合,拟合后曲线关系表达式为y1=-0. 000 1x4+0. 007 2x3-0.191 5x2+2.187 3x+15.156,其中,x表示为尾矿砂深度,y1为动内摩擦角。随着深度的不断增大,尾矿砂压实度逐渐增大,稳定的咬合骨架逐渐形成,摩擦力逐渐增大,进而内摩擦角逐渐增大。随着尾矿砂沉积深度逐渐增大,尾矿砂的沉积状态逐渐趋于稳定,因此其内摩擦角也逐渐趋于稳定。但是随着深度的不断增大,细颗粒尾矿砂逐渐增多,导致粗颗粒尾矿砂之间孔隙被逐渐填满并被包围,并且粗颗粒被细颗粒逐渐托起,致使尾矿砂的稳定咬合结构被破坏,摩擦力逐渐减小,内摩擦角也逐渐减小。

图6 尾矿砂动内摩擦角随深度变化曲线Fig.6 Dynamic friction angle of tailings sand changes curve with depth

图7 为尾矿砂动强度指标动黏聚力随深度变化曲线。由图7 可见,随着沉积深度的逐渐增大,尾矿砂动黏聚力先增大后减少。分析不同深度下尾矿砂动黏聚力变化原因,其在于随着尾矿砂沉积深度的增加,细颗粒含量逐渐增大,由于细颗粒含量逐渐增大,原有粗颗粒的尾矿砂孔隙逐渐被细颗粒的尾矿砂充填,尾矿砂的黏聚力逐渐增大,但是随着细颗粒含量的逐渐增大,粗颗粒逐渐被细颗粒包围,细颗粒的存在增加了尾矿砂的流动性,减小了尾矿砂的咬合力,导致尾矿砂的黏聚力逐渐减小。根据试验结果对不同深度下尾矿砂动黏聚力进行曲线拟合,试验结果满足拟合曲线y2=-0.000 7x4+0.046 1x3-1.110 5x2+9.330 7x+12.886,其中,x为尾矿砂深度,y2为动黏聚力。

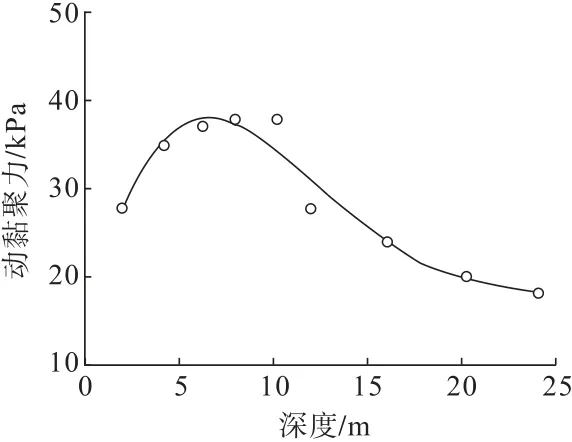
图7 尾矿砂动黏聚力随深度变化曲线Fig.7 Dynamic cohesion curve of tailings sand with depth

2.4 深度对尾矿砂动弹性模量和动剪切模量的影响

图8 为尾矿砂动弹性模量及动剪切模量随深度变化曲线关系。通过对平均动弹性模量随取样深度的变化曲线分析可知,尾矿砂的平均动弹性模量在2.0～ 10.4 m 的范围内时,波动较大,最大值为169.81 MPa,最小值为56.76 MPa。由于尾矿砂的泊松比变化较小,平均动剪切模量的变化趋势与平均动弹性模量的变化趋势相一致。随尾矿砂取样深度的增加,尾矿砂的平均动剪切模量在2.0～10.2 m 的范围内,波动较大,主要分布在56.6 MPa 和18.8 MPa之间,分析其变化较大的原因可能是上部沉积压实度较小,土体中土颗粒容易发生错动,土颗粒之间形成的结构骨架发生改变,在反复动荷载作用下,土体内部能量不均匀,土颗粒间联结不稳定,致使尾矿砂的动剪切模量和动弹性模量出现较大波动。而当尾矿砂大于10.4 m 时,由于受到长期的沉降和固结压实作用,导致尾矿砂的压实度较大,颗粒分布状态稳定。

图8 不同深度对尾矿砂动弹性模量及剪切模量的影响Fig.8 Effects of different depths on the modulus of dynamic elasticity and shear modulus of tailings sands

2.5 不同深度下尾矿砂阻尼比

图9 为尾矿砂阻尼比随深度变化曲线关系。由图9 可见,随着深度的增加,尾矿砂的阻尼比呈现出明显的先减小后增大的变化趋势。随着深度的增大,细粒含量逐渐增大,粗颗粒的尾矿砂孔隙逐渐被填满,应力波在穿越尾矿砂颗粒时所需的能量减小,因此阻尼比逐渐减小。但是随着深度持续增大,含水量的增加,尾矿砂中大量的粗颗粒之间的孔隙之间法向压力增大,在动荷载作用下颗粒间相互摩擦引起的能量耗散增加,因此阻尼比随着深度的升高而增大。