不同加载速率下全尾砂固结体抗拉力学特性研究

程爱平 周成颂 王 平 陈国举 周亚峰

(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.镍钴资源综合利用国家重点实验室,甘肃 金昌 737100)

我国矿产资源种类繁多,性质各异用途广泛,经过一系列复杂的采矿作业和选矿工艺后,在产出有用矿物的同时,也产生了大量的矿山固体废弃物,也就是尾矿。尾矿库的存在不仅造成了土地资源的浪费,而且随着地下深部矿产资源的不断开发,地表沉陷形成塌陷坑,严重破坏和影响地表环境。现阶段,针对采矿作业活动引起的地表塌陷,常用的方法是直接利用矿山固体废弃物对塌陷坑进行回填[1],但是容易造成回填体大规模塌陷、井下泥石流等次生灾害,基于此,利用全尾砂固结回填[2]对矿山塌陷坑进行治理,可以实现真正意义上的“一废治两害”。

塌陷坑全尾砂固结体在井下开采过程中主要受到拉破坏,固结体抗拉强度的大小除了与材料本身的浓度、配比、养护龄期、温度等因素[3-6]有关以外,还与加载速率直接相关,井下爆破扰动、回采速度等都会影响固结体的受载速率,如何保证开采过程中塌陷坑全尾砂固结体的稳定性至关重要。目前,许多学者对加载速率影响下的岩石及类岩石材料的抗压强度特性开展了广泛研究,李福林等[7]对泥岩的单轴抗压强度特性及蠕变变形进行了加载速率效应研究,得出加载速率与蠕变变形量关系呈正相关;侯永强等[8]开展了5 种不同加载速率下的充填体单轴压缩实验,探讨了不同加载速率下充填体的能耗演化过程,发现充填体的强度存在临界加载速率现象;Cao 等[9]研究了固化180 d 的充填体抗压强度和声发射特性,结果表明加载速率对充填体的长期强度具有强化效应;Fischer 等[10]研究得出了在应力速率为0.01～100 MPa/s 的准静态状态下,2 d 养护龄期的水泥浆体抗压强度随加载速率的增加而增加的规律;唐一举等[11]对煤岩材料单轴压缩条件下的破坏特征进行了加载速率效应研究,试验结果显示试样破坏形态与能量演化均与加载速率密切相关;王云飞等[12]分别对干燥和饱水状态下的砂岩进行了不同加载速率下的单轴压缩试验,研究发现随加载速率的增加,拉伸破坏裂隙所占百分比增加;Ma Qing 等[13]对煤岩复合材料进行了加载速率效应研究,研究结果表明煤岩复合材料的强度、变形、声发射(AE)和能量演化均具有一定的加载速率效应。

上述研究表明加载速率对岩石及类岩石材料的抗压强度特性影响较大。也有少量的学者对岩石及类岩石材料抗拉强度的加载速率效应开展了相关研究[14-18],但对处于开采活动过程中的塌陷坑全尾砂固结体,这一特殊工况下低强度材料抗拉强度特性的加载速率效应研究较少。

基于此,本文制作不同浓度及配比的全尾砂固结体试样,开展不同加载速率下的抗拉试验,探讨不同加载速率下固结体抗拉强度、变形、破坏模式及能量演化特征,揭示加载速率对固结体抗拉破坏的影响机理,为保障矿山安全开采提供指导意见。

1 试验设计

1.1 试验原料

全尾砂固结体抗拉试验所用尾砂均取自程潮铁矿尾矿库,尾砂的选取采用以尾矿库尾矿流出口向库内中心的延伸线为轴线,沿途每隔相同距离共选取6个点,并从所选点获取试验所需全尾砂的方法[19]。尾砂颗粒粒径组成如图1 所示,不均匀系数5.62,曲率系数1.25。采用32.5#普通硅酸盐水泥作为胶结材料,试验用水为试验室内自来水。

图1 全尾砂颗粒粒径组成Fig.1 Particle size composition of full tailings

1.2 试验原理

为了研究不同加载速率下全尾砂固结体的抗拉强度特性,试验参照《GBT 50081—2019 混凝土物理力学性能试验方法标准》,制作出抗拉试验所需的2 块横截面半径为75 mm、长100 mm、宽100 mm、厚20 mm 的钢制弧形垫块,以及长度为100 mm,宽度为20 mm,厚度为3 mm 的木质垫条,结合WDW-100kN型微机电子万能试验机对固结体进行抗拉试验,间接测得其抗拉强度。抗拉试验原理见图2。

图2 抗拉试验原理图Fig.2 Schematic diagram of tensile test

如图2 所示,利用弧形钢制垫块给方形试样沿中轴线施加径向的线荷载,试样在压缩线荷载作用下沿着垂直于径向加载方向的水平方向产生拉应力,直至试样发生破坏。由于全尾砂固结体的强度较低,垫条的存在是为了避免提供线荷载的垫块与试样直接接触,产生局部破坏,进而影响试验结果。根据《GBT 50081—2019 混凝土物理力学性能试验方法标准》,全尾砂固结体抗拉强度按下式进行计算:

式中,fts为固结体劈裂抗拉强度,MPa(对于试样尺寸为100 mm×100 mm×100 mm 的方形试样,算得抗拉强度值应乘以尺寸换算系数0.85);F为试样破坏荷载,N;A为试样劈裂面面积,mm2。

1.3 试验方案

本次试验设计制作3 种不同配比(1 ∶4、1 ∶6、1 ∶8)和不同浓度(68%、72%、76%)的全尾砂固结体试样,设计采用5 种不同的加载速率(0.01、0.02、0.05、0.1、0.2 kN/s)进行加载。为了减少试验误差,同一加载速率、浓度、灰砂比制作3 个试样,总计54 个试样。试样命名方式为L(M、H)-4(6、8)-1(2、3、4、5),L、M、H 分别代表浓度68%、72%、76%,4、6、8 分别代表灰砂比1 ∶4、1 ∶6、1 ∶8,1、2、3、4、5 分别代表加载速率0.01、0.02、0.05、0.1、0.2 kN/s。例如H-6-2,即为浓度为76%,灰砂比为1 ∶6,加载速率为0.02 kN/s 的试样。

根据《GBT 50081—2019 混凝土物理力学性能试验方法标准》,配置9 种全尾砂固结体料浆,料浆通过漏斗浇筑到方形钢制模具中,充分振荡,最终制作成尺寸为100 mm×100 mm×100 mm 的方形试样。试样放置于养护环境为温度20±0.5 ℃,相对湿度为96%的标准养护箱内养护,养护龄期为28 d。在试验开始前,对试样表面进行处理,用502 胶水将垫条粘贴固定在试样的上下面中心处,然后将试样放在试验机下承压板的中心位置,在试样与上下压板之间放置弧形钢制垫块各1 块,垫块应与试样上下面的中心线对准;启动试验机,使试样与加载台接触,采用应力控制模式加载,试验流程见图3。

图3 试验流程Fig.3 Test flow chart

2 试验结果

图4 为5 种不同加载速率下不同配比不同浓度全尾砂固结体试样的应力应变曲线图。由图4 可知,随着配比及浓度的提升,全尾砂固结体试样抗拉强度逐渐增大,抗拉强度最低的为浓度68%、灰砂比1 ∶8的6 个试样,均低于0.1 MPa,抗拉强度最高的为浓度76%、灰砂比1 ∶4 的6 个试样,在0.33～0.4MPa之间;灰砂比为1 ∶8 和1 ∶6 的全尾砂固结体整体强度都很小,浓度的变化对其抗拉强度影响并不大,随着加载速率的增大,其抗拉强度整体有增大的趋势,灰砂比为1 ∶4 的固结体抗拉强度明显受浓度影响较大;不同的加载速率下固结体试样抗拉强度不同,低浓度低配比的固结体试样抗拉强度受加载速率影响波动 较大。

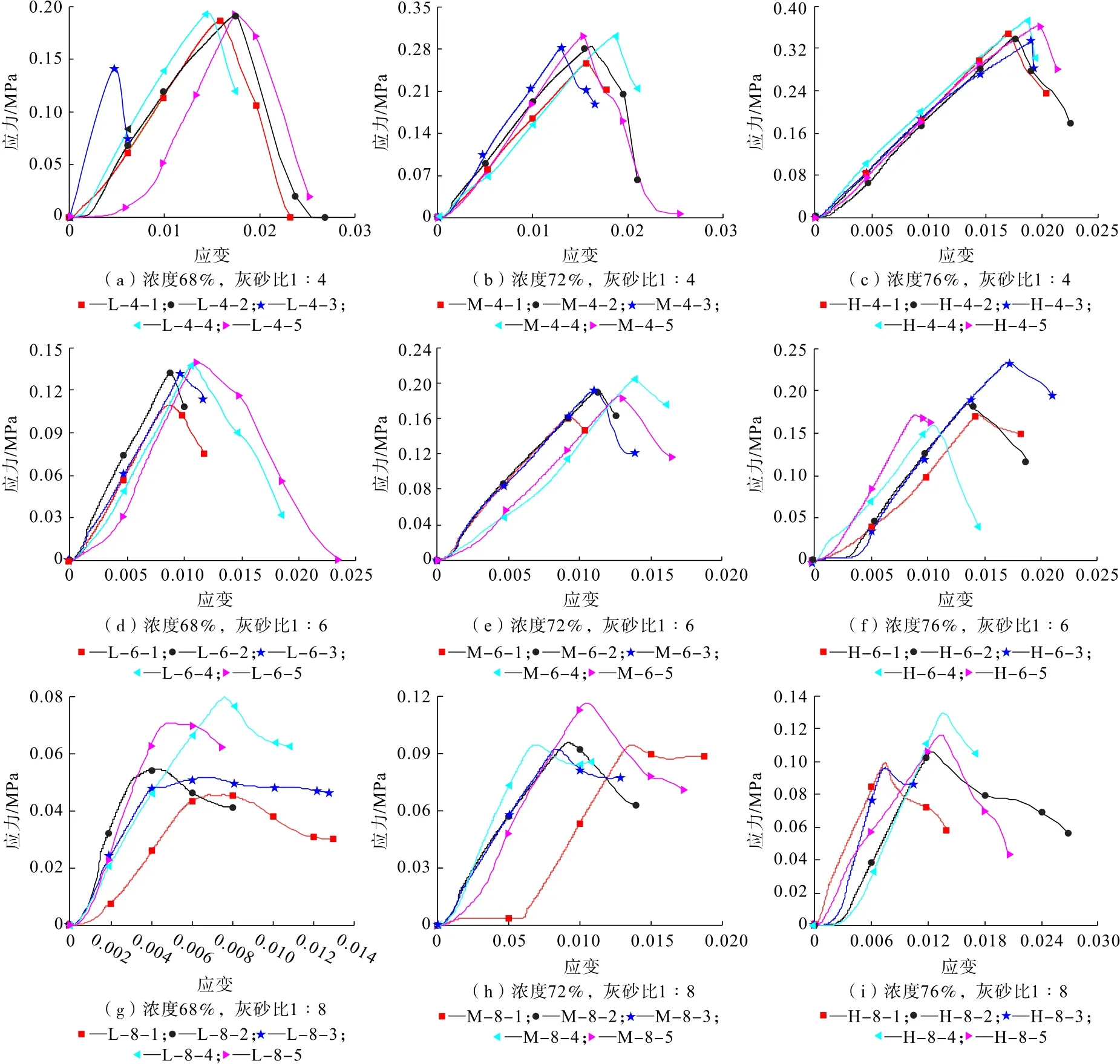
图4 不同加载速率下全尾砂固结体抗拉强度压应力应变曲线 Fig.4 The compressive stress-strain curves of the tensile strength of full tailings consolidation under different loading rates

3 讨论

3.1 不同加载速率下固结体试样抗拉强度与变形特征

图5 为5 种不同加载速率下不同配比不同浓度全尾砂固结体试样的强度变化曲线图,本文以灰砂比为1 ∶4,浓度为76%的固结体试样为例进行分析。当加载速率为0.01 kN/s 时,固结体抗拉强度较高,这是由于固结体为人工制作的含不同粒径的骨料、胶凝材料以及水混合而成的非均质材料,固结体内部含有大量孔隙和裂隙,低速率加载对固结体内部的原始孔隙存在压密效应,减少了试样内部的孔隙裂隙数量,略微提高了固结体的抗拉强度。当加载速率为0.02 kN/s 时,固结体抗拉强度降低,此时压密效应减弱,部分孔隙和裂隙得到了充分的发育。当加载速率为0.05 kN/s 时,固结体抗拉强度降为最低,此时压密效应完全消失,固结体内部的裂隙得到了充分的发育。当加载速率为0.1 kN/s 时,固结体抗拉强度值大幅增加,此时固结体破裂演化时间大幅度减少,对孔隙发育存在抑制效应。当加载速率为0.2 kN/s时,固结体抗拉强度略微降低,孔隙发育抑制效应趋于稳定。

图5 固结体抗拉强度与加载速率的关系Fig.5 The relationship between tensile strength and loading rate of consolidation

综上可以看出,随加载速率的不断提高,固结体抗拉强度整体呈现先减小后增加最后趋于稳定的规律性。将强度转折点定为临界加载速率[20],因此,本次试验存在双临界加载速率,分别是第一临界加载速率0.05 kN/s,第二临界加载速率0.1 kN/s。

通常情况下,应力应变曲线斜率接近稳定的阶段即为弹性变形阶段,材料抵抗弹性变形能力的大小称为弹性模量,单位为MPa;将峰值应力点与原点间的割线斜率定义为变形模量,单位为MPa。图6 给出的是不同加载速率下弹性模量与变形模量变化图。由图6 可知,固结体弹性模量和变形模量随加载速率的变化规律与固结体的抗拉强度基本保持一致。在0.05 kN/s 的第一临界加载速率下,固结体的弹性模量与变形模量达到最小值,说明此时固结体抵抗变形的能力最弱。在0.1 kN/s 的第二临界加载速率下,固结体的弹性模量与变形模量达到最大值,说明此时固结体抵抗变形的能力最强。

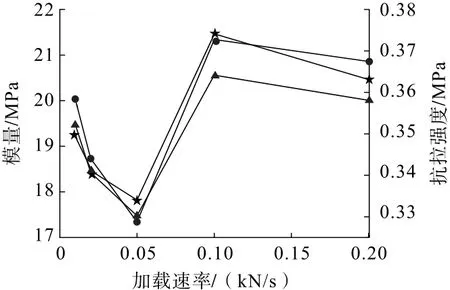
图6 不同加载速率下固结体弹性模量与变形模量变化Fig.6 Changes of elastic modulus and deformation modulus of consolidation under different loading rates

3.2 不同加载速率下固结体破坏模式

不同加载速率下的固结体最终破坏模式如图7所示,固结体试样整体主要破坏模式为拉伸破坏。

图7 不同加载速率下固结体破坏模式Fig.7 Failure modes of consolidated body under different loading rates

进一步对图7 进行分析可以得出:当加载速率为0.01 kN/s 时,固结体试样沿着加载方向形成1 条上下贯通的主裂缝,并在上端部产生了1 条较短的次生裂缝,裂纹总条数为2 条。由于低速率的压密效应,使固结体内部的大量微孔隙闭合,在一定程度上抑制了裂纹数量的产生。当加载速率为0.02 kN/s 时,固结体中心产生上下贯通的主裂纹的同时,在右下方产生了1 条较长的次生裂缝,总裂纹条数为2 条,表明随着加载速率的提高,压密效应减弱,固结体内部微裂隙更易扩展成裂纹。当加载速率增加到第一临界加载速率0.05 kN/s 时,在试样中心沿着加载方向产生了2 条相互交错的主裂纹,同时在这2 条裂纹的左上方和右下方各产生了1 条较短的次生裂缝,裂纹总条数为4 条,表明低速率的压密效应完全消失,固结体内部裂隙得到了充分发育。当加载速率增加到第二临界加载速率0.1 kN/s 时,固结体试样沿着加载方向产生1 条上下贯通的主裂纹,同时在试样中部位置沿水平方向产生了次生裂缝,裂纹总条数最少,为2 条。0.2 kN/s 的高加载速率左右两边各产生1 条次生裂缝,总裂纹条数为3 条,表明高加载速率对固结体内部孔隙发育存在抑制效应。

3.3 不同加载速率下固结体能量演化特征

对应力应变曲线进行积分,即可得出外部荷载输入的总应变能。能量演化方程[21]如下:

式中,W表示外部的荷载所输入的总应变能;We和Wd分别表示应变过程中储存在岩石内的弹性应变能和岩石破碎时的耗散能。W、We和Wd的单位均为kJ/m3,弹性应变能的计算公式可简化为

其中E为初始弹性模量。定义耗散能与弹性应变能在某一时刻的比值为耗弹比λ,计算公式为

式中,Wid和Wie分别表示应变过程中第i时刻岩石破碎时的耗散能和储存在岩石内的弹性应变能。

本文以浓度为76%、灰砂比为1 ∶4 的全尾砂固结体试样为例,探讨不同加载速率下的全尾砂固结体能量演化规律。由图8 可知,在0.01 kN/s 低速率加载下(图8(a)),固结体的弹性应变能增加缓慢,耗散能增长迅速,这是由于低速率作用下,试验机对固结体做的功中很大一部分用于固结体内部孔隙的压密与发育,导致用于抵抗固结体整体变形的弹性应变能较小,试样破坏缓慢。在0.05 kN/s 的第一临界加载速率下(图8(c)),当弹性应变能达到峰值点后近乎垂直下降,与此同时耗散能垂直上升,表明此刻试样发生了剧烈破坏,弹性应变能迅速被释放,这与图7中固结体试样在0.05 kN/s 加载速率下的破坏模式相一致。在0.1 kN/s 的第二临界加载速率下(图8(d)),固结体弹性应变能增长较快,耗散能的增长明显被削弱,这是由于在较高速率的作用下,固结体内部孔隙来不及发育就迅速被破坏,弹性应变能的作用发挥到了最大化,此时固结体强度达到最大。

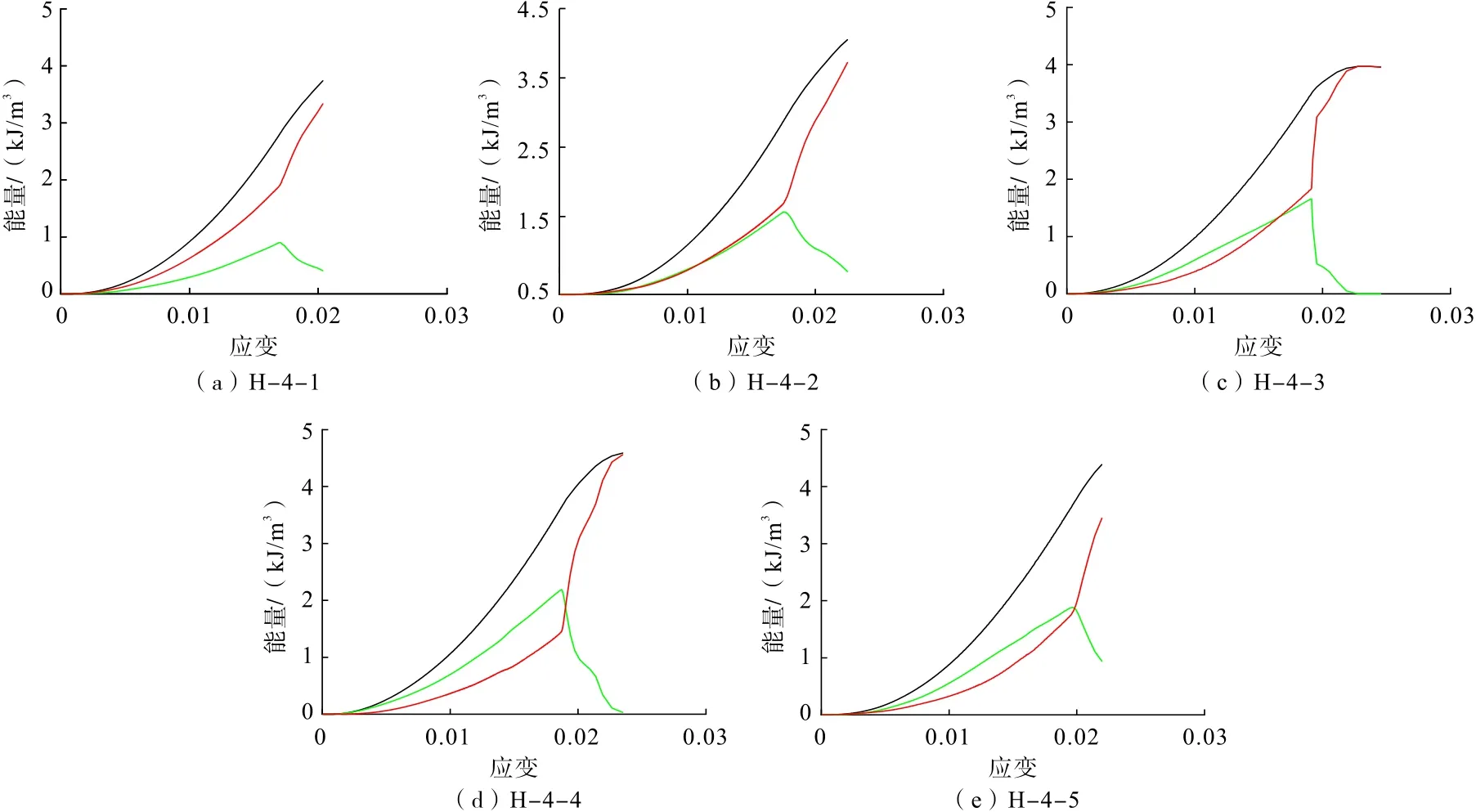
图8 不同加载速率下固结体能量演化过程Fig.8 Energy evolution and dissipation coefficient of consolidated samples under different loading rates

为表征不同加载速率下全尾砂固结体能量耗散规律,将总应变能分为峰前应变能和峰后应变能(如图9 所示),定义全尾砂固结体在破坏过程中某一时刻的耗散能与弹性应变能的比值为耗弹比,分别获得峰值耗弹比与最终耗弹比(如图10 所示)。

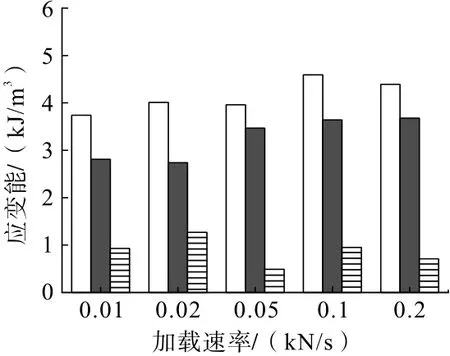
图9 应变能随加载速率变化Fig.9 Strain energy variation with loading rate

由图9 可知,随加载速率的增加,固结体的总应变能及峰前应变能都有整体提升的趋势,0.01～0.2 kN/s 加载速率对应总应变能分别达到了3.74、4.04、3.96、4.59、4.39 kJ/m3,对应的峰前应变能分别占比为75.14%、68.33%、87.63%、79.30%、83.83%,即峰后应变能对应占比为24.86%、31.67%、12.37%、20.70%、16.17%;在0.05 kN/s 的第一临界加载速率下,固结体的峰后应变能占比最低,在0.1 kN/s 的第二临界加载速率下,固结体的总应变能最高。由图10 可知,最终耗弹比先增大后减小,当加载速率为0.05 kN/s 时,最终耗弹比达到最大;峰值耗弹比先减小后增大,当加载速率为0.1 kN/s 时,峰值耗弹比达到最小。

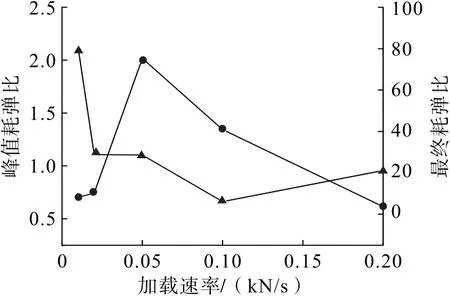
图10 耗弹比随加载速率变化Fig.10 Ratio of dissipated energy to elastic strain energy changing with loading rate

4 结论

(1)低加载速率下,全尾砂固结体原始孔隙存在压密效应,随着加载速率的增加,压密效应逐渐消失。当加载速率为0.05 kN/s 时,全尾砂固结体抗拉强度最低。高加载速率下,全尾砂固结体孔隙发育存在抑制效应,随着加载速率的增加,抑制效应先增大后减小,当加载速率为0.1 kN/s 时,全尾砂固结体抗拉强度最高。全尾砂固结体弹性模量及变形模量的变化趋势与抗拉强度一致。

(2)不同加载速率下,全尾砂固结体宏观破坏模式均为拉伸破坏,裂纹数量随加载速率变化显著。当加载速率低于0.05 kN/s 时,随着加载速率的增加,固结体次生裂纹条数逐渐增加,破坏愈加明显,在0.05 kN/s 时其裂纹条数达到峰值,同时破坏最为剧烈,说明此时固结体抵抗变形的能力最弱。0.1 kN/s加载速率下,固结体破坏较为迅速,破坏面完整,次生裂缝较少。

(3)当加载速率低于0.05 kN/s 时,随着加载速率的增加,固结体弹性应变能增长缓慢,能量耗散较快。当加载速率为0.05 kN/s 时,峰前应变能占比最高,峰后应变能占比最低,最终耗弹比最大。当加载速率高于0.05 kN/s 时,固结体弹性应变能增长较快,能量耗散较缓。当加载速率为0.1 kN/s 时,固结体总应变能最大,峰值耗弹比最小。

(4)全尾砂固结体抗拉强度特性存在明显的加载速率效应,具有双临界加载速率:第一临界加载速率(0.05 kN/s)作用下,固结体抵抗变形的能力较弱,整体抗拉特性较差;第二临界加载速率(0.1 kN/s)作用下,固结体抵抗变形的能力较强,整体抗拉特性较好。