GNSS-R潮位监测抗差估计

王泽明，李浩军，孙亚峰

1.同济大学测绘与地理信息学院，上海 200092；2.上海市城市建设设计研究总院(集团)有限公司，上海 200125

临海国家的生产生活受海平面升降影响巨大，因此对海平面进行实时监测向来是众多研究领域的重点[1]。监测海平面高度变化的传统方法主要包括验潮站实测与激光测高技术。作为观测精度最高的验潮站数据，仍然存在着地理分布不均和数据不公开等问题。具有良好测高能力的激光测高技术在近岸地区的水位监测方面存在着精度低和卫星重访问周期长等问题[2]。全球导航卫星系统反射技术(global navigation satellite system reflectometry，GNSS-R)是一种基于GNSS反射信号的全新遥感技术，它通过分析反射信号的波形、振幅、相位、频率等信息，提取出隐含在其中的反射面的物理特性[3]。该技术的优势在于反射点具有密集的空间分布，可以覆盖测站周围整个区域，且接收机天线距反射面高度越高，覆盖范围越大，因而不再局限于诸如浮标、验潮站等单一测量点的测量模式[4]。与传统遥感测量技术相比，GNSS-R技术不需要专门的雷达发射机，并且具有全天候、覆盖范围广、时间分辨率高、成本低等优点[5]，目前已应用于地表土壤湿度、植被变化、海面风速、雪深和潮位等的反演[6-11]。

目前，GNSS-R技术在水面高度反演领域已经取得众多成果。文献[12]在Crater湖上开展的基于1 Hz采样率的试验获得了2 cm精度的水面高度。文献[13]设计了一款基于GNSS反射信号的潮汐计量仪，在Onsala空间天文台展开的试验获得了4 cm精度的水面高度。文献[14]基于机载GNSS-R技术，对已有反演模型进行优化，获得了5 cm高程精度和5 km空间分辨率。文献[15]对信噪比序列和频谱分析阈值进行约束，基于最小二乘方法，结合多个GNSS星座，对时间跨度为3个月的数据进行潮位反演，试验所得相关系数高达0.97，同时指出GNSS-R技术在反演海面高度方面有很强的实用价值。文献[16]提出一种圆周回归估计算法和一种接收机体系结构，试验所得海面高度反演精度为厘米级。

针对验潮站参考面至天线相位中心间垂直距离(下文简称“测站高”)的求解，以往绝大多数研究采用对应历元水面高度与潮位取平均的方法，本文提出了基于抗差估计的优化方法，采用4个IGS GNSS连续运行跟踪站HNLC、SC02、TDAM、TPW2的观测数据进行数据处理。结果表明，本文方法对水面高度粗差反演值的剔除、测站高计算精度的提升，以及对最终反演潮位结果都具有重要的意义。同时，验证了基于先验潮位数据求得的测站高用于后续无验潮站或验潮站数据中断情况下的GNSS-R潮位反演的可行性。

1 精准测站高计算原理

1.1 SNR反演水面高度原理

信噪比(signal noise ratio，SNR)是GNSS接收机观测数据中信号与噪声的比例，由卫星直射、反射信号叠加干涉形成。可由式(1)计算得出[17]

(1)

式中，Ad表示直射信号的振幅；Am表示由多路径效应引起的局部周期性变化[18]；Ψ表示直反射信号间的相位差。因反射信号对GNSS定位精度造成严重影响，通常被接收机天线的扼流圈和天线增益所抑制[19]，且反射信号在被反射时会发生能量衰减，故直射信号与反射信号的振幅满足Ad≫Am的关系[18]，因此式(1)可近似为

(2)

式(2)表明，直射信号构成了SNR的主体，表征着整体变化趋势；而反射信号对SNR的贡献体现在小幅度的周期性震荡扰动，且该扰动仅在低卫星高度角时较为显著[20]。

相位差的产生源于直反射信号之间存在路径延迟，二者间的关系可表示为[21-22]

(3)

式中，λ表示卫星信号的载波波长；δ表示直反射信号的路径延迟。如图1所示，路径延迟δ可表示为

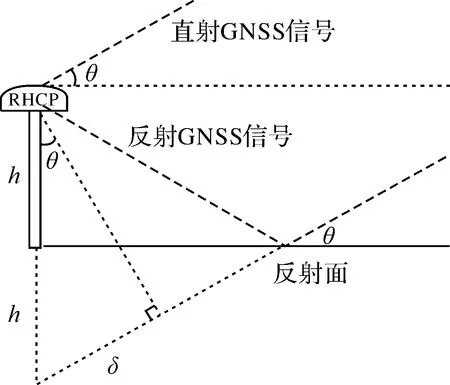
图1 GNSS-R反演模型

δ=2hsinθ

(4)

式中，h表示自反射面起算的接收机天线相位中心的高度；θ为卫星高度角。

根据式(3)、式(4)，对相位差Ψ求时间的导数，可获得多路径效应振荡频率为[15]

(5)

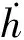
(6)

(7)

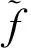
由于LSP分析提取的是水面高度，故在与验潮站实测数据对比分析前，需要进行如下转换[19,26]

htide(t)=[h(t0)+Htide(t0)]-h(t)

(8)

式中，htide(t)为t时刻反演所得潮位高度；h(t0)为某一参考时刻t0反演所得水面高度；Htide(t0)为t0时刻验潮站实测潮位；h(t)为t时刻反演所得水面高度。可以看出，h(t0)+Htide(t0)表示的正是基于验潮站参考基准起算的测站高。对于该高度的求取，多数研究将试验期间所有反演结果取均值代入h(t0)，并将与反演结果对应时刻的实际潮位高度取均值代入Htide(t0)，计算得测站高。由于GNSS-R技术反演水面高度利用的是水面反射的卫星信号，而测站周围的建筑、植被、行船等地物同样会将部分卫星信号反射传入接收机；此外，大气折射效应会使卫星信号发生弯曲，从而导致计算高度角与实际高度角不同，引起潮位反演结果的偏差[27]；海面粗糙度大时，高频海浪会导致绝大部分反射信号来自波峰，低频海浪会导致绝大部分反射信号来自波谷，导致获取的水面高度并非是基于平均海平面起算的水面高度[15]；同时风和雨等因素也会严重影响反演结果。因此将试验期间所有反演所得水面高度取均值代入求得的h(t0)，必定是包含着受多个误差源影响的水面高度均值，以此求出的测站高并非其最优解。

1.2 抗差估计求解精准测站高原理

抗差估计又称为稳健估计，是处理离群值的一种有效途径，即使在分析模型与实际模型存在偏差时仍能得到稳定可靠的结果，其利用等价权使传统的最小二乘估计具备抗干扰能力[28]。权函数是抗差估计的核心问题，就抗差目的而言，所选权函数应具备3个阶段：当观测误差很小时，采用原始权进行最小二乘处理(正常段)；当观测误差较大但并不显著时，采用降权估计处理(可疑段)；当观测值显著异常时，采用零权淘汰处理(淘汰段)。正常段可以准确揭示观测数据的内在分布模式，利用极大似然估计即可获得其最优估值；可疑段虽不能准确揭示数据的内在分布模式，但若能合理地利用其中内含的基本分布特征，对提高估值精度仍大有裨益；淘汰段提供的是有害信息，影响结果的正常估计，应对其予以剔除。本文权函数选择IGG Ⅲ方案，该方案较Huber、Tukey、Andrews权函数具备完整的3个阶段，较Hampel权函数处理方便，实用性更强[29]。

对于受多种误差源影响的GNSS-R水面高度反演值，采用抗差估计方法，将可疑段的反演值依其标准化残差分别降权，对显著异常反演值不承认其信息，取零权淘汰，以此削弱反演粗差，确保最终求解的精准测站高不受其影响。

对于任意时间段内反演所得水面高度，存在如下关系式

(9)

(10)

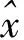
l=hGNSS+htide-hstation_0

(11)

式中,hstation_0为测站高初始值，可由试验期间所有反演所得水面高度与实际潮位求和后取平均获得。

由抗差估计理论可得如下极值条件

(12)

式中,Pi为第i个观测量权值；ρ为凸函数；νi为第i个残差。对式(12)求极值，由等价权理论得

(13)

(14)

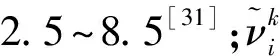
(15)

式中，σνi为νi的标准差。

本文将GNSS-R技术与抗差估计方法相结合，直接目的是求解出测站高的最优估值，进而提升GNSS-R技术的反演精度。采用抗差估计的方法削弱粗差对反演结果的影响，本质上并非从消除误差源的角度入手，而是从反演结果入手，筛选可靠的水面高度信息代入测站高度最优值的求解，以期达到与消除误差源的技术路线相近的优化效果，而操作步骤却更加简单易行，图2给出了本文的技术流程。

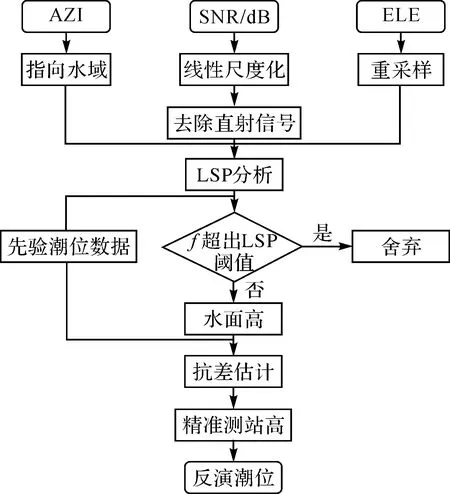
图2 技术路线

2 数据处理与分析

本文使用的试验数据来自2018年1至2月IGS GNSS连续运行跟踪站HNLC、SC02、TDAM、TPW2。各测站的经纬度、接收机类型、天线类型、整流罩类型、采样间隔见表1，各测站的周围环境、地理位置如图3所示。为验证GNSS-R潮位反演的精度，分别选取紧邻上述4个测站的火奴鲁鲁验潮站、星期五港验潮站、加尔维斯顿验潮站、阿斯托里亚验潮站的潮位数据，4个验潮站均以平均低低潮面为潮位基准面，提供每6 min更新一次的潮位数据。

图3 各测站信息

表1 HNLC、SC02、TDAM、TPW2测站信息

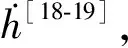
2.1 抗差估计求解精准测站高

以2018年DOY 01 PRN27号卫星L2波段的部分数据为例进行反演分析。剔除卫星时间序列中的直射信号，提取卫星高度角5°～15°、方位角205°～330°范围内的SNR残差序列并进行线性化处理，LSP分析结果中频谱振幅峰值所对应的频率即水体反射频率。图4(a)、(b)分别给出了PRN27号卫星的SNR残差序列和LSP频谱分析结果。

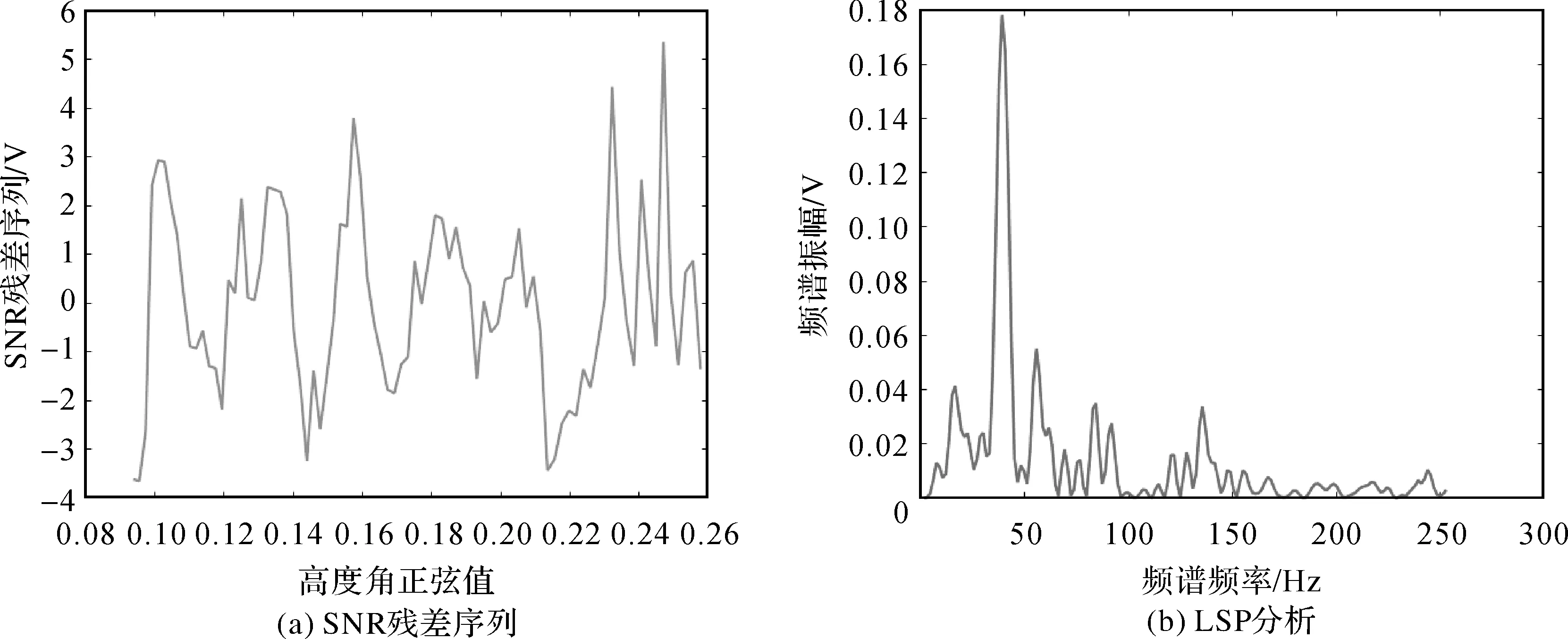
图4 PRN27号卫星提取水体反射频率

本节采用传统法(将试验期间所有反演得到的水面高度的均值与对应时刻实际潮位高度的均值相加求得测站高)和抗差估计法对HNLC、SC02、TDAM、TPW2这4个测站2018年1月的数据进行反演。高度角、方位角、反演波段、抗差因子的选取见表2。图5给出了4个测站采用传统法和抗差估计法反演所得潮位与时空同步的验潮站实测潮位的对比结果。图6给出了4个测站采用上述两种方法的相关性分析对比结果。表3给出了4个测站传统法和抗差估计法反演结果的比较。通过对比可以发现，对于4个测站，采用两种方法求得的测站高分别相差1.02、1.31、16.2、1.22 cm；RMSE方面，4个测站采用抗差估计方法后分别降低了26.7%、34.4%、84%、31.6%；相关系数方面，4个测站采用抗差估计方法后分别提高了5.6%、0.69%、41.5%、1.04%，反演潮位更加贴合实测潮位，潮位残差更小。这是因为抗差估计方法有效削弱了水面高度反演粗差的权重，阻止其参与精准测站高度的计算，以此获得测站高度最优解。可以看出TDAM测站使用两种方法反演结果差异明显，由传统法反演潮位与实测潮位序列图可知，除反演潮位整体较实测潮位略微偏低以外，绝大多数反演结果与实测结果吻合较好，只有极少数时刻反演值严重偏离实测值。由于TDAM站位于加尔维斯顿港口，常有船只来往，因此推测上述极少数偏离值是由船体噪声混入水体反射信号造成的。该部分偏离值为数不多但误差极大，造成了16.2 cm的测站高差别。而抗差估计方法可以准确识别并剔除该部分反演粗差，利用剩余正确反演值求解测站高度无偏估值，从而达到去噪目的。如图5(e)、(f)所示，利用经抗差估计去噪后求得的测站高进行潮位反演，反演潮位整体不再比实测潮位偏低，契合度大大提升，可见经抗差估计去噪后求得的测站高度更接近TDAM测站高度的真值。

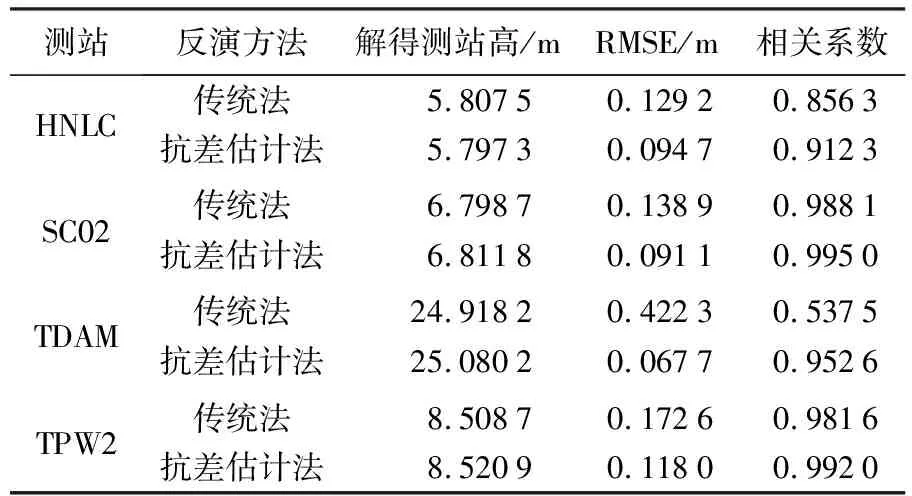
表3 各测站1月数据反演结果

图5 各测站传统法与抗差估计法反演潮位时间序列与残差

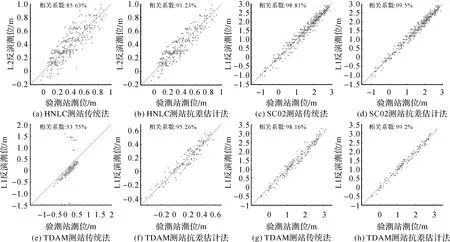
图6 各测站传统法与抗差估计法相关性分析

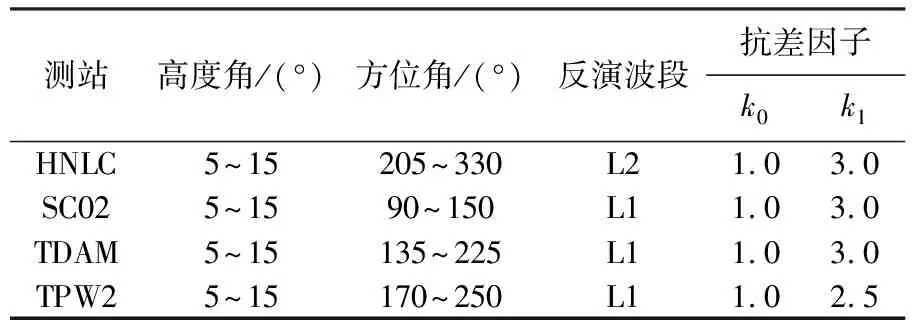
表2 各测站反演参数选择

2.2 精准测站高用于无验潮站场合的潮位反演

基于抗差估计的GNSS-R潮位反演方法的实际应用价值在于能够求出测站高度的无偏估值，在忽略测站地基极其微小沉降的情况下，可将求得的测站高度视为定值，供此后若干年间继续使用，不再需要验潮站参与潮位高度的反演。因此本节将上一节采用传统法和抗差估计法求解各测站2018年1月数据所得的测站高度作为已知值，分别直接代入2月数据中进行潮位反演(下文分别称为传统-直接法和抗差估计-直接法)。反演潮位由代入的测站高度与反演所得水面高度直接获得，无须验潮站的参与，验潮站仅用于提供真实潮位以检验两种直接法反演潮位的精度。图7、图8分别为抗差估计-直接法反演结果与实测潮位的比较，以及相关性分析结果。由于上述两种直接法的差别仅在于所使用测站高不同，因此二者反演结果除整体相差一个定值(测站高之差)外，图像走势等要素完全相同，因此不再给出传统-直接法反演结果与实测潮位的比较及相关性分析结果)。表4给出了4个测站两种直接法反演的潮位与时空同步的验潮站实测潮位的比较结果。通过对比发现，采用抗差估计法求解1月数据所得的测站高度比采用传统法的更适合2月数据的反演，4个测站的抗差估计-直接法的RMSE均小于传统-直接法的RMSE。同样的，对于TDAM测站，抗差估计-直接法较传统-直接法有着明显的优势，相关系数大幅提升，RMSE大幅减小，这也间接说明对于TDAM测站1月数据采用抗差估计求解的测站高度较传统法更接近其真值。

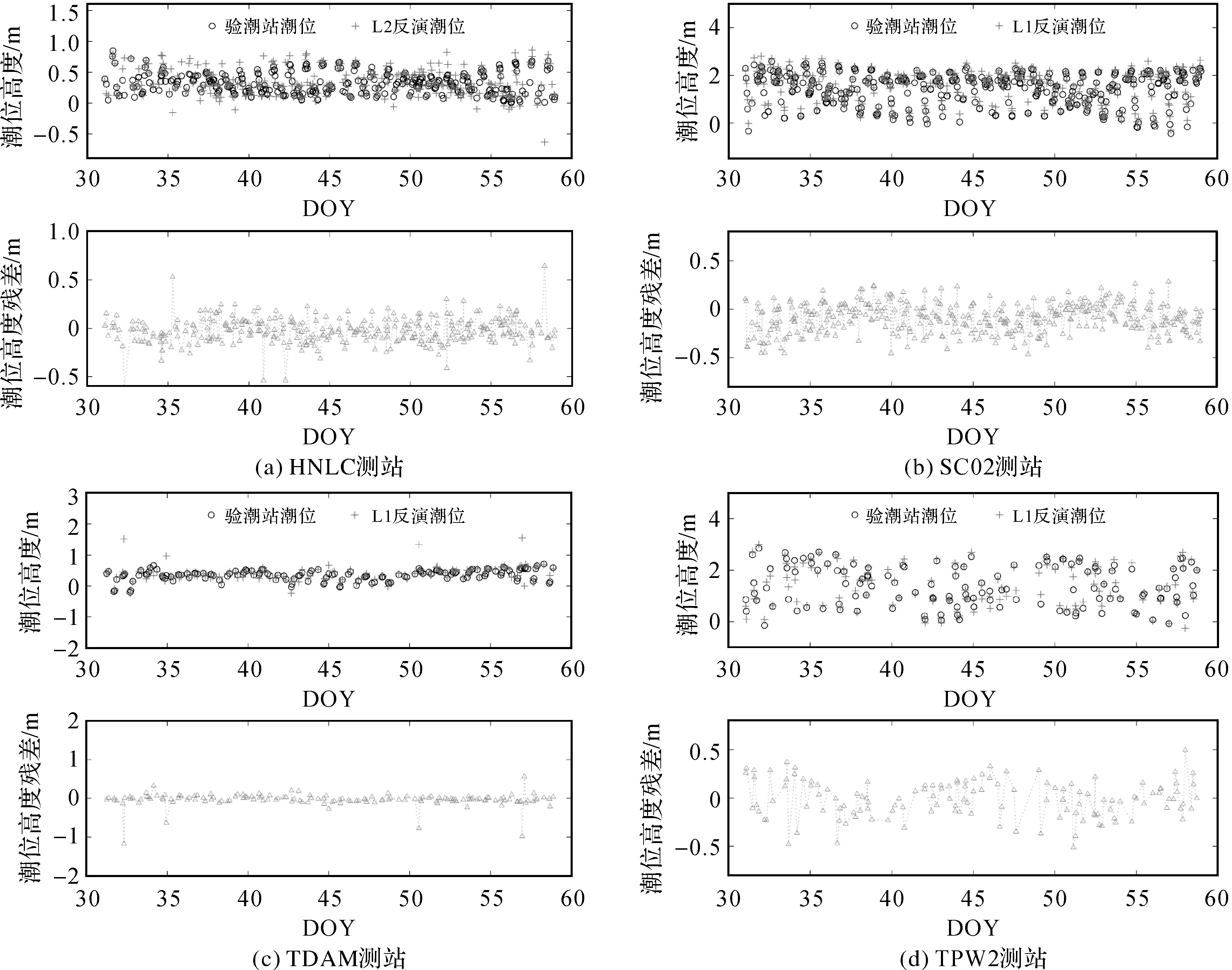
图7 各测站抗差估计-直接法潮位时间序列与残差

图8 各测站抗差估计-直接法相关性分析

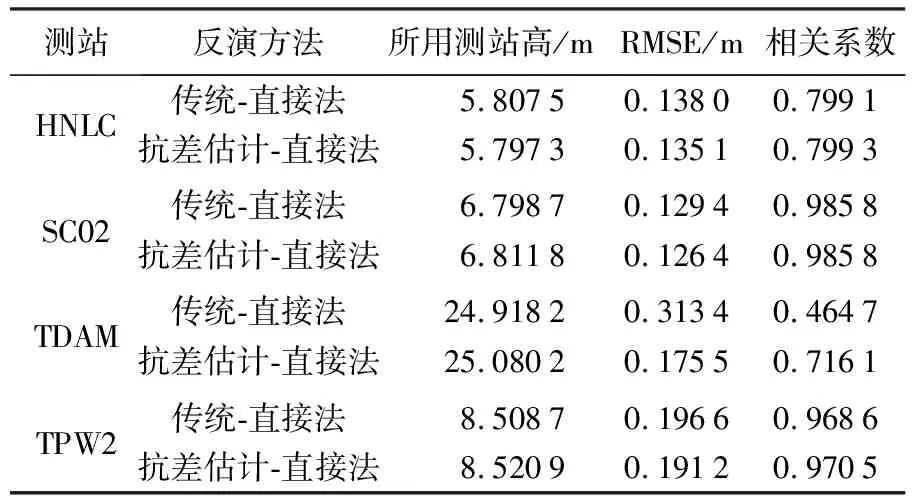
表4 各测站2月数据反演结果

由以上试验可知，采用抗差估计求解IGS GNSS连续运行跟踪站数据所得的精准测站高度，可以应用于之后无验潮站或验潮站数据中断情况下潮位的获取。4个算例中，TDAM测站明显体现出抗差估计方法的优越性，这表明测站观测数据受周围地物噪声影响越大，抗差估计的去噪优势越明显，即便是用于之后无验潮站参与情况下的潮位反演，抗差估计-直接法依旧显著优于传统-直接法。此外，表4中除TDAM测站外的其余测站两种直接法的反演精度较为接近，原因在于当无验潮站参与时，不易判断反演所得水面高度是否包含粗差，因此均未对其进行剔除；但同时，由于抗差估计-直接法所使用的测站高更接近其真值，因此在反演2月潮位数据时，其RMSE总是小于传统-直接法。另一方面，2月潮位的反演精度普遍低于1月潮位的反演精度，其根本原因在于，抗差估计-直接法使用的测站高度是求解该测站1月数据所得的无偏估值，由于各测站1月的样本数量有限，无法保证1月样本所得的测站高无偏估值等于2月样本的无偏估值，即不同的时间序列求解出的测站高无偏估值往往存在差异，因此要充分发挥抗差估计法反演潮位优势的前提是，必须具备充足的样本量，即求解测站高度无偏估值时选用GNSS观测数据的时间序列越长，所得结果越接近测站高度真值。相应地，对于某一验潮站，其拥有的历史潮位数据越多，越能发挥抗差估计的优势以求解其附近IGS GNSS连续运行跟踪站的测站高度的最优解，也就越能发挥岸基IGS GNSS测站监测潮位的能力。

2.3 抗差估计抵抗人工噪声

为更好地体现抗差估计计算精准测站高、提高GNSS-R反演精度的优势，本文还设计了一组用传统法和抗差估计法两种方法处理观测数据中包含人工噪声的试验。仍以SC02测站2018年1月的观测数据为例，向信噪比文件中加入人工噪声，添加的方案是：每隔若干个历元，在原SNR值的基础上添加某一随机数。表5给出了每隔20个历元，在原SNR值中添加不同大小的噪声后两种方法的反演结果对比。由前文分析可知，可以预测不同反演模式下的精度应满足：无人工噪声的抗差估计法>无人工噪声的传统法>有人工噪声的抗差估计法>有人工噪声的传统法，试验结果证实了这一猜想。

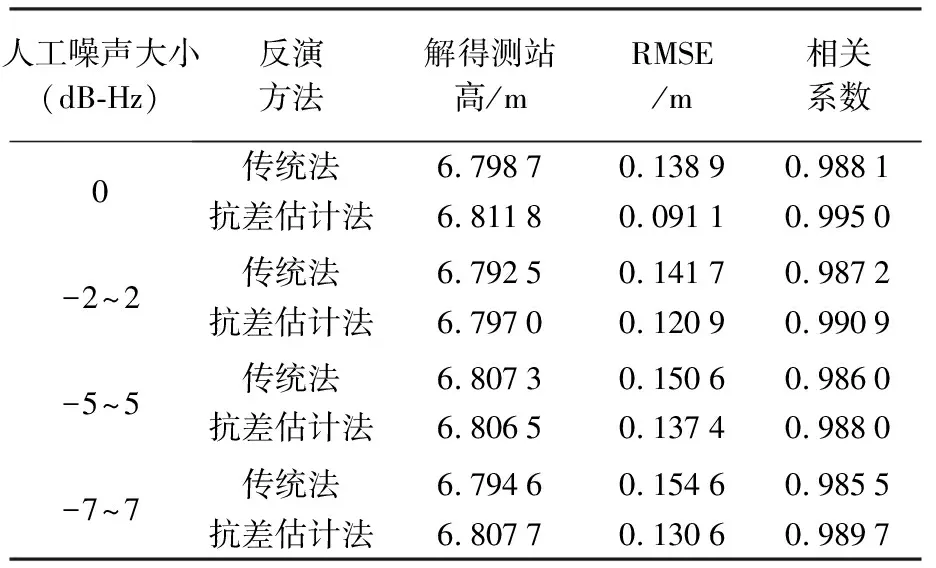
表5 传统法和抗差估计法处理恒定历元间隔的人工噪声

3 结 语

结合试验对比结果，本文有如下主要结论：

(1)针对HNLC、SC02、TDAM、TPW2测站2018年1、2月的试验数据，基于岸基IGS GNSS站的GNSS-R技术与验潮站实测数据在整体趋势上吻合较好，精度为dm级。

(2)抗差估计法能够更准确地求解出基于验潮站潮位起算面的测站高度，能够更好地减小反演的均方根误差，提高相关系数，对于受周围地物噪声影响严重的测站优化效果尤为显著。

(3)以HNLC、SC02、TDAM、TPW2测站为例进行的试验研究，证明了基于先验潮位数据求得的测站高度，可以继续用于后期无验潮站或验潮站数据中断情况下潮位的反演。

在导航定位中被视为严重影响定位精度并被人们设法抑制的反射信号，在近地水环境等领域的遥感监测中却发挥着重要作用。岸基CORS网络为开展GNSS-R技术研究提供了很好的数据支撑，可有效填补多地监测数据的空白。本文利用4个IGS GNSS连续运行跟踪站反演海面潮位数，采用抗差估计的方法，使GNSS更好地应用于潮位监测，并证明了岸基IGS GNSS站可连续对潮位变化进行监测。