基于贝叶斯估计的深海GNSS-A定位精度

明锋， 杨元喜， 曾安敏

地理信息工程国家重点实验室，西安测绘研究所，西安 710054

0 引言

高精度海底大地基准是研究海底地壳运动、水下导航定位、油气勘探和环境监测等海洋科学和海洋工程的基础(杨元喜等，2017).全球导航卫星系统-声学测距组合定位系统(Global Navigation Satellite System-Acoustic ranging，GNSS-A)可对海底参考点精确测量，能够将大地基准从陆地扩展至海底.GNSS-A技术主要包含水面GNSS动态定位和水下声学测距，最早由斯克里普斯海洋研究所的Spiess于20世纪80年代所提出(Spiess，1985)，之后其研究团队进一步提高了定位精度和观测效率，并给出了一些相关试验结果(Spiess et al.，1998；Kussat et al.，2005).

从20世纪90年代后期开始，日本的名古屋大学(Kimura et al.，2019)、东北大学(Kido et al.，2006；Honsho and Kido，2017；Honsho et al.，2019)以及日本东京海岸警卫队和东京大学联合体(Fujita et al.，2006；Ikuta et al.，2008；Sato et al.，2011，2013；Watanabe et al.，2014；Yokota et al.，2016)等研究团队持续改进GNSS-A技术，建立并维护较大规模的海底观测网，以监测环太平洋地震带的板块构造运动.法国科学家也于2014年在马尔马拉海中部的北安纳托利亚断层布设了由10个应答器组成的声学测距网络以持续监测断层活动(Lange et al.，2019).

近年来，国内也有相关学者对GNSS-A开展了理论和实验研究，得出了一些有益结论(韩云峰等，2017；赵爽等，2018；Chen et al.，2020).Yang等(2020)介绍了海底大地控制网建设关键技术，在3 km深海建立了长期大地基准站，并进行了GNSS-A观测，初步结果表明定位精度优于5 cm.之后，进一步的精化处理表明坐标分量内符精度优于0.4 cm，单程测距的均方误差为11 cm(Yang and Qin，2021).我国台湾省中山大学也致力于在冲绳海槽弧后盆地西端建设GNSS-A观测网(Chen et al.，2018).

本文简要介绍基于贝叶斯框架的GNSS-A数据处理模型，然后对某海域2019年深海GNSS-A观测数据进行重处理，重点分析航迹几何结构、参数初值以及参数估计策略对水下应答器三维定位精度的影响.

1 贝叶斯解算模型

1.1 观测方程

图1为GNSS-A基本原理和本次试验应答器配置示意图.在水上单元，沿测线航行的测量船的精确位置通过GNSS动态定位来解算，结合GNSS天线与换能器之间的臂长向量和测量船姿态向量，可得到换能器的绝对位置.在水下单元，换能器与应答器之间的几何距离使用声学测距单元测量.将换能器位置、传播时延和声速剖面数据相结合，可较为精确地确定虚拟参考点(应答器的质心)在外部参考框架下(如国际地球参考框架(International Terrestrial Reference Frame，ITRF))的坐标，进而实现了海陆基准统一.

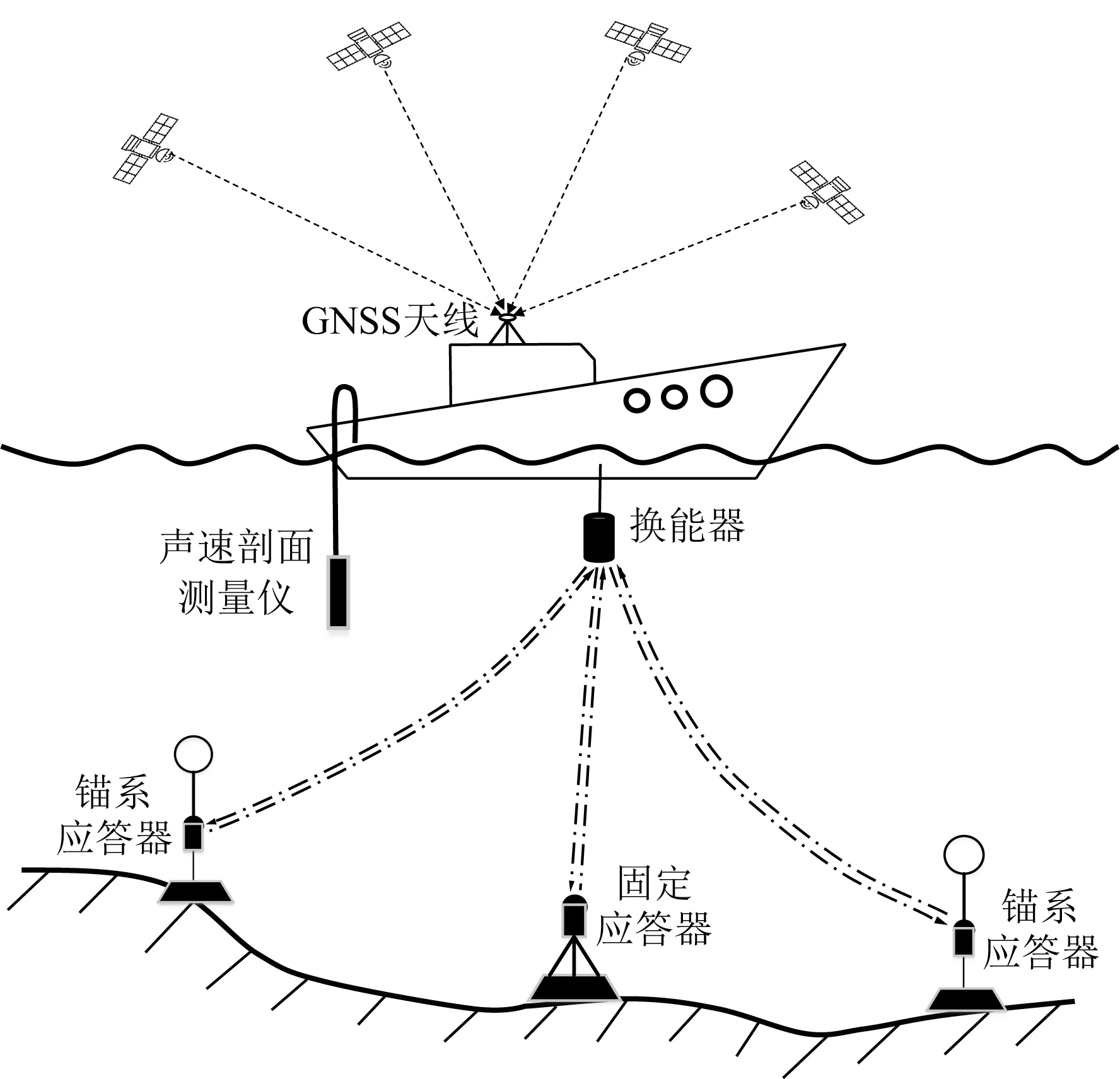
图1 GNSS-A基本原理示意图Fig.1 Schematic of the basic principle of GNSS-A

在水下声学测距中，若已知第j个海底应答器的位置Xj，换能器位置P(t)、四维声速场V(e,n,u,t)，在声速水平分层假设下，设第i个声脉冲与第j个应答器的往返传播时间为Ti，则Ti可依据Snell定律计算(Chadwell and Sweeney，2010)：

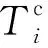
(1)

其中，ti+和ti-分别是第i个声脉冲的发送和接收时刻，P(ti+)、P(ti-)分别是换能器在ti+、ti-时刻的位置.

P(t)=Q(t)+R(Θ(t))·M,

(2)

式中，M定义在船载坐标系下，船艏为X，右舷为Y，垂直向上为Z，可事先通过经典测量手段获得.R(Θ)是将船载坐标系转换为全球坐标系的转换矩阵，即

海水中的声速是海水的温度、盐度和静压力的函数(Del Grosso，1974).本文假设声速随时间平滑变化并呈水平分层结构.这意味着在某一时刻朝不同水下应答器传播的声信号具有相同的声速剖面.然而，由于海洋洋流、潮汐等因素，实际海水的温度和盐度在水平方向上的分布并不均匀，导致声速剖面具有垂向和水平方向的时空变化.由于大部分声速变化都局限在沿声射线路径的浅层部分，因此四维声速场空间变化可以近似为时间变化，故可将V(e,n,u,t)分解为一个水平分层的静态声速剖面和一个随时间变化的扰动，即(Ikuta et al.，2008)：

exp(-γi)·τi(P(ti+),P(ti-),Xj,V0(u)),

(3)

式中，τi表示第i个声脉冲依据参考声速剖面V0(u)利用声线跟踪计算得到的模型值，V0(u)是深度的分段线性函数，γi和Xj为待估参数.当姿态值的变化足够大或臂长M测量精度不高时，也可以指定M为待估参数.exp(-γi)为改正系数，表征声速场的空间和时间扰动引起的实际时延与理论时延的差异率.γi定义为γi≡0.5×∑l=i+,i-Γ(tl,P(tl),Xj)，即声脉冲发射和接收时刻声速扰动的平均，函数Γ(t,P,X)称为声速摄动模型，其计算公式为：

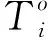
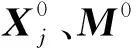
对比Yang和Qin(2021)的观测方程(公式2)，式(5)本质上仍是关于传播时延的观测方程，观测量物理意义明确，避免了由于几何距离计算不准确而产生的模型误差.如前所述，本文假设声速水平分层结构，然而如果声速结构中存在水平梯度，则梯度较慢(较快)一侧的应答器的位置会被错误地确定为较远(较近)的位置(Tomita et al.，2019).因此，式(4)中的水平梯度是GNSS-A水下应答器的水平位置估计中一个具有海洋学意义的系统偏差，解算出的水平梯度可以与物理海洋模型给出的结果相互验证.故利用式(5)既能够提取浅层海水的声速水平梯度信息，又能够解算深层海底应答器的几何位置.

1.2 参数估计

式(5)可重新改写为：

y=f(x)+e,

(6)

(7)

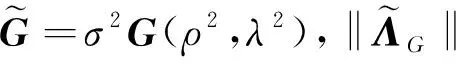
(8)

(9)

式中，m是模型参数的个数.

由于μt,μMT、ρ2,λ2分别为观测数据误差方差协方差阵或参数先验分布中包含的未知参数，称为超参数，可利用赤池贝叶斯信息量准则(Akaike′s Bayesian Information Criterion，ABIC)(Akaike，1980)确定.本文采用网格搜索法取ABIC最小时的结果为最优参数估值.

关于超参数确定和贝叶斯估计详细推导过程，可参考Watanabe等(2020)，此处不再赘叙.

2 数据处理方案

2.1 试验基本情况

试验区域位于水深约3 km的某海域.2019年7月试验共布设5个应答器，如图2所示.其中4个应答器(M01-M04)为锚系结构，分别位于正方形4个顶点，正方形边长约2 km；另1个应答器(M05)为固定站，近似位于正方形的几何中心.

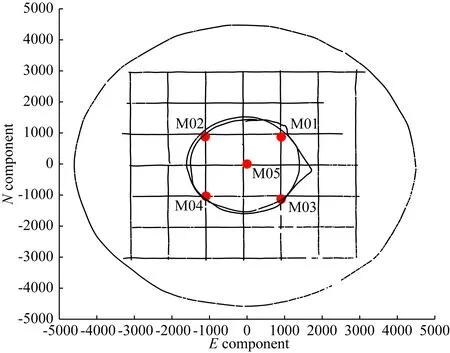
图2 5个应答器(M01—M05)点位概略分布及走航构型横轴为E分量，纵轴为N分量(单位：m).Fig.2 The general distribution of 5 transponders (M01—M05) and surveying geometry configuration The horizontal axis is the E component, and the vertical axis is the N component (unit: m).

此次试验采用“绕行观测”，测量航迹近似为圆形(大圆半径约3 km，小圆半径约1.5 km)和井字形(间距约1 km)(见图2).为减弱多普勒效应，观测过程中船速不超过4 kn.船舶配备Veripos公司的LD7接收机，GNSS天线位置采用Veripos高精度定位系统Apex结果，该系统标称的定位精度水平分量≤5 cm，垂向分量≤12 cm.采用IXSEA Octans光纤罗经测量船体姿态角，测量精度航向角0.1°，横摇和俯仰角0.01°.

走航过程中采用AML Minos X设备约每10小时进行一次往返声速剖面测量，AML Minos X的标称精度为±0.006 m·s-1，精确度为±0.025 m·s-1(Ocean Scientific International Ltd，2015).整个观测过程中共进行4次往返声速剖面测量，如图3所示.从图3可以看出，虽然4次声速剖面整体趋势一致，但在浅层海水(深度小于1 km)中单次往返测量声速变化较大，同一深度最大差异达2 m·s-1，这已远超标称精度.

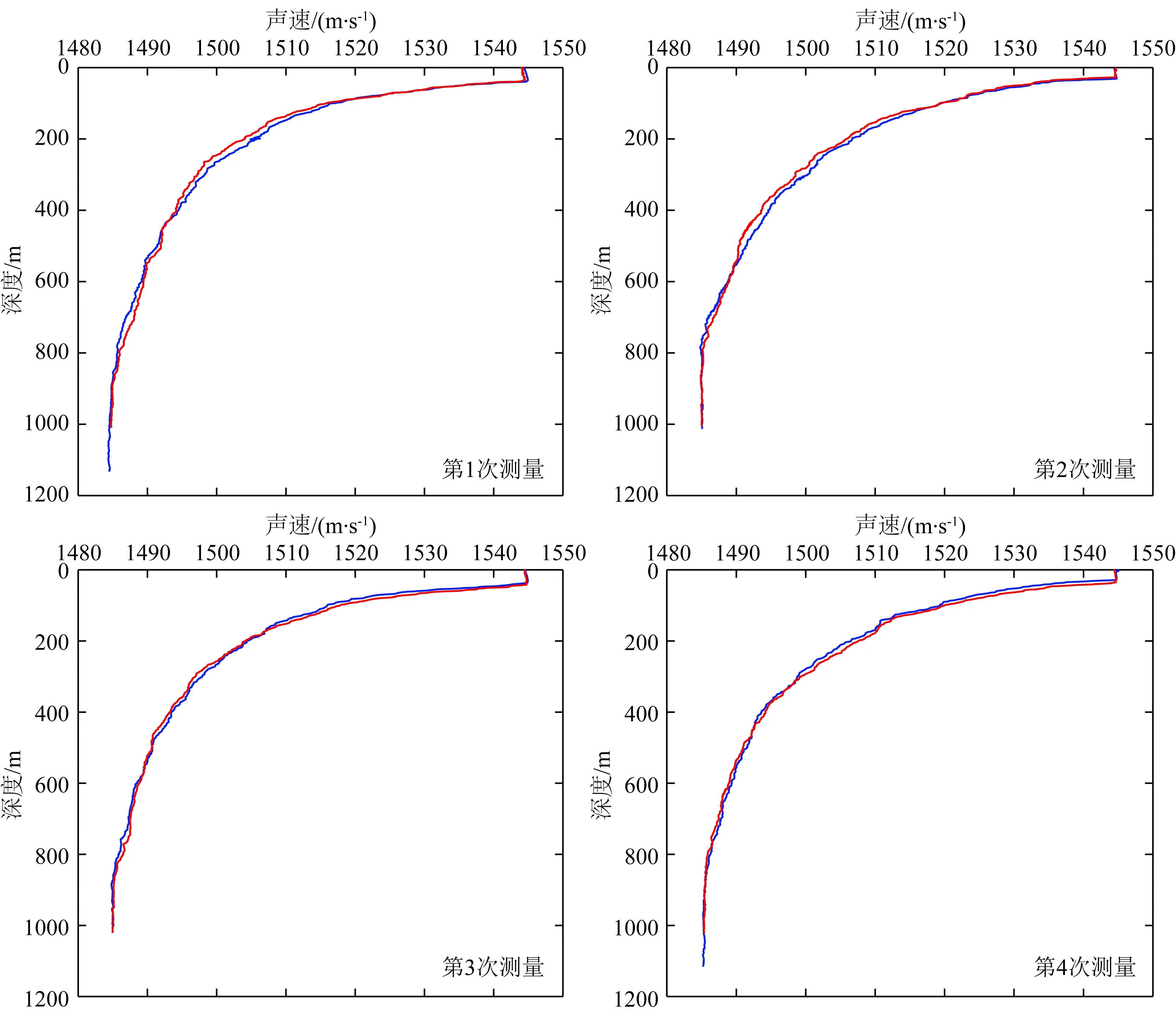
图3 不同时段观测的垂向声速剖面(深度截止至约1000 m)其中红色为前半段观测，蓝色为后半段观测.Fig.3 The vertical sound speed profile observed at different time intervals (the depth cuts off to about 1000 m) The red line denotes the first half of the observation, and the blue line denotes the second half of the observation.

2.2 参数估计策略

由1.2节可知，参数估计采用迭代法进行数值求解，当模型的非线性较强时，若初值选择不当，则最终的收敛结果可能并不是全局最优.另外，Watanabe等(2020)对应答器阵列情形进行了分析，对单个应答器定位的适用性和稳定性则没有涉及.

本文结合本次试验实际，分单站(固定站)和多站(固定站+锚系站)两种模式对上述算法的性能进行分析.对于单站模式，主要分析：(1)参数初始值对结果的影响；(2)走航图形结构对结果的影响. 单站模式下的参数估计策略分为：

策略1：不估计臂长参数M，参数初值不加偏差；

策略2：不估计臂长参数M，参数初值加0.5 m偏差；

策略3：估计臂长参数M，且参数初值不加偏差；

策略4：估计臂长参数M，且参数初值加0.5 m偏差.

需要指出的是，由于垂向分量与垂向声速剖面强相关，因此上述估计策略施加0.5 m偏移量仅针对水平分量.

对于多站模式，主要分析锚系站的定位精度，估计策略区分是否估计参数M.

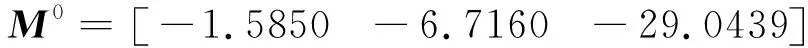
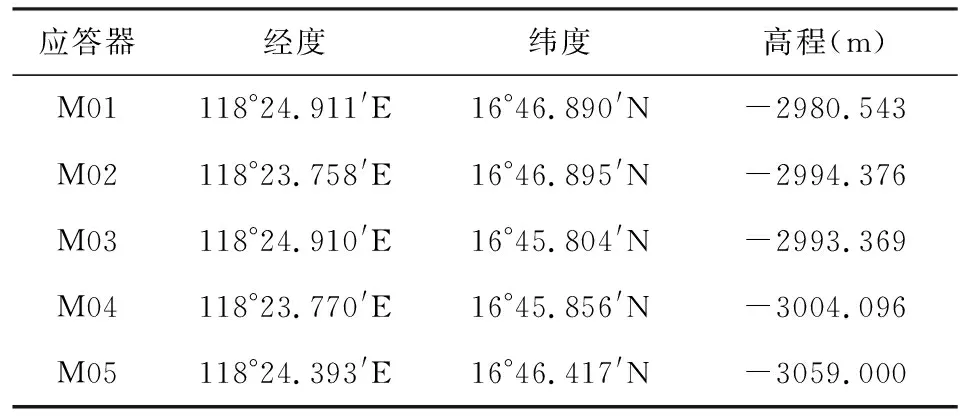
表1 应答器初始位置Table 1 The initial position of the transponder

表2 不同走航图形结构Table 2 Different surveying geometry configurations

3 结果分析

3.1 单站模式的结果

表3 单站模式的结果(M05)(单位：m)Table 3 The result of single station mode (M05) (unit: m)

3.2 多站模式的结果

多站模式下各应答器ENU三个分量的改正量列于表4.

表4 多站模式的结果(单位：m)Table 4 The result of multi-station mode (unit: m)

3.3 分析与比较

3.3.1 走航几何构型对结果的影响

从表3可以看出，对于单站模式：

(1) 大圆(方案1)和小圆(方案2)的定位精度相当，但是大圆+小圆(方案3)的精度略高；井字形测线三个分量定位精度最低(方案4)，加入圆形测线后精度有所改善(方案5)；方案6的水平分量定位精度最高，但垂向分量误差较大；方案7的定位精度仅次于方案6，但其垂向精度与方案1-3相当.

(2) 整体上来看，圆形测线定位精度要优于井字测线，特别是对于垂向分量；而圆形和井字测线组合有助于增强水平分量定位的鲁棒性.对于单一入射角的圆形测线，由于对垂向分量的观测孔径过小，无法分辨垂向分量改正量和声速偏差，从而造成两者强相关；而不同入射角组合的大圆+小圆测线(方案3)则能有效分辨应答器垂向分量改正量和声速偏差，因此垂向分量精度较高(李昭，2016).这从另一方面也说明，高精度垂向声速剖面是精确确定垂向分量的前提条件(赵建虎等，2016).

(3) 井字形测线定位精度最低，原因之一可能是走航时间相对较长(约20 h)，声速剖面采样频率偏低，声速代表性误差较大(赵建虎和梁文彪，2019)；另一个可能性较大的原因是，由于内波或其他海洋学因素导致浅层海水声速时空变化较大，而走航时间已远大于浅层海水的水平声速结构持续时间，导致同时求解应答器位置和声速水平梯度的方法已不再适用(Iinuma et al.，2021).

3.3.2 应答器位置初值对结果的影响

从表3可以看出，对于单站模式：

(1)整体来上说参数初值对结果影响较大，方案6(大圆+小圆+井字)水平分量对参数初值依赖性均较低；方案4(井字)影响最大，如前所述，这可能是由于同时求解应答器位置和声速水平梯度的方法已不再适用，此时位置参数初值施加偏差对模型求解更加不利.

(2)对于圆形航迹(方案1—3)，当初值较精确时，结果与初值偏差不大，但当初值显著偏离时，模型解算不能正确收敛到合理的估计值附近，导致时延残差增大.这表明，虽然圆形航迹水平对称，但参数初始值误差仍可导致应答器水平分量系统性偏差.系统性偏差与初值偏差的定量关系可通过模拟计算分析得到，限于篇幅，本文不做进一步的讨论.

(3)虽然本文仅对水平分量施加偏移量，但从策略2、4可以看出，在包含井字测线的方案中其对垂向分量仍有较大影响(见表3，方案4—6)，其原因还需进一步分析.

3.3.3 多站模式定位精度

从表4可以看出，相对于单站模式，多站模式的定位精度均较差，这主要是由于锚系站自身运动，而定位时则又假定其位置不变所导致.实际计算中方案4、5最终迭代已不能收敛，导致估计结果偏差较大.同时注意到，解算过程中由于假设固定站与锚系站存在相关性，因而导致固定站(M05)的定位结果相对单站模式偏差也较大.

对比锚系站(M01—M04)和固定站(M05)，可以发现不同方案中固定站的定位结果差异相对较小，水平分量差异最大为21.90 m(方案4)，最小为0.27 m(方案1)；垂向分量最大为7.76 m(方案4)，最小为0.05 m(方案1).这也说明对于高精度海底基准站定位应采取固定站模式，尽量减少因应答器自身运动而引起的误差.

3.3.4 估计臂长参数对结果的影响

对于多站模式，从表4可以看出，几乎在所有方案中，估计臂长参数对位置分量改善并不明显.这表明此种模式下，臂长参数已无法完全补偿因锚系站运动、声速剖面不准确等引起的系统误差，因而必须对锚系站运动建模或对时延残差进行函数拟合，以尽可能削弱系统误差的影响(Yang and Qin，2021).

4 讨论

4.1 定位精度估计

Yamada等(2002)采用模拟数据分析了单海底应答器的定位精度，结果表明在深海(～3 km)环境下，如果能够获得每条测线的精确声速，可以将与声学定位相关的误差抑制在大约18 cm以内(1倍中误差)；采用实测数据分析表明单应答器定位精度约为28 cm.考虑到本文贝叶斯估计中并没有纳入GNSS定位误差和姿态传感器误差，在施加3 m先验约束的情形下，应答器位置后验精度约为0.3 m，该精度与Yamada等(2002)的结果相当.

另一方面，观测时延残差与超参数的选择密切相关，且仅能反映模型的内符精度，而不能反映定位的准确度.本文算例中，如图4所示，单站模式的观测时延残差均方差(RMS)约为0.6 ms，等价于0.9 m(假设声速为1500 m·s-1)；对于多站模式，观测时延残差RMS约为4.5 ms，等价于6 m.从图4还可看出，对比固定站，多站模式各应答器残差均呈非高斯分布特征，表明仍存在潜在的系统误差.Yang和Qin(2021)采用拟合残差的方法减弱系统误差的影响，因此其结果不确定度均远小于本文的结果.

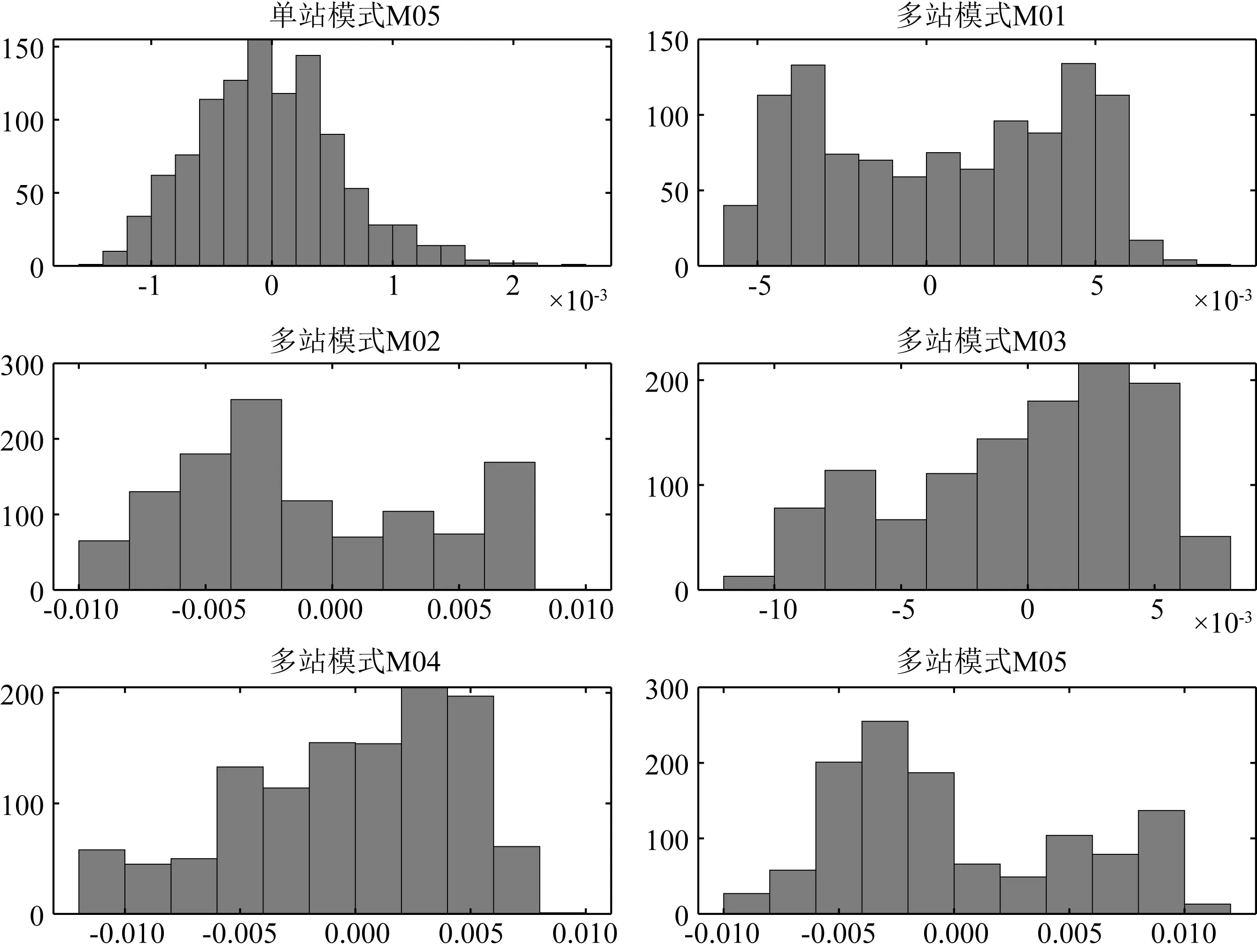
图4 单站模式和多站模式方案一的传播时延残差直方图Fig.4 The histograms of delay residual of single station mode and scheme 1 in multi-station mode

4.2 算法的数值稳定性和效率

在单站模式下，由于海底观测网没有网形约束，几何构型差，不合适的超参数易引起对角阵奇异，导致迭代计算失败；而在多站模式下，应答器观测时延之间的相关性有助于抑制方差协方差阵奇异，提高算法的数值稳定性，但同时也增加了一定的计算量.

在多站模式中，由于观测量较多，矩阵求逆占用相当大的计算资源，在保证几何构型对称分布的前提下，可对原始观测数据降低采样，以提高计算速度.

5 结论

本文利用贝叶斯估计对3 km深海GNSS-A实测数据的定位性能进行了分析，主要结论如下：

(1) 对于单个固定应答器，走航时间较短的圆形测线的定位精度最高，而走航耗时较长的井字形定位精度最低；圆形测线对参数初值要求较高.

(2) 从本文的算例可以看出，对于圆形测线或井字测线，估计臂长参数，在一定程度上都有可能提高定位结果的可靠性.然而，臂长参数估计与航迹几何构型有关，对于有些图形，估计臂长参数的能力不够，即引入不适定性问题，将会导致结果不可靠.本文算例中，由于臂长参数的先验精度较高，在测线对称分布条件下，估计该参数并不能显著提升定位精度.

(3) 固定站的定位精度远高于锚系站，应答器阵列能够显著增强解算的稳定性，但会增加计算量.

(4) 同时求解应答器位置和声速水平梯度的方法仅适用于声速水平梯度变化不大的情形，因此若采用此方法进行海底应答器定位，建议尽量减少走航时间，以满足水平声速结构近似保持不变的假设.

由于本文仅对圆形、井字形测线及其组合进行了分析，限于观测条件没有对其他类型测线进行分析.另外，由于GNSS-A走航观测需耗费大量船时，如何确定最优的海底应答器分布以及对应的走航几何构型，既能提高观测效率，又能保证定位精度仍需进一步分析研究.