三支链六自由度并联骨外固定支架刚度优化设计

傅雨璇，霍欣明，齐 杨，宋轶民, ，孙 涛，张 弢

（1.天津大学机械工程学院，天津 300350；2.天津职业技术师范大学机械工程学院，天津 300222；3.天津仁爱学院机械工程系，天津 301636；4.天津市天津医院，天津 300211）

骨折创伤是现代人日常生活中常见的健康问题之一[1].骨折治疗包括复位与固定，传统的治疗方法存在复位精度差、易造成二次创伤与并发症、延迟愈合等局限[2].随着机器人学与现代医学的交叉融合，基于并联外固定支架的微创骨折复位与固定方案受到普遍关注.并联外固定支架包括两个环与连接环的多条可调支链.复位时，利用克氏针或螺纹针分别连接骨折断端与环，医师根据患者骨折情况规划复位轨迹，基于此计算支链的长度变化，通过调节支链的长度改变环的相对位姿，实现骨折断端的复位.并联外固定支架可精准调节骨折断端的相对位姿，复位后无需二次拆除，具有治疗周期短、适应症广等优势，被认为是骨折复位与固定的优势解决方案[3].

并联外固定支架最早可追溯至20世纪中期.前苏联医生 Ilizarov观察到牵拉操作对骨生长的促进作用，提出拉应力法则，发明了一种模块化的环形外固定支架 Ilizarov[4].1994年，美国骨科医生Charles和工程师Harold将Stewart六自由度并联机构引入骨折治疗，设计出 Taylor支架[5].类似地，基于并联机构的外固定支架被相继推出，例如可快速拆装的 Ortho-fix支架[6]、高刚度高精度 Ortho-SUV支架[7]、自动化调节程度高的 Orthospin机器等[8].纵观国内外现有并联外固定支架，均为六自由度六支链机构.尽管此类六支链并联外固定支架已取得成功应用，但骨折复位手术前患者拍摄骨折 CT影像时，6条支链易造成伪影，影响患者骨折部位的图像分析，不利于骨折复位轨迹规划.目前，针对此问题的解决方案或是采用非金属材料制造支链，或是采用智能图像分割与提取方法.本文提出了从原始机构创新设计并联外固定支架的思路，设计出一个三支链六自由度并联外固定支架，保证支架调姿能力的同时减少支链的数目，从源头上解决 CT伪影的问题.所提出的三支链六自由度并联外固定支架拓扑组成为 3-SPRP.其中，S、P、R 分别代表球铰链、移动副和转动副.每条支链内的移动副均可通过丝杠-螺母结构驱动，从而使环产生空间三平动与三转动的相对运动.由于此支架用于人体下肢骨折的复位与固定，为使支架受人体重量作用产生的变形较小，需要对支架进行刚度优化设计.

三支链六自由度并联外固定支架的刚度优化设计首先需建立支架结构参数与支架整体刚度性能的映射模型.基于有限元分析软件的数值建模法[9]可精准构建支架在外载荷作用下的变形，但无法反映参数变化对支架刚度性能变化的影响，难以进行参数化建模，仅适用于设计完成后的刚度校核.针对此问题，有学者提出采用结构矩阵进行并联机构解析刚度建模的思路[10]，由标准梁单元的结构矩阵列写刚度表达式，通过单元节点间的耦合或变形协调条件组集得到整机刚度模型.此方法可实现并联机构的参数化刚度建模，但并联外固定支架的球铰链与转动副无法近似为规则单元，基于结构矩阵法得到的刚度模型与有限元刚度模型差别较大.因此，本文采用半解析建模法[11]进行三支链六自由度并联机构的参数化刚度建模.基于有限元模型获取非规则零件的柔/刚度模型，由结构矩阵法建立待设计零件的柔/刚度解析模型，结合雅可比矩阵、虚功原理和虎克定律获得支架整体的参数化刚度模型.相比于传统的只考虑受力方向变形的刚度建模方法，本文采用 n(n≤6)自由度虚拟弹簧表征零部件输出端的弹性变形，所得的考虑非对角线元素影响的柔度矩阵将有助于建立更准确和完备的整机刚度模型.

三支链六自由度并联外固定支架的刚度优化设计还需考虑刚度与质量间的关系.若仅以支架刚度性能为单一的优化目标，为追求支架的高刚度性能表现，优化参数极有可能导致支架质量的增加，这将与并联外固定支架的轻质便携设计要求相背离.因此，本文将支架质量与刚度均视为优化目标开展多目标优化设计，定义刚度与质量的最佳匹配关系，据此进行参数优选.

围绕上述问题，本文针对一种三支链六自由度并联外固定支架 3-SPRP开展半解析刚度建模，基于此进行刚度与质量的多目标优化设计.第 1节介绍 3-SPRP并联外固定支架的组成并开展运动学分析；第2节进行 3-SPRP并联外固定支架的半解析刚度建模，由典型位姿下的支架仿真对比验证模型的有效性；第 3节定义刚度性能评价指标与质量指标，开展多目标优化设计，提出最小距离法确定刚度与质量指标的最佳匹配，实现参数优选.

1 机构简介与运动分析

1.1 3-SPRP并联外固定支架简介

3-SPRP并联外固定支架如图1所示.该支架由静平台、动平台和 3条相同且呈空间对称分布的SPRP支链构成.SPRP支链通过 S副、P副分别与静、动平台连接.每条SPRP支链内的2个P副方向相互垂直.由于 SPRP支链为六自由度支链，驱动 6条支链内的 P副可使动平台相对于静平台实现六自由度位姿调节.

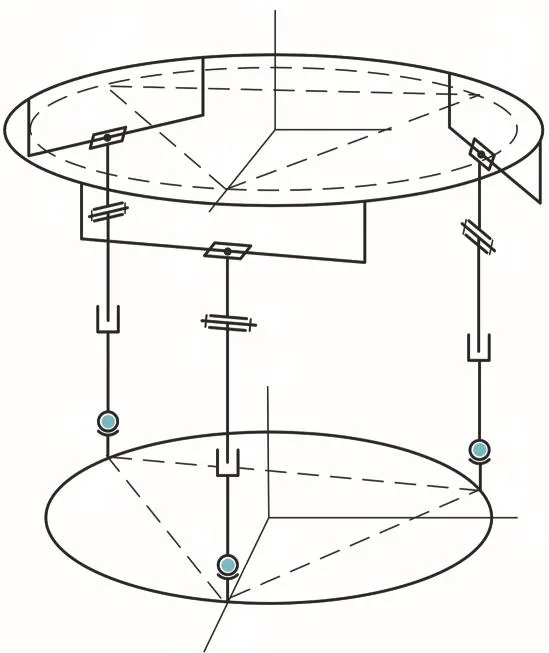
图1 3-SPRP并联外固定支架简图Fig.1 Schematic diagram of 3-SPRP parallel external fixation frame

3-SPRP并联外固定支架的虚拟样机模型如图2所示.静、动平台呈环状结构，在圆周方向上等相位布置相同直径的通孔，用以紧固克氏针或螺纹半针，达到连接骨折断端的目的.将每条支链内的 S副拆分为R副与U副，其中R副的轴线方向垂直于静平台平面.第1个P副采用双套筒＋丝杠螺母结构，具备快速安装与精准调节功能.内套筒的下端设计外螺纹，与外套筒的内螺纹实现螺纹连接，实现精准的移动量调节.在病患部位安装支架时，医师可根据病人的骨折情况将外套筒旋合至适宜位置，通过锁紧螺钉使内外套筒相对固定即可实现快速安装.转动纵向驱动螺母可使纵向丝杠相对于内套筒实现轴向移动.内套筒上设置最小单位为 1mm 的刻度线，纵向丝杠下端安装限转示数销，依据限转示数销的刻度位置进行读数和移动调节.纵向驱动螺母底面安装小型碰珠，内套筒接触面上设置圆周均匀分布的4个小孔，当碰珠与小孔同轴时有明显卡顿触感，可实现0.25mm 精度的调节.丝杠上端与连接套固接，通过销轴实现R副的转动.第2个P副采用导轨滑块＋丝杠螺母结构.导轨上设置最小单位为1mm的刻度线，方向与丝杠轴线方向平行.转动横向驱动手轮使横向丝杠转动，带动滑块沿横向导轨移动.拧紧 2个横向锁紧螺钉可限制横向丝杠转动，进而锁定滑块的横向移动.滑块下端与转动销轴配合.滑块上设置最小单位为 0.9mm的刻度线，可实现 0.1mm的精准调节.

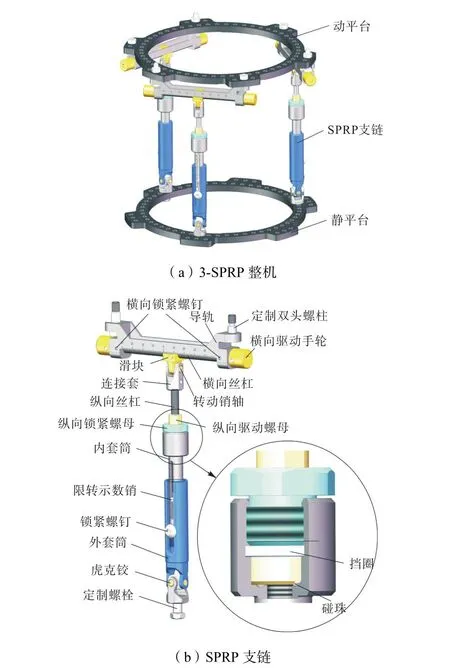
图2 3-SPRP并联外固定支架虚拟样机Fig.2 Virtual prototype of 3-SPRP parallel external fixation frame

1.2 位置逆解

为表示机构的运动，定义如图1所示的坐标系与符号.Ai、Bi、Ci(i=1,2,3)分别表示第i条支链的S副中心、R副中心和第2个P副的滑块中心点.Ai、Ci在静、动平台平面的投影为 Ai′、Ci′.△ A1′A2′A3′和△C1′C2′ C3′均为等边三角形.定义等边三角形的中心点O和点P为静坐标系和动坐标系的原点.令OA1′为静坐标系Oxyz的 x轴，z轴垂直于静平台平面，y轴满足右手定则.类似地，动坐标系Puvw的u轴为PC1′方向，w轴为动平台平面法线方向，v轴满足右手定则.

构造3-SPRP并联机构的闭环矢量方程为

式中：rP、表示在静坐标系下点 P、点 Ai的位置矢量；q1,i、w1,i为第 1个 P副的移动量与单位方向向量；h3为点Bi与点Ci间的距离；w表示动平台平面法线方向的单位方向向量；q2,i、w2,i为第2个P副的移动量与单位方向向量；R表示动系Puvw相对于静系Oxyz的旋转矩阵；rCi表示在动坐标系下点Ci的位置矢量.

式中：r1表示静平台半径；h1表示点 Ai与点 Ai′的距离；r2表示动平台半径；rCi′表示在动坐标系下点Ci′的位置矢量；α、β、γ分别表示动平台旋转矩阵的RPY 角；h2表示点与点Ci的距离.

支链内第1个P副与第2个P副方向始终互相垂直，可构造约束方程为

将式(2)代入式(1)中，可求得 3-SPRP并联机构的位置逆解表达式为

1.3 运动/力映射模型

基于瞬时旋量理论[12]可得 3-SPRP并联机构的速度模型为

式中：si,j( j= 1 ,2,… ,6 )表示支链中第 j个运动副单位方向向量；rS,i和rR,i分别表示S副和R副中心的位置向量；vi,j和ωi,j分别表示移动副的线速度和转动副的角速度大小.

SPRP支链为无约束支链，因此支链对动平台无约束力作用.支链内的 2个 P副为主动关节，支链具有 2个驱动力螺旋.由瞬时螺旋理论可知，锁定主动关节，由支链内其他运动副的运动螺旋求出的反螺旋即为驱动力螺旋.因此，分别锁定第 1个、第2个P副，求得驱动力螺旋为

式中rS,i= rAi.

整理式(6)可得3-SPRP并联机构的力模型为

式中

2 静刚度建模

2.1 刚度建模流程

静刚度衡量 3-SPRP并联外固定支架在人体重量等外载荷作用下抵抗变形的能力.3-SPRP并联外固定支架的刚度模型需考虑静平台、SPRP支链与动平台的柔度，结合受力/变形传递关系，将各部件刚度组集获得整机刚度.为分析零件的线弹性变形，假定零件为刚体，其柔性采用零件输出端的 n(n≤6)自由度虚拟弹簧表示.n的取值与零件输入端的运动副相关.若运动副的自由度为 m，则n=6-m，表示零件在许动方向上的刚度为 0.3-SPRP并联外固定支架的刚度建模流程可归纳如下：①建立各零件的局部坐标系，根据零件结构特征由解析法或有限元分析法获取零件柔度矩阵；②支链内零件的柔度均转换至静坐标系下，进行线性叠加得到支链柔度；③根据虚功原理、虎克定律、运动/力映射模型，计算 3条支链转换至静坐标系下的刚度矩阵；④将静平台、支链与动平台的柔度进行线性叠加，建立整机在末端参考点处的刚度模型.整机刚度建模思路如图3所示.

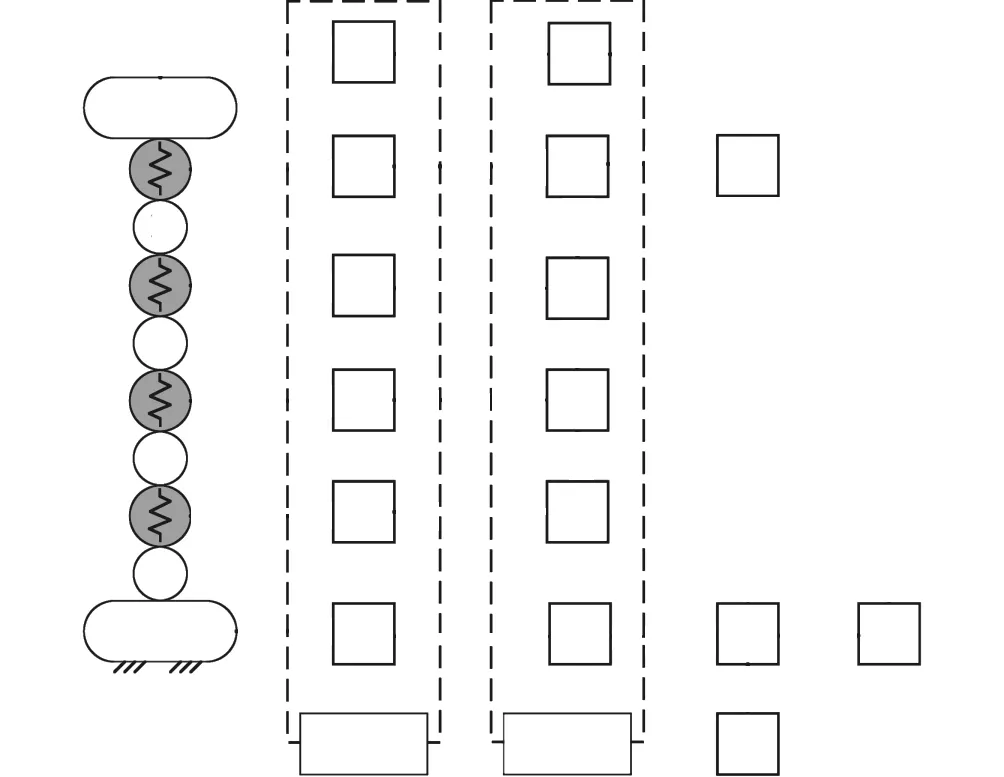
图3 3-SPRP并联机构刚度建模流程Fig.3 Stiffness modeling of 3-SPRP parallel mechanism

2.2 支链柔度模型

根据整机刚度建模流程，首先建立SPRP支链内各零件的参考坐标系，如图4所示.

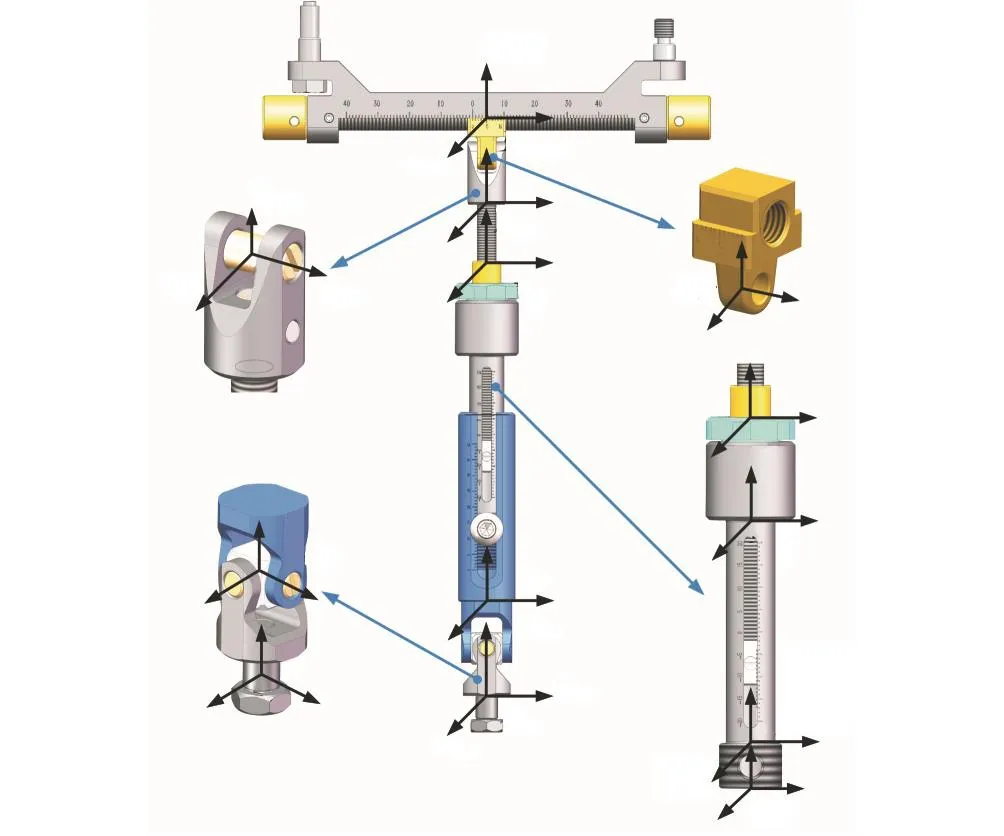
图4 SPRP支链各零部件参考坐标系Fig.4 Component reference frames of the SPRP limb

S副由转动副和虎克铰实现，包括定制螺栓、虎克铰近端零件、中心十字轴与虎克铰远端零件.由于定制螺栓、虎克铰近端零件和虎克铰远端零件是非标准零件，其柔度矩阵由有限元软件 Ansys Workbench直接提取.

如图5所示，以虎克铰近端零件为例阐述如何通过软件提取零件柔度矩阵.由于近端零件与静平台间通过定制螺栓连接，在近端零件螺纹孔处设置转动约束.近端零件的输出端是两段同轴的通孔.在输出端沿局部坐标系方向依次施加单位力与单位力矩，由对应力作用下的变形提取柔度矩阵Cs2,i.

图5 虎克铰近端零件柔度提取（负载为x方向单位力）Fig.5 Extract deformation of proximal part of the hook hinge（the load is 1N in the x direction）

中心十字轴可简化为十字梁单元，具有二自由度转动能力，在局部坐标系下其柔度矩阵可解析表达为

将 S副各零件的柔度矩阵转换至静系，需求解S副各零件局部坐标系相对于静坐标系的转换矩阵.第1个P副的移动方向为si,4，将其设为S副输出端的wouts.由于第 2个 P副的移动方向si,6与 R副平行，将si,6设为 S副输出端的vouts.则 S副输出端的uouts由si,4与si,6叉积获得，即

S副的输入端与静坐标系间的转换关系为

S副的姿态转换矩阵具有如下关系：

式中 Rsα,i、Rsβ,i、Rsγ,i分别表示绕 S 副 u 轴、v 轴和 w轴转动的姿态转换矩阵.

根据式(12)可求得转动角度αs,i、βs,i和γs,i分别为

式中 Rs,i(i,j)表示Rs,i的第i行第j列元素.

因此，定制螺栓、虎克铰近端零件、中心十字轴和虎克铰远端零件的姿态变换矩阵分别为

根据式(12)、(14)和(15)可得 S副各零件的伴随矩阵

将 S副各零件在局部坐标系下的柔度矩阵转换至静坐标系下，叠加可得S副的柔度矩阵为

称第1个P副为纵向P副，主要由外套筒、内套筒、驱动螺母、锁紧螺母和纵向丝杠组成.各个零件局部坐标系的定义如图4所示.由于纵向 P副各零件的结构外形较规则，可将各零件视为悬臂梁.在局部坐标系下，各零件的柔度矩阵可解析表达为

由于纵向 P副各零件仅产生相对移动，零件的姿态转换矩阵仍与 S副输出端的姿态转换矩阵相同，则

因此，纵向P副各零件的伴随矩阵为

式中各局部坐标系原点的位置向量为 rp1,i= rAi+h1si,4，rp2,i= rp1,i+lp1,isi,4，rp3,i= rp2,i+lp2,isi,4，rp4,i=rp3,i+lp3,isi,4，rp5,i= rp4,i+lp4,isi,4，rp6,i= rp5,i+lp5,isi,4.

将纵向 P副各零件在局部坐标系下的柔度矩阵转换至静坐标系下，叠加得纵向P副的柔度矩阵为

如图4所示，R副由连接套和转动销轴组成.由于连接套结构非规则，其柔度矩阵Cr1,i可由有限元软件提取.转动销轴可简化为简支梁单元，其柔度矩阵的解析表达式为

连接套和转动销轴的姿态变换矩阵可由关节轴线和动平台法线方向向量直接获得，即

由式(23)、(24)可求得连接套和转动销轴的伴随矩阵分别为

式中：各局部坐标系原点的位置向量 rr1,i=rp6,i+lp6,isi,4；rr2,i= rAi+q1,isi,4.

将连接套和销轴在局部坐标系下的柔度矩阵转换至静坐标系下，叠加可得R副的柔度矩阵为

称第2个P副为横向P副，主要由横向导轨、滑块和横向丝杠组成.滑块和横向导轨为非规则零件，在局部坐标系下柔度矩阵Cd1,i和Cd3,i由有限元软件直接提取.横向丝杠视为两个并联的悬臂梁，其柔度矩阵解析表达式为

式中矩阵各项元素的表达式参考式(18).横向丝杠悬臂梁单元的长度分别为 ld2,i+q2,i和ld2,i- q2,i.

横向 P副各零件局部坐标系的姿态变换矩阵可根据P副移动方向向量与动平台法线方向向量获得

因此，悬臂梁单元的伴随矩阵可表示为

其中零件局部坐标系原点在静系下的位置向量为

故悬臂梁单元转换至静坐标系下的柔度矩阵为

由于悬臂梁单元并联连接，横向丝杠的柔度矩阵可表示为

将横向导轨、滑块和横向丝杠在局部坐标系下的柔度矩阵转换至静系下，线性叠加获得横向 P副的柔度矩阵为

支链内各个零部件为串联连接，则零部件的柔度矩阵在同一坐标系下表达，叠加可得SPRP支链的柔度矩阵

2.3 整机刚度模型

假设外力施加在动平台参考点处，构建支链末端与参考点处的虚功方程为

式中：Sw和St分别为作用于动平台参考点的力螺旋和相应的变形螺旋；f和ρ表示支链末端的力和虚位移.

支链末端的力与变形满足虎克定律，则

将机构关节空间与操作空间的力映射模型代入式(38)，获得3条支链在操作空间的刚度矩阵为

静、动平台Cpl和Cb在其局部坐标系下的柔度矩阵由有限元软件提取.局部坐标系相对于静坐标系的转换矩阵为

式中I3为三阶单位阵.

静、动平台转换至静坐标系下的柔度矩阵为

由于静平台、SPRP支链与动平台为串联连接，可由变形叠加原理获得 3-SPRP并联外固定支架在静坐标系下的刚度矩阵，将其转换至末端参考点处，得

2.4 算例验证与分析

分别选取 3-SPRP并联外固定支架的 6个典型位姿，导入有限元分析软件中进行刚度仿真实验，对比理论模型在对应位姿下的各向线刚度值，验证理论建模方法的有效性.3-SPRP并联外固定支架的尺度和截面参数如表1所示.

表1 3-SPRP并联机构尺度和截面参数Tab.1 Dimensional and sectional parameters of 3-SPRP parallel mechanism

将 3-SPRP并联外固定支架的典型位姿分为 2组.第 1组取α=β=γ= 0°，x = y =0mm，z分别取208mm、228mm 和 248mm 3个测点.第 2组在z = 228mm的平面上沿半径为 40mm的圆周选取间隔90°的 3个测点.有限元模型和理论模型的各向线刚度对比如表2和表3所示.

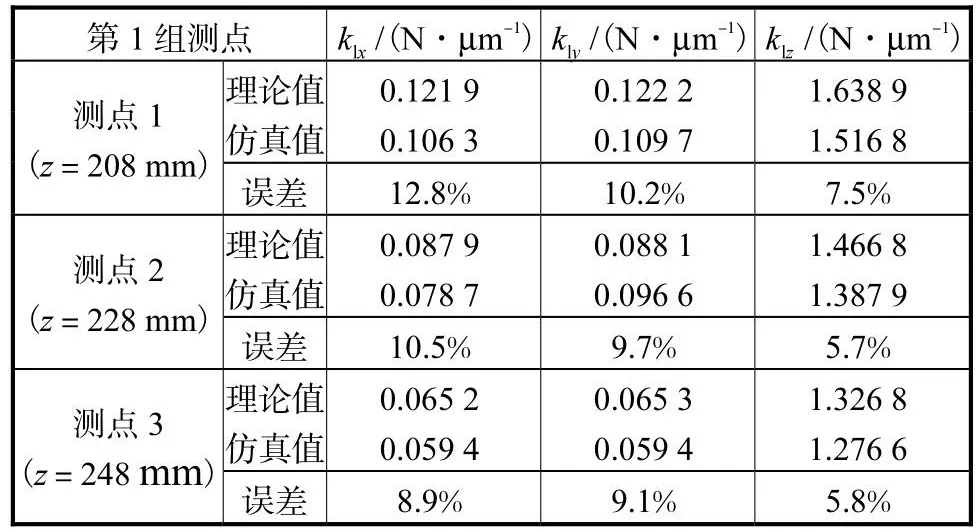
表2 各测点各向线刚度对比（ α =β=γ= 0°，x=y=0mm）Tab.2 Comparison of analytical and simulations value of linear stiffness in certain measuring points（α=β=γ= 0°，x = y = 0mm ）

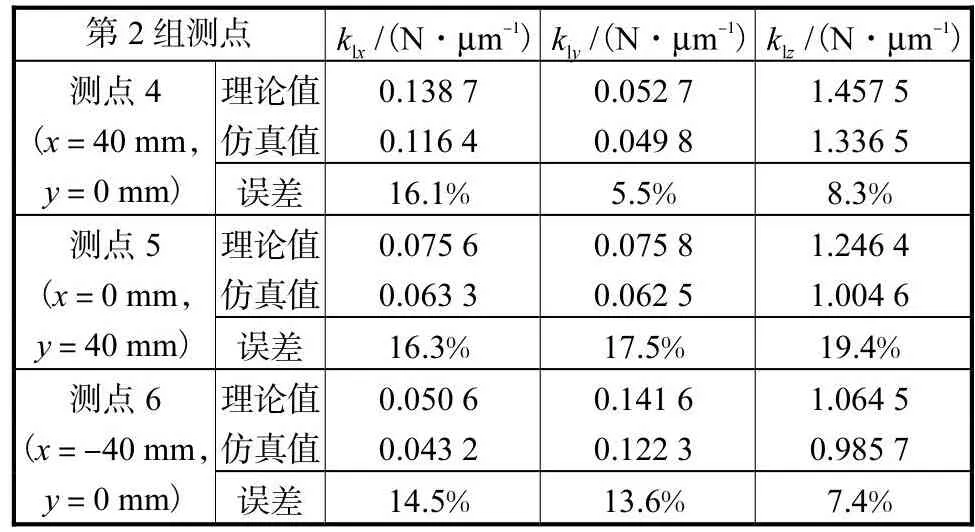
表3 各测点各向线刚度对比（ α=β=γ= 0°，z=228mm）Tab.3 Comparison of analytical and simulations value of linear stiffness in certain measuring points（α=β=γ= 0°，z = 228mm ）

可见，3-SPRP并联外固定支架的理论刚度与仿真刚度均呈现相同的规律：x、y向线刚度在同一z平面内取值接近，z向线刚度约为x、y向线刚度的2倍且随着高度值的增大而减小.6个典型位姿处的各向理论刚度值普遍高于仿真刚度值，其原因是理论刚度模型忽略了凹槽、螺纹等结构.总体而言，理论刚度与仿真刚度的变化趋势一致，且两者的误差在 20%以内，表明了 3-SPRP并联外固定支架刚度模型的有效性.

3 刚度与质量优化设计

3.1 刚度与质量优化设计流程

以高刚度为目标的机构设计通常伴随着机构质量的增加.高刚度大质量的性能表现与并联骨折外固定支架的便携可穿戴需求冲突，因此必须将刚度与质量均视为优化目标，开展轻质高刚的并联骨折手术机器人设计.当机构的参数发生变化时，机构的刚度与质量性能随之改变，两者改变的趋势相反，存在相互约束竞争的关系.为客观评价刚度与质量随机构参数的变化规律，采用多目标优化方法进行 3-SPRP并联外固定支架的优化设计.整机优化流程如图6所示.

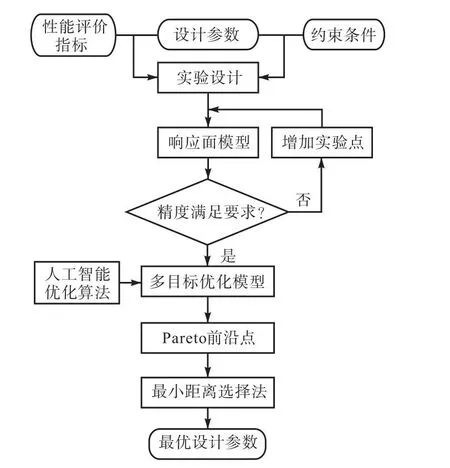
图6 3-SPRP并联外固定支架多目标优化设计流程Fig.6 Procedure of multi-objective optimization of 3-SPRP parallel external fixation frame

首先，基于刚度模型与质量模型定义量化性能评价指标作为优化目标函数.其次，将机构的尺度与截面参数视为优化变量，以工作空间边界为几何约束条件、z向最小刚度为性能约束条件，构建刚度与质量双目标优化模型，获得 Pareto前沿后，提出最小距离法确定刚度与质量的最佳匹配关系，对应的参数取值即为优选的参数.

3.2 性能评价指标

施加于 3-SPRP并联外固定支架末端参考点的外载荷与对应变形所做的功将转化为机构存储的瞬时能量.通过瞬时力与瞬时变形的乘积可求解瞬时能量为

瞬时变形能小，表示机构的变形小，则机构刚度大.由于瞬时能量对于线刚度与角刚度的单位均为J，以其表征并联外固定支架刚度可有效统一量纲，物理意义清晰.

结合柔度矩阵，3-SPRP并联机构局域刚度性能评价指标可表示为

式中：ρl,jl和ρa,ja分别表示力和力矩的系数；δl,i,jl和表示柔度矩阵特征向量的系数；λc,i表示柔度矩阵的特征值.

为评估3-SPRP并联机构在工作空间内的综合刚度性能，将任务工作空间中η的均值作为全域刚度性能评价指标，即

式中V为工作空间的体积.

3-SPRP并联外固定支架的质量模型可分为规则零件与非规则零件.非规则零件的质量由 solidworks软件获得，规则零件的质量根据密度与体积求解.将两者叠加可获得 3-SPRP并联外固定支架的质量模型，可直接将其作为质量优化目标.

3.3 多目标优化设计

结合设计需求和工程经验，定义 3-SPRP并联外固定支架设计变量如下：动、静平台半径r，纵向丝杠直径dp6，横向丝杠直径dd，十字中心轴直径ds，转动销轴直径dr.设计变量取值范围如表4所示.

表4 设计参数取值范围Tab.4 Range of design variables

以z向线刚度最小值 4 × 1 05N/m为性能约束条件，以给定工作空间边界为几何约束条件.据此，3-SPRP并联外固定支架多目标优化设计模型可表示为

采用粒子群优化算法，进行 3-SPRP并联外固定支架多目标优化设计计算，共获得564个非支配点组成Pareto前沿，如图7所示.

由图7可知，刚度指标越大，3-SPRP并联外固定支架刚度越小，此时质量向减小的趋势变化，表明Pareto前沿上刚度与质量间存在竞争关系，多目标优化设计无法取得两个目标均最优的参数集.若仅以刚度指标作为单一的优化目标，其优化结果如图7中红点所示，此时支架质量接近 1kg.考虑到 3-SPRP并联外固定支架作为长期穿戴式设备对轻质量的需求，仅考虑刚度的优化结果并不是最佳选择.为获取刚度与质量的最佳匹配关系，通过刚度与质量指标的最小值构造虚拟理想点，如图7中黑点所示.虚拟理想点位于 Pareto前沿的非可行解空间，表明无论机构参数如何变化均无法达到理想的刚度与质量值.分别计算 Pareto点与虚拟理想点的距离，最小距离对应的 Pareto点具有最佳的刚度与质量匹配关系，如图7中的绿点所示.将最小距离点对应的设计变量值结合加工经验进行圆整，最终取值如表5所示.

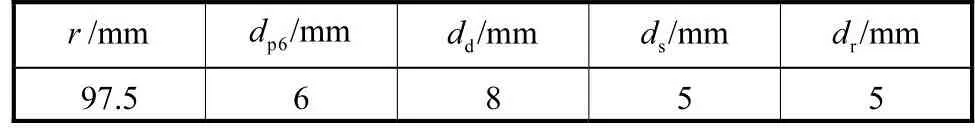
表5 最优设计参数取值Tab.5 Optimal design variables

图7 3-SPRP并联机构多目标优化设计的pareto前沿Fig.7 Pareto front of multi-objective optimization of 3-SPRP parallel mechanism

将优化后的参数代入刚度与质量模型中，对比优化前后虚拟样机的性能表现.优化后，3-SPRP并联外固定支架质量近似为 0.889kg，相较于优化前仅增加24g.给定z平面比较优化前后各向线角刚度的变化，如图8所示.优化后的刚度值较优化前普遍提升50%左右，表明本设计方法可在质量增加幅度较小的前提下，较大幅度提高3-SPRP并联机构的刚度.

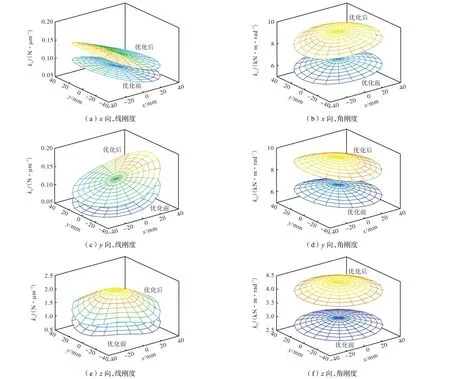
图8 优化前后刚度分布对比Fig.8 Comparison of stiffness distribution before and after optimization

4 结 论

针对现有六支链并联骨折外固定支架普遍存在的临床问题，本文基于 3-SPRP并联机构设计了一种具备轻质高刚性能的穿戴式三支链六自由度并联骨折外固定支架，开展了运动学建模、静刚度理论建模、软件仿真验证和多目标优化设计等研究，全文结论如下.

(1) 通过闭环矢量法建立 3-SPRP并联机构位置逆解模型，基于瞬时旋量建立运动/力映射模型，为静刚度理论建模奠定基础.

(2) 建立各零部件参考坐标系，采用半解析建模法得到3-SPRP并联机构整机刚度模型；在给定6个测点位姿下比对各向线刚度的理论模型值与有限元仿真值，满足误差在 20%之内，验证刚度理论模型的有效性，为多目标优化设计提供理论模型.

(3) 以瞬时变形能在给定工作空间的均值和整机质量为优化目标，以 z向线刚度为性能约束条件，借助粒子群优化算法开展基于 Pareto前沿的多目标优化设计，根据最小距离的目标匹配原则得到最优截面设计参数，为后续物理样机开发和实验工作提供理论依据.优化后，三支链并联外固定支架质量仅增加24g，各向线/角刚度值普遍提升了50%左右.