基于三SCC结构的LCCC-S型IPT系统设计
2023-03-15林学伟杨金明钦超
林学伟,杨金明,钦超
(华南理工大学 电力学院,广东 广州 510641)
无线电能传输(wireless power transfer,WPT)是由Nikola Tesla在19世纪所提出的概念[1]。作为一种非接触式电能传输(contactless power transfer,CPT)技术,WPT技术解放了负载对于电源的导线束缚,实现了电源的便捷和安全接入。WPT的形式主要为磁场耦合、电场耦合、微波辐射等[2]。其中,磁场耦合式感应电能传输(inductive power transfer,IPT)技术已经得到了较大的发展,被广泛应用于移动电子设备、智能家居、医疗设备、工业机器人、水下探测设备、交通和航空航天等领域[3-7]。
磁耦合式IPT主要依靠发射端与接收端之间的耦合线圈进行能量传递,线圈之间的松耦合系数往往很小,而且在传输能量的过程中会产生无功功率。为减少系统中的无功损耗,提高传输效率,国内外的许多专家学者研究了许多不同的补偿网络,其中包括常见的SS、SP、PS、PP型补偿方式(S、P分别表示补偿电容为串联、并联方式),还有LCL型、CLC型、电容阵列等更多高阶的拓扑结构[8-14]。例如文献[11]对LCC拓扑进行了研究,证明在耦合系数变化范围为200%以内,系统传输功率下降不超过20%;文献[12]通过变静态补偿法,使得LCL-LCL型IPT系统具有恒压或者恒流的输出特性;文献[13]分析了基于LCL-S/LCL补偿拓扑,利用开关切换的方法实现接收端恒压或者恒流输出(与负载无关)的输出。仅使用某种谐振补偿网络或者配合开关来切换不同的拓扑,通常只能够实现恒压、恒流的特性,而无法动态调节输出功率。文献[14]在LCC拓扑的基础上,通过对逆变电路的移相控制实现输出功率的调节,但对于轻载状态下的IPT系统无法进行输出功率调节。同时,随着逆变控制角的减小,输入谐波增大,容易对器件产生损害[15]。
本研究提出基于三SCC结构的LCCC-S型拓扑,通过移相控制各金属氧化物半导体(metal oxide semiconductor,MOS)管的脉冲宽度调制(pulse width modulation,PWM)驱动信号,最终实现输出电压的无级调节。同时,还分析了三SCC电路的工作模态以及参数设计,所提出的谐振拓扑能够实现全桥开关和三SCC的零电压开关(zero voltage switching,ZVS),有效降低IPT系统中的开关损耗与无功损耗。最后通过仿真与小功率样机实验验证该IPT系统的可行性与有效性。
1 数学模型分析
1.1 LCC-S拓扑的数学模型

图1 LCC-S的等效电路
LCC-S拓扑的谐振条件为
(1)
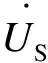
(2)
当接收端的全桥负载电阻为RL时,其等效交流负载Req、折算至发射端的反射阻抗Zre分别为:
(3)
(4)
在此谐振条件下逆变后的发射端输入电流
(5)
同时,IPT系统的输入功率Pin、输出功率Po的表达式分别为:
(6)
(7)
由式(1)不难看出,线圈、电感等感性元件和电容的取值存在一一对应的关系。当补偿网络的参数满足谐振条件时,LCC-S拓扑的输出功率Po主要受互感值M、负载电阻Req、输入电压US和补偿参数a控制;所以,对于给定规格的无线充电线圈而言,其自感LT为定值,当补偿参数a变化时,其电感值、电容值在设计上都要发生改变,不利于拓扑参数的调整。
1.2 LCCC-S拓扑的数学模型
与LCL拓扑拓展到LCC拓扑类似,改进型LCC拓扑则是在LCC拓扑的输入支路上再加入1个电容器CT1(电容值为CT1),称之为LCCC-S拓扑。LCCC-S拓扑的等效电路如图2所示,图中电容器CT2(电容值为CT2)同LCC-S拓扑中的CT。
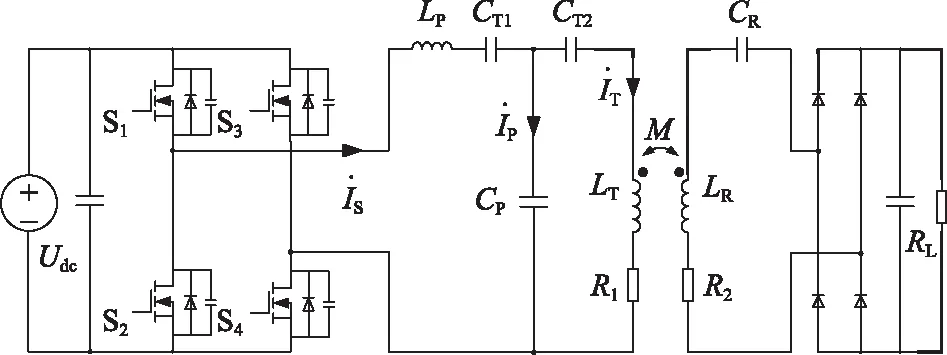
图2 LCCC-S的等效电路
对图2所示电路列写电路方程
(8)
其中
考虑到CT1和CT2在与电感和线圈串联时,其等效电路模型可以化简为LCL拓扑,如图3所示,图中L′1对应LP与CT1串联的等效电感,L′T对应LT与CT2串联的等效电感。
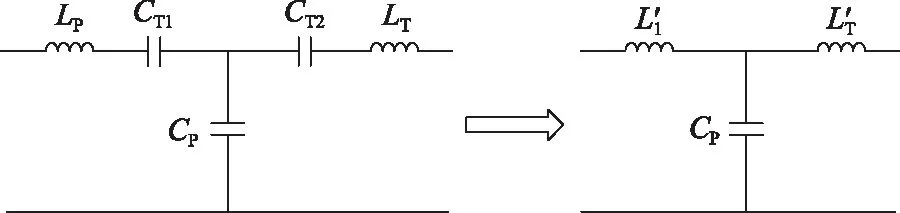
图3 简化后的LCCC-S拓扑
LCL的谐振条件之一就是必须满足L′1=L′T,
因此在参数设计上引入相同的电容CT和电感LP更容易满足谐振条件,同时也降低了下文可控开关电容(switch-controlled capacitor,SCC)移相控制的参数设计难度。
所以令
(9)
则各支路电流表达式可化简为:
(10)
(11)
(12)
为使系统的整体无功为0,谐振条件应满足:
(13)
因此各支路电流表达式(10)—(12)可进一步化简为:
(14)
(15)
(16)
由式(14)—(16)可知,当拓扑各元件参数满足条件式(9)、(13)时,输入电流IS与输入电压US同相位,线圈电流IT滞后IS四分之一周期,且与负载无关,而IP始终超前于输入电流,且与电容CP、负载、系统的谐振频率成反比。
此时系统的Pin、Po、传输效率η表达式分别为:
(17)
(18)
(19)
不同参数下的输出功率、效率曲线如图4所示,显然LCC-S拓扑的输出功率Po主要受互感值M、负载电阻Req、输入电压US和电容CP影响,而传输效率与储能元件的参数无关。

图4 不同参数下的输出功率曲线与效率曲线
同样在线圈自感LT已经确定的情况下,由于多引入了1个电容,系统的补偿方程组中便存在1个自由度,即电容CP、CT的取值并不唯一。仅改变电容值CP、CT,无需改变电感LP便可以直接在交流回路中进行输出的动态调节。
2 LCCC-S的电容控制策略
2.1 高频开关电容变换器
SCC是利用高频开关器件调节电容储能过程的结构,在交直流电路中有广泛的应用[17-19]。在AC电路中,SCC可利用PWM移相调制或者占空比调制,改变其对外的等效电容值,进而改变输出电流。SCC拓扑大致可分为半波型和全波形,其中全波型不存在单侧偏置问题,更适用于对称结构下的交流谐振网络。
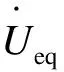

图5 全波串联型SCC
设定逆变驱动信号Vgs1的上升沿正处于初始时刻(t0),且谐振频率与逆变器工作频率一致。为不失一般性,可设该系统的输入电压us(t)、某一SCC所在支路电流iX(t)的时域基波表达式分别为:
uS(t)=USsinωt,
(20)
iX(t)=ωCeqUeqsin(ωt+φ).
(21)
式中t为时间。
SCC电路的电压与电流波形如图6所示,图中Vgs1、VgsB分别为逆变器MOS管S1、SCC电路的MOS管SB的PWM驱动信号,θ为电容器每半周内的实际充放电时间,φ为电流与输入电压之间的相位差,ψ为支路电流iX超前驱动信号VgsB上升沿的相位,α为PWM驱动信号控制角。

图6 移相调制下的SCC电路工作波形
假设开关管SB的PWM驱动信号VgsB相对输入电压US移相α,则在SB导通的时间段内,
(22)
结合图6分析各波形相位之间的关系,可得出θ、ψ的表达式分别为:
(23)
(24)
消去多余项,可得等效电容
(25)
由上述理论分析可知,该SCC模型能够实现电容的平滑调控,ψ的调节范围为[90°,180°]。同时可得MOS管实现ZVS软开关所需满足的条件为
α+φ<π.
(26)
2.2 三SCC拓扑的参数分析
SCC电路的主要组成部分是1个并联电容器和1对背靠背MOS管,需要选取适当的电容值参数,并分析SCC等效电容Ceq中主相位ψ的控制方法,以保证三SCC电路的可靠性。
三SCC拓扑等效交流电路如图7所示,图中SC至SF亦为MOS管开关,用SCC1、SCC2、SCC3取代原LCCC-S电路中的电容器CP、CT1、CT2,其对应的并联电容C1、C2、C3容值均为C。CB为SCC1所在支路的基准电容,可使得该支路的电容值存在最小值,避免发生短路。
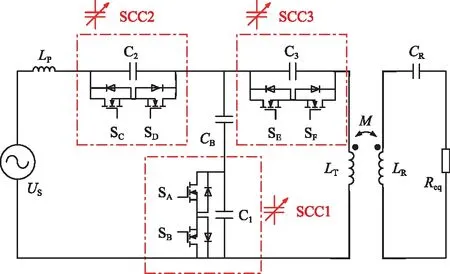
图7 三SCC拓扑等效交流电路
将式(23)、(25)代入谐振条件式(13)中,得到
(27)
式中:ψ1为SCC1支路的主相位;ψ2为SCC2支路的主相位。
在给定电感参数的情况下,SCC电路中并联电容的取值不同,其所具备的电压调节范围也不同。采用赋值法,将
(28)
代入到式(27)中,此时,将式(27)看作是关于自变量CB与C的二元函数式
(29)
则满足fA(CB,C)=0的非零解集,均为电容的可取值。此时接收端输出电压增益
(30)
图8所示为不同电容取值下的输出电压增益。由图8可知,在主相位ψ1=90°时,电压增益Gv为最小值0.4。这是由于电容器C2与C3都被交替工作的MOS管所短路,电路退化为LCL拓扑。而在不同电容比值CB/C下,不同的主相位ψ1可以对电压增益Gv进行单调调节。

图8 移相控制的电压增益曲线
同一控制角下的电容比值CB/C越高,SCC电路所具有的调控范围就越宽;然而,随着CB/C的增大,MOS管所承受的电压应力也越大,SCC1峰值电压如图9所示。导通损耗也会随并联电容C的减小而增加,因此选取电容值时,要综合考虑所需的调压范围以及MOS管耐压和效率的要求,在满足硬件输出要求的情况下,选取较大的CB/C,以获得更宽的调压范围。
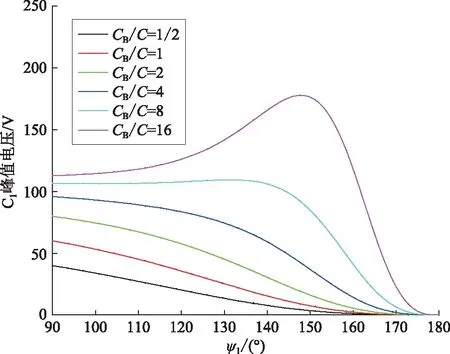
图9 移相控制的SCC峰值电压曲线
线圈电流IT滞后输入电流IS四分之一周期,在电路满足谐振条件后,IT和IS与输入电压US之间的相位差总是不变的;因此,对于SCC2支路,其开关管SD的控制角α=ψ2,输入电压US与输入电流IS的相位差恒为0。
对于SCC3支路,其开关管SF的控制角α=ψ2+90°,输入电压US与线圈电流IT的相位差恒为90°;因此,只要解决了SCC1主相位ψ1的控制方式,那么剩余SCC支路的α均可以由式(27)确定。
而对于SCC1支路的控制角控制,可假设电路运行于理想状态下,则由式(16)、(25)可得电流IP与输入电压US之间相位差
(31)
结合本研究仿真与实验的元件参数与式(23),可以得到控制角α与主相位ψ1、相位差φ之间的关系,如图10所示。

图10 α、ψ1、φ相位图
利用线性拟合的方法可以得知,在该系统中,虽然α与ψ1存在非线性关系,但这2组相位的拟合优度R2=0.997 643 27,近似线性相关。为抵消样本数量影响,调整后的R2=0.997 632 51,这说明回归直线对观测值(α,ψ1)的拟合程度高。由此,可近似认为主相位ψ1仅受α的单调线性控制,并且一一对应。这不仅避免了对相位差φ的测量,同时因α是由MOS管驱动信号直接产生的,也更容易实现对主相位ψ1的控制。
逆变器移相控制和SCC移相控制在调压的机理上有所不同。逆变器移相控制是通过改变输入方波信号的基波分量,进而改变输出的电压;而SCC移相电路是改变补偿网络的对外等效参数进行调压。SCC电路的优势如下。
a)可以改变补偿网络的参数进行重新设置。线圈老化、电感或电容的实际阻抗与标称值存在误差,都将导致系统不满足谐振条件,造成传输效率下降;SCC电路可以灵活调节其控制角,使得补偿网络参数匹配相应的谐振条件。
b)SCC电路在原边工作频率的选择上更加灵活。逆变器直接移相只能适用于特定频率下的IPT系统调节,一旦发生频率偏移,系统不满足谐振条件,其输出效率会下降;而SCC移相电路是改变补偿网络参数,因此IPT系统可以工作在多个频率点下,并且依然满足谐振条件。系统输入、输出波形如图11所示,当系统工作在90 kHz时,可以调节输入电压、电流呈零相角(zero phase angle,ZPA),其工作状态依然满足谐振条件。图11中Uout为输出电压(直流负载两端电压),Iout为流过直流负载的输出电流。
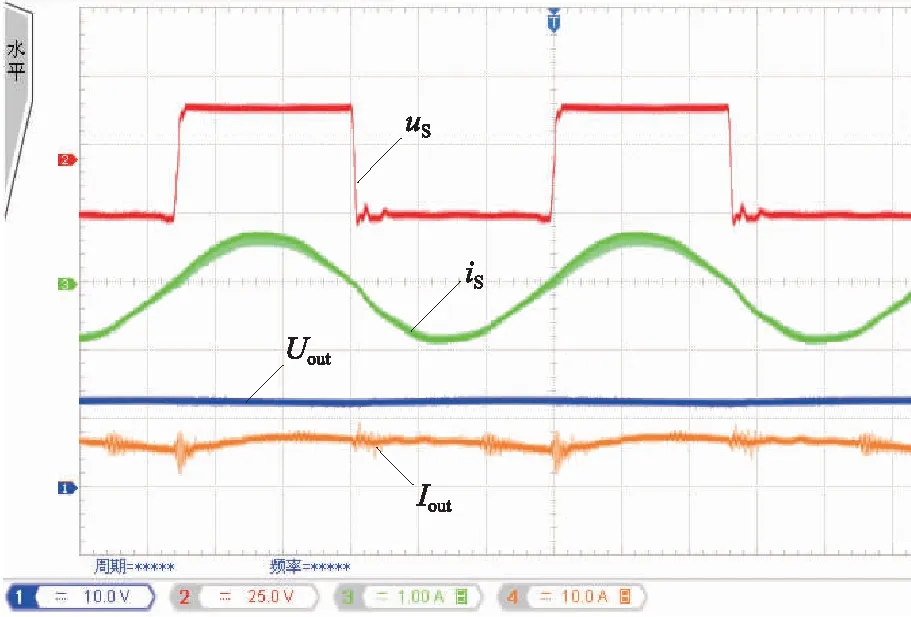
图11 90 kHz时输入、输出波形
c)当系统降频的时候,IPT系统会呈容性。此时电流超前于电压,这不利于逆变器(尤其是基于移相控制的逆变器滞后桥臂[20])ZVS的实现,同时会使开关噪声增大;而SCC电路在一定频率范围内都可以使IPT系统略呈感性。
2.3 三SCC电路的工作模态分析
同样设定逆变驱动信号Vgs1的上升沿正处于初始时刻(t0),三SCC电路各支路工作周期如图12所示。

图12 三SCC工作周期分析
在图12中:VgsX对应高频开关管SX的驱动信号,其中X∈{1,B,D,F};ICA(Y)、IQ(Y)、ueq(Y)分别为各SCC的流经并联电容器的电流、MOS管漏源电流、两端等效电压,其中Y∈{C1,C2,C3},对应3个SCC。
各支路电流关系为:
(32)
1个工作周期内各个MOS管的占空比均为50%,3个SCC的工作模态可以根据MOS管的导通状态,分为6种不同的工作周期,三SCC工作模态如图13所示,其中流经SCC1的绿色线为IP,流经SCC2的红色线为IS,流经SCC3的黄色线为IT。

图13 单周期三SCC工作模态
a)[t0,t1)段:初始输入电流IS为正。SA、SC、SF分别导通,此时电路处于模态1。电容C2两侧的电压无法突变且为左负右正,C1、C3由于各自MOS管的导通而被钳制在零电位。
b)[t1,t2)段:SF关断,SE导通,此时电路处于模态2。IP为充电电流且不断减小,C3两端电容电压反向增大。
c)[t2,t3)段:SA关断,SB导通,此时电路处于模态3。IP为充电电流并且不断减小,C1两端电容电压反向增大;电容C2放电结束,输入电流IS流经SC;当电流IT过零点后,C3两端电压开始减小。
d)[t3,t4)段:SC关断,SD导通,此时电路处于模态4。输入电流方向依然为正,并向C2充电;电流IT、IS先后经历过零点,即电流换向,电容C1由充电转为放电阶段。
e)[t4,t5)段:SE关断,SF导通,此时电路处于模态5。C3从零电位位开始充电,C1放电结束并被MOS管SB的导通所钳位。
f)[t5,t6)段:SB关断,SA导通,此时电路处于模态6。电容C1从零电位开始反向充电,C2放电结束并因MOS管SD的导通而被钳位在零电位,C3电流换向并开始放电。
g)[t6,t7)段:SD关断,SC导通,此时电路回到模态1。而初始时刻t6电路的开关状态虽为SA、SC、SF导通,但其电特性尚未恢复,C2从零电位开始反向充电,C1开始放电。
h)当C2因电流过零点开始放电,C1放电结束后,在t7时刻各开关状态与电特性才与t0时刻的相同。
在t0—t7内,三SCC电路完成了1次工作模态上的循环,MOS管开关频率与系统谐振工作频率相同。
由上述模态分析可以看出,不同支路的SCC都存在电容充放电的过程,而且不同的充放电时间导致电容储存的电荷数量不同,进而改变各支路SCC等效电容值。即使已给定MOS管触发信号,但在并联电容完成放电之前,MOS管皆无法导通,直至电容放电完成。此时两端电压为0,即MOS管可以零电压导通,ZVS软开关得以实现。
3 仿真与实验分析
3.1 仿真与结果分析
利用PSIM仿真软件对提出的三SCC结构的LCCC-S型IPT系统进行仿真验证。系统的工作频率f为100 kHz,各SCC电路的并联电容值C相同。仿真中还考虑了MOS管的导通电阻Rds、反并联体二极管的正向压降(反映其导通损耗),以及电感元件的直流电阻RDL(反映其功率损耗),同时,通过多次试验校准了α的调节范围,对应主相位ψ1的调节范围[90°,180°]。
具体仿真参数设置见表1。

表1 三SCC仿真电路参数
结合绘图工具Origin重新绘制得到仿真波形,部分波形如图14所示,C1的控制角α=79.2°,输入电压uS的过零点超前于输入电流iS的过零点,经整流后的输出电压Uout为50.51 V,USA、USB分别为MOS管SA、SB两端的漏源电压。

图14 IPT系统的部分仿真波形
图15所示为SCC1电路MOS管SA的驱动信号VgsA与SA的漏源电压USA的波形对比。由图15可知:电容电压无法突变,故只有当并联电容C1彻底放完电后,MOS管两端的漏源电压从0转为正电压;MOS关断期间并联电容的充放电时间θ小于系统的半工作周期,此时MOS管导通的瞬间两端电压为0,从而实现了SCC中零电压导通。

图15 SCC拓扑的仿真波形
对于全桥逆变器,只要保证逆变后的系统输入阻抗略呈感性,即输入电压uS超前于输入电流iS,便可实现全桥开关的ZVS导通[21]。
3.2 样机实验结果分析
本研究设计了含三SCC拓扑的高阶IPT系统,实验主要参数选择与仿真参数一致。实验样机由直流电源、辅助电源、逆变器、SCC、磁耦合线圈、接收端补偿电路、整流电路和直流电子负载等组成。由数字信号处理器DSP28335产生共4对互补的PWM驱动信号,经由光耦HCPL-3140隔离驱动逆变器、3个SCC中的MOS管。搭建实验样机如图16所示。

图16 实验样机
图17所示为SCC的调压波形图。输入电压uS保持不变,通过改变SCC各自的移相控制角,使得输出电压Uout从35 V跳变至25 V,实现对输出电压的动态调节。得益于CT1=CT2这一谐振条件,无论输出为35 V还是25 V,VgsE信号始终超前VgsD信号90°的相位,与前文的分析一致。
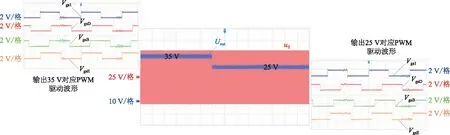
图17 SCC移相调压波形(35 V至25 V)
图18、19所示为IPT实验样机在互感M=27.6 μH时,不同负载下的各种电压、电流波形。
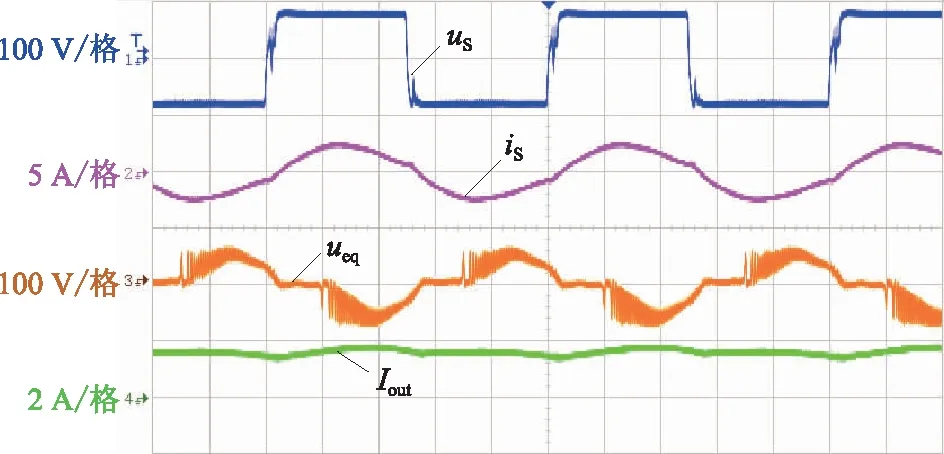
图18 负载为30 Ω实验波形(M=27.6 μH)
图20所示为IPT实验样机在互感M=18.4 μH时,负载为20 Ω下的电压、电流波形。将实验波形与仿真波形图14进行对比分析,二者波形形状基本一致。
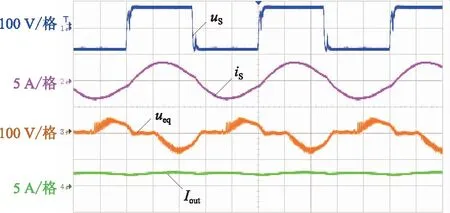
图19 负载为20 Ω实验波形(M=27.6 μH)

图20 负载为20 Ω实验波形(M=18.4 μH)
由图18—20可知,输入电流略滞后于输入电压,系统呈弱感性,无功损耗较小。同时,通过调节α可以实现输出电压的调节。对于不同的直流负载RL以及不同的互感M情况,可以通过调整发射端SCC的PWM驱动信号控制角α,使得输出电压Uout满足负载需求。
a)当RL=30 Ω、M=27.6 μH时,调整α=68.4°,可以控制输出电压Uout=50.01 V(要求输出50 V),输出电流Iout=1.67 A。
b)当RL=20 Ω、M=27.6 μH时,调整α=73.7°,可以控制输出电压Uout=50.05 V(要求输出50 V),输出电流Iout=2.50 A。
c)当RL=20 Ω、M=18.4 μH时,调整α=77.8°,可以控制输出电压Uout=40.07 V(要求输出40 V),输出电流Iout=2.00 A。
对于SCC电路的ZVS验证如图21所示。图21展示了MOS管的PWM驱动信号VgsA、漏源电压USA和电流IQ(C1)的实验波形,其零电压导通区域也已圈出。不难看出在MOS管施加驱动信号的瞬间,漏源电压USA为0,并且需要等电容完成1次充放电过程,漏源电流IQ(C1)才会正向流经MOS管。这就是零电压导通的全过程。

图21 MOS管驱动信号、漏源电压和漏源电流波形
不同主相位ψ1的效率曲线如图22所示,计算效率时所用的输入功率为直流电源输出电压与输出电流的乘积。仿真效率最高为92.96%,整体效率维持在91.51%;实验最高效率为83.43%,整体效率维持在80.60%。系统的传输效率在MOS管控制角的变化范围内保持稳定,说明不同状态下的SCC开关损耗保持一致。

图22 移相调制的效率曲线
仿真效率与实验效率之间存在10%左右偏差,其主要损耗源于实验中的振铃现象与线路损耗,可通过改进PCB布线设计等改善。
设定负载RL=20 Ω,互感M=27.6 μH,输出电压曲线如图23所示,其中包含了理论计算输出电压曲线、仿真曲线、实验曲线。
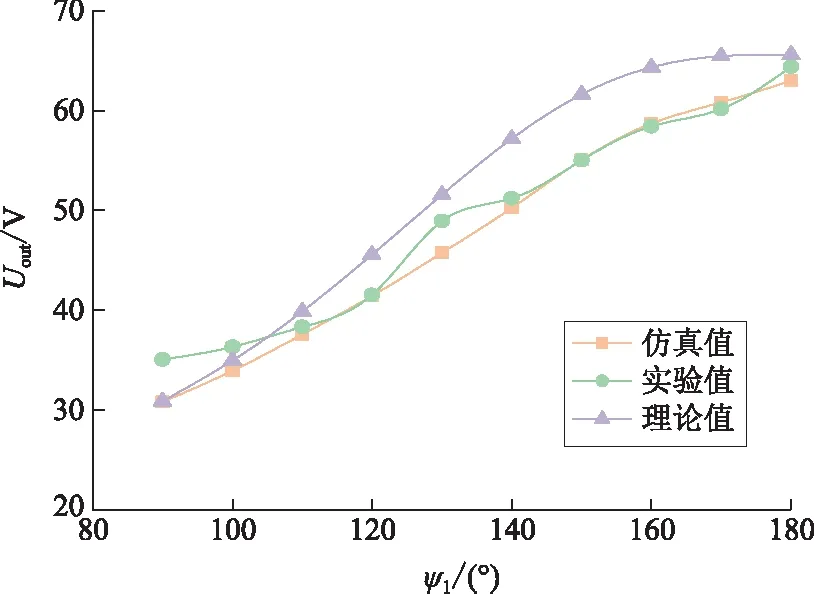
图23 移相调制的输出电压曲线
由于采用了线性拟合的控制方法,相同控制角α下的实验输出电压与理论值存在一定偏差,但三者的输出调压范围与电压变化趋势大致相同;因此,可以通过重新调节α,使得输出电压保持一致。当α的精度足够高时,系统可以进行输出电压平滑调整,即实现无级调节。
从实验结果可以看出,三SCC结构的LCCC-S型IPT系统可以实现全桥开关和SCC开关管的ZVS,在不同负载、互感的条件下,通过PWM移相调制可以实现接收端输出电压的平滑控制,具有一定的可行性和有效性。
4 结论
本研究通过引入SCC拓扑,结合固定元器件参数下的LCCC电路,建立了三SCC结构的LCCC-S型IPT系统,并对相应参数设计与工作模式进行了数学分析。
具体总结如下:
a)该IPT系统可以实现全桥开关和SCC开关的ZVS软开关,有较小的无功损耗。在保持系统传输高效率的同时,还可以对不同条件下的输出电压进行无级调节。
b)三SCC拓扑的控制方式简化为PWM的移相控制,无需外加过零检测电路来完成相位差的校准,具有与理论值相同的调压范围与变化趋势,易于控制。后续拟采用采样通信的方式搭建控制闭环,进一步验证三SCC拓扑在动态IPT系统中的可行性。
c)仿真与设计的实验样机都证明了简化后的移相控制对三SCC电路实现电压调节的可行性。但由于实验所设计PCB板的连接导线较多、较长,导致电容充放电时发生振铃现象,降低了实验的传输效率。后续将采用更加合理的PCB板布局来进行实验验证,进一步提升实验效率。
