钢管混凝土框架-屈曲约束支撑结构概率地震易损性评估研究

王静峰，李贝贝，王元清，李国强

钢管混凝土框架-屈曲约束支撑结构概率地震易损性评估研究

王静峰1, 2，李贝贝1, 3，王元清3，李国强1, 2

(1.合肥工业大学土木与水利工程学院，合肥 230009；2.合肥工业大学土木工程结构与材料安徽省重点实验室，合肥 230009；3.清华大学土木工程安全与耐久教育部重点实验室，北京 100084)

为了研究钢管混凝土(CFST)框架-屈曲约束支撑(BRB)结构的抗震性能以及地震动持时对结构概率地震易损性的影响，基于能量平衡的塑性设计方法，设计了9层框架支撑结构．选取其中一榀单层单跨的框架支撑试件进行了低周循环加载试验和数值分析．采用OpenSees程序建立了9层典型三跨子结构的弹塑性分析模型；通过增量动力分析法得到了结构在不同工程需求参数和地震动强度参数下的易损性曲线，分析了地震动持时对结构抗震性能的影响．研究结果表明：试件的水平荷载-位移滞回曲线饱满，耗能稳定；结构90%的塑性变形耗能集中于屈曲约束支撑；整体损伤因子(ODI)可以较好地反映地震动持时对框架支撑结构累积损伤的影响；长持时地震动下结构的倒塌中位值比短持时的低24%．以ODI为工程需求参数时，考虑地震动谱加速度和重要持时的地震动强度综合指标NP-D表现出更优的实用性、有效性、充分性和调幅鲁棒性．对于NP-D，罕遇地震水平下，长持时地震动下的ODI超越0.2和0.4限值的概率分别是短持时的1.74和5.0倍，因此建议钢管混凝土框架-屈曲约束支撑结构的抗震设计和分析应关注地震动持时对结构累积损伤的影响．

地震动持时；钢管混凝土框架；屈曲约束支撑；易损性曲线；损伤因子

钢-混凝土组合结构是在钢结构和混凝土结构基础上发展起来的一种新型结构形式，具有施工性能较优、综合效益高等优点[1]．为了提高钢管混凝土框架结构在高设防烈度区的抗震性能，一些学者尝试在框架中设置屈曲约束支撑，并研究了其在拟静力和拟动力作用下的抗震性能，如Tsai等[2]、贾明明等[3]、于敬海等[4]、王波等[5]、Li等[6]，试验和分析结果表明，由于屈曲约束支撑具有拉压受力近似均等和延性性能好等优点[7-10]，可以比较显著地提高结构的抗侧刚度和耗能能力，适用于高设防烈度区以应对未来可能遭遇的罕遇甚至超罕遇地震．

现行国家标准《建筑抗震设计规范》(GB50011—2010)[11]指出，时程分析选择的地震动加速度时程曲线应满足地震动三要素的要求：频谱特性、有效峰值和持续时间(简称持时)．关于持时，仅说明地震加速度时程曲线的有效持时为结构基本周期的5～10倍．然而，依据该规范选取的地震动持时一般不持久，可能无法有效反映结构在长持时地震动作用下的累积损伤而引起结构的破坏．2010年的智利摩尔8.8级地震和2011年的日本东北部9.0级地震导致大量的建筑和桥梁结构发生严重损伤破坏；地震台站记录的地震动持时明显高于以往其他地震事件记录的地震动持时．结构在长持时地震动作用下会历经更多的加、卸载循环，刚度和强度退化更加显著．历次长持时的地震灾害引起了不少学者开始关注地震动持时对结构地震响应的影响．

地震动持时的定义分为4类：括号持时、一致持时、重要持时和有效持时．目前大多数学者采用重要持时(第3节中的式(1)和式(2))来区别长、短持时地震动．Chandramohan等[12]对5层平面钢框架和钢筋混凝土桥墩在长、短持时地震动作用下的抗倒塌性能进行了研究．Belejo等[13]通过3层不对称的空间钢筋混凝土框架结构的振动台试验和数值分析研究了地震动持时对结构的影响．Pan等[14]采用易损性曲线研究了长短持时地震动对两层木结构房屋的损伤影响．韩建平等[15]研究了长短持时地震动对5、8和10层钢筋混凝土结构易损性和抗震性能的影响．研究均表明地震动持时对结构累积损伤的影响较大，建议结构的抗震设计和分析应考虑地震动持时的影响．

自2008年汶川地震后，我国局部地区地震频发，造成了极大的生命安全和财产损失，国家和地方政府高度重视结构的抗震韧性．然而，关于地震动持时对钢管混凝土框架-屈曲约束支撑结构体系抗震性能影响的研究尚鲜见报道．因此，本文首先基于能量平衡和整体失效模式的塑性设计方法[16]，设计9层钢管混凝土框架-屈曲约束支撑结构；然后从9层结构中选取1榀单层单跨的框架支撑，缩尺后对其进行低周循环加载试验；基于试验结果，采用OpenSees[17]建立9层典型三跨子结构的弹塑性分析模型并评估结构设计的合理性；最后基于增量动力分析法(IDA)，选取合适的地震工程需求参数和地震动强度参数，建立结构的易损性曲线，分析地震动持时对结构抗震性能的影响．

1 结构设计

为了评估钢管混凝土框架-屈曲约束支撑结构体系在长短持时地震动作用下的损伤概率分布，采用基于能量平衡和整体失效模式的塑性设计方法[16]设计9层结构．平面布置见图1，跨度均为7200mm，结构端部和中间的跨中位置布置屈曲约束支撑作为抗侧力构件．考虑结构的对称性，仅选择⑤轴的3跨子结构作为研究对象．立面布置见图2，首层层高为4500mm，其余层层高为4200mm．

结构的主要设计资料：设防烈度为8度(0.2)；设计地震分组为第2组；场地类别为Ⅱ类，场地特征周期为0.40s．基本风压为0.40kN/m2；地面粗糙度为C类；基本雪压为0.30kN/m2．标准层和不上人屋面活荷载标准值分别为2.0kN/m2和0.45kN/m2；恒荷载标准值分别为3.5kN/m2和5.0kN/m2；女儿墙、外墙和内墙自重分别为2.95N/mm、2.0kN/m2和1.0kN/m2．梁、柱、节点板、支撑弹性段钢材采用Q345B，支撑耗能段钢材采用Q235B，钢管柱内填C40混凝土．

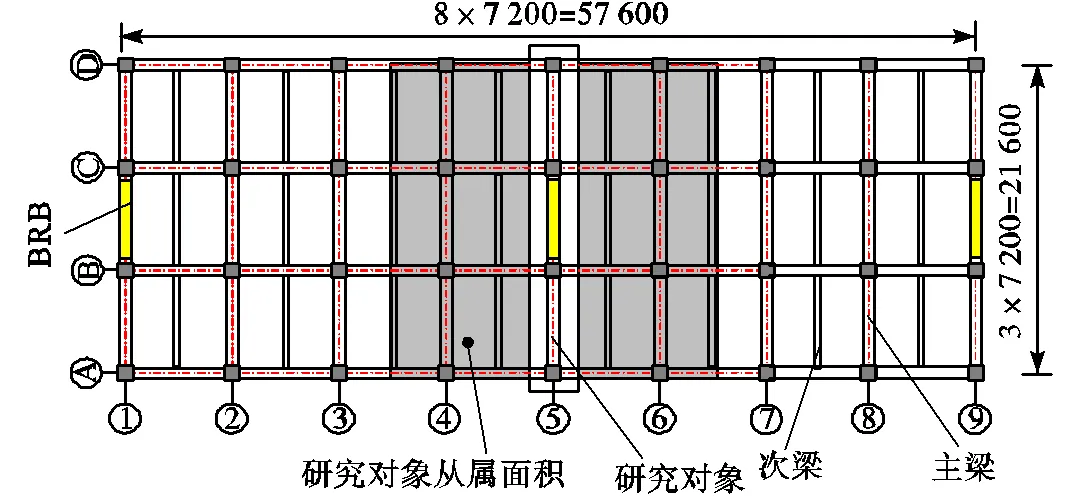
图1 结构平面布置图

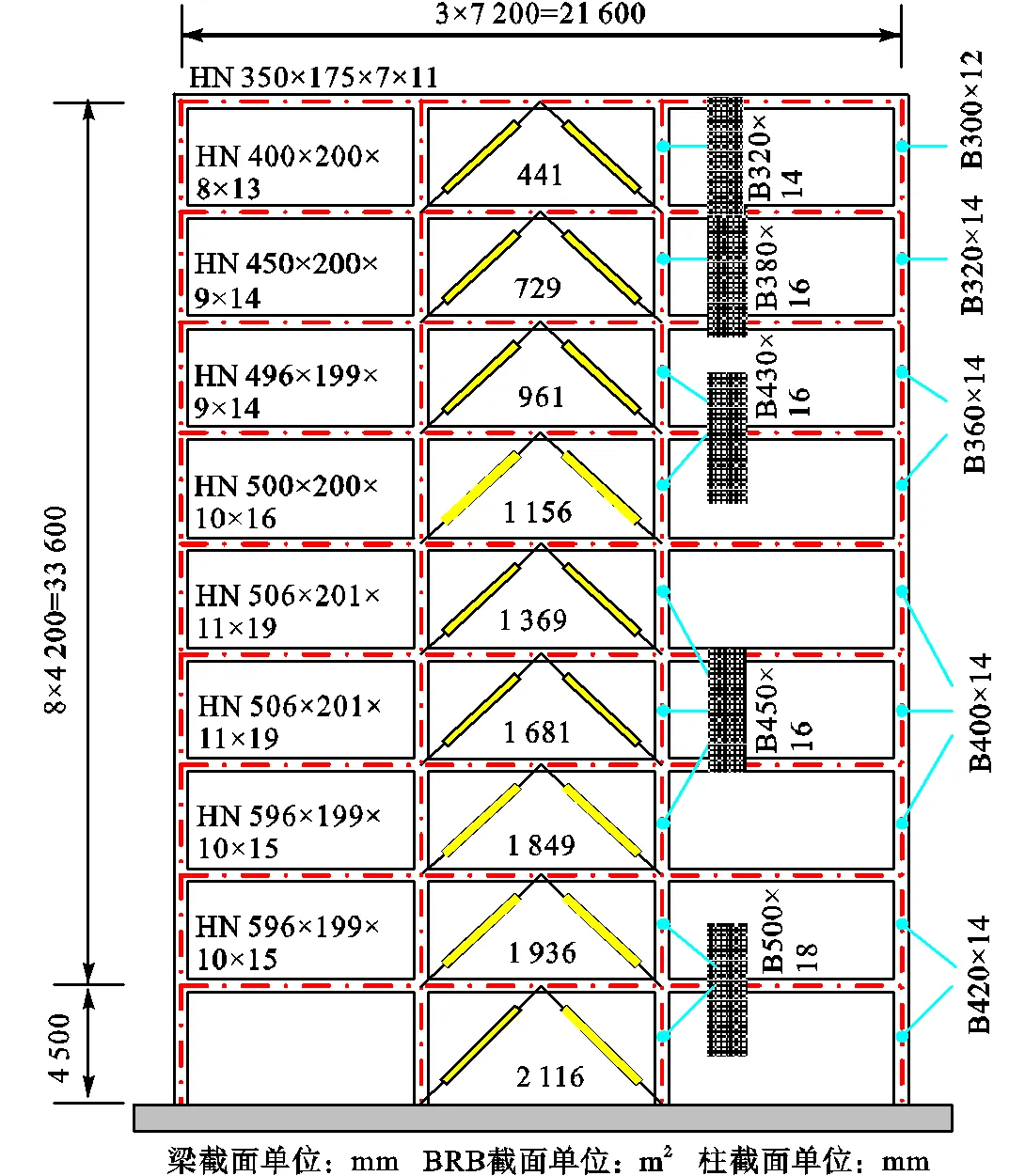
图2 结构立面布置图和构件截面尺寸

参考现行国家标准《建筑抗震设计规范》(GB50011—2010)[11]和安徽地方标准《屈曲约束支撑结构技术规程》(DB34/T5069—2017)[18]有关规定，结构在多遇、设防和罕遇地震作用下的层间位移角限值分别为0.4%、1.0%和2.0%．根据设计要求，初估梁柱截面尺寸，计算结构的重力荷载代表值和侧向力分布系数；计算结构的自振周期，以结构在设防和罕遇地震下的层间位移角限值为目标，结合能量平衡原理和整体失效模式，得到结构的设计基底剪力．根据侧向力分布系数确定沿楼层高度分布的地震作用，同时考虑-效应．假定屈曲约束支撑和框架分别承担结构总剪力的50%，可获得屈曲约束支撑芯板耗能段的截面尺寸，见图2．根据重力荷载代表值和设计地震作用在梁端和跨中产生的弯矩以及屈曲约束支撑于极限状态下在梁端产生的轴力，设计校核钢梁，钢梁尺寸见图2；钢梁的抗弯承载力沿楼层高度的分布尽量与侧向力分布系数保持一致，使得各层钢梁的转动变形趋于一致．为了保证钢管混凝土框架在目标侧移下达到整体屈服受力模式，应避免其他不利的薄弱层失效模式．根据水平地震作用和-效应，对框架所做的外力功与框架柱脚、梁柱节点塑性转动产生的内力功相等的原则，建立整体屈服和薄弱层失效模式下的等效屈服机制直线，据此设计校核钢管混凝土柱，设计结果见图2．详细的塑性设计方法和流程见文献[16]．

2 钢管混凝土框架-屈曲约束支撑结构试验与数值分析

2.1 试验方案

为了研究钢管混凝土框架-屈曲约束支撑结构的抗震性能，本文对一榀单层单跨试件进行了低周循环加载试验，见图3．根据实验室条件，以近似1∶2的缩尺比例从原结构第8层中截取试验对象．试件的跨度和高度分别为3800mm和2100mm；钢梁和方钢管柱的截面尺寸分别为HN200´100´5.5´8mm和ÿ180´8mm，屈曲约束支撑芯板耗能段的截面尺寸为25´25mm．梁柱节点采用栓焊混合连接，支撑与框架采用销轴连接．钢材的材料性能见表1；钢管柱内混凝土的28天立方体抗压强度和弹性模量分别为52.14MPa和26896MPa．

采用位移控制对试件进行加载，加载制度见表2，y为试件的预估屈服位移，取10mm．加载装置见图3(a)，柱顶施加0.3倍的柱轴压承载力．

2.2 试验结果与数值分析

由于销轴间隙的存在，屈曲约束支撑芯板耗能段在层间位移角达到0.38%时屈服．层间位移角小于2.86%时，试件的水平荷载随着侧移的增加而增大，相同加载级下的水平荷载-水平位移曲线几乎重合，试件的滞回耗能饱满且稳定．层间位移角大于2.86%时，由于没有设置侧向约束，钢梁突然发生平面外失稳，钢梁端部上翼缘由于扭转发生了屈曲变形，随后发生了撕裂破坏，承载力迅速下降而停止加载，见图3(b)和(c)．

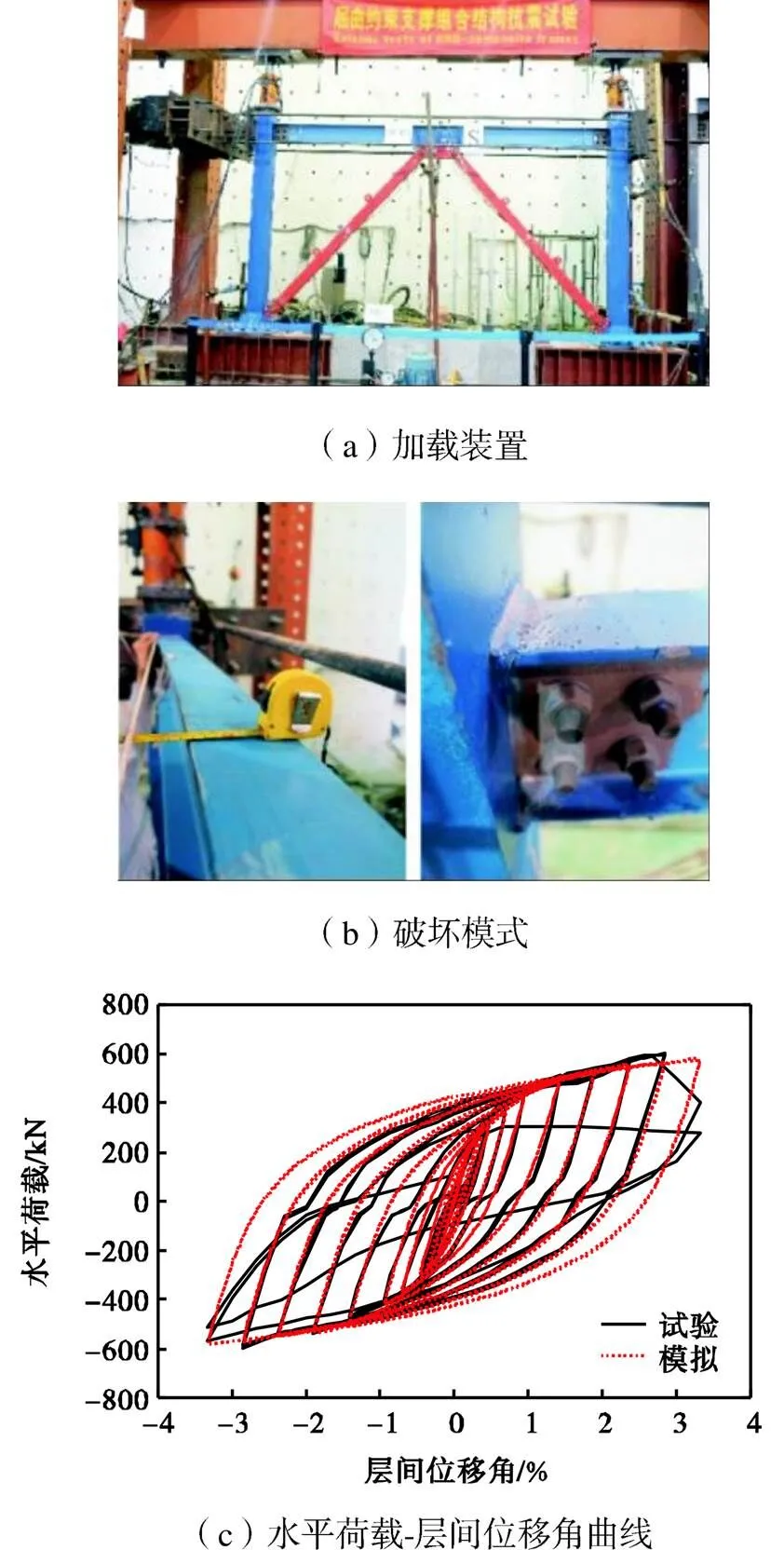
图3 钢管混凝土框架-支撑结构试验

表1 钢材材料性能

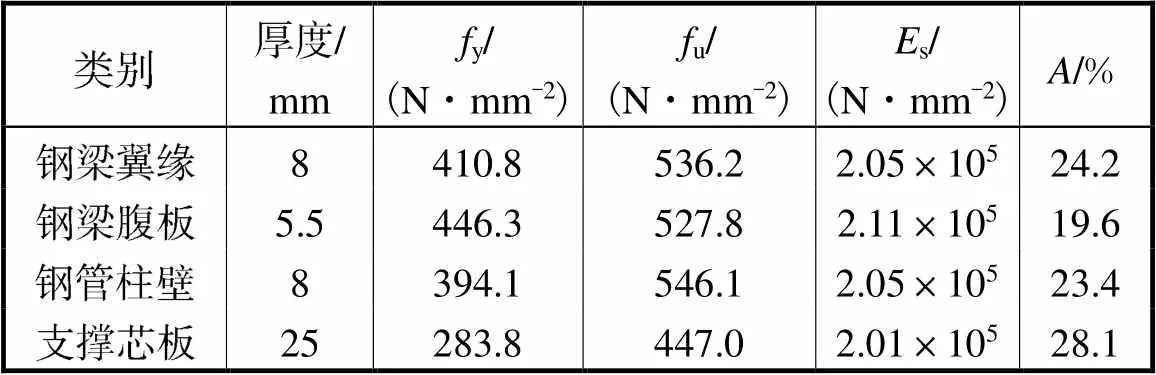
Tab.1 Material properties of steel

注：y为钢材屈服强度；u为钢材抗拉强度；s为钢材弹性模量；为钢材断后伸长率.

表2 加载制度

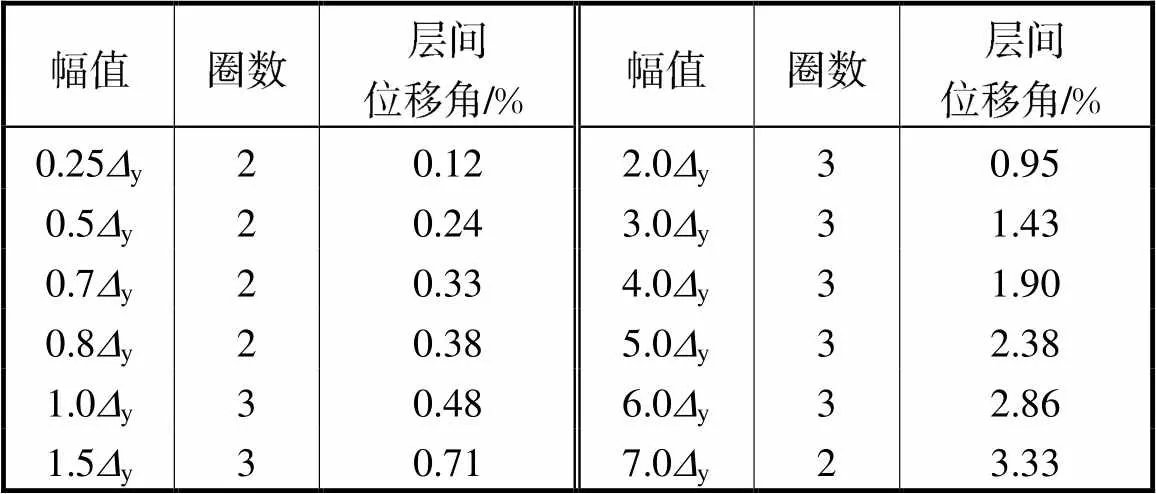
Tab.2 Loading protocol

基于试验结果，采用OpenSees程序[17]建立试件的弹塑性分析模型．钢管混凝土柱采用dispBeamColumn单元，钢梁采用elasticBeamColumn和zeroLength单元．分别采用Steel02和Concrete02材料模型模拟钢管柱和钢管内填混凝土的力学行为．考虑钢管对混凝土的约束效应，Concrete02材料模型的关键参数峰值压应力pc、峰值压应变c0、开裂压应力pcu、开裂压应变cu分别为46.28MPa、0.0027、41.58MPa和0.004[6]．将改进的Ibarra-Medina-Krawinkler模型(Bilin材料模型)赋予zeroLength单元以模拟钢梁端部的塑性损伤退化行为，该材料模型的关键参数有效屈服强度y、有效弹性刚度e、极限前的塑性转动能力p、极限后的转动能力pc、极限转动能力u和残余强度系数，其值分别为98.35kN·m、3.32´1011kN/m、0.0482、0.219、0.4和0.4[19]．此外，屈曲约束支撑采用corotTruss单元，将屈曲约束支撑芯板耗能段的面积赋予Steel4材料模型，根据轴向刚度等效原则修正Steel4材料模型的弹性模量以考虑支撑弹性段和节点板对结构的影响[6]；关键参数有支撑等效刚度0＝2.54´105kN/m，随动强化参数[20]k＝0.012、0＝22.0、1＝0.91、2＝0.15、kc＝0.022、0c＝20.0、1c＝0.89、2c＝0.02，等向强化参数[20]i＝0.003、i＝0.25、l＝0.0001、i＝3.0、yp＝1.0、ic＝0.0054、ic＝0.15、lc＝0.00038、ic＝3.0、ypc＝1.0。

上述关键参数均基于混凝土和钢材的材性试验数据计算得到．对分析模型施加与试验相同的加载制度，模拟结果见图3(c)．除最后一个加载级下由于试件发生面外失稳而承载力突变外，其余加载级下的试验与有限元的承载力、刚度和耗能误差均在5.0%以内，两者吻合较好，表明本文的弹塑性分析模型的建模方法可以用于后续9层结构的分析．

3 非线性时程分析

3.1 地震动记录选取

地震动的持时指标、筛选方法和弹塑性分析模型会对研究结果产生较大影响．目前众多学者采用重要持时5-75以区分长短持时地震动，即地震动的累积能量占总输入能量5%和75%时对应阈值之间的时间差[21]．

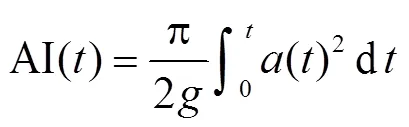
5-75＝2－1(2)

式中：()为时刻地震动的加速度；为重力加速度；2和1分别为地震动的累积能量占总输入能量的75%和5%时对应的时刻．

表3 长、短持时地震动信息

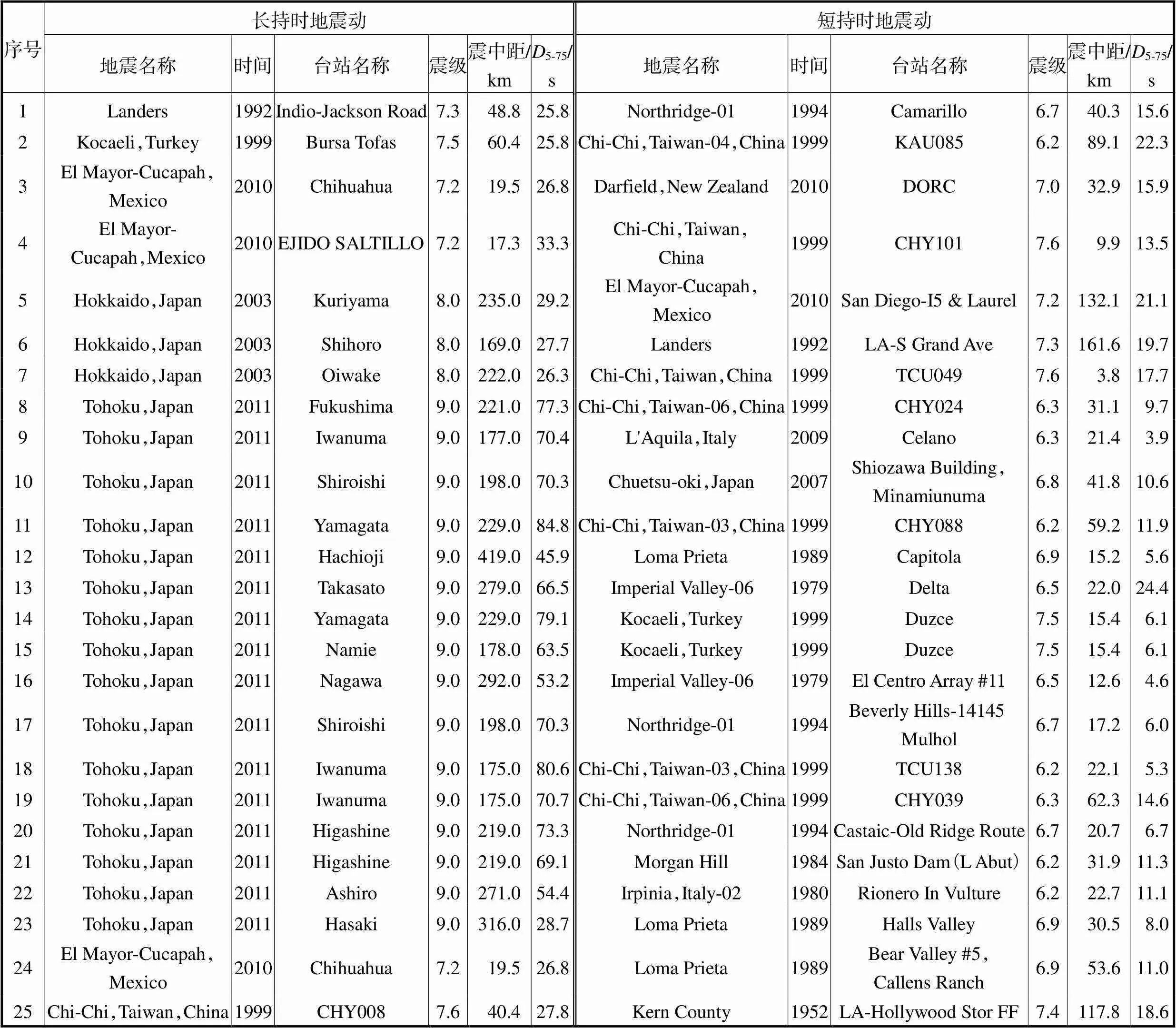
Tab.3 Information of selected long and short duration ground motions

3.2 弹塑性分析模型

综合结构的对称性和模型计算效率，采用OpenSees程序建立典型3跨钢管混凝土框架-屈曲约束支撑平面子结构的弹塑性分析模型．为使结构在地震作用下的响应具有一般性，材料强度均采用平均值．C40混凝土的变异系数取14.1%，Q235B和Q345B钢材的变异系数取9.5%和7.3%[22]．假定屈曲约束支撑tr,i/wp,i＝0.08，co,i/wp,i＝0.14，gp,i/wp,i＝0.18；tr,i/c,i＝2.0，co,i/c,i＝3.0和gp,i/c,i＝8.0；其中tr,i、co,i、gp,i和wp,i分别表示第层支撑过渡段、连接段、节点板和工作点之间的长度，tr,i、co,i、gp,i和c,i分别表示第层支撑过渡段、连接段、节点板和芯板耗能段的截面面积．

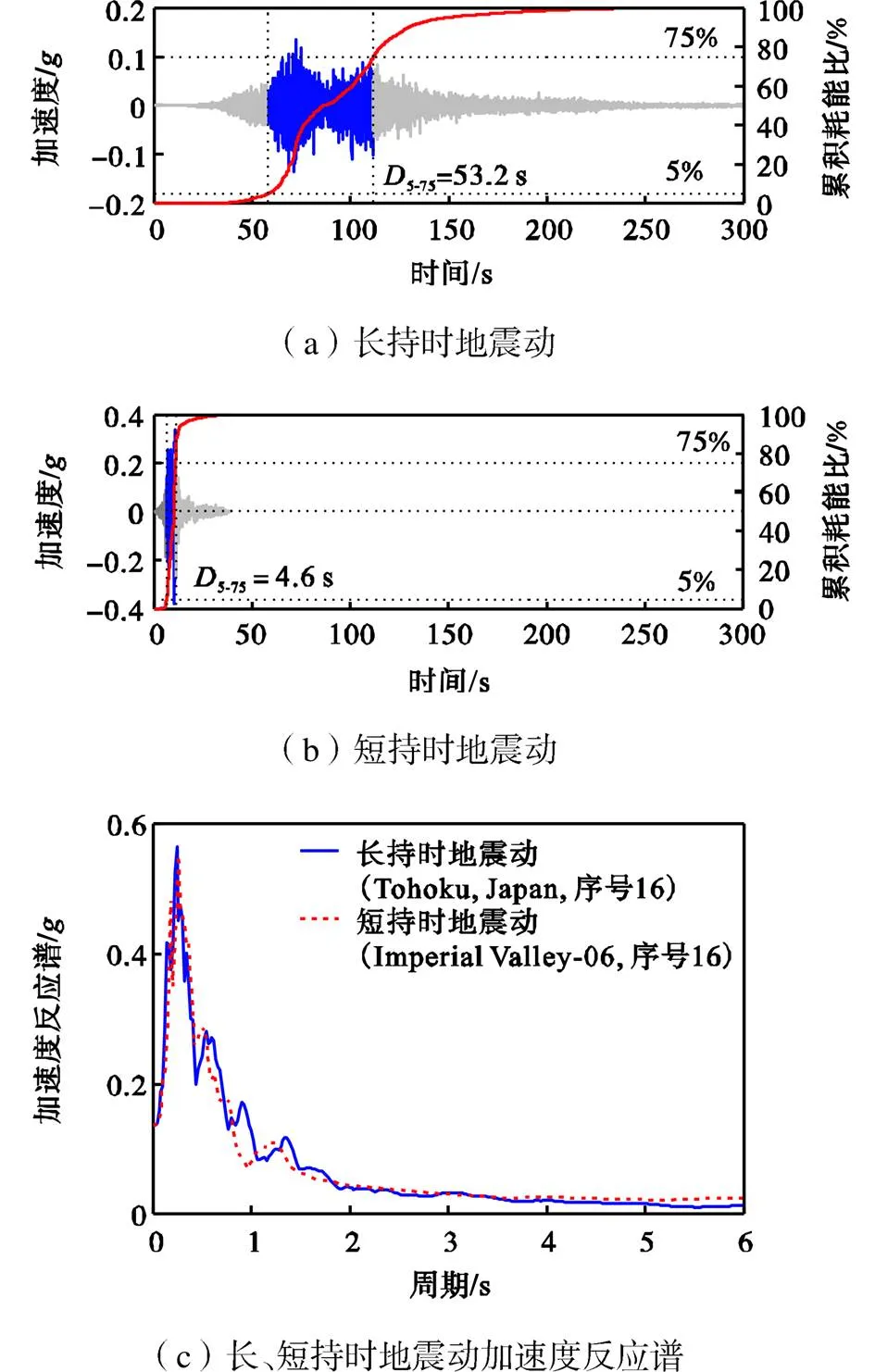
图4 长持时与等效短持时地震动的对比

典型3跨平面子结构的非线性分析模型见图5．在模型两侧设置摇摆柱以考虑子结构承担附属区域内的地震作用和-效应，摇摆柱底和每层层高位置处铰接，并通过连杆铰接于子结构上，赋予摇摆柱和连杆很大的弹性模量以实现刚性特征，此时摇摆柱只承受竖向力．构件单元类型和材料模型的选取以及关键参数的计算与上述第2节中相同．

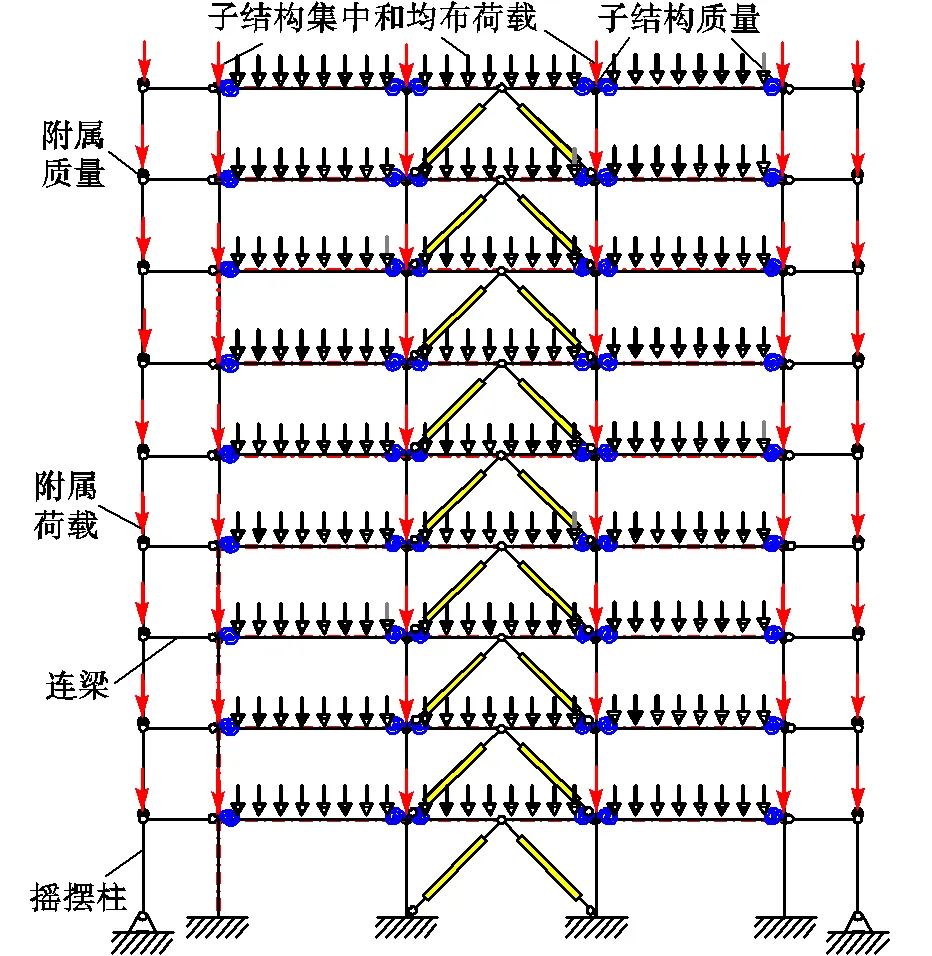
图5 非线性分析模型

3.3 非线性时程分析结果

结构的自振周期为2.04s，根据我国抗震规范[11]，将25条长持时地震动的PGA分别调至70gal、200gal和400gal，分别对应8度(0.2)设防烈度的小震、中震和大震水平．对子结构进行非线性时程分析，层间位移角响应见图6．层间位移角的平均值加标准差除了在多遇地震下的8层和9层以及罕遇地震下的3层略大于0.4%和2.0%外，其余层间位移角均小于目标值，且沿楼层高度分布比较均匀，未出现局部明显凸出现象．

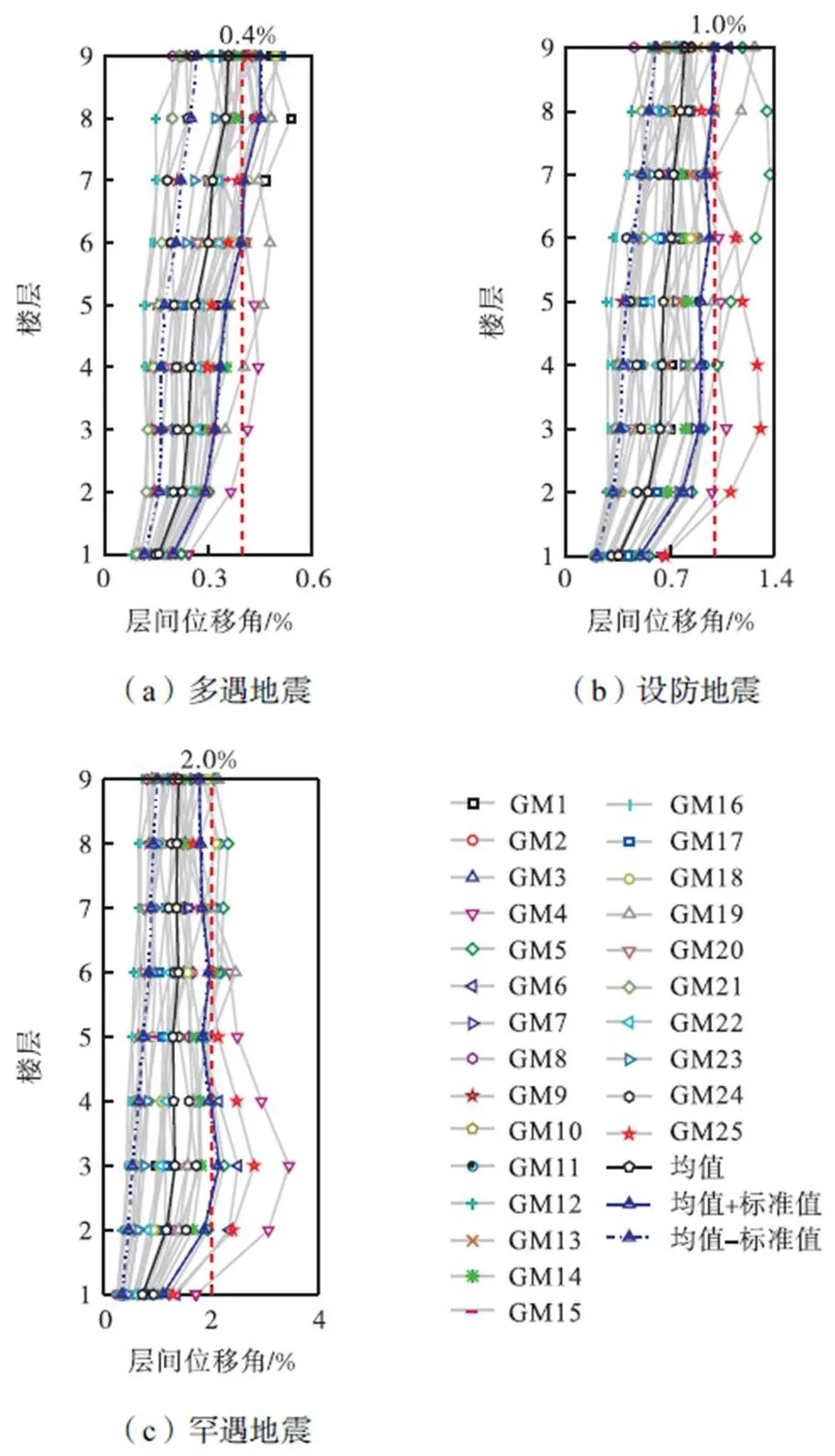
图6 结构层间位移角响应

图7给出了屈曲约束支撑和钢梁端部在设防地震(DBE)、罕遇地震(MCE)和1.5倍罕遇地震(超罕遇地震)下的耗能比(h/tot)以及层间位移响应分布，其中h/tot表示屈曲约束支撑或钢梁在一组长持时或短持时地震动作用下的累积耗能与结构总累积耗能比值的中位值．由图7可知：①结构在各地震等级作用下的塑性变形主要集中于屈曲约束支撑，所有支撑累积的h/tot在90%以上；总体上，支撑耗能沿楼层高度分布比较均匀，且长持时地震动下的h/tot基本大于短持时地震动；1～4层屈曲约束支撑的h/tot随着地震等级的增加而增大，但其增长率随着楼层的递增而逐渐减小；5～9层屈曲约束支撑的h/tot随着地震等级的增加而减小，但其增长率随着楼层的递增而逐渐增大．②钢梁端部的塑性耗能在设防和罕遇地震下的耗能很小；超罕遇地震下，长、短持时地震动的总耗能比分别为1.32%和3.40%．③结构在超罕遇地震下的层间位移角为2.0%～3.0%，且沿楼层高度分布比较均匀，未出现薄弱层，表明结构在超罕遇地震下的楼层变形仍然可控．分析表明本文设计的9层钢管混凝土框架-屈曲约束支撑结构较为合理，可以用于后续的地震易损性分析．

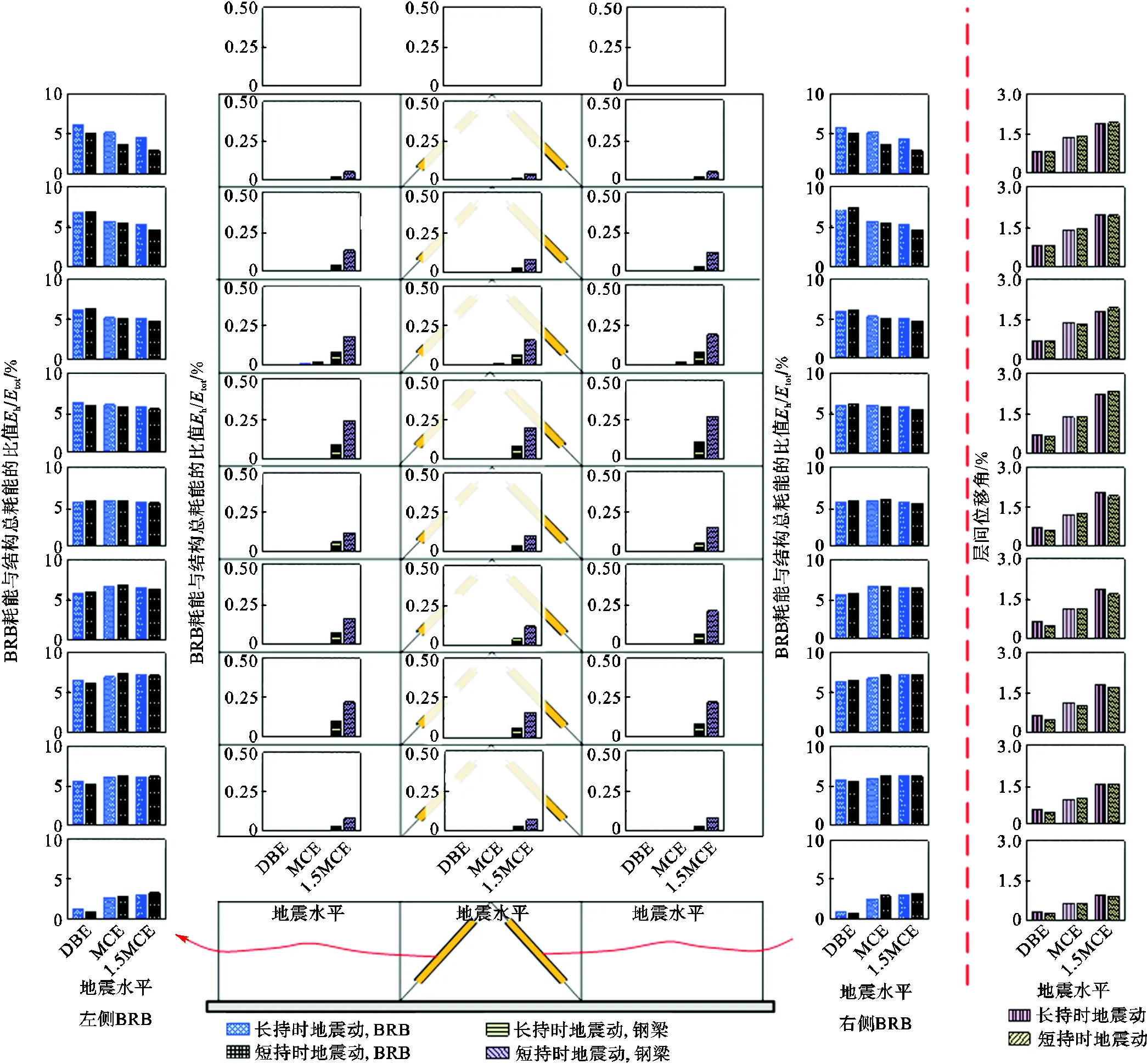
图7 屈曲约束支撑和钢梁在设防地震、罕遇地震和1.5倍罕遇地震下的耗能比以及层间位移响应

4 地震易损性分析

4.1 工程需求参数的选取

在建筑结构的地震易损性分析中，工程需求参数和地震动强度参数一般采用层间位移角(m)和结构基本周期5%阻尼比对应的谱加速度(Sa(1，5%))，并得到了较为广泛的认可和应用．因此，本节首先采用表3中的长、短持时地震动对9层典型3跨子结构进行增量动力分析(incremental dynamic analysis，IDA)，以Sa(1，5%)＝0.025，0.1，0.2，…为幅值对地震动进行调幅，IDA曲线见图8．

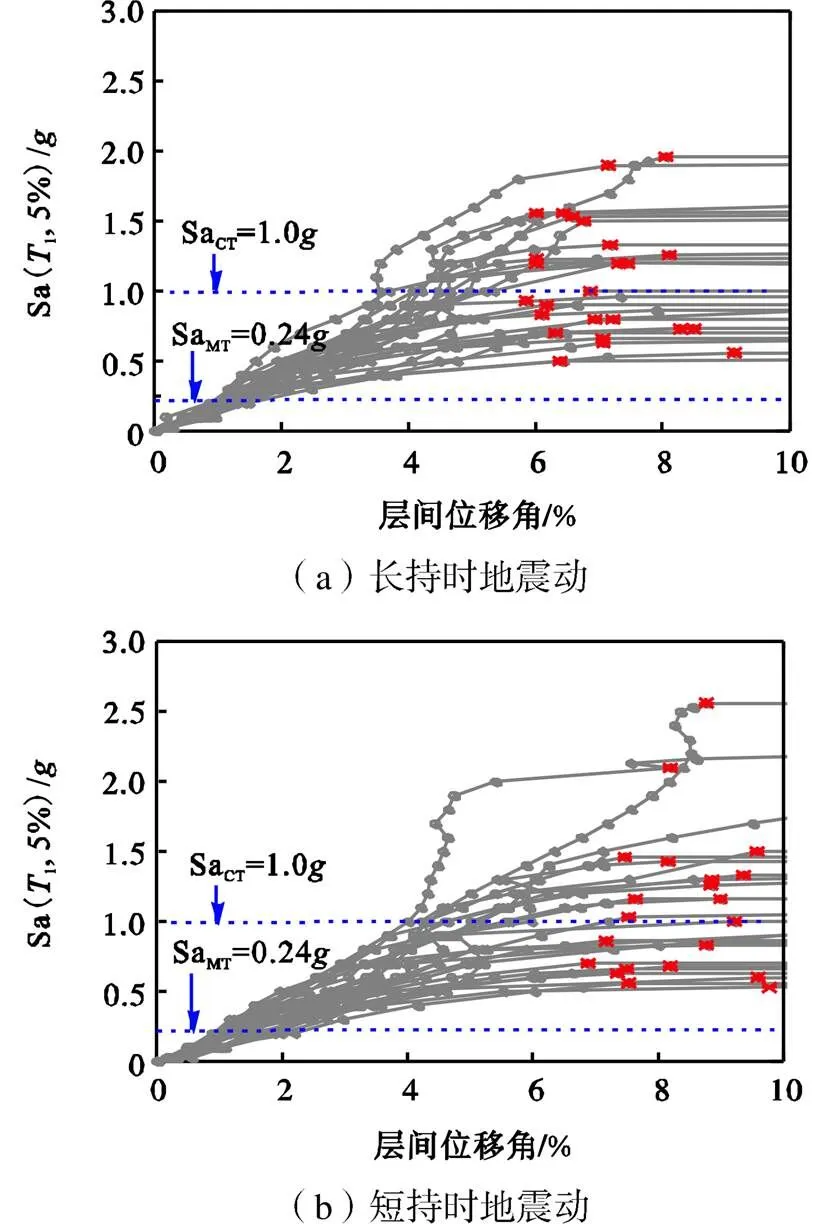
图8 IDA曲线(qm，Sa(T1，5%))

FEMA P695[23]建议的倒塌点：一组地震动作用下，结构的IDA曲线的切线斜率降为初始斜率中位值的20%时对应的点与m=10%时对应的点，取两者中数值较小的点作为结构的抗地震倒塌点．建议的倒塌储备系数CMR用于表征结构的实际抗倒塌能力与设计要求须达到的抗倒塌能力之间的储备关系，即

CMR＝SaCT/SaMT(3)

式中：SaCT表示一组地震动作用下，恰有50%的地震动使结构发生倒塌时对应的谱加速度；SaMT表示50年超越概率为2%的罕遇地震在基本周期1处对应的谱加速度．

由式(3)可得，结构在长、短持时地震动作用下的CMR均为4.2，远大于1.0，具有较好的抗倒塌能力.但其CMR值相等，说明以m作为工程需求参数不能准确反映地震动持时对结构累积损伤的影响，也不能较好地反映结构在长、短持时地震动下的真实抗倒塌能力．

进一步地，本文采用Park-Ang提出的损伤指标作为工程需要参数来反映地震动持时对结构累积损伤的影响[24]，即

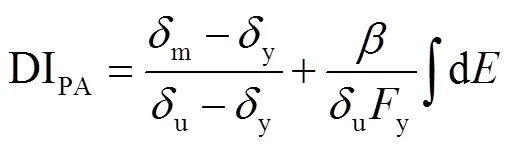
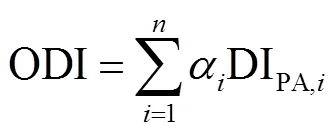
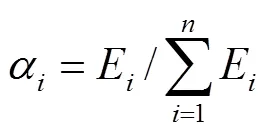
式中：y、u和m分别表示构件的屈服变形、极限变形和地震下历经的最大变形；为耗能因子；y为构件的屈服强度；E表示第个构件的累积滞回耗能；DIPA和ODI分别表示构件损伤因子和结构整体损伤因子．

定义ODI为1.0时，结构发生倒塌[14]．根据式(4)～(6)和图8的倒塌点，得9层子结构在长短持时地震动下的耗能因子的中位值为0.098．据此，可得结构以(ODI，Sa(1，5%))为形式的IDA曲线，见图9．

由图9可知，9层结构在长、短持时地震动下的倒塌储备系数CMR分别为2.9和3.8，均大于1.0．短持时地震下的CMR比长持时的大31.0%；长持时地震动下的倒塌中位值比短持时的小24.0%，主要是由于ODI既考虑了结构的变形，又考虑了累积耗能．这表明相比于层间位移角m，以整体损伤因子ODI作为工程需求参数可以较为准确地反映长、短持时地震动对结构累积损伤的影响．

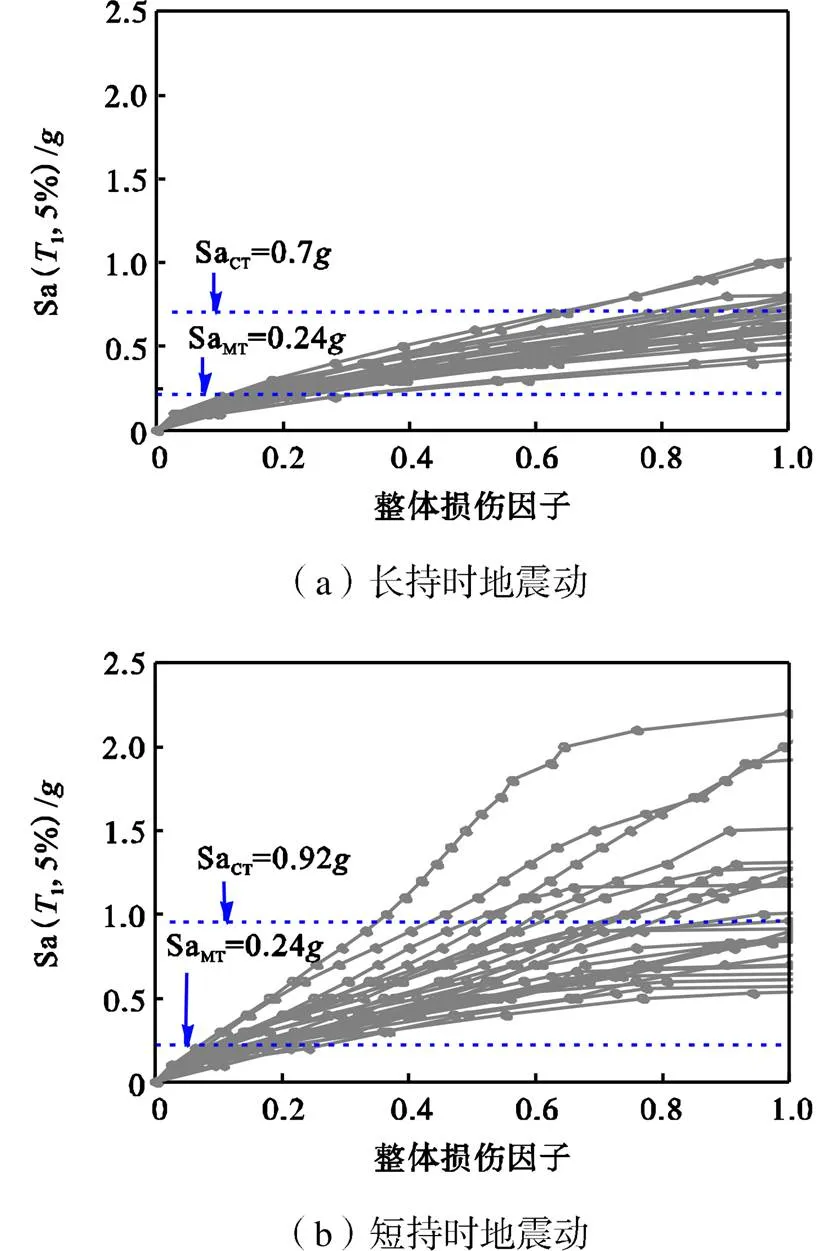
图9 IDA曲线(ODI，Sa(T1，5%))

4.2 地震动强度参数的选取

工程需求参数D|IM和地震动强度参数IM之间一般服从幂指数回归关系，即

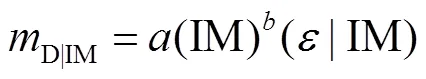
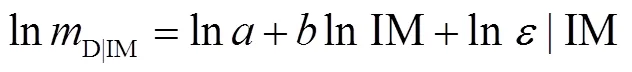
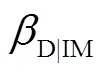
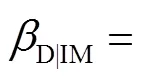
合适的地震动强度指标应具有实用性、有效性、充分性和调幅鲁棒性．实用性是指强度指标与工程需求参数之间具有直接的相关性，采用参数评价；有效性一般采用对数标准差D|IM和皮尔逊评价；充分性是指结构在给定地震动强度下，工程需求参数与地震动参数(如震级w和震中距等)条件独立，采用式(8)中的ln|IM对w或ln的线性回归曲线的值进行衡量．调幅鲁棒性是指结构在调幅前后的地震动作用下的地震响应与调幅系数无趋势关系，采用ln|IM对lnSF的线性回归曲线的值进行衡量，SF为地震动的调幅系数．

经过初步筛选，选取考虑了地震动谱加速度和重要持时的综合指标NP-D作为地震动强度参数[21]．

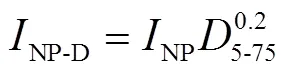
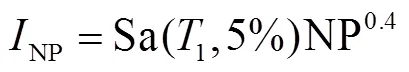
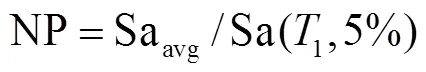
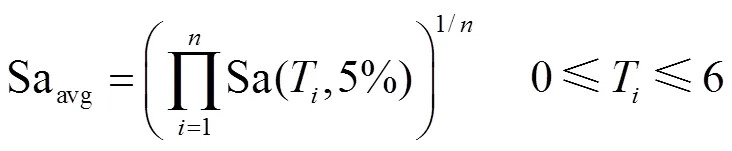
式中Sa(T)表示周期T对应的谱加速度．

以9层子结构在长持时地震动作用下的响应为例，图10展示了地震动强度参数NP-D与工程需求参数ODI之间的对数线性关系以及值检验．表4给出了Sa(1，5%)和NP-D的评价结果．

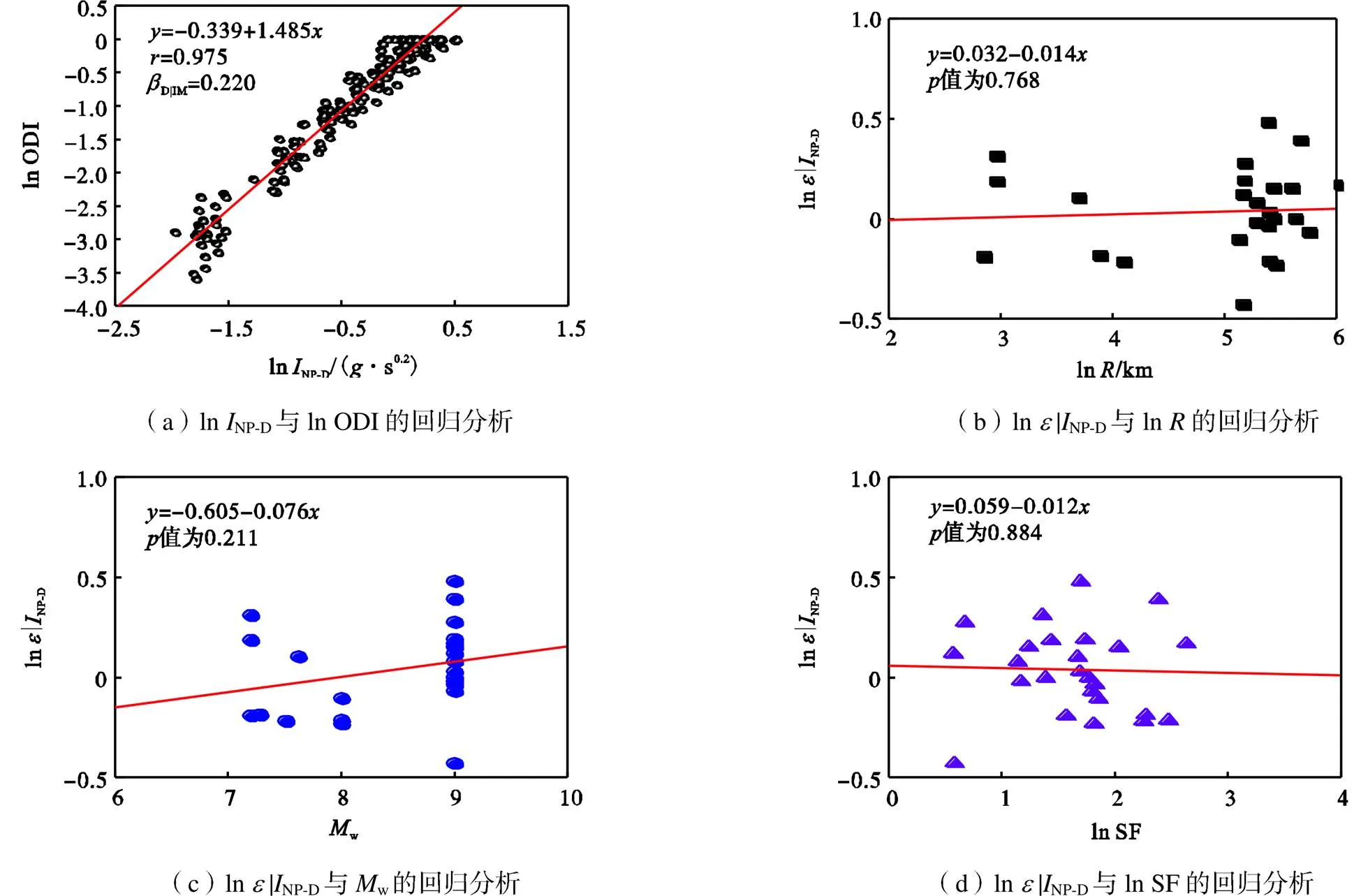
图10 INP-D和ODI的回归分析(长持时地震动)

表4 地震动强度指标的评价

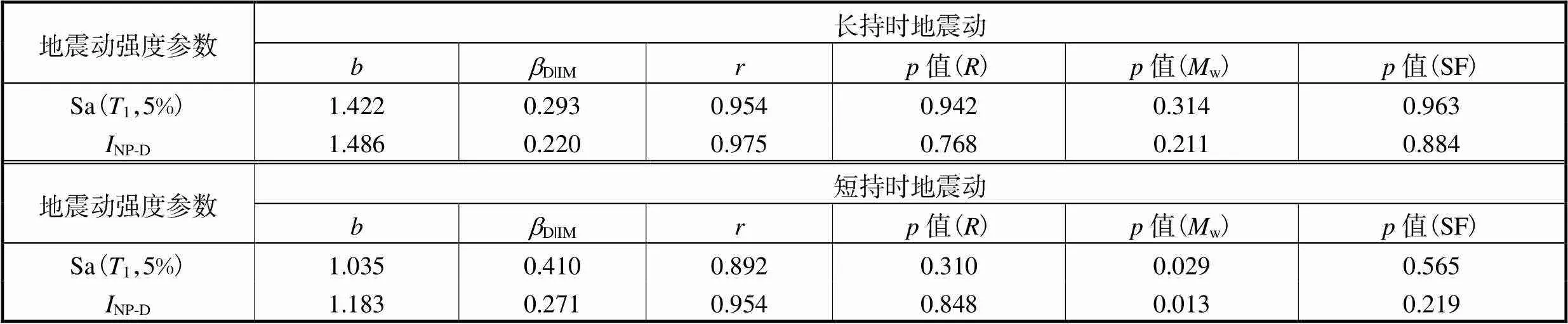
Tab.4 Assessment of the ground motion intensity measure

由表4可知，9层子结构在长、短持时地震动作用下，NP-D的值和皮尔逊值均大于Sa(1，5%)对应的数值，且NP-D的对数标准差D|IM小于Sa(1，5%)的数值．这表明相比于Sa(1，5%)，NP-D与ODI之间的对数线性更加显著，数据的离散性更小．另一方面，NP-D的ln|IM对w、ln和lnSF的值虽然整体小于Sa(1，5%)的数值，但均远大于0.05，表明Sa(1，5%)和NP-D均具有较好的充分性和调幅鲁棒性．以ODI为工程需求参数时，NP-D的综合性能优于Sa(1，5%)．

4.3 易损性曲线

结构的易损性函数一般可表示为

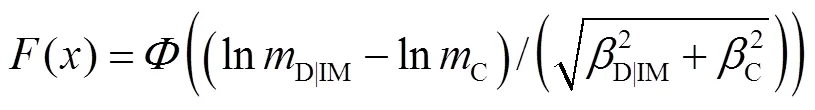
式中：(×)为标准正态概率分布函数；D|IM和D|IM分别为仅考虑偶然不确定性的结构地震需求的中位值和对数标准差；C和C分别为仅考虑偶然不确定性的结构抗震能力的中位值和对数标准差．

参考ATC-13[25]，结构抗震能力分为轻微破坏、中等破坏、严重破坏和倒塌4个损伤状态，对应的ODI范围分别为0～0.2、0.2～0.4、0.4～1.0和＞1.0.C取0.25以考虑认知的不确定性[23]．基于式(13)，可得9层钢管混凝土框架-屈曲约束支撑结构在不 同地震水平下超越不同损伤状态的易损性曲线，见图11．

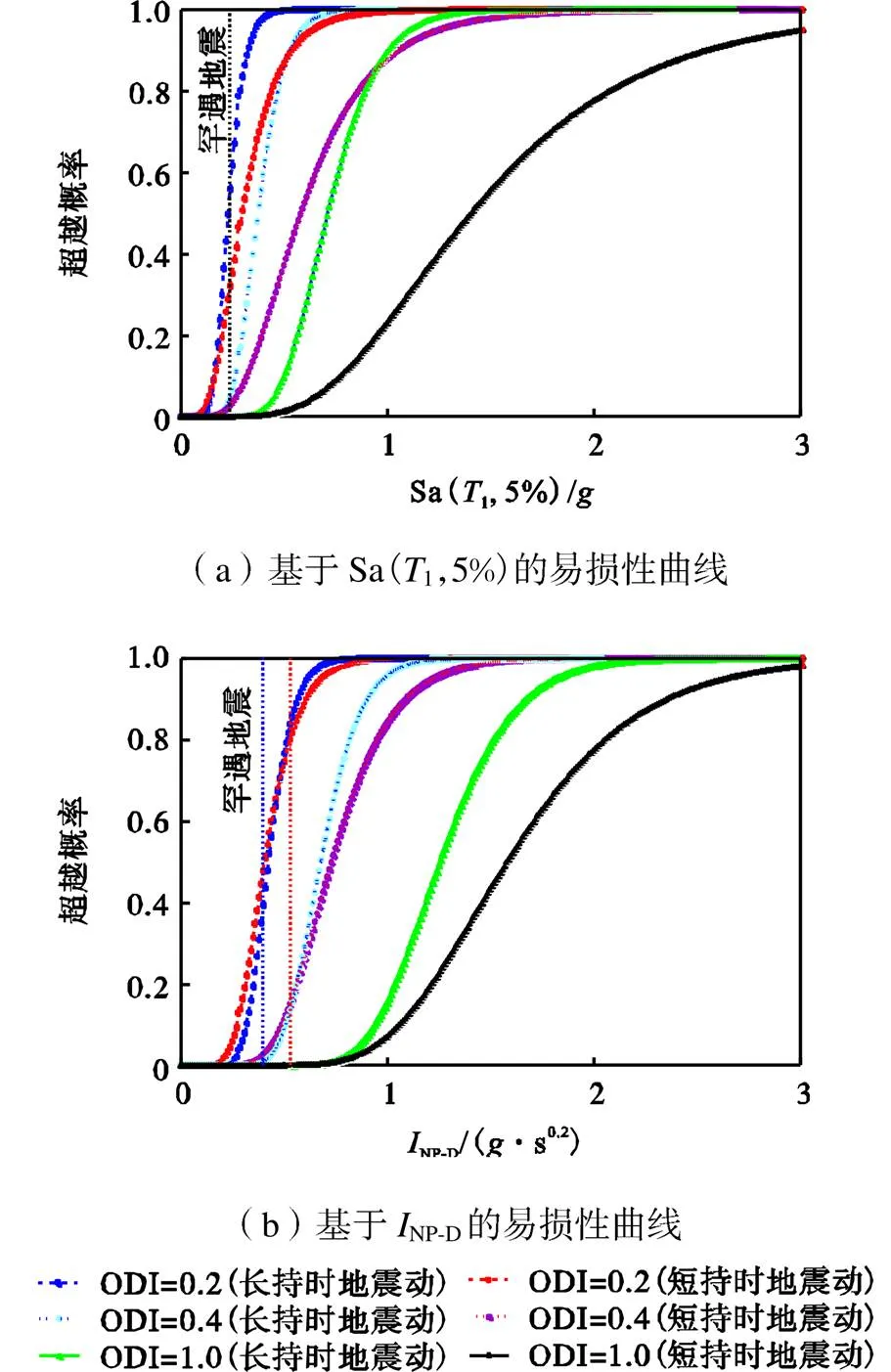
图11 结构的易损性曲线

以罕遇地震水平为例，结合图11可知，采用Sa(1，5%)和NP-D为地震动强度指标时，结构发生倒塌的概率均为0，分析结果一致．对于Sa(1，5%)，长持时地震动下的ODI超越0.2和0.4的概率分别为0.56和0.05，短持时地震动下的超越概率分别为0.317和0.028；对于NP-D，长持时地震动下的ODI超越0.2和0.4的概率分别为0.836和0.135，短持时地震动下的超越概率分别为0.479和0.027．NP-D的超越概率整体上大于对应的Sa(1，5%)的概率值，表明NP-D对地震动持时产生的结构损伤更加敏感．对于Sa(1，5%)，长持时地震动下的ODI超越0.2和0.4的概率分别是短持时的1.77倍和1.79倍；对于NP-D，长持时地震动下的ODI超越0.2和0.4的概率分别是短持时的1.74倍和5.0倍．这表明相比于短持时地震动，长持时地震动较为明显地增大了结构的损伤，结构的抗震分析应关注地震动持时对结构的影响．

5 结 论

通过对钢管混凝土框架-屈曲约束支撑结构的抗震性能试验和地震动持时影响下的易损性分析，可以获得下列结论．

(1) 试验结果表明：钢管混凝土框架-屈曲约束支撑试件的水平荷载-水平位移滞回曲线饱满且稳定，试件破坏前基本未出现承载力下降．

(2) 通过试验结果验证了OpenSees弹塑性分析模型的准确性；9层结构的非线性时程分析表明层间位移角基本满足在多遇、设防和罕遇地震下预期设定的目标限值，变形沿楼层高度分布较为均匀．

(3) 相比于层间位移角，以整体损伤因子作为工程需求参数可以较为准确地反映地震动持时对结构累积损伤的影响；相比于短持时地震动，长持时地震动下结构的倒塌中位值比短持时地震动小24%．

(4) 以整体损伤因子为工程需求参数时，相比于Sa(1，5%)，考虑地震动谱加速度和重要持时的地震动强度指标NP-D表现出更优的实用性、有效性、充分性和调幅鲁棒性．

(5) 相比于短持时地震动，长持时地震动比较明显地提高了结构的累积损伤和不同损伤状态的超越概率；钢管混凝土框架-屈曲约束支撑结构的抗震设计和分析应关注地震动持时对结构的影响．

［1］ 韩林海，牟廷敏，王法承，等. 钢管混凝土混合结构设计原理及其在桥梁工程中的应用[J]. 土木工程学报，2020，53(5)：1-24.

Han Linhhai，Mu Tingmin，Wang Facheng，et al. Design theory of CFST(concrete-filled steel tubular)mixed structures and its applications in bridge engineering[J]. China Civil Engineering Journal，2020，53(5)：1-24(in Chinese).

［2］ Tsai K C，Hsiao P C. Pseudo-dynamic test of a full-scale CFT/BRB frame—PartⅡ：Seismic performance of buckling-restrained braces and connections[J]. Earthquake Engineering & Structural Dynamics，2008，37(7)：1099-1115.

［3］ 贾明明，孙 霖，郭兰慧，等. 防屈曲支撑非屈服段平面外屈曲对组合框架支撑结构性能的影响[J]. 建筑结构学报，2013，34(增1)：383-388.

Jia Mingming，Sun Lin，Guo Lanhui，et al. Influences of out-of-plane buckling of non-yielding segments of BRBs on braced composite frame structure[J]. Journal of Building Structures，2013，34(Suppl 1)：383-388(in Chinese).

［4］ 于敬海，郑达辉，胡相宜，等. 方钢管混凝土组合异形柱防屈曲支撑框架抗震性能试验[J]. 天津大学学报(自然科学与工程技术版)，2018，51(增1)：135-142.

Yu Jinghai，Zheng Dahui，Hu Xiangyi，et al. Experiment on seismic performance of buckling-restrained braced frame composed of special-shaped concrete-filled square steel tube columns[J]. Journal of Tianjin University(Science and Technology)，2018，51(Suppl 1)：135-142(in Chinese).

［5］ 王 波，王静峰，孙 政，等. 屈曲约束支撑装配式钢管混凝土组合框架抗震试验性能研究[J]. 土木工程学报，2018，51(6)：14-22.

Wang Bo，Wang Jingfeng，Sun Zheng，et al. Experimental study on seismic behavior of assembly CFST composite frames with bucking restrained braces[J]. China Civil Engineering Journal，2018，51(6)：14-22(in Chinese).

［6］ Li B B，Wang J F，Yang J，et al. Pseudo-dynamic response and analytical evaluation of blind bolted CFT frames with BRBs [J]. Journal of Constructional Steel Research，2020，166：195744.

［7］ 江 浩，徐龙河. 自复位耗能支撑滞回特性及钢框架抗震性能分析[J]. 天津大学学报(自然科学与工程技术版)，2021，54(3)：237-244.

Jiang Hao，Xu Longhe. Study on hysteretic performance of self-centering energy dissipation braces and seismic behaviors of braced frames[J]. Journal of Tianjin University(Science and Technology)，2021，54(3)：237-244(in Chinese).

［8］ 李国强，孙飞飞，邓仲良，等. 屈曲约束支撑抗震性能试验研究[J]. 建筑结构，2014，44(18)：71-78.

Li Guoqiang，Sun Feifei，Deng Zhongliang，et al. Experimental study on the aseismic performance of buckling-restrained braces[J]. Building Structure，2014，44(18)：71-78(in Chinese).

［9］ 陈志华，黄培华，余玉洁. 局部低强防屈曲支撑耗能性能试验研究[J]. 天津大学学报(自然科学与工程技术版)，2017，50(增1)：59-67.

Chen Zhihua，Huang Peihua，Yu Yujie. Energy dissipation performance of local steel strength weakened buckling-restrained brace[J]. Journal of Tianjin University(Science and Technology)，2017，50(Suppl 1)：59-67(in Chinese).

［10］ 周 云，龚 晨，钟根全，等. 开孔钢板装配式屈曲约束支撑设计方法研究[J]. 土木工程学报，2019，52(12)：57-65.

Zhou Yun，Gong Chen，Zhong Genquan，et al. Study on design method of perforated steel-plate assembled buckling-restrained brace[J]. China Civil Engineering Journal，2019，52(12)：57-65(in Chinese).

［11］ GB 50011—2010建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2010.

GB 50011—2010Code for Seismic Design of Buildings [S]. Beijing：China Architecture & Building Press，2010(in Chinese).

［12］ Chandramohan R，Baker J W，Deierlein G G. Quantifying the influence of ground motion duration on structural collapse capacity using spectrally equivalent records[J]. Earthquake Spectra，2016，32(2)：927-950.

［13］ Belejo A，Barbosa A R，Bento R. Influence of ground motion duration on damage index-based fragility assessment of a plan-asymmetric non-ductile reinforced concrete building[J]. Engineering Structures，2017，151：682-703.

［14］ Pan Y X，Ventura C E，Tannert T. Damage index fragility assessment of low-rise light-frame wood buildings under long duration subduction earthquakes[J]. Structural Safety，2020，84：101940.

［15］ 韩建平，程诗焱，于晓辉，等. 地震动持时对RC框架结构易损性与抗震性能影响[J]. 建筑结构学报，2021，42(11)：116-127.

Han Jianping，Cheng Shiyan，Yu Xiaohui，et al. Effect of ground motion duration on seismic fragility of RC frame structures[J]. Journal of Building Structures，2021，42(11)：116-127(in Chinese).

［16］ Li B B，Wang J F，Wang Y Q，et al. New performance-based plastic design and evaluation of blind bolted end-plate CFT composite frames with BRBs[J]. Engineering Structures，2021，232(82)：111806.

［17］ Mckenna F. OpenSees：A framework for earthquake engineering[J]. Computing in Science & Engineering，2011，13(4)：58-66.

［18］ DB 34/T 5069—2017 屈曲约束支撑结构技术规程[S]. 合肥：安徽省工程建设标准设计办公室，2017.

DB 34/T 5069—2017 Technical Specification for Buckling-Restrained Brace Structures[S]. Hefei：Anhui Engineering Construction Standard Design Press，2017(in Chinese).

［19］ Lignos D G，Krawinkler H. Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading[J]. Journal of Structural Engineering，2011，137(11)：1291-1302.

［20］ Zsarnóczay Á，Vigh L G. Eurocode conforming design of BRBF—Part Ⅱ：Design procedure evaluation[J]. Journal of Constructional Steel Research，2017，135：253-264.

［21］ Jamshidiha H R，Yakhchalian M，Mohebi B. Advanced scalar intensity measures for collapse capacity prediction of steel moment resisting frames with fluid viscous dampers[J]. Soil Dynamics and Earthquake Engineer-ing，2018，109：102-118.

［22］ Li B B，Wang J F，Yang J，et al. Probabilistic seismic performance evaluation of composite frames with concrete-filled steel tube columns and buckling-restrained braces[J]. Archives of Civil and Mechanical Engineer-ing，2021，21(2)：1-22.

［23］ FEMA P695. Quantification of Building Seismic Performance Factors[R]. Washington，DC：Federal Emergency Management Agency，2009.

［24］ Park Y J，Ang A H S. Mechanistic seismic damage model for reinforced concrete[J]. Journal of Structural Engineering，1985，111：722-739.

［25］ ATC-13. Earthquake Damage Evaluation Data for California[R]. Washington，DC：Applied Technology Council，1985.

Probabilistic Seismic Fragility Evaluation of CFST Frames with Buckling-Restrained Braces

Wang Jingfeng1, 2，Li Beibei1, 3，Wang Yuanqing3，Li Guoqiang1, 2

(1. College of Civil Engineering，Hefei University of Technology，Hefei 230009，China；2. Key Laboratory of Anhui Civil Engineering Structures and Materials，Hefei University of Technology，Hefei 230009，China；3. Key Laboratory of Civil Engineering Safety and Durability of China Ministry of Education，Tsinghua University，Beijing 100084，China)

A nine-story structure was designed based on a plastic design method using energy balance to investigate the seismic behavior and the influence of ground motion duration on the probabilistic seismic fragility for the concrete-filled steel tube(CFST)frames with buckling-restrained braces(BRBs). Low cyclic testing and numerical analysis were performed on a one-bay one-story braced frame specimen. The elastic-plastic analytical model of the nine-story typical three-span substructure was established using the OpenSees program. The effect of ground motion duration on the seismic intensity performance of the structure was analyzed via fragility curves using various engineering demand parameters(EDPs)and intensity measuresobtained from incremental dynamic analysis. The analysis results showed that the hysteretic curve of the test specimen is plump and stable. BRBs dissipated 90% of the hysteretic energy of the structure. Meanwhile，the overall damage index(ODI)could better reflect the influence of the ground motion duration on the cumulative damage effect of the structure. Long-duration ground motions reduced the median value of structural collapse by 24% compared to short-duration ground motions. With ODI as the EDP，the combined indexNP-D，which considers spectrum acceleration and a significant duration，shows excellent practicability，efficiency，sufficiency，and scaling robustness. For theNP-D，the probabilities of ODIexceeding 0.2 and 0.4 under long-duration ground motion were 1.74 and 5.0 times that under a short-duration ground motion，respectively，for the structure subjected to rare earthquakes. Therefore，the influence of ground motion duration on the cumulative damage for CFST frames with BRBs should be considered during structural seismic design and analysis.

ground motion duration；concrete-filled steel tube(CFST) frame；buckling-restrained brace(BRB)；fragility curve；damage index

10.11784/tdxbz202109026

TU391

A

0493-2137(2023)03-0311-12

2021-09-17；

2021-10-18.

王静峰（1976—  ），男，博士，教授，jfwang008@163.com.

李贝贝，lbbhfut@163.com.

国家自然科学基金资助项目(51478158)；中央高校基本科研业务费专项资金资助项目(JZ2021HGQA0249，JZ2021HGTA0156)；中国博士后科学基金资助项目(BX20200193).

Supported by the National Natural Science Foundation of China(No. 51478158)，the Fundamental Research Funds for the Central Universities(No. JZ2021HGQA0249，No. JZ2021HGTA0156)，the China Postdoctoral Science Foundation(No. BX20200193).

(责任编辑：樊素英)