基于第一性原理的单层WS2热输运特性研究

2023-03-14刘远超张厚梁钟建斌蒋旭浩徐一帆

人工晶体学报 2023年2期

关斌,刘远超,张厚梁,钟建斌,邵钶,蒋旭浩,徐一帆

(北京石油化工学院机械工程学院，北京 102617)

0 引言

随着纳米技术的发展，半导体微处理器的频率和集成度越来越高，致使芯片上单位面积的功率密度急剧增加，由此带来的芯片散热问题已成为目前制约器件发展的一个关键因素。因此，寻找电子和散热性能更优异的新材料，对其进行热输运特性研究，对于设计和制造微/纳电子器件具有重要的意义。

WS2是一种二维层状过渡金属硫化物，具有比石墨烯更优异的物理性能，例如可调带隙[1]、高开关电流比[2]、高电子迁移率[3]，以及较高的塞贝克系数[4]等，实验表明WS2具有良好的导热性能[5]，在电子器件散热领域[6-8]及纳米复合材料领域[9-10]具有良好的应用前景。因此，深入研究WS2的热输运特性将有助于未来高集成度及高频率电子器件[11]的发展。

目前，通过实验可以测量WS2的热导率，但实验所需成本较高，且实验结果因受许多因素影响而存在一定的不确定性。另外，目前WS2高热导率的微观机理仍不清楚，尤其是WS2的热输运特性无法从实验获得，而对其微观模拟是研究热输运机理的一种有效方法。本文拟从量子力学出发，应用密度泛函理论(density functional theory, DFT)结合玻尔兹曼输运方程(Boltzmann transport equation， BTE)，利用第一性原理方法计算单层WS2的热导率，并从谐性效应和非谐性效应两方面深层次分析单层WS2的热输运微观机理，为调控和改进WS2的热输运性能提供借鉴和参考。

1 模型和方法

1.1 计算模型

1T相单层WS2的晶体结构类似于“三明治”构型，如图1所示。整体呈蜂窝状，两层硫原子中间夹着一层钨原子，S—W—S分子团以共价键链接成六方形网络。

图1 单层WS2的晶体结构

1.2 结构优化

本文对参数进行收敛性测试，主要包括优化截断能(ENCUT)和K点网格密度两个参数，目的是确保计算符合精度要求(其中每个原子的能量收敛精度为1×10-8eV，每个原子上的力小于1×10-5eV/Å)。测试结果最终取截断能为640 eV，k点网格密度取11×11×1。

对单层WS2进行结构优化时，只优化a和b方向的晶格常数，为了消除相邻分子层的影响，在z方向构建了2 nm的真空层。优化前的晶格常数a=b=0.319 0 nm，相邻W—S原子的距离为0.242 24 nm，S—W—S原子夹角为82.382°；优化后的晶格常数a=b=0.318 8 nm，相邻W—S原子的距离为0.242 03 nm，S—W—S夹角为82.394°。

1.3 模拟方法

本文利用VASP[12]软件，采用基于第一性原理[13]的密度泛函理论，选取PAW[14]的PBE交换关联势[15]计算晶格热导率。其中，计算声子谱选用超胞法(5×5×1)，计算二阶力常数采用密度泛函微扰理论(density functional perturbation theory, DFPT)[16]，计算三阶力常数选用3×3×1超胞并考虑第三近邻原子。最后，利用ShengBTE软件求解BTE方程[17]，得到单层WS2的晶格热导率。

本文计算得到二维纳米单层WS2的晶格热导率后，通过计算其声子色射曲线、声子群速度、声子寿命、格林艾森参数和三声子散射过程的加权相空间，以及累积晶格热导率随平均自由程和频率的变化规律等，深入阐述WS2中声子行为的热输运机理。本文的具体计算流程示意图如图2所示。

图2 计算流程示意图

2 计算结果与讨论

2.1 晶格热导率及热力学性质

由于存在真空层，在计算时材料体积被扩大，故得到的二维材料热导率数值会偏小，因此需要根据材料的实际厚度进行修正。修正系数为c/h，c是垂直材料方向(一般为z方向)的晶格常数，h是二维材料的有效厚度。

本文所用的声子玻尔兹曼输运方程为：

(1)

式中：q和s分别代表波矢的声子支和分支指数；vα和vβ分别是沿α方向和β方向的声子群速度；τqs为声子弛豫时间；Cv表示声子支热容量。

本文采用BTE迭代法和弛豫时间近似法(RTA)，分别计算了同位素纯(无掺杂)和天然(有掺杂)单层WS2的晶格热导率，发现在zigzag方向和armchair方向的值相同，说明单层WS2结构具有高度对称性，这与一些单层TMDC材料(如MoS2、MoSe2)相似[18-19]。通过第一性原理计算，本文得到300 K时天然(有掺杂)单层WS2的热导率为149.12 W/(m·K)。

目前，利用拉曼光谱、时域热反射(TDTR)和稳态实验方法均可以测量出单层WS2的热导率，表1列举了目前单层WS2热导率的主要实验研究结果(300 K)。从表1可以看出，本文计算结果与Pisoni等采用稳态法测量的热导率(124 W/(m·K))最为接近。

表1 单层WS2热导率的主要实验研究结果(300 K)

从表1可以看出，单层WS2热导率的实验测量值之间存在着一定差异。本文认为实验结果存在差异的原因可能是：1)声子的边界散射(实验样品的长度有限)；2)实验样品边缘粗糙程度不同；3)实验样品存在某些缺陷；4)实验选取的材料衬底不同(衬底效应会降低测量结果)。其中，Gertych等较低的测量结果主要归因于重叠薄片之间的附着和相互作用增加了声子边界散射，这极大地限制了面内热传导。

图3给出了单层WS2(zig方向)的热导率和热力学性质随温度的变化关系曲线。

图3 单层WS2的热导率和热学性质随温度的变化关系

从图3(a)可以看出，在0～1 000 K，单层WS2的热导率随温度的升高而降低。这是由于温度升高导致Umklapp声子散射(倒逆过程)增加，最终导致热导率单调下降。其中，曲线③(无掺杂)和④(同位素掺杂)是采用RTA法计算的结果，其结果都比迭代法计算的值要低很多(无掺杂时采用迭代法算得的数值为175.08 W/(m·K)；RTA法算得的数值为100.47 W/(m·K))。这是因为RTA方法将正常的三声子过程视为热阻[26]，而且忽略了声子具体的真实分布，计算结果存在一定误差，因此本文重点分析迭代法计算的结果。

图3(a)中的曲线①和②为BTE迭代法的计算结果，考虑同位素掺杂时WS2的热导率比纯WS2的热导率小，说明同位素掺杂后增强了WS2体系的声子散射，导致热导率偏小。随着温度的继续升高，二者数值逐渐降低并且趋于一致。这是由于在高温下，同位素无序对热导率的影响减弱，且高频声子被激活，增强了声子Umklapp散射的效果，进一步阻碍声子的热传输。

综合图3(b)来看，声子无序性散射增强，表现为体系的熵增加。200～500 K时，WS2的热导率下降速度很快，而在超过500 K后，其热导率的变化趋势逐渐变缓。这是因为单层WS2在极低温度(0～100 K)下的定容比热容与温度之间呈现T3的关系(见图3(b)Cv曲线)，结合公式(1)可知低温时WS2的热导率较高，高温(超过600 K)时其比热容达到饱和值(73.5 J/(K·mol))，此即Dulong-Petit law(杜隆-佩蒂特定律)经典极限，这与图3(a)中热导率随温度曲线的变化趋势相对应。

图4给出了不同温度下各个声子支对单层WS2总热导率的贡献情况。结果表明声学声子支起主要作用，特别是纵向声学(longitudinal acoustic, LA)声子支，具有最大的热导率贡献百分比。在300 K时，ZA、TA、LA、ZO、TO、LO声子支对总热导率的贡献百分比分别为29.51%、25.82%、44.28%、0.23%、0.34%、0.04%。在极低温下，面外声学(z-direction acoustic, ZA)声子支展现出独特的性质，说明ZA声子支在低温时对热导率的影响较为特殊。同时也可以看出，光学声子支(ZO、TO、LO)对热导率的贡献占比非常小，故在后文分析中忽略光学声子支对WS2热导率的影响。

图4 各声子支对WS2总热导率的贡献百分比

为了更深入地了解非谐波特性对单层WS2热输运的影响程度及规律，本文将从谐性效应(声子色射关系曲线和声子群速度)和非谐性效应(声子弛豫时间、格林艾森参数及三声子散射等)两方面深入探讨单层WS2的热输运机理。

2.2 声子输运的谐性效应

2.2.1 声子色散关系

声子色散关系曲线(phonon dispersion curves, PDC)展示了声子支振动的分布情况。本文通过计算得到WS2的声子谱及声子态密度图，如图5所示。

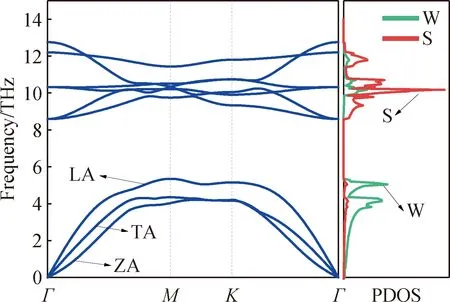
图5 单层WS2的声子谱和声子态密度

图5给出的声子谱中呈现了9条声子支曲线，对应WS2原胞内的3个原子，9条声子支曲线包括3条声学声子支曲线和6条光学声子支曲线。图5中位于下部的3条声子支曲线表示3个声学声子支曲线，位置由低到高依次是单层WS2的ZA声子支曲线、面内横向声学(transverse acoustic, TA)声子支曲线和面内LA声子支曲线。

从图5可以看出，布里渊区里的所有声子支均为正值，表明计算的WS2结构具有很好的力学稳定性和动力学稳定性。图5中的3个声学声子支曲线相交且接近于0(Г点)，说明声学声子支存在简并态。在Г点附近，ZA曲线呈抛物线状，TA曲线和LA曲线则呈现线性特征，这是二维材料的结构特征[27]。Г点附近出现抛物线状的ZA曲线是由于单层结构中声子沿面外和面内振动的去耦合。另外还可以看出，单层WS2的声学声子支和光学声子支之间有较大的带隙，说明声学支和光学支之间没有强散射作用，这也是导致单层WS2具有相对较高晶格热导率的原因之一。

声子态密度(PDOS)从宏观上可理解为体系内声子的分布概率，从微观上可认为是声子处于某种状态的概率。在图5的WS2的声子PDOS图中，可以看到低频区内W原子的声子态密度远大于S原子声子态密度，故W原子对于声子谱的贡献远大于S原子；而在高频区则恰好相反。这可能是由于受两类原子(W原子和S原子)的原子质量和原子间键长不同的影响，原子质量和原子间键长的增加导致了原子间共价键键能的减小。

2.2.2 声子群速度

图6给出了300 K时，单层WS2的声子群速度随频率和波矢的变化关系。从图6(a)可以看出，单层WS2的声学和光学声子支分别分布在低频区和高频区，且低频声学支的群速度大于光学支群速度，这说明单层WS2的声学声子支对热传输影响较大。单层WS2声学声子群速度的大体变化规律是随着频率的增加而逐渐减小，其中LA的声子群速度比ZA和TA的声子群速度大，因此可以认为LA模式对WS2的热导率的贡献最大。

图6 单层WS2在300 K时的声子群速度随频率(a)和波矢(b)的变化关系

从图6(b)可以看出，所有声子支在高对称线M-K上都出现了峰值，且在布里渊区边界处的速度均为零。峰值出现的原因可能是WS2的结构在层间(z方向)方向上的对称性遭到破坏。声子支在布里渊区边界处的速度为零，说明布里渊区边界声子振动模式发生软化，晶格存在严重的边界色散。ZA声子支在Γ-M、K-Γ上也出现了峰值，说明ZA对晶格波动较为敏感，对热输运的影响较大。另外，基于公式(1)可知，声子群速度对WS2热导率的影响比热容量和声子寿命的影响更大。

2.3 声子输运的非谐性效应

2.3.1 声子弛豫时间

为了更深入研究非谐波特性对WS2热输运特性的贡献，本文计算了WS2的声子寿命，如图7所示。

从图7可以看到，随着频率的增大，声学声子寿命大幅度降低，这与群速度变化相对应。另外，相比ZA和TA，LA模式具有较高的声子寿命，这可能是由于LA声子支具有较大的群速度和较少的散射通道，而较少的散射通道可以抑制散射率，因此声子寿命也随之降低。

图7 单层WS2在300 K时的声子弛豫时间随频率的变化

2.3.2 格林艾森参数

格林艾森参数(Grüneisen parameter)γ主要用来描述声子的非简谐作用，它可以定量地描述晶体声子的非谐振性，衡量三声子的散射强弱。图8给出了单层WS2的格林艾森参数γ随频率变化的规律。

图8 单层WS2在300 K时的格林艾森参数随频率的变化

如图8所示，在低频区观察到ZA声子支的γ有大部分负值和少数正值，这与二维材料石墨烯、MoS2和MoSe2等类似[28]。这主要是因为ZA声子支在弛豫的过程中，产生的拉伸应变改变了其固有的振动频率；同时也与二维材料低晶格维度的薄膜效应有关[29-30]。随着频率的增加(低频区内)，ZA声子支的值也逐渐增大，说明ZA声子支的相互作用在增强。

为了便于观察，取图8中部分区间作放大处理，可以看到在4 THz左右时，TA和LA声子支出现了负值。这是由WS2自身的化学键所致，当弛豫过程中应变导致的化学键弯曲或者拉伸时，γ值也随之发生变化；同时，此时的ZA越来越强，三种声子支相互作用达到最强，声子色散增强，最终也会导致部分γ变为负值。说明不同频率的声子其振动会有很大的变化。理论上讲，如果可以调控声子的频率，那么就可以改变晶格的振动情况，从而达到调控晶格热导率的效果。本文计算了不同温度下(300、450、600 K)单层WS2各声子支的平均格林艾森参数γ，其值分别约为0.032、0.041、0.045，发现温度对单层WS2的格林艾森参数的影响并不明显。

综上分析，在低频区内对γ主要产生贡献的是TA和LA声子支，其中LA的贡献最大，这说明在单层WS2内，沿着面内纵向的声子运动最剧烈。

2.3.3 三声子散射相空间

除了散射强度外，声子的散射通道数对晶格热导率也有很大影响。相空间P3代表了三声子过程的声子散射通道的数量[31]。图9给出了单层WS2的三声子散射相空间，其中图9(a)表示吸收过程，图9(b)表示湮灭过程，图9(c)表示三声子过程。

图9 单层WS2在300 K时三声子的散射相空间的频率依赖性

从整体来看，低频区声子的吸收过程和三声子过程相似，随着频率的增加都是先减小后增大，在4 THz左右时最小。而湮灭过程一直在增加。结合前文讨论，随着频率增加声子群速度降低，湮灭通道数增加，故声子寿命减小，说明声子散射在加强，在4 THz左右达到最强。大于4 THz后LA声子支明显具有相对较大的P3，增加了a+a↔o和a+o↔o散射通道的数量，这与LA声子支弛豫时间较长一致。

从图9(b)看出，ZA声子支的吸收过程比湮灭过程大了接近两个数量级，这说明声子散射过程中ZA声子极易与其他声学声子支声子发生碰撞后湮灭，阻碍了声子传递热量，即产生所谓的热阻。

2.4 晶格热导率的尺寸效应分析

对于真实材料而言，材料的尺寸大小对其热导率有重要的影响。材料的声子扩散输运和弹道输运的尺寸效应与其平均自由程(mean free path, MFP)有很大关系，而探究声子平均自由程必然联系到累积晶格热导率。所谓累积晶格热导率，就是将所有的MFP或者频率对热导率的贡献进行累加后得到的热导率。本文深入研究了WS2的声子平均自由程和频率对其累积晶格热导率的影响规律。

累积晶格热导率κacc和声子平均自由程MFP的关系，可用公式(2)[32]来拟合：

(2)

式中：κmax表示最终(最大)累积热导率值；lMFP表示声子平均自由程；lmax表示最大声子平均自由程；l0表示可承载热量的声子的平均自由程，也称为临界MFP，即所要评估的参数。

图10分别给出了在不同温度(300、450、600 K)时累积晶格热导率κacc随平均自由程MFP和频率的变化规律曲线。

从图10(a)可以看出，累积热导率κacc随平均自由程MFP先迅速增大后保持不变。以300 K时为例，声子平均自由程MFP大于6.5 μm时WS2的累积热导率κacc不变，说明导热贡献均来自MFP小于6.5 μm的声子。用虚线拟合后，得到了300、450和600 K下的l0(临界声子平均自由程)，分别为553、380和261 nm。当材料的特征尺寸远小于这些临界声子平均自由程时，声子几乎不受散射，那么该输运过程应为弹道输运。这对纳米结构的热设计至关重要，因为此时的热导率可以通过改变纳米结构而进行有效调节。由此可见，声子临界平均自由程对设计低热导率微纳电子器件具有重要的参考价值。

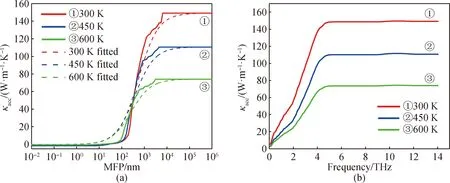
图10 不同温度下单层WS2累积晶格热导率随MFP(a)和频率(b)的变化关系曲线

图10(b)给出了累积晶格热导率κacc与频率的变化规律曲线，可以看出三个温度(300、450、600 K)下三条曲线的κacc都随着频率的增大而迅速增大，达到峰值后就不再依赖频率，这说明低频的声学声子对热导率具有全部的贡献。图10(b)中的三条曲线的拐点几乎一致，说明声子频率对热导率的贡献并不受温度变化的影响。