协作机器人参数辨识与误差补偿算法研究

秦 蒙，陈良培，孟琨泰

(1.重庆电力高等专科学校 信息工程学院， 重庆 400053；2.中国科学院深圳先进技术研究院 光电工程技术中心， 广东 深圳 518055；3.河北机电职业技术学院， 河北 邢台 054000)

0 引言

随着市场经济的快速发展，个性化定制的市场体量正在日益扩大，实体工业生产模式正在从大批量、单一化的刚性生产线向着小批量、多样化、定制化的柔性生产线转变。工业企业对机器人的需求不再局限于单一重复性的作业，而是希望机器人能够在多元化工作场景中像人一样快速转换完成各类复杂任务。因此协作机器人应运而生，它可以在指定协作区域内与人进行交互作业，具有安全性高、通用性好、易于编程使用的特点[1-2]。

目前市场上的协作机器人的构型大多采用7自由度的串联式冗余机械臂构型。串联构型的7R协作机器人长悬臂、大负载的限制，使得机器人刚柔耦合变形误差较大[3-5]。另外，考虑制造误差、加工误差、控制器控制误差以及温度场等外界使用环境的影响使得冗余构型的协作机器人末端执行器的位置误差较大，绝对定位精度较低，严重影响了协作机器人的高精度定位作业和人机协作、人机共融的发展。

协作机器人作为典型的多输入多输出的非线性时变动力学系统，在工作过程中往往要承受非线性摩擦、可变载荷、外界未知干扰、多物理场等的动态干扰。针对协作机器人串联多关节的结构特点，传统的控制策略主要有自适应控制、神经网络控制、滑模控制(SMC)和变结构控制等[6-10]。其中滑模变结构控制因具有较强的鲁棒性和对非线性、不确定动态和有界输入扰动不敏感的特点，被广泛应用于非线性系统的逼近。Yen等[11]研究了柔性机械臂在未知扰动下的期望轨迹跟踪的非线性控制算法，基于欧拉-拉格朗日法推导了机械手的动力学方程，设计了非线性控制律[12]。Soltanpour等[13]提出了一种简单的模糊滑模控制方法来实现对机械手的轨迹跟踪。

考虑协作机器人刚柔耦合使得末端执行器产生较大的绝对位值误差，单纯的设计控制器将无法实现高精度轨迹跟踪，必须对其进行非线性系统辨识[14-17]。目前，多场耦合柔性体系统往往呈现高度非线性、强耦合的动力学特性，且某些耦合因素对动力学行为的影响并不明朗，导致动力学模型存在未知部分，加深了协作机器人动力学系统的非线性，影响末端绝对位置精度。针对机器人位置精度提高的方法有2种：误差预防法和误差补偿法[16]。误差补偿法相比于误差预防法，成本低且补偿效果明显，是降低机器人位置误差的重要途径。常用的误差补偿方法有运动学标定和非运动学标定。运动学标定主要解决的是运动学建模时DH参数误差(几何误差)，非运动学标定主要解决机器人的非几何误差，包括机器人杆件和关节的柔性变形、末端可变负载、温度场等外力场引起的变形、变速齿轮的传动误差等。对于协作机器人大负载搬运应用领域，非几何因素是影响机器人轨迹和定位精度的主导因素之一，因此进行协作机器人非几何误差的辨识极具实际应用意义。

针对机器人系统参数误差辨识的问题，Gao等[18-19]基于BP神经网络改进的粒子群优化算法进行工业机器人的参数辨识。Nubiola等[20]考虑所有可能的几何误差和位姿参数，采用最小二乘技术和大量实验优化了ABB 1600型机器人末端位置误差。 Madsen等[21]将已知的逆动力学辨识模型与刚性机器人非线性动力学的加权最小二乘模型相结合，通过降低建模误差来提高标定精度，有效补偿了转子惯性力矩和非线性摩擦力。Qiao等[22]采用基于指数公式乘积的标定方法，通过伴随变换来表示2个扭转之间的变换关系，仅依赖于参考构型，通过一次标定即可获得机器人的精确运动参数；王一等[23]通过建立柔性关节的弹性扭簧模型，将柔度误差分解为外加负载柔度误差和机械臂自重柔度误差分别进行补偿。

刚柔耦合状态下的柔性关节、柔性杆的变形误差、控制器控制误差、末端变载荷变空间位姿下的变误差的影响使得协作机器人末端执行器的轨迹跟踪误差较大。为了解决这些问题，以库卡LBR协作机器人为例进行分析，基于网格化工作空间原理和线性化可变负载模型对协作机器人进行变参数误差补偿，基于有限元软件建立协作机器人刚柔耦合模型，并利用ADAMS-Matlab/Simulink联合进行协作机器人误差分析与变参数补偿算法验证，提高末端执行器轨迹跟踪精度。

1 协作机器人运动学与动力学分析

1.1 运动学建模

协作机器人正向运动学模型是进行绝对位置误差标定的基础。为了直观地表述协作机器人关节空间位置，将各关节的坐标系建立在对应的关节轴上，如图1所示。

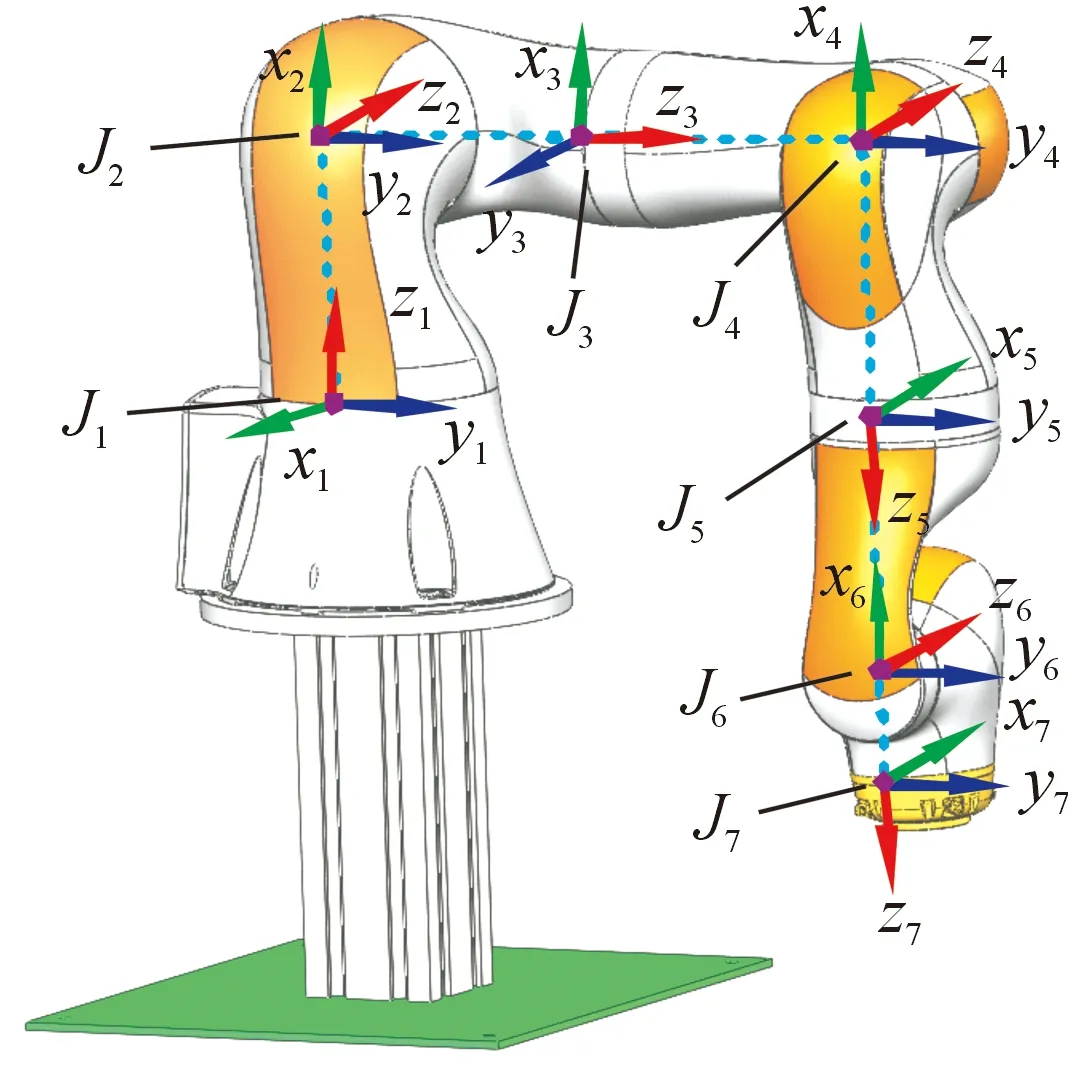
图1 库卡LBR协作机器人坐标系示意图

正向运动学建模方法采用改进后的DH模型建立，具体参数如表1所示，相邻两连杆之间的齐次坐标变换矩阵为：

(1)

式中:ai,bi,ci为连杆偏距;θi,αi,βi为关节转角共同组成改进后的DH参数。

则协作机器人末端负载相对于基坐标系的位置关系可以表示为：

(2)

表1 LBR协作机器人改进的DH参数

1.2 动力学建模

通过拉格朗日方程建立机器人刚柔耦合动力学方程。库卡LBR协作机器人是典型的串行多关节机械臂，最终动力学模型表示为：

(3)

用拉格朗日方程展开式(3)可得任意关节p的扭矩为：

(4)

式中：L=K-P为拉格朗日函数，表示蛇机器人动能K与势能P之差；Ii为伪惯量矩阵；mp为连杆质量;mgp为负载质量。

2 协作机器人控制系统建立

进行协作机器人参数辨识不但需要考虑几何和非几何参数的影响，控制误差也是不可忽略的因素之一。协作机器人的控制目标是设计一个稳定的控制器，使各关节输出轨迹q快速准确地跟踪期望轨迹qd，即保证跟踪误差e在有限时间内收敛到零。基于1.2节协作机器人动力学方程的特点，设计了一种基于RBF神经网络的滑模自适应控制器(RSMC)，原理如图2所示。

图2 神经网络滑模自适应控制原理示意图

对协作机器人动力学方程式(3)进行滑模控制器设计，假设理想角度为qd，误差为e(t)=q-qd，则可设计滑模控制律为：

(5)

式中:u为反馈控制律。将式(5)代入式(3)可得到：

(6)

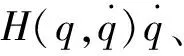
针对以上特点，并结合神经网络的万能逼近特性，可以逼近外界干扰及不确定性，并加以补偿。因此可采用RBF神经网络与滑模控制结合实现上述不确定性系统的控制。

神经网络由于其固有的逼近能力，被广泛用于逼近未知非线性曲线[24]。用RBF网络逼近一个连续函数Vi(X)∶Rq→Rp可以表示为：

Vi(X)p×1=WTh(Xin)+ε(Xin)

(7)

式中：Xin=[x1,…xn]是网络输入；W∈Rp×q是网络权值；n>1,是神经元数量；[h1(Xin)…hq(Xin)]T∈Rq为高斯基函数；ε(Xin)为网络逼近误差。

高斯RBF神经网络基函数h1(Xin)网络算法为：

i=1,2,…，n

(8)

式中：Ci,bi为第i个神经元的中心和宽度。

(9)

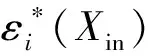
3 参数辨识及误差补偿算法

3.1 矩阵微分法误差建模

机器人在关节空间内的参数误差因连杆柔性、关节柔性、自重、负载和电机控制等因素的影响，呈现出不均匀分布的特点。对于协作机器人，由于各关节参数存在误差，根据微分变换法对相邻连杆间的坐标变换进行全微分可得：

(10)

由于关节参数存在误差，末端坐标系相对于基坐标系的齐次变换矩阵为：

(11)

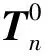
(12)

可得协作机器人末端位置偏差ΔP为：

ΔP=PR-PN=BΔη

(13)

为求解式(13)中的参数误差值，需要引入多个采样点：

(14)

式中，n为采样的个数。

协作机器人在关节空间内的参数误差因连杆的柔度、关节的柔度、控制器控制误差、自重、负载的变化而变化。随着协作机器人关节空间内转角的变化，关节转角会产生一定误差，但同时伴随着连杆柔度误差、控制器控制误差，其他参数也会产生一定程度的变化[26]。因此，协作机器人的各个参数误差均可以表示成关于关节空间内关节角的函数：

Δη=(Δθ,Δα,Δa,Δd)=f(θ1…θ7)

(15)

式中：Δη表示参数误差的集合。因为协作机器人各关节转角θ1…θ7相互耦合，难以建立关节空间内的误差模型，因此可以将协作机器人关节空间内的确定空间位姿转换到工作空间进行求解：

f(θ1…θ7)=g(x,y,z)

(16)

3.2 工作空间变参数误差补偿

由式(15)、(16)可知，给定关节空间或者工作空间内的一组位姿参数就可以确定该位姿下的协作机器人参数误差Δη。协作机器人末端执行器在工作空间中的位姿变化较大，各个空间位姿下的连杆柔度、关节柔度、控制器控制误差、自重等非几何因素造成末端执行器位置误差分布不均。另外，协作机器人末端承受十几千克可变负载，对末端执行器的位置精度也具有较大影响。因此，采用单一的固定参数误差集合Δη补偿整个工作空间内的位置误差时，协作机器人末端执行器的绝对位置精度提升有限。

采用对协作机器人工作空间进行网格化的变参数误差补偿方法，如图3所示。对工作空间进行网格划分，依次辨识各个网格内的参数误差Δηi，从而提高协作机器人末端执行器在整个工作空间内的绝对定位精度。针对协作机器人工作空间内的单个网格，如图 3所示，末端负载恒定时，协作机器人所受连杆柔度、关节柔度、控制器控制误差、自重等非几何因素影响非常接近，因此在小范围内牺牲一定程度位置精度的前提下，可采用单一参数误差集合Δηi进行误差补偿。当负载变化时，在单个网格内协作机器人可以简化为线弹性悬臂梁结构(忽略随机误差的影响)，因此其末端的位置误差可以等效为：

Δx=kamg+Δx0

(17)

式中：Δx为空间位置误差；ka为位置误差系数；Δx0为零负载下的位置误差。

图3 工作空间网格化原理示意图

同理，可以得到关节空间内变负载下的一组参数误差矩阵为：

(18)

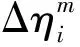
根据上述分析可知，单个网格划分得越小，协作机器人所受连杆柔度、关节柔度、控制器控制误差、自重等非几何因素影响越接近，单个网格内的协作机器人线弹性悬臂梁结构相似度越高，从而末端执行器在整个工作空间内的绝对定位精度越高。

3.3 参数误差求解流程

采用非线性阻尼最小二乘算法中的Levenberg-Marquardt (LM)算法进行协作机器人参数误差求解。LM 算法是使用最广泛的一种优化算法，其最终目标是寻找一组使函数具有最小值的参数向量，是利用梯度来求极值的算法。相较于高斯牛顿法与梯度下降法，LM算法既有梯度下降法的全局搜索、快速寻优的能力，也具有高斯牛顿法的快速收敛到最优解的能力，在处理冗余参数问题时具有独特的优势，在参数求解时能有效避免陷入局部最优，处理复杂问题的效率也较高。

高斯牛顿法的迭代式为：

xk+1=xk+hgn

(19)

xk+1=xk+H-1▽f

(20)

(21)

式中：▽f为雅可比矩阵;H为海塞矩阵。因此：

(22)

Levenberg-Marquardt算法是对高斯牛顿的改进，在迭代步长上略有不同：

(23)

根据机器人具体结构和理论结构参数对雅克比矩阵及其他参数进行初始化，ε>0，α1>m>0，0≤p0≤p1≤p2≤1，k=1。LM算法的每次迭代主要包括5部分：

步骤1建立目标函数，根据式(39)可得ΔP=PR-PN=BΔη，式中ΔP为末端空间位置偏差；Δη为待求的参数误差向量；

步骤2 根据机器人具体结构和理论结构参数对雅克比矩阵及其他参数进行初始化，确定寻优初始值Δη，终止控制常数ε≥0，并根据初值Δη计算第k次迭代时的当前空间位置误差ΔP；

步骤3根据第k次估计值计算第k次迭代时雅可比矩阵J(xk)；并利用阻尼最小二乘法求解参数误差矩阵：

Δxk=-(JT(xk)J(xk)+λkI)-1JT(xk)ΔP(xk)

(24)

式中：k表示迭代次数；Δxk表示第k次迭代时的参数误差改变值；xk表示第k次迭代的参数误差；λk表示第k次迭代时的阻尼因子。

(25)

计算更新参数误差矩阵后第k+1次迭代时的机器人当前空间位置误差:

ΔP(xk-Δxk)=PR-PN(xk-Δxk)

(26)

计算第k次迭代时实际下降量ΔFk与预估下降量ΔLk的比值qk:

(27)

(28)

定义实际下降量ΔFk和预估下降量ΔLk的比值qk来监控步长的质量：

(29)

步骤4更新迭代参数。

预估下降量ΔLk>0是人为构造，因此，若qk很小或者为负值，说明迭代失效，此时xk+Δxk不能作为下一个迭代点，须增大阻尼因子λk、减小步长xk-Δxk，进行重新求解以便下次迭代时更接近于梯度下降法。实现全局搜索；若qk很大，此时迭代有效，可以减小阻尼因子λk，增大步长xk-Δxk，以便下次迭代时算法更接近高斯牛顿算法，实现快速收敛到最优解，其他情况下阻尼因子λk与迭代步长不变。由此可得第k次迭代参数更新法则。

第k+1次参数误差矩阵更新法则：

(30)

第k+1次阻尼因子更新法则：

(31)

k=k+1

(32)

4 仿真验证

为了验证RSMC控制器对协作机器人刚柔耦合模型轨迹跟踪精度，以及LM变参数误差补偿算法的效果，在Matlab/Simulink环境下对RSMC控制器进行建模，并结合ADAMS动力学分析软件建立协作机器人三维动力学模型，利用ANASYS软件有限元软件对协作机器人刚性连杆进行柔性化处理实现刚柔耦合联合仿真。协作机器人基座连杆变形较小，剩余连杆为铝合金材料变形较大，设定第一关节后的铝合金连杆弹性模量70 GPa，泊松比为0.3，进行柔性化处理，可得如图4所示机电一体化仿真模型结构。刚柔耦合的变形结果如图5所示。

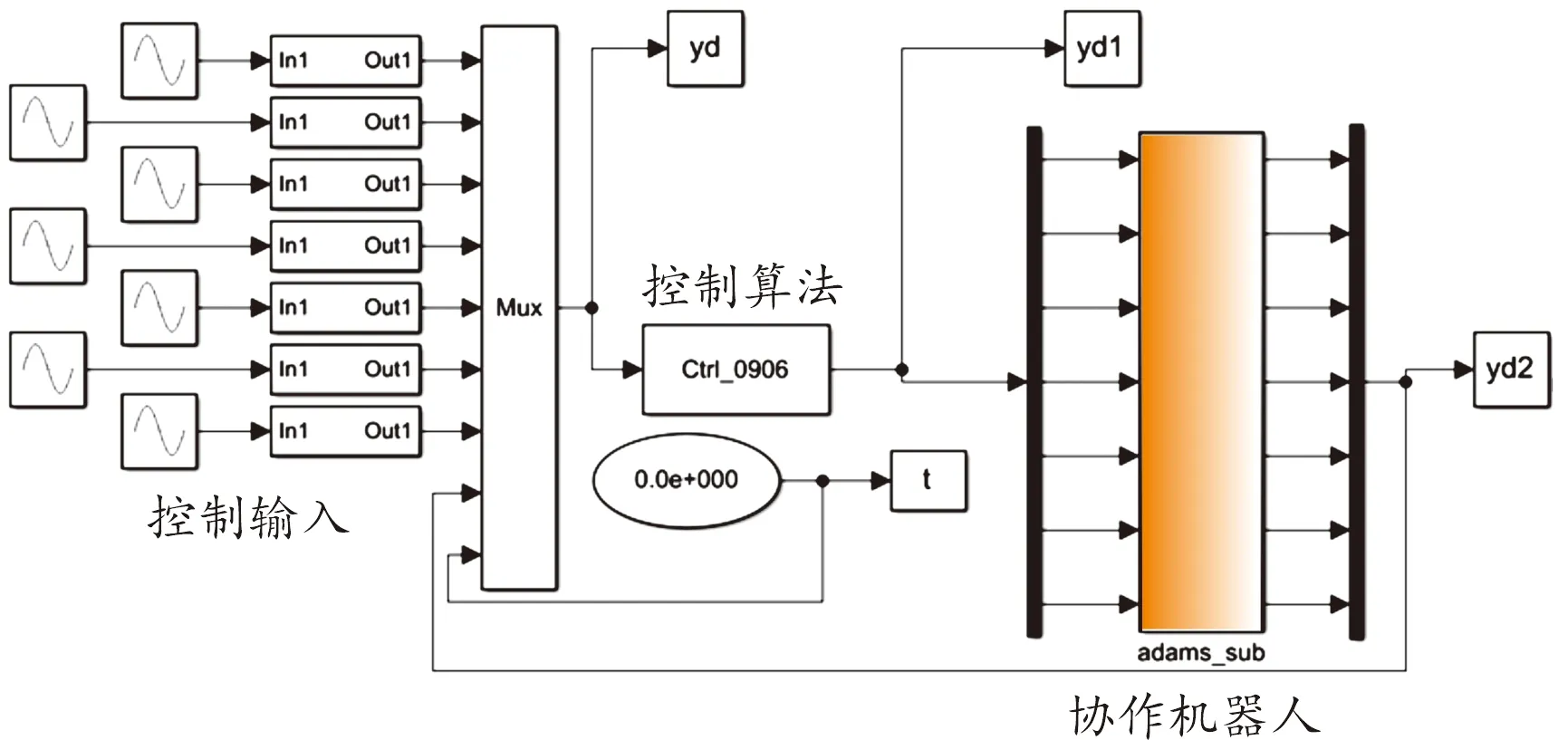
图4 协作机器人机电一体化仿真模型结构

图5 刚柔耦合的变形结果

4.1 RSMC控制器控制效果

给定关节2正弦曲线控制信号如图 6(a)，设定末端执行器不同负载(0～6 kg)进行RSMC控制器控制性能仿真，仿真时序如图5所示，结果如图6所示。分析结果可得：仿真过程中关节扭矩输出平稳，仅起始阶段存在阻尼振荡；极限工况下关节角位移最大跟踪误差约为0.008 rad，平均角位移误差约为0.000 1 rad，末端执行器沿Z轴最大位置误差约为7 mm，平均位置误差约为 4.7 mm，主要来自于协作机器人柔性连杆自重和末端负载引起的沿Z轴的位置误差。总的来说，设计的RSMC控制器性能较好，位置误差较小。

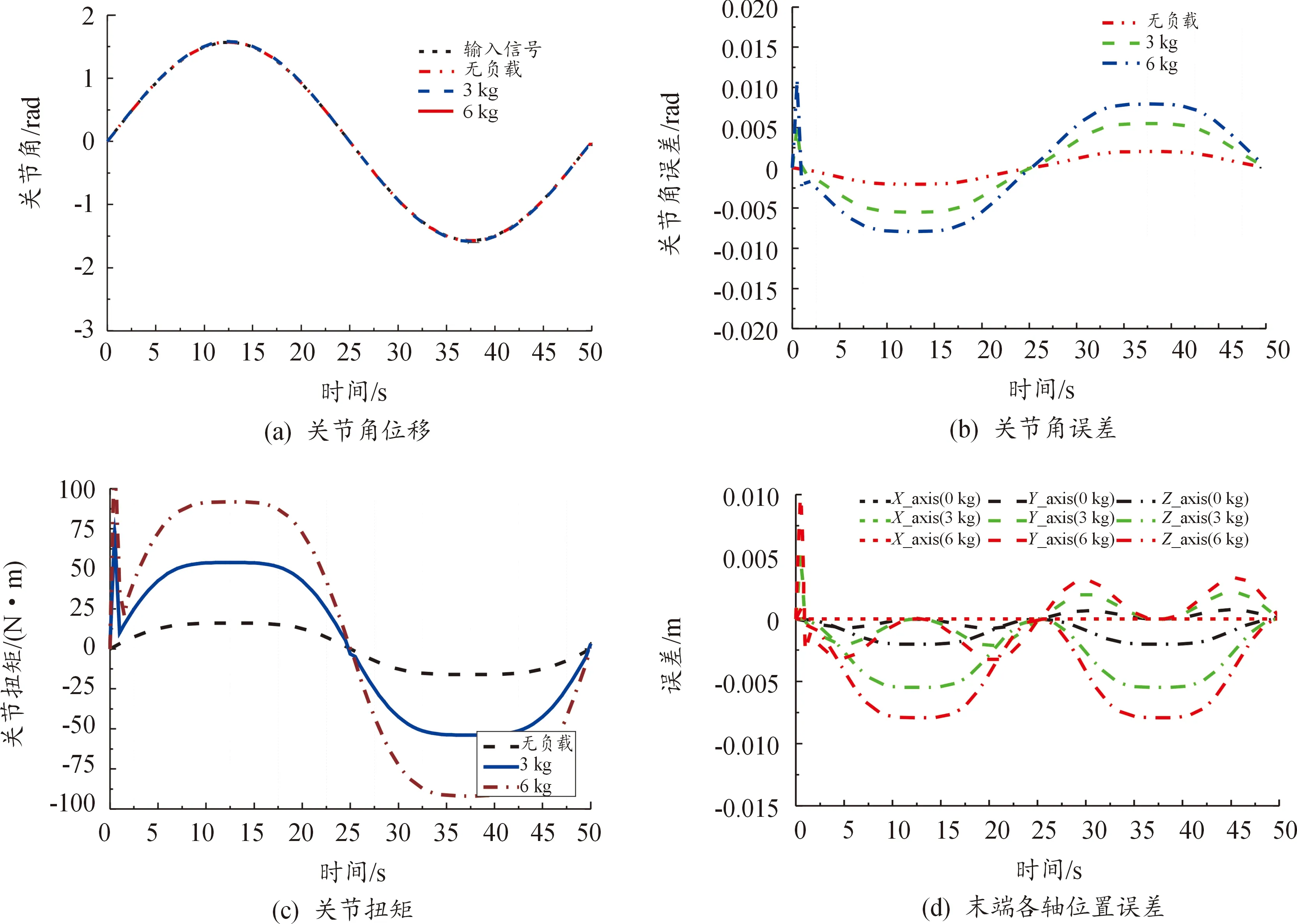
图6 基于RSMC控制器协作机器人刚柔耦合仿真结果

4.2 LM算法位置误差补偿修正

将协作机器人工作空间沿基坐标系Y轴均匀分成1、4和8份，分别利用LM算法、网格化工作空间和线性化可变负载模型进行变参数误差补偿。不同末端负载下(0～6 kg)各网格化的工作空间内补偿参数如表2、3所示，将补偿参数代入RSMC控制器重新仿真，结果如图7—9所示。负载越大，关节角误差、末端位置误差越大。补偿后协作机器人极限工况下关节角平均误差小于0.002 rad，沿Z末端平均位置误差小于0.2 mm，大大降低了末端位置误差补偿，效果明显。图7—9中，在起始、终止以及中间时刻(25 s)的位置误差较大，主要是该区域误差值的变化范围较大、网格化工作空间较为稀疏导致，可进一步细化网格以提高位置精度。

4.3 线性化变负载补偿

将同一空间网格下不同负载的参数误差补偿值绘制成曲线图，如图10所示，发现同一空间网格不同负载下的参数误差补偿值与负载成线性关系。通过计算斜率即可得到各种负载质量下的位值误差补偿值。

表2 工作空间4网格位置下的补偿值 rad

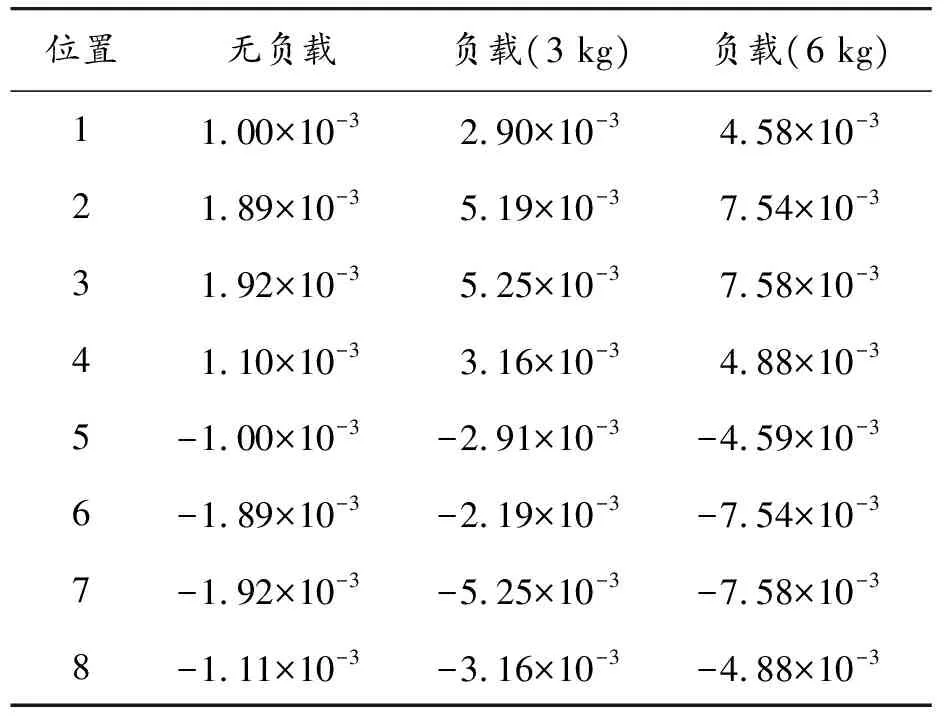
表3 工作空间8网格位置下的补偿值 rad

图8 协作机器人3 kg负载变参数误差补偿结果

图9 协作机器人6 kg负载变参数误差补偿结果

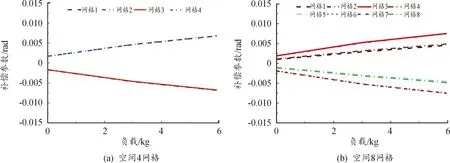
图10 线性化可变负载补偿

5 结论

基于协作机器人刚柔耦合动力学模型，设计了一种基于RBF神经网络的滑模自适应控制器。通过ADAMS-Matlab/Simulink联合仿真验证了控制器的效果。分析了协作机器人刚柔耦合模型极限位姿下的轨迹跟踪误差。结果表明：极限位姿下协作机器人刚柔耦合模型末端执行器位置误差极值约为7 mm，平均误差约为4.7 mm。其误差来源主要是控制误差、悬臂状态下沿Z轴负载及自重造成的协作机器人杆件变形误差。为了补偿位置误差，基于L-M非线性阻尼最小二乘法，结合空间网格和线性化可变负载模型推导了协作机器人工作空间变参数误差补偿算法。通过联合仿真验证了轨迹跟踪误差补偿效果，结果表明，变参数误差补偿算法大大降低了协作机器人极限位姿下的轨迹跟踪误差，极限位置下的平均位置误差小于0.2 mm。其中，起始、终止以及中间时刻(25 s)的位置误差较大，该区域误差值变化较大，通过细化网格密度可进一步提高位置精度。所提方法可为协作机器人控制器的设计和刚柔耦合模型位置误差补偿的研究提供参考。