基于增量宽度学习的投资组合风险控制模型

陈良霞 李 博， 王 琪 余 远 冯泽涛 贾 颖

（1.山东工商学院 计算机科学与技术学院，山东 烟台 264005；2.山东工商学院 统计学院，山东 烟台 264005）

一、引言

投资组合是对各种金融资产进行资金的最优配置[1-2]，目标是在风险最小化的同时产生稳定的收益。除了金融，投资组合选择还在多个领域得到广泛研究，如人工智能、机器学习和统计学等。传统的投资组合选择方法通常来源于两种经典的方法：马科维茨均值方差模型[3]和凯利理论[4]。由哈里·马科维茨提出的马科维茨模型基于均值-方差组合选择框架，适用于单周期投资组合选择。而凯利资本增长理论关注的是多期投资组合选择和预期收益最大化，但没有考虑风险控制。随着高性能计算机的发展，这两个理论引起了研究人员越来越多的关注，在线投资组合选择也成为近几年投资组合研究领域的热点。

近年来，研究人员开发了很多新的投资组合选择策略，特别是针对在线投资组合[5]。这些模型适用于在线场景，因为它们不仅具有实时交易特性，而且侧重多期投资组合选择。在线投资组合进行的实时交易需要投资者作出决定和调整资本分配，以产生较高的财富回报。

根据在线投资组合选择的具体应用，交易策略被分为四类[6]。第一类称为基准模型。相应的策略包括统一买入并持有（UBAH）、最佳股票（Best Stock）、统一恒定再平衡（UCRP）和最佳恒定再平衡（BCRP）。统一买入并持有策略在交易期开始时购置资产，并将资产配置推迟到交易期结束。最佳股票策略是买入并持有策略的一个子模型，在该策略中，最好的股票是通过追溯历史获取的。统一恒定再平衡策略是一种固定比例的策略，用于在每个期间开始时重新平衡预设的投资组合。而最佳恒定再平衡策略是一种恒定再平衡的投资组合策略，在该策略中，根据交易日的结果对投资组合进行修改，以使累积财富最大化。第二类称为“追随赢家”，因为它试图渐近达到与最优策略相同的增长率。这些方法假设之前成功的股票将在接下来的一段时间内仍然表现良好。第三类是“追随失败者”，它基于这样一种观点，即当前时期的赢家在下一时期可能不会成功。虽然这一想法似乎缺乏依据，但在实际交易环境中，这一策略往往会取得优异的表现。

由于前三个类别中的模型不挖掘数据集上的隐藏模式，第四类（模式匹配策略）试图基于相似的历史模式和趋势预测资产在特定时间窗口内的后续分布。该策略假设相似的历史模式将产生相似的结果，然后作出相应的决定。此外，最近几年的一些研究工作结合了互联网上不同利益相关者的信息和每日价格来预测股票收益[7]。在机器学习模型流行后，导致了人们对投资组合选择的兴趣与日俱增。然而，以上模型没有考虑增量学习和系统风险。考虑到市场的不确定性，如庄家操作等因素，仅利用模式识别方法是不够的。此外，尽管这些在线投资组合选择模型是多样化的，但它们都未将资产波动视为风险。

针对上述问题，本文提出了一种新的收益-风险控制模型。首先，本文提出了一个增量宽度学习模型，该模型以增量的方式进行在线学习，比目前提出的其他模型更灵活。其次，基于随机矩阵理论[8-10]，本文提出了一种消除系统风险噪声的方法。最后，本文没有像其他很多文献一样使用每日收盘价，而是使用了30分钟和60分钟的高频交易数据。因为这样选择不仅符合实际情况，而且使用每日收盘价作为样本数据集的研究还忽略了一个关键因素——股票每日价格的波动性。

二、投资组合概述

投资组合问题可以表达如下：考虑金融市场中的各种资产，用价格向量p=[pt1，pt2，…，ptm]T来表示tth时期的价格，其中t=1，2，…，n，n表示周期数，m表示资产数即相对价格向量的维数。如前所述，该周期为30或60分钟的短间隔。m维相对价格向量由xt∈Rm表示，其中xt=pt/pt-1。在第t个周期开始时，将资产分配给投资组合向量bt。bt的第ith个元素（bti）表示投资于第jth种资产的资金比例。因此，每个投资组合都应该满足约束：bt∈{b：b≥0，bt1=1}。投资者可以使用过去时期的历史数据在这段时间内重新配置bt，将投资组合维持到收盘时间。因此，收益St将增加因子btxt，其初始值为S0=1。在n个周期后的最终累积财富可表示为：

通常，在线投资组合选择的主要目标是通过使用统计或人工智能模型开发新的投资组合策略，以实现累积财富的最大化。投资者必须同时使用适当的指标将风险降低。投资组合算法整体框架见算法1。

算法1.在线投资组合框架1.第1步：初始值b1和S0=1 2.第2步：输入历史相对价格序列xt∈R+m 3.第3步：For t=1，2，…，n 4.从市场获取相对价格xt 5.计算周期返回btxt，并更新累计值St=St-1×btxt 6.设置更新投资组合模型7.使用模型学习投资组合bt+1 8.End for 9.第4步：输出最终的累积财富等指标

三、模型简介

（一）增量宽度学习系统

宽度学习的模型架构见图1[11]。该算法的输入是一个相对价格矩阵X∈Rm×k。其中k是周期窗口长度，其相应的输出是预测的相对价格向量。令Zi是ith的映射特征，Hi是ith的增强征，则A=[Z｜H]是块矩阵。宽度学习模型可以表示为AW=Y的映射，因此有W=A-Y，其中Y是标签矩阵。本文在宽度学习的基础上提出了一种增量宽度学习模型，可以在增强特征方向进行维度扩展。考虑增强特征的维度扩展，Ah=[Z｜H1…h]则可以表示为：

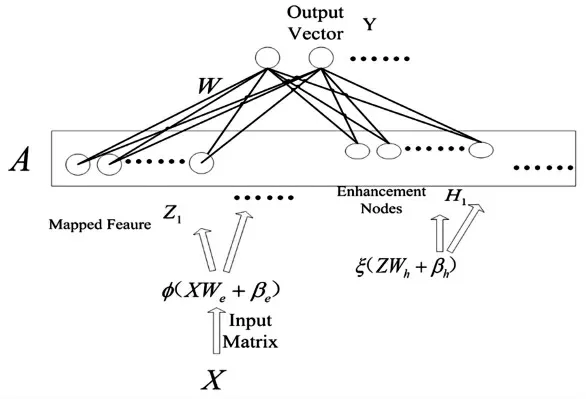
图1 宽度学习架构

其中，A2=A+BBT+BDBT和B2=B（I+）。由此可得：

其中，

图1 中，φ是线性函数，ξ是线性或非线性函数，We和Wh是正态分布的权重收益率。宽度学习模型不需要使用反向传播算法来更新权重。因此，可以独立设置映射特征和增强节点的数量Ah+1的广义逆的特殊解可以表示如下：（（Ah+1）TAh+1）-（Ah+1）T，则有：

令A=（Ah）TAh，B=（Ah）THh+1，D=（Hh+1）THh+1，则有：

其中，C1、C2、C3、D2由式（4）定义。新的权重由下式得出：

因此，该模型可以通过增量学习来学习到新的权重。本文使用宽度学习的目的是在均值方差模型中产生价格序列并消除系统风险。它使用协方差作为风险控制因子，该因子由使用之前的历史数据计算得出。

（二）Bootstrap方法

Bootstrap方法用于扩展预测数据矩阵。假设增量宽度学习模型产生了一个相对价格矩阵Xp∈RM×K，它可以扩展到Xp∈RM×K（N×M），相关矩阵Cp可以通过XP确定。

（三）风险控制模型

本文中，我们提出了一种新的风险控制模型，如式（8）：

其中，E（rp）代表投资组合的平均回报，b是投资组合向量，x是平均相对价格向量，σ是投资组合方差，δ1和δ2是不同风险比重系数，∑是资产的协方差矩阵，由预测的相对价格序列计算而得。函数lg（·）的作用是对结果的放缩。目前一些研究工作的重点是改进方差，使用随机矩阵理论分析资产相关性，并将随机噪声视为系统风险或外部市场影响。然而，这些研究并没有利用预测数据从协方差矩阵中去除噪声。

（四）完备性

其中，μi和σi分别是xi的均值和标准差。因此，CP可以通过XP直接计算。

需要注意的是，在计算协方差的过程中，随机矩阵需要满足M→+∞和N→+∞。但是，这个条件是不切实际的。因此本文虽然采用了Bootstrap方法，但还需要提供样本和总体协方差的估计。给定特定样本（x和y）和总体（X和Y），样本均值可以表示为和总体均值可以表示为E[X]=μx和E[Y]=μy。另外，和是无偏估计，且能够得到：

其中，xi和yj是成对数据。因此：

因此样本协方差的期望可以表示如下：

根据推导结果可知，在本文研究背景下，样本协方差是总体协方差的无偏估计。这种完备性在前述文献中未探讨过。

四、实验结果

（一）数据集获取

本研究中使用的数据集见表1。选择的股票数据集来源于深圳证券交易所的3个不同指数：中小企业板创新指数（SMEBII）、创业板创新指数（GEBII）和大数据50指数（BG50I）。每只股票采集两种不同频率的数据（每30和每60分钟的股票价格变动）。例如，SMEBII-30min数据集中的股票价格是中小企业板创新指数中每只股票每日每间隔30分钟期间内的收盘价。

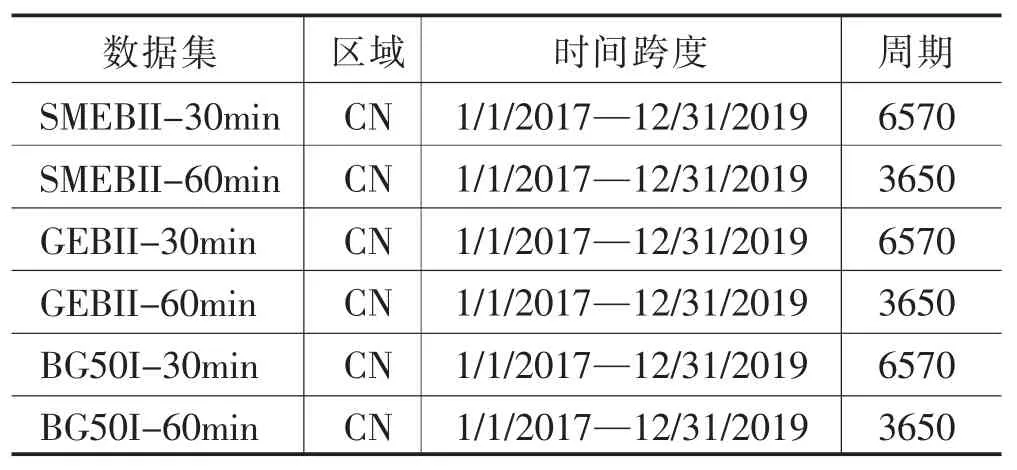
表1 使用来自深圳股票交易所的6个真实数据集

考虑到时间成本和资产的管理成本，我们每个指数选择了20只股票，3个指数共60只股票。因此，本文采集了来自3个指数、2种频率的60只股票的高频价格数据构成了本文使用的全部6个数据集。

（二）评价指标

本文用5个不同指标评估所提出的方法。

1.特征值分布，用于比较和预测随机相关矩阵的特征值的相似性。

2.累积财富（CW）[15]，描述了在特定时间段内获得或损失的总投资的累积回报。如前述章节所述，CW是评估模型性能的最重要指标。

3.夏普比率（SR）[16]，描述了每个波动期（投资组合的标准偏差）超过无风险利率的平均回报。它允许投资者更直接地评估与承担活动相关的风险与利润，定义如下：

其中，Rf是无风险利率，σt是tth当期投资组合权重的标准差。风险调整后的回报通常随着SR的增加而增加。

4.信息比率（IR）[17]，通常被用作衡量投资者相对于基准产生超额回报的能力。它通过在计算中加入风险标准偏差来考虑性能的一致性，定义为：

其中，Rb是基准回报。在本文的研究中，最佳股票（Best Stork）被用作基准。较高的信息比率表示较好的性能，相反较低的值表示较低的性能。

5.卡尔马比率（CR）[18]，用于确定相对于回撤（下行）风险的回报，其定义为：

（三）对比方法

为了对提出的模型进行分析和比较，本文利用4种策略对数据集进行了模拟实验。对其中一些模型进行了总结和实现。上述4种策略描述如下：

1.基准模型

最佳股票（Best Stock）：购买之前表现最好的股票。

统一买入持有（UBAH）：在开始时购买资产，一直持有资产到结束。

最佳恒定再平衡投资组合（BCRP）：将投资组合设置为事后最大化终端财富的投资组合。

统一恒定再平衡投资组合（UCRP）：在每个期初重新平衡当前投资组合的固定比例。

2.关注获胜者

在线牛顿步进法（ONS）：采用L2范数作为正则化约束项的BCRP。

3.追随失败者

置信加权均值回归（CWMR）：采用高斯分布对投资组合进行建模，并使用均值回归原理更新分布。

在线移动平均回归（OLMAR）：基于均值回归预测下一个相对价格。

4.模式匹配/机器学习

局部自适应学习（LOAD）[19]：使用局部回归来估计资产的价格趋势。

（四）特征值分布比较

本文计算了经验相关矩阵的特征值以研究其特性。图2提供了真实或经验特征值和理论特征值分布的比较。通过将经验相关矩阵的特征值与随机相关矩阵的特征值进行比较，从经验相关矩阵中提取无噪声的信息。图2表明对于同一数据集，不同频率的经验分布是相似的。然而，这些数据并不符合随机相关矩阵的理论分布。这一发现表明不同资产之间存在相关性（真实信息），并不依赖于频率。相比之下，由于两个分布之间的重叠，不同资产的相关性也存在噪声。

从图2可以看出，一些经验特征值超出了理论特征值分布，这些是与相关矩阵（真实信息）对应的无噪声特征值。因此，符合理论特征值分布的经验特征值对应于随机噪声。例如，在图2（A）SMEBII数据集中，两个频率下（30和60分钟）有35%的特征值是无噪声的。同理，在图2（B）GEBII数据集中，30分钟频率下和60分钟频率下分别有25%和35%的特征值是无噪声的。此外，在图2（C）BG50I中，30分钟频率下和60分钟频率下分别有40%和35%的特征值是无噪声的。

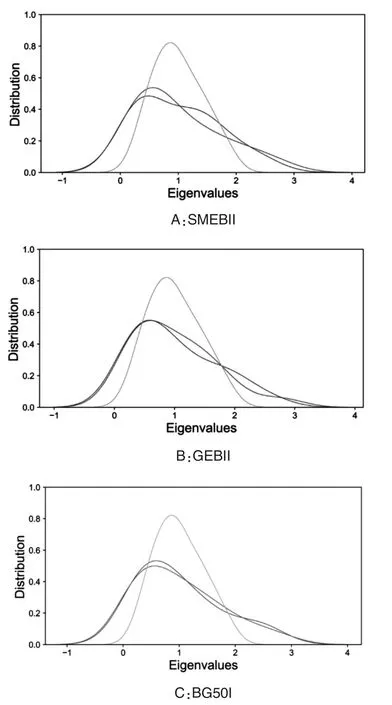
图2 不同数据集在不同频率的经验分布图

（五）累积财富

最终的累积财富结果见表2。任何一个模型都不可能在所有期间实现正的相对回报。但相对来说，一些模型例如本文提出的模型和OLMAR模型，比其他模型产生了更多的正向回报。然而，在少数期间内仅略高于1.0的相对回报可能会导致累积财富的大幅增加。因此，这一指标对于累积财富的发展至关重要。

数据结果表明，尽管本文提出的模型在BG50I-30min数据集中的领先优势相对较小，但该模型在所有数据集上都取得了最佳性能，尤其体现在以下三个数据集上：SMEBII-30min、SMEBII-60min和GEBII-60min。因此，与其他模型相比，所提出的模型可以更好地从数据集中提取统计特性或模式；此外，OLMAR（在3个数据集上排名第二）、CWMR（在3个数据集上排名第二）等模型也取得了良好但非均衡的性能；基准模型在所有数据集中均产生了较低的累积财富；机器学习模型LOAD在数据集上表现不佳。

如前所述，每个周期回报的小幅提升可以导致最终巨大的累积财富收益。例如表2所示，若BG50I-30min数据集的初始投资为1000元，应用本文提出的模型在投资周期结束时会产生约10.5万元的收益。本文研究中使用了高频数据，虽然中国股市遵循T+1交易制度，即投资者不能在一天内多次买卖，但是高频交易数据的实验使投资者可以在一天的任意30分钟之内进行一次交易。相对于其他论文中使用的收盘价，本文的实验设置更接近实际股票市场用户的交易行为，且所提出的模型产生了较高而稳健的最终累积财富（在6个数据集中均排名第一）。

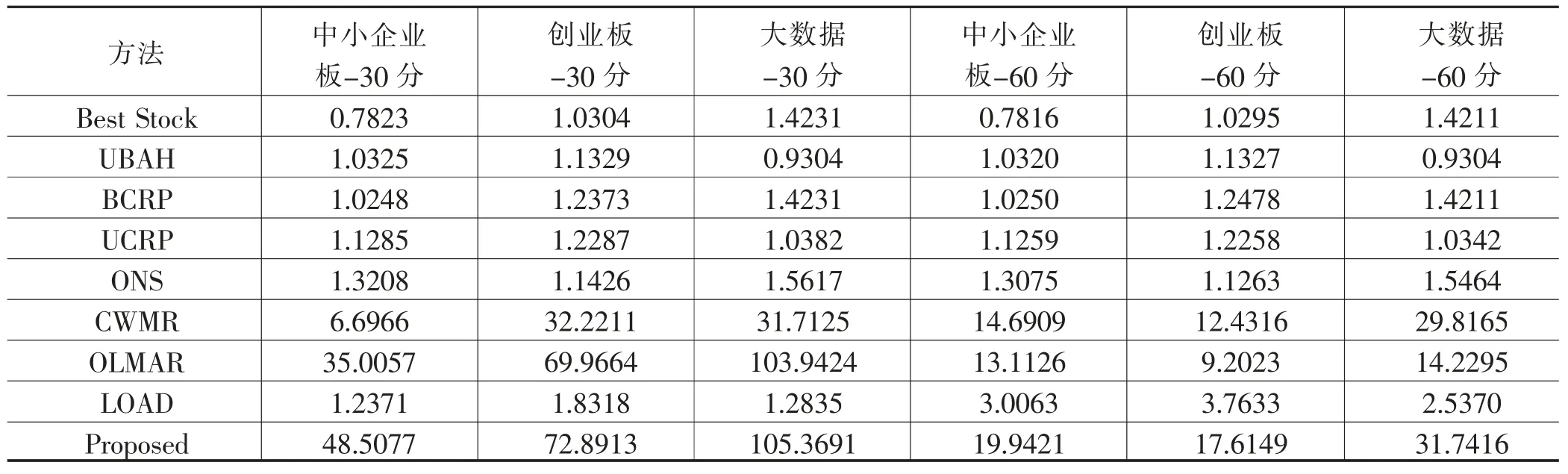
表2 6个数据集的累积财富

（六）夏普比率

在真实的金融市场中，高累积财富回报往往伴随着高风险。因此，投资者通常会尝试平衡风险与收益。夏普比率是一个重要的指标，已被广泛用于评估风险调整后的回报。表3给出了不同模型的SR计算结果。所提出的模型在所有数据集上明显优于其他模型（在所有数据集排名第一）。

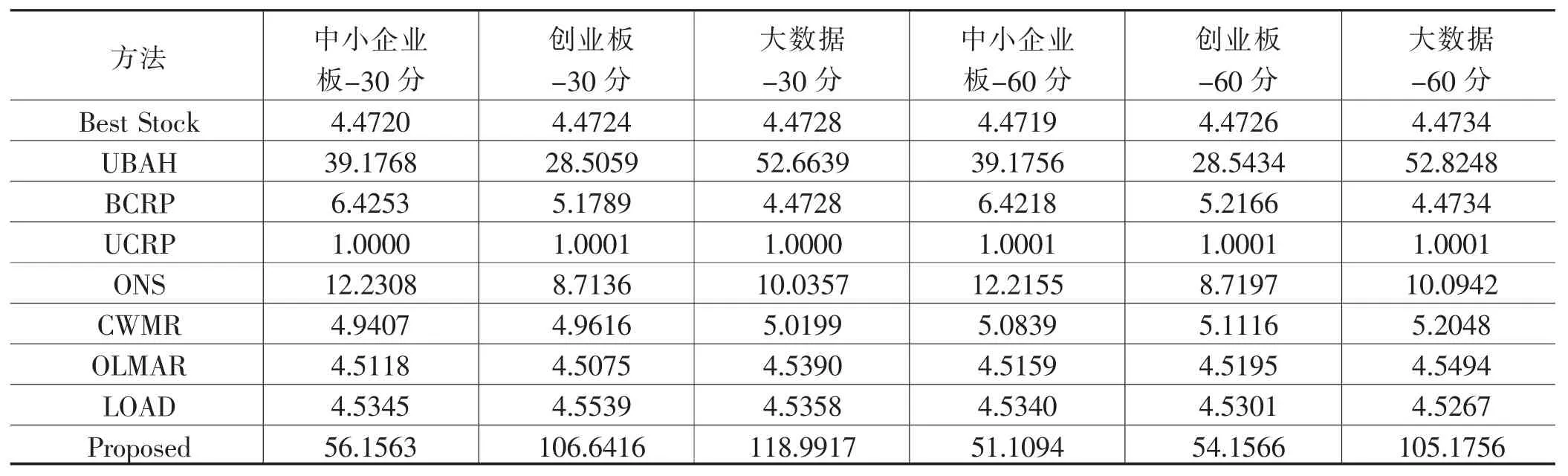
表3 6个数据集的夏普比率

（七）信息比率

表4给出了不同模型的信息比率。与夏普比率不同，信息比率用于评估相对于基准回报（不包括风险）的超额回报。实验结果表明，本文模型同样取得了最好的结果（在所有数据集中均排名第一）。其他几个模型在特定数据集上也表现良好（例如OLMAR模型和CWMR模型分别在3个数据集上排名第二）。

表4 6个数据集的信息比率

（八）卡尔马比率

卡尔马比率（CR）是用于比较平均复合回报率和最大回撤风险的指标。一般来说，卡尔马比率的值越高，模型性能越好。表5所列结果表明，本文提出的模型优于其他模型（在所有数据集上排名第一）。相比之下，其他几个模型也取得了较好效果，例如OLMAR模型（在2个数据集并列排名第一，在1个数据集上排名第二）、CWMR模型（在1个数据集上排名并列第一，在2个数据集上排名第二）。这些结果表明，本文提出的模型在卡尔马比率度量上取得了最好的效果。

表5 6个数据集的卡尔马比率

（九）运行时间

表6给出了各个模型的运行时间。从表中结果可以看出，虽然本文提出的模型耗时最多，因为它必须在每个期间训练多个BLS模型。但是，数据集是基于30或60分钟。如果本文提出的模型能够让投资者在30分钟或者60分钟内作出决策，那么模型的运行时间能够满足决策的要求。

表6 模型在6个数据集上平均一个期间的运行时间

五、分析与讨论

本研究中使用高频数据集的原因可以解释如下：（1）大多数现有研究均基于每日收盘价[20-21]，但事实上，交易者经常在每个交易日的不定时间买卖股票。尽管他们当日不能多次交易股票，但交易者可以在交易时间段的任何时间（在30或60分钟内）作出交易决定。（2）本文认为仅使用每日收盘价会忽略价格波动等关键因素，因此，使用高频数据集为训练集提供了更多信息，能更有效地预测相对价格。本文没有采用15分钟、5分钟、1分钟甚至秒级的数据，因为发现太短的时间间隔内相对价格波动性较弱。（3）由于其他研究中使用的数据集年代较久，例如NYSE（O）数据集时间跨度为1962/07/03到1962/12/31，NYSE（N）数据集时间跨度为1985/01/01到2010/06/30，SP500数据集时间跨度为1998/01/02年至2003/01/31，MSCI数据集时间跨度为2006/04/01至2010/03/31，因此本文制作了新的数据集。另外，因为存在系统风险和不确定性，仅靠模式匹配不足以分析股市中的一些股票。例如庄家的操作或者外部因素的干扰可以视为是市场噪声，这些因素都存在于真实的中国股票市场中。本文所提出的模型表现良好的主要原因是它可以进行增量学习并使用随机矩阵理论消除了系统风险。

六、结论

本研究提出了一种新的风险控制模型。首先在宽度学习系统的基础上提出了可以进行增量学习的在线学习模型。其次基于随机矩阵理论提出了一种消除噪声的方法。最后，使用特征值分布、累积财富、夏普比率、信息比率、卡尔马比率等指标来评估所提出的模型性能。结果表明，本文提出的模型在几种指标上均优于现有常用模型。因此，本文提出的模型可以在有效控制风险的同时产生高累积收益。◆