溃坝洪水演进及溃坝水流对下游坝体冲击研究

2023-03-14周昔东何小泷

中国水利水电科学研究院学报 2023年1期

周昔东，何小泷，袁浩，孙倩

(1.重庆交通大学河海学院，重庆 400074；2.重庆交通大学西南水运工程科学研究所，重庆 400016；3.重庆交通大学土木工程学院，重庆 400074)

1 研究背景

在气候变化大环境下，全球气温逐渐升高[1]，使得我国极端降雨频发，集中高频率降雨极可能导致水库溃决。溃坝导致水库库容在短时间内下泄，引发的洪水对下游建筑、河道河岸、下游大坝坝体带来巨大冲击，对于存在梯级水库的河道，极可能引发连锁反应，导致梯级溃坝。溃坝洪水不仅会严重破坏下游河道[2]以及结构物，而且会对下游的生态环境造成负面影响[3]。

溃坝实验可以直观展示出溃坝波的演进、壁面冲击压力的演化等诸多规律。研究者针对溃坝水流的演进与对建筑物的冲击开展了系统实验研究，研究内容主要集中在建筑物附近局部流场、水位的变化[4-5]，干湿河床对溃坝演进的影响[6-8]，下游结构物受到的冲击及压力演化过程[9-12]。受限于实验尺度和观测手段，实验研究并不能完全反馈出真实溃坝过程中溃坝波演进过程中的坦化和流速变化及下游建筑物所受到的真实冲击压力。而数值模拟则弥补了上述缺陷，可以获得溃坝过程中的自由液面的破碎和流场的演化过程等更为详细的流场信息。研究表明由于溃坝水流运动速度快，且在结构附近的自由水面有明显的变化，垂向压力对下游结构的影响不仅有静水压力还有冲击压力[13]。并进一步获得了不同上游库区水位条件下溃坝洪水对下游结构物附近水流流态和所受冲击压力的影响[14]。

目前针对溃坝水流实验和数值模拟研究主要集中在下游无障碍性溃坝水流演进和对下游有结构物阻挡的溃坝水流演进与冲击这两方面。由于溃坝洪水作用在结构上的冲击脉动压力的持续时间较短，这种冲击压力在许多关于溃坝水流研究中可能被低估或甚至被忽视[15]，此冲击压力虽持续时间短，但破坏性大。由于当前研究中极少考虑溃坝波与溃坝下游坝体相互作用的动态冲击过程，本文基于RNGk-ε湍流模型对三维溃坝洪水的演进及溃坝波与下游坝体的相互作用开展系统数值研究，旨在揭示在上下游不同的初始水深比α(H/h，H为上游水深，h为下游水深)条件下，下游坝体壁面受到的冲击压强峰值的变化规律及不同下游水深对溃坝洪水演进影响。

2 溃坝洪水数值模拟

2.1 计算方法简介本研究基于FLOW-3D商业软件进行数值模拟，FLOW-3D采用有限差分法对控制方程进行离散，且此次计算采用隐式方法对压力速度进行求解，其中采用的广义最小残差(GMRES)迭代法在求解大型代数方程时具有良好的收敛性、高效的计算效率和计算精度。溃坝水流演进过程可通过Navier-Stokes(N-S)方程开展模拟，其控制方程包括连续方程和动量方程：

(1)

(2)

式中：xi为坐标；ui为流体平均速度；t为时间；P为压力；gi为重力加速度；v为水流运动黏度；vt为涡流运动黏度。

由于溃坝水流计算域的尺度较大，计算历时较长，兼顾计算精度与计算资源消耗，本研究采用RNGk-ε湍流模型。其湍动能k和耗散率ε的输运方程可表述为

(3)

(4)

(5)

式中：Rε为剪切湍流附加项；G为由于平均速度梯度而产生湍流动能的产生率。本研究中湍流模型中各个系数取值为：Cμ=0.085，C1ε=1.42，C2ε=1.68，σε=σk=0.7194，β=0.012，η0=4.38[14]。

同时本研究中使用流体体积法(VOF)捕获自由液面，即在整个计算域内追踪每一计算单元的体积分数对于每个网格单元，函数F(x1，x2，x3，t)定义为流体所占体积与整个单元的体积之比，当F值为1时表示单元格体积完全被水占据，F值为0时表示单元格体积完全被空气占据。F值在0和1之间的单元表示对应于水气交接面。

2.2 模型验证及网格质量分析图1中L为计算域长度，D为水箱高度，H为水库初始水位高度，H1、H2、H3、H4为水位测量位置，图中尺寸单位均为毫米。

图1 数值模拟计算域示意图Fig.1 Schematic diagram of the calculation domain of numerical simulation

模拟结果使用h/H、P/(ρgH)、t/(H/g)1/2对水位和压强以及洪水演进时间进行无量纲化，以便后续系统地开展数值结果与实验数据进行定量对比，并采用均方根误差(RMSE)来定量评估水位数值模拟和实验测量之间的差异。由于本文重点关注溃坝水流对下游垂直坝体冲击的压强峰值，所以对数值结果和实验数据压强之间的差异采用峰值误差进行定量分析。

不同网格的数值结果与给定位置H1、H2、H3和H4实验数据水位的对比如图2所示，数值模型对波浪演化的特征提供了合理的预测，水位数值结果在二次波到来前各位置的实验数据基本一致，较准确的预测了二次波的到达时间及其在H1，H2，H3和H4位置的水位高度。受限于网格尺度，本研究中无法准确获得溃坝波冲击引起的自由表面破碎所带来的水位波动，导致数值模拟对二次波后的水位预测值与实验值差异较大，预测精度降低。水位对应的实验数据对比如表1所示，误差最大值出现在受冲击射流引起的强回流波影响最大的H4 位置，其最大误差小于14%。H2和H4位置的相对误差相对较大，造成H2位置水位误差较大其原因可能为水库水体突然下泄，下泄的水体不稳定以及闸门提升过程对水体产生影响；而造成H4位置水位误差较大其原因可能是测点靠近下游坝体墙壁，溃坝洪水到达坝体会形成壅水回流及表面破碎，引发水位振荡。

图2 数值模拟和实验的水位比较Fig.2 Comparison between numerical and experiment water level

表1 不同网格尺寸下水位均方根误差

图3展示了各点P1、P2、P3、P4的数值和实验压强值的对比。其中图3(a)展示了100次实验测试的数值压强预测和压强时间历程的置信区间，分别以97.5%和2.5%百分位水平为上限和下限[12]。数值模拟得到的压强随时间变化的过程与实验中所获一致，较好的反演了实验获得的P1、P2和P3处的峰值压力。其中P1、P2点压力随时间变化曲线与实验数据一致。受溃坝波和自由表面破碎的影响，对P3、P4点数值模拟获得的最大压力略小于实验值。表1展示了不同网格尺度下各测点的最大压力误差，在5 mm网格尺寸下，最大压强误差在P3点，两者误差不超过18%；在8 mm网格尺寸下，最大压力误差在P1点，两者误差不超过15%；而在10 mm网格尺寸下，最大压力误差同样在P1点，两者误差不超过25%。同时数值模拟的压强峰值比实验的压力峰值略微滞后，其可能与数值模拟糙率与试验模型有差异和实验随机误差相关。通过网格密度分析表明，平均网格尺度为8 mm，可满足计算精度要求，同时可减小计算资源耗费。

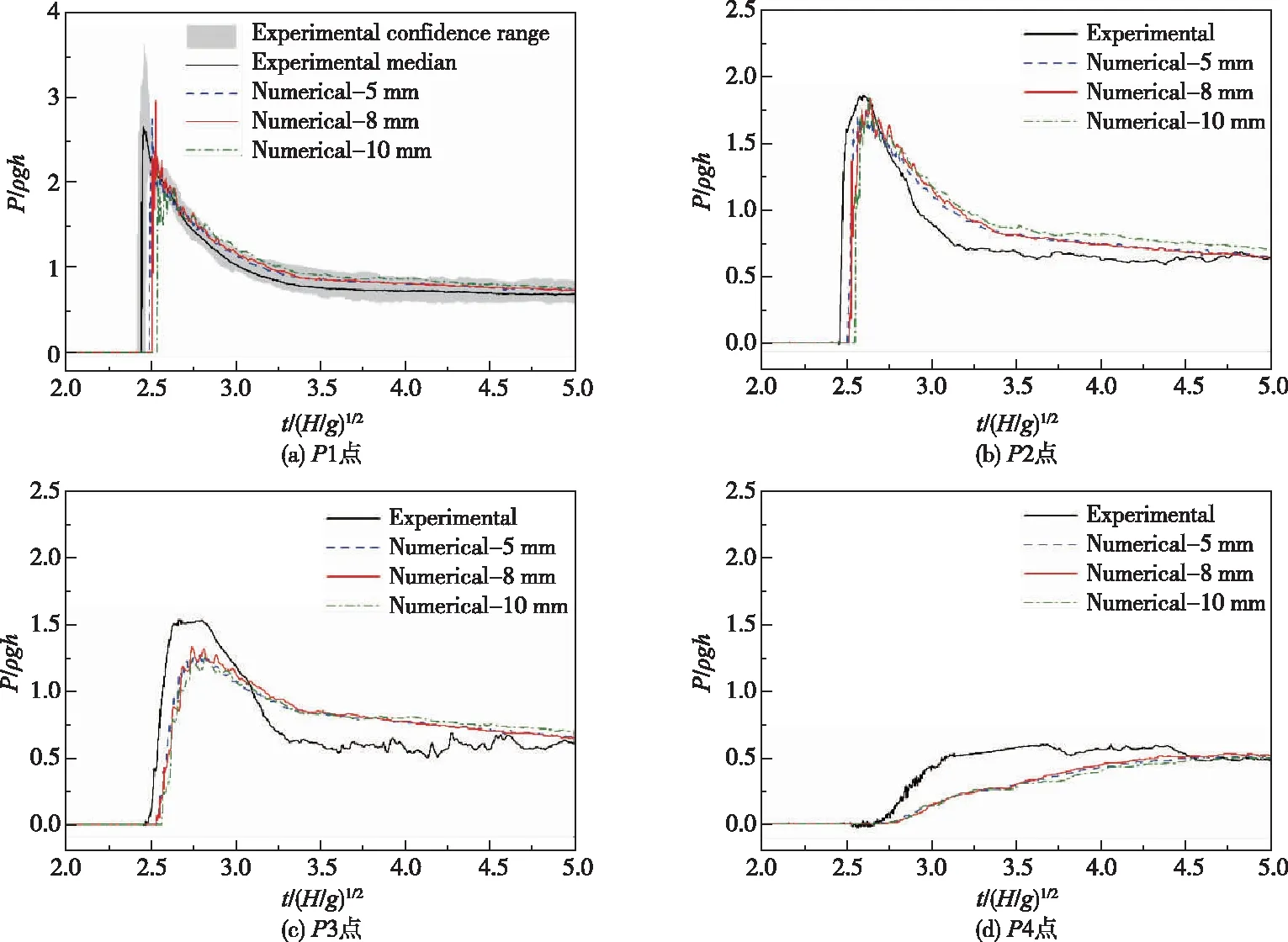
图3 不同网格密度下压力值与实验值对比Fig.3 Comparison of pressure values with experimental values at different grid sizes

表2为水槽H1位置水位在不同时刻下本研究与文献[16]中数值模拟结果与实验结果对比获得的水位相对误差。结果表明本研究与文献[16]相比其相对误差略大，其原因可能是由于本研究采用8 mm的网格尺度略大于文献[16]采用4 mm的网格尺度，同时本研究未涉及闸门的开启过程对溃坝洪水演进的影响。因此在后续模拟研究中将进一步开展网格尺度的研究，并结合考虑闸门开启过程对溃坝水动力过程模拟的影响。

表2 H1位置水位在不同时刻本文与文献[16]的数值模拟结果相对误差对比

2.3 计算模型与数值模拟工况本研究中计算区域及概化示意图如图4(a)所示。计算域为1.61 m×0.15 m×1.5 m立方体，该计算域初始分为两部分，包括闸门上游0.6 m长的水库和下游1.01 m长的湿河床。在下游河床的尾部采用固壁边界用以模拟下游建筑物。计算域其余初始和边界条件与第2节设置相同。水库上游水深为H，下游湿河床水深为h。为了分析这些上下游水深对溃坝水流演进以及冲击压力的影响，在数值模拟中考虑了3个初始上游水深和5个水深比(定义为α=h/H，其中h初始下游水深)，各模拟工况如表3所示。

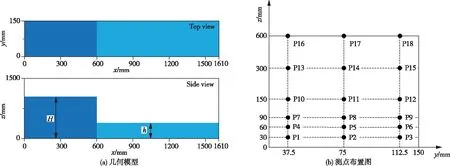
图4 数值模拟的几何模型以及下游墙壁测点布置图Fig.4 Geometric model of numerical simulation and downstream wall measurement point arrangement

表3 数值模拟的初始水深条件

3 结果与分析

3.1 运动学分析本研究主要考虑上下游不同水深对溃坝波演进和下游坝面冲击的影响。选取x1=855 mm、x2=1105 mm、x3=1355 mm、x4=1605 mm断面研究溃坝波的波高演进过程及溃坝波演进的平均速度u。

上游水深H=0.4 m条件下不同水深比对各测点水位变化的影响如图5所示，(a)、(b)、(c)分别为对应下游水深0.04 m、0.12 m、0.2 m，且α分别为0.1、0.3、0.5。

图5 H=0.4 m，α=0.1，0.3，0.5条件下四个测点水位随时间演化规律Fig.5 Evolution rule of water level with time at four measurement points under H=0.4 m，α=0.1，0.3，0.5

当下游水深为0.04 m，对应水深比α=0.1时，各测点水深随时间变化如图5(a)所示，x1位置最大波高为0.157 m，水位峰值到达时间为0.219 s；x2和x3位置处最大波高分别为0.188 m和0.155 m，最大水位峰值对应时间则分别为0.360 s和0.470 s；x4位置最大波高为0.789 m，最大峰值时间为0.839 s。溃坝波导致下游x1至x3区间内水面线峰值呈现一个先增加随后坦化的趋势。而受到下游坝体壁面的影响，x4位置溃坝波接触壁面后发生壅水，波高迅速增加。而对比图5不同水深条件下，α=0.3条件下，其相对峰值(相对峰值为该位置水位峰值减去初始水深)达到最大值。随着水深比增大，其溃坝波传播速度和各点水位峰值均减小。

3.2 冲击动力学分析本研究中设置18个测点用于捕捉下游壁面不同位置压力演化过程，并对不同上游水深和水深比对压力峰值的影响展开分析，测点位置布置如图4(b)所示。

3.2.1 压强变化图6展示了上游水深H=0.8 m，不同上下游水深比α条件下各压力点捕捉到的压强变化过程。在相同α时较低和较高位置的压强随时间变化是明显不同的。根据压强的主要形成原因，较低位置测点的压强可分为两部分：①主要的溃坝洪水波冲击下游垂直坝体墙壁时，由于动能损失而产生的瞬时动压，其大小随冲击速度增加而增加；②洪水波冲击后的静水压强，其大小随垂直坝体墙壁前方水深的增加而增加。

图6 H=0.8，α=0.1、0.3、0.5条件下各压强测量点相对压强演化曲线Fig.6 Relative pressure evolution curves of each pressure measurement point for H=0.8，α=0.1，0.3，0.5

下游水深对洪水波的演进是有阻碍作用且可以缓解洪水波与下游坝体的冲击。当α=0.1时瞬时冲击压强远大于其他任何时间阶段的压强，可达到第一次冲击后最大压强的7.5～22.1倍；α=0.3时瞬时冲击压强是第一次冲击后最大压力的1.1～1.3倍；α=0.5时瞬时冲击压强与第一次冲击后最大压强基本一致。可以得出下游墙壁上部分测点的压强，主要是静水压强，类似于下部分测点的第二种压强。

3.2.2 峰值压强图7(a)、图7(b)是H=0.8 m、α=0.3(h=240 mm)时沿z轴和y轴的峰值压力变化，图7(c)是H=0.8 m、α=0.3～0.5、y=75 mm时沿z轴(垂直方向)的峰值压强变化。

图7 H=0.8 m时各点峰值压力分布Fig.7 Peak pressure distribution at each point at H=0.8 m

当y=37.5 mm或112.5 mm时，峰值变化过程基本重合，如图7(a)所示。受边壁的影响，两侧水流流速小于中间水流流速，导致y=75 mm时峰值压力略大于y=37.5 mm(y=112.5 mm)的峰值压力。但由于整个模拟中计算域宽度仅为15 cm，中间速度与两侧速度也相差较小，所以中间测点峰值压力只是略高于两侧的峰值压强。垂直方向的峰值压强分布呈现先减小再变大再减小的趋势，这是因为下游河床有初始水深，在初始水深之内，沿垂直方向，由于存在静水压强，峰值压强分布是先减小。当超过下游初始水深时，随着z值的变大，峰值压强分布先变大再变小，这是由于冲击压力以及垂直向上的射流引起的。图7(b)展示了压力峰值沿y轴方向呈对称分布，z=0.3 m(P13、P14、P15)、z=0.6 m(P16、P17、P18)是在下游初始水深之上，z=0.3 m的压力值主要是由冲击压强以及静水压强形成，而其余各点的压强值主要是由静水压强值形成。图7(c)则展示了α=0.3～0.5下的压强峰值分布，随着α变大，各点的压强峰值在逐渐变小。峰值压强在垂直方向和水平方向都是呈非线性分布。

图8 α=0.3时不同上游水深在不同水平距离上的沿垂直方向峰值压强分布Fig.8 Distribution of peak pressure along the vertical direction at different upstream water depths at different horizontal distances at α=0.3

图8则展示了在α=0.3时不同上游水深下，峰值压强在不同水平(y轴)距离上的沿垂直方向分布。对H=0.4 m，h=0.12 m分析，z轴方向0.12 m以下位置(线H=0.4 m，h=0.12 m中空心点)的压强主要是由静水压强影响，在0.12 m以上的第一个位置(线H=0.4 m，h=0.12 m中实心点)主要受冲击压强以及静水压强影响，会出现瞬间压强变大，最大峰值压强为12.61 kPa，随后水流受壁面阻挡，发生水位壅高，以上点的压强主要是静水压强形成，是逐渐减小；工况H=0.6 m，h=0.18 m、H=0.8 m，h=0.24 m与工况H=0.4 m，h=0.12 m规律类似，最大冲击压强存在下游初始水深之上第一个点，最大峰值压强分别为22.5 kPa、19.4 kPa。图8(b)和图8(c)与图8(a)有类似的规律，在此就不做赘述。结果表明最大峰值压强主要出现在下游水深之上，由溃坝波引起的冲击压强产生。