追赶法在含闸分洪河道水动力计算中的改进研究
2023-03-14张晓波闪丽洁张瑶兰
张晓波,闪丽洁,张瑶兰
(浙江省水利水电勘测设计院有限责任公司,浙江 杭州 310000)
1 研究背景
河道洪水预报通常采用水文学方法和水力学方法[1],其中水文统计法计算简单,但未考虑洪水在河道内的演进过程[2-3];而水动力学法是严格基于物理机制的水流预测模型,可以较好的模拟河道的水流情况[4-7]。在水动力模型中,描述河道水流运动基本方程组是圣维南方程组[8]。由于是复杂的双曲型非线性偏微分方程组,无法用解析法进行求解,寻求精确、快速的求解方法至关重要[9]。20世纪末,由于计算水力学的兴起,圣维南方程组的数值求解方法得到了迅速发展[10-13]。郑国栋等[14]采用实例对常用且较成熟的Abbott六点中心差分格式、Preissmann隐式差分格式和柯朗格式等数值计算结果进行比较。结果表明Abbott格式计算过程中,震荡较大,收敛较慢,在相同的时间和空间步长下,计算精度较差,且对边界条件类型具有较高的要求;Preissmann隐式差分格式具有相当好的相容性、稳定性与收敛性。基于追赶法的Preissmann隐式差分格式得到广泛应用且可进行快速准确的计算[15-16]。
传统的追赶法适用于无分汊简单河道以及“多个流入河道,一个流出河道”的树状河网[17],虽然计算速度快,但是在处理一些特殊河道(如汊河、环状河道等存在两个以上的流出河道)时,一些断面的追赶系数很难推导,故存在局限性而难以通用,因此需对追赶法的适用性进一步研究。有关河网和汊河的水利计算,以往有不少学者提出处理方法。雷正雄等[17]针对平原河网中较为常见的环状河道和分汊河道提出相应的Preissmann计算格式,用追赶法对各河道进行演算,由水量平衡原理对各节点进行计算。古宇翔[18]建立了适用于叙渝段航道长距离多支流特点的一维非恒定流数学模型,并采用追赶法求解,阐明了支流汇合口处追赶系数的求解方法,突破了多支流条件下非恒定流计算的障碍。朱德军等[19]描述了一个既能模拟树状河网,也能模拟环状河网,而且能处理潮汐流动的数值模型,采用Preissmann格式离散圣维南方程组,并采用Newton-Raphson方法求解非线性离散方程组,汊点处的回水效应采用JPWSPC方法处理。
以往研究多关注分汊的天然河道,较少关注包含闸门调度的分洪河道,而在现实的山区河道中,为保护下游防洪保护对象和城镇的安全,往往会在河道沿程设置分洪闸、泵站等水工建筑物。因此,本文在简要描述传统追赶法的基础上,分析在具有含闸分洪河道的情况下传统追赶法求解的局限性,从而对追赶法进行改进,分别针对河道内分洪闸的不同分洪方式提出了相应的特殊处理方法。同时以东苕溪流域为例,进行实例分析计算,探讨本文所提改进方法的合理性。
2 传统追赶法求解含闸分洪河道水动力问题的缺陷
追赶法的基本思想为:首先根据上边界已知条件计算起始断面的追赶系数,随后依次求出下一个断面直至末断面的追赶系数;与下边界条件联立求得相应的流量和水位,并依次回代求出河道各断面的水位和流量[20-22]。
对于一般的树状河网,以图1为例,是单一河道的有序集合,节点①、②、④、⑤为流量边界,故河道1、2、4和5为已知流量边界的河道;⑦为水位边界,故河道6为已知水位边界的河道;河道3为内河道。因此树状河网水动力计算方法为:每条单一河道均可列出一组对角占优的矩阵方程,已知河道首末边界便可采用追赶法求解;在相邻河道的节点处增列流量平衡和水位相容方程,树状河网水流计算即可转化为单一河道的追赶求解问题。

图1 一般树状河网示意图Fig.1 Schematic diagram of general tree-type river network
对于流量边界条件,各断面的未知量(Z、Q)均有以下追赶方程:
(1)

(2)
式中:Zj、Zj+1分别第j断面和第j+1断面的水位;Qj+1为第j+1断面的流量;Pj+1、Vj+1、Sj+1、Tj+1均为第j+1断面的追赶系数;L1为河网首断面;L2为河网末断面。Y1、Y2、Y3、Y4参数表达详见文献[10]和[18],本文不再赘述。
其中,对于节点③和节点⑥,存在流量平衡和水位相容方程,即入汇点处入流量等于出流量,各断面水位相同。因此对于河道3首断面追赶系数,有以下关系:
(3)
式中:上标代表河道编号;下标为断面位置。
通过方程计算,若节点⑦的水位已知,即可回代求得节点⑥的水位;进而对河道3、4、5进行回代,获得节点③、④、⑤的水位;对河道1、2进行回代,获得节点①、②的水位。如此,整个树状河网的断面水位均可求得,这便是树状河网水流计算的“追赶法”原理。
需要指出,适用以上方法的“树状河网”的前提条件,即对于河道的任何节点,必须满足“一个流出河道”的原则。若存在两个或以上的流出河道,上述“追赶法”则无法求解。以图2为例,树状河网中存在一个以分洪闸控制的分洪河道,节点④上游所有断面的追赶系数均可按上述方法获得,但断面7和13的追赶系数无法获得。这是因为对于节点④,断面7和13所处河道均为流出河道,且基于流量平衡原则,Q6=Q7+Q13。然而由于无法判断Q7与Q13间的分配比例,下游断面的追赶系数无法计算。
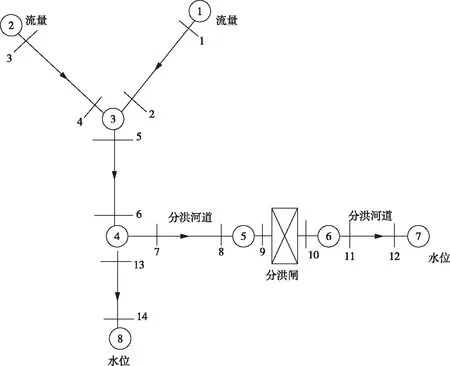
图2 含有分洪河道的树状河网示意图Fig.2 Schematic diagram of tree-type river network with flood diversion channel
另外,对于图2中包含分洪闸的河道,存在Q9=Q10,当分洪闸过流为淹没出流时,闸门过闸流量公式即为闸门前后断面的水位流量关系式,从而可推导出闸前后断面的追赶系数,转化为一般河道求解。而当分洪闸关闸或者自由出流时,过闸流量与闸前后断面水位没有直接关系或者仅与闸前(后)单一断面有关,因此无法建立闸前、后断面间的水位关系,故传统的追赶法无法适用。为解决上述两个重要的问题,本文提出了在含有分洪河道的树状河网水利计算中,追赶计算的特殊处理方法。
3 含闸分洪河道概化的处理方法
为适应传统的树状河网追赶法计算,本文将分洪河道进行特殊处理,如图3所示。基本思想如下:
(1)将分洪河道断面反向编码,将流出河道改为流入河道,形成传统的树状河网结构;
(2)针对分洪闸关闸、开闸自由出流、开闸淹没出流三种状态,分别采取不同的处理方法,详细推导分洪河道的追赶方程。

图3 分洪河道反向编号的河网Fig.3 Schematic diagram of tree-type river network with flood diversion channel reversely numbered
3.1 分洪闸关闸解决思路:以分洪闸将整个分洪河道分割为分洪河道1、分洪河道2及其他河道两个部分分别计算。对于分洪河道1,具有已知条件下边界流量为0,方程组可解;对于分洪河道2及其他河道组成的河网,具有已知条件上边界流量为0,方程组可解。
关闸状态下,首先有Q8=Q9=Q10=Q11=0。对于分洪河道1,首末断面的追赶方程为:
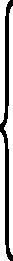
(4)
式中:Z7为上边界水位,作为已知条件;Q8为下边界流量,等于0。因此分洪河道1的各断面未知量均可求得。
对于分洪河道2,首断面11可作为流量边界处理,即Q11=P11-V11Z11=0,故P11=0,V11=0。追赶系数确定后,下游断面的追赶系数即可按照一般河网统一求解。
3.2 分洪闸自由出流解决思路:以分洪闸将整个分洪河道分割为分洪河道1、分洪河道2及其它河道两个河网分别计算。
分洪闸过闸流量为自由出流时,过流公式为:
(5)
式中:ε为侧收缩系数;m为流量系数;b为闸净宽;Zi为闸上水位;Zd为闸底板高程。为适应追赶系数的线性表达方式,对过闸流量公式线性化。假设分洪闸位于第i断面和第i+1断面之间(距离短至可忽略),具体线性化方法见文献[16]。分离位置量Zi如下形式:
(6)

根据实际工程调度,分洪闸自由出流包括两种情况:(1)在洪水前期和中期,主干河道向分滞洪区分洪,即Z10>Z9,过闸流量与Z10有关;(2)在洪水末期,分滞洪区退水至主干河道,即Z9>Z10,过闸流量与Z9有关。该两种情况不仅闸门过流表达方式不同,对分洪河道的计算顺序和方法也有所不同,需分别阐述。
3.2.1 滞洪区退水 分滞洪区退水到主干河道,即Z9>Z10。
将过闸流量公式与分洪河道1的末断面8追赶方程联立,求得过闸流量和末断面水位;同时将此过闸流量作为分洪河道2的已知上边界条件,即可正常求解。
对于分洪河道1的下边界,联立方程如下。由于河道上边界水位已知,故河道下边界的追赶系数P8、V8亦为已知,因此联立过闸流量公式便可求得下边界的Q8、Z8。
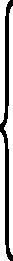
(7)
对于分洪河道2的上边界,联立以下方程,可求得上边界的追赶系数,即P11=V8,V11=0。如此河道下游断面均可按一般河道的追赶法求解。
(8)
3.2.2 主干河道分洪 主干河道向分滞洪区分洪,即Z10>Z9。
虽然分洪河道1下边界的追赶系数P8、V8为已知,但是与滞洪区退水情况不同的是,此时过闸流量与Z9无关,不存在过闸流量公式与之联立求解。因此需换另一种解决思路:将过闸流量公式作为分洪河道2的上边界条件,得到河道首断面的追赶系数P11、V11,便可按一般河道推求下游断面的追赶系数;经过回代后,分洪河道2首断面的Q11、Z11便可求得。继续利用过闸流量平衡原理,即可知分洪河道1的下边界流量,从而求得分洪河道1的各断面水位和流量。需注意的是,过闸流量与断面编号顺序相反,说明分洪的流向。
对于分洪河道2的首断面追赶方程可由以下方程求得P11、V11。之后便可按式(2)继续推求之后断面的追赶系数,并采用式(1)追赶方程回代求得Q11、Q10。
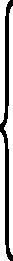
(9)
对于分洪河道1,则由下式取得边界条件,按水位边界条件进行回代计算。
(10)
3.3 分洪闸淹没出流解决思路:无需分割成两个河网。利用过闸流量与闸前、后断面水位的关系,以及水位边界类型的转换,推导出闸前、后断面的追赶系数。
分洪闸过闸流量为淹没出流时,过流公式为:
(11)
式中:μ为综合流量系数,一般情况下μ=2.598 m;b为闸净宽;Zi为闸上水位,Zd为闸底板高程。同理,为适应追赶系数的线性表达方式,对过闸流量公式线性化,方法见文献[16]。
3.3.1 闸前断面追赶系数 对于分洪河道1,由于是水位边界条件,末断面的追赶方程为:
Z8=P8-V8Q8
(12)
对于分洪闸所在河道的首断面追赶系数P9、V9,根据水量平衡和水位相容原理可由下式求得。
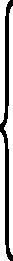
(13)
3.3.2 闸后断面追赶系数 淹没出流也有两种情况:主干河道向分滞洪区分洪,即Z10>Z9;分滞洪区退水到主干河道,即Z9>Z10,相应有不同的表达方式:
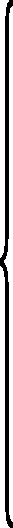
(14)
式中P9、V9为首断面已知的追赶系数,未知追赶系数为P10、V10、S10、T10,可推导得出。
4 应用实例
4.1 流域概况和基础资料苕溪水系属太湖流域,为浙江省八大水系之一。东苕溪是苕溪水系两源之一,主流长151.4 km,平均比降5.1‰[23],发源于天目山脉,经溪口、桥东村、临安,注入青山水库;余杭镇以下河道称为东苕溪,至何家陡门有中苕溪汇入,至瓶窑有北苕溪汇入,至德清城关镇接导流港。流域现状防洪格局为“上蓄、中滞、下泄”[24-25]。“上蓄”即上游建有里畈、青山、水涛庄、四岭、对河口、老虎潭6座大中型水库,防洪总库容2.4亿m3。“中滞”即中游布置蓄滞洪区,其中南湖、北湖滞洪区建有分洪闸,可控制洪水蓄泄,为正常滞洪区;七里、永建、潘板、张堰、澄清滞洪区需采取破堤方式分洪,为非常滞洪区。“下泄”即右岸建有西险大塘和导流东大堤,右岸自上而下建有5座分洪闸,控制导流入湖及东泄分洪。流域概况如图4所示。

图4 研究区域概况图Fig.4 Location of the Dongtiaoxi Basin
苕溪流域降水丰富但时空分布不均匀,汛期雨量约占全年的75%,是浙江省暴雨中心之一[26]。流域地形复杂,干流中上游及支流均为山溪性河流,坡陡流急,水位暴涨暴落;中下游及尾闾河道坡降平缓,洪水短时间难以排出,极易引发倒堤破圩,淹没大片农田和房屋,洪涝灾害频繁[27-29]。历史上流域遭受较严重洪灾有1954年梅雨洪水、1984年梅雨洪水、1996年“6·30”洪水、2013年“菲特”洪水、2019年梅雨洪水等。考虑到流域下垫面一致性和洪水资料获取难易程度,本文选取率定样本为2013年10月6日—9日、2019年7月12日—15日共2场洪水,检验样本为2020年7月4日—7日洪水,包括3场洪水对应的流域内雨量站降雨资料、水库下泄流量资料、特征断面水位资料等。
4.2 模型概化参考传统一维非恒定流模型的建模思路,首先对整个东苕溪流域河道现状水力条件进行分析,结合水文站和雨量站分布划分为子流域,建立产汇流模型模拟各子流域的降雨径流过程,作为水动力模型的输入边界,并在此基础上构建山区河网洪水计算模型。
4.2.1 水文分区产汇流模型构建 依据河流水系、分水岭及下垫面情况等要素,东苕溪流域可细化为26个山区分区和20个平原分区。采用泰森多边形法由流域内雨量站点的雨量加权计算得到各分区的面雨量,再分别对山区和平原分区采用不同的模型计算产汇流过程[30]。
山区分区产流计算采用蓄满产流模型,根据分区集水面积大小选用不同的计算方法。集水面积大于50 km2的分区产流计算采用瞬时单位线法[31-32],小于50 km2的分区产流计算采用“浙江省推理公式法”[33-34]。推算平原分区的产水过程需按照按不同地类进行:水面产水量按照水量平衡方程由降雨扣除水面蒸发推求;水田产水量由降雨扣除水稻蒸腾及水田下渗并考虑水田最大持水深度推求;旱地产水量需根据前期土壤含水量由降雨扣除一定的损失及下渗,并考虑旱地最大持水深度推求;其它地类的产水量则采用径流系数法由降雨推求。
4.2.2 基于改进追赶法的一维非恒定流模型构建 根据流域内水系和水利工程空间分布情况,对东苕溪流域进行模型概化,主要情况如表1所示。模型共概化90个节点、89个河道以及339个断面。已知流量边界条件5个,分别为青山、水涛庄、四岭、对河口、老虎潭水库下泄流量;已知水位边界条件7个,包括流域下游杭长桥水位边界和6个闸下水位边界。流域内的导流五闸、湖州船闸、南湖滞洪区、北湖滞洪区以及5个非常滞洪区均有分洪作用,属于分洪河道,传统的树状河网水流“追赶法”无法解决此类情况。因此本文将分洪河道进行特殊处理,概化方式采用前文第2节所描述的反向编号形式,如图5所示。

表1 模型概化信息表

图5 模型概化图Fig.5 Model generalization diagram of the Dongtiaoxi Basin
模型采用的河道断面数据由2018年实测断面资料整理得到,模型率定时选取河道综合糙率0.025~0.038,基本符合山区性河道糙率系数取值规律。模型计算步长取120 s。
为了更准确分析模型精度,模型中分洪闸调度原则与实际洪水过程中所采用的调度手段一致。具体见表2所示。

表2 模型所采用分洪闸调度原则
4.3 结果分析选取余杭站、瓶窑站和德清大闸为特征断面,对比三个场次洪水的实测与模拟过程,如图6和表3所示。可以看出,在率定期,3个特征断面水位的模拟值与实测值演变趋势相同,且对水位峰值出现时间和峰值大小模拟效果较好,确定性系数均大于0.81,其中2013年模拟效果最好;但对退水段模拟有待改进,尤其是2019年,退水段水位偏高。检验期除余杭断面水位预报确定性系数均小于0.80之外,瓶窑和德清大闸断面确定性系数大于0.80,满足《水文情报预报规范》(GB/T 22482—2008)中规定的乙级预报精度标准,可用于作业预报。
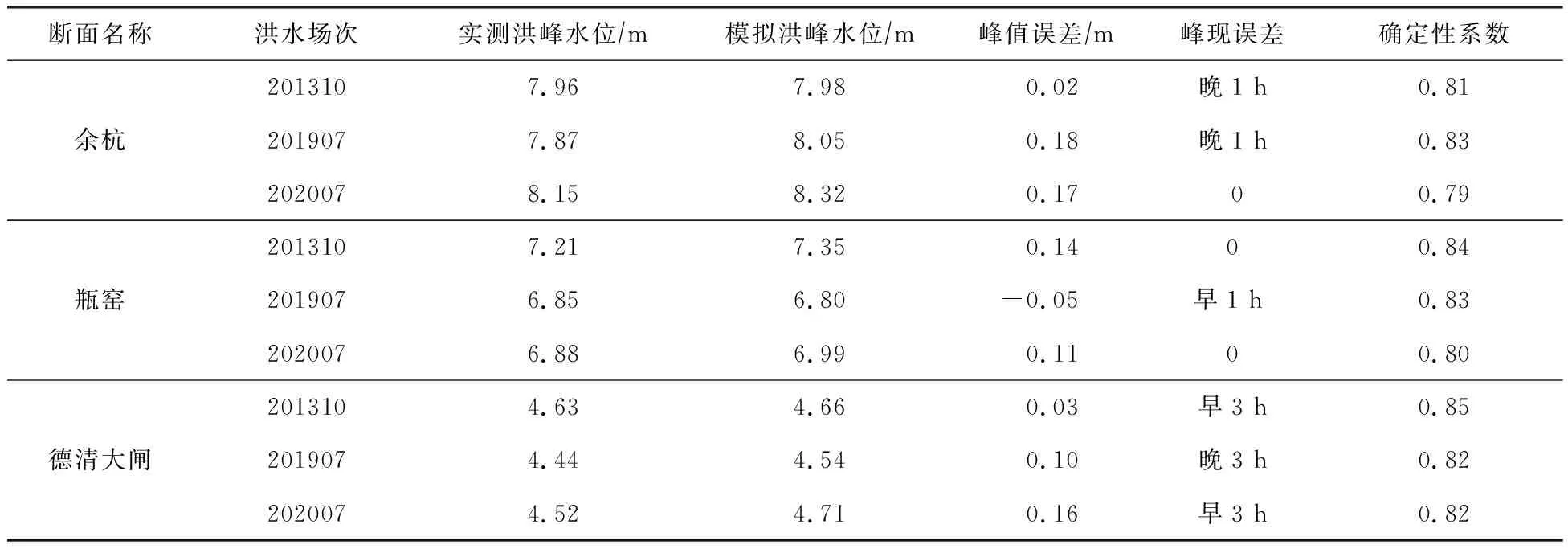
表3 模型洪水位计算结果

图6 东苕溪流域特征断面洪水位实测与模拟对比图Fig.6 Flood level predictions of characteristic sections in the Dongtiaoxi Basin
本文选取的3场历史洪水中,根据瓶窑洪水位上涨情况,均对北湖分洪闸进行开闸分洪,北湖滞洪区发挥了较大的滞洪作用。表4统计了3场历史洪水北湖滞洪区分洪情况。可以看出,将实际开闸时的瓶窑水位作为模型中北湖滞洪区的开闸条件,模型所判断的开闸时间与实际开闸时间接近,间隔均在0.5 h之内;模拟分洪水量比实际偏大,但相对误差均控制在10%以下。

表4 北湖滞洪区分洪情况对比
另外,为了便于对比,本文同时搭建了丹麦DHI公司的MIKE11模型,所采用的基础数据保持一致。在计算效率方面,若采用计算时间步长为120 s,采用MIKE11模型模拟东苕溪流域72 h洪水过程耗时12 min;而基于改进追赶法计算时长仅需45 s,计算效率大大提高。在稳定性方面,由于东苕溪上游为山区河道,坡度较大,加之洪水初期河道中为基流,使用MIKE11模型计算时出现露底情况,导致计算崩溃,采用人工挖深槽的方式加以解决,但是计算洪水过程震荡较大,收敛较慢;而改进追赶法过程线拟合较好,不存在明显的震荡过程。在精度方面,由于MIKE11模型计算过程中震荡较大,收敛较慢,故计算精度相对较差。综合来讲,本文所提出的“追赶”计算特殊处理方法计算效率相比MIKE11模型大大提高,同时模型稳定性强。
5 结论与展望
针对传统的追赶法无法解决含有分洪闸、分洪河道的树状河网水利计算问题,本文根据分洪闸不同出流情况,对传统追赶法进行改进。以东苕溪流域为实例,分析计算方法的合理性和准确性。得到以下结论:
(1)将分洪河道断面反向编码,将流出河道改为流入河道,此时分洪河道上边界条件为已知水位,即可形成一般的“多个流入河道、一个流出河道”的树状河网结构,可采用传统的追赶法思路求解。
(2)针对分洪闸关闸、开闸自由出流和开闸淹没出流三种情况,分别讨论与之对应的模型概化方法,通过对分洪河道采取反向编号、河网分割、边界类型转换衔接等方法进行特殊处理,实现采用追赶法的思路求解。
(3)在东苕溪流域上进行实例计算,分别将模拟结果与实测洪水和MIKE11模型计算成果做对比分析得知,本文所提出的“追赶”计算特殊处理方法合理,拥有计算效率高、模型稳定性强等优势,适应山区河道坡度大的特性,可有效解决含有分洪河道的树状河网水利计算问题。
另外,在山区型河流中,水流的流态往往很复杂,受分洪闸启闭的影响,常伴随着临界流、急流等流态,甚至会出现水流间断的现象[35],此类现象在计算方法改进时需全面考虑。因此,考虑到确保山区河道追赶法计算的稳定性,日后需要对计算方法做进一步改进优化,以适应分洪河道计算的需要。
