基于长短时神经网络的卫星陀螺仪故障检测*
2023-03-13林珏琪
徐 驰 林珏琪
中山大学物理与天文学院,珠海 519082
0 引言
卫星长期在复杂的空间环境中工作,星上设备常有故障发生。陀螺仪为姿态控制系统提供卫星姿态信息,它正常稳定运行对卫星姿态控制具有举足轻重的影响[1]。因此,及时准确检测陀螺仪故障并采取有效措施能够提高卫星可靠性,保证航天任务顺利进行。
陀螺仪的故障检测方法主要有3类[2]:1)基于模型的方法[3-4]、基于信号处理的方法[5]以及神经网络的方法[6-7]。目前,基于模型的方法需要依赖由陀螺仪和星敏感器构成的冗余配置,并且建立的模型与系统真实运行情况间存在误差。而基于信号处理的方法过于依赖信号特征的变化,存在故障漏报的风险。神经网络具有强大的非线性逼近能力,高效的处理能力以及良好的自适应性,成为卫星陀螺仪故障检测的重要手段。目前在卫星陀螺仪故障检测方面采用的大多数是一些结构简单的神经网络,这将导致模型拟合能力较弱,泛化性能较差,从而影响卫星陀螺仪故障检测能力。相比于传统神经网络,LSTM神经网络更适于时间序列的处理,能够快速、准确地实现陀螺仪故障检测。
本文提出了一种基于LSTM神经网络的卫星陀螺仪故障检测方法。首先,利用陀螺仪正常数据训练LSTM神经网络得到陀螺仪正常工作输出模型。然后,通过网络产生的预测误差进一步得到检测阈值。最后,利用完成训练的输出模型实现在线检测,根据检测误差是否超出阈值判断故障是否发生。利用半物理仿真平台模拟的数据,验证提出算法的准确性和有效性。
1 模型分析
1.1 卫星姿态系统模型
卫星姿态控制系统,具体由卫星本体、姿态敏感器(星敏感器和陀螺仪)、姿态控制器和执行器构成。其中,姿态敏感器测量出卫星姿态信息,姿态确定算法得出卫星的估计姿态,控制器根据估计姿态与期望姿态,依照控制律输出控制命令,执行机构根据指令输出控制力矩,完成卫星姿态控制。
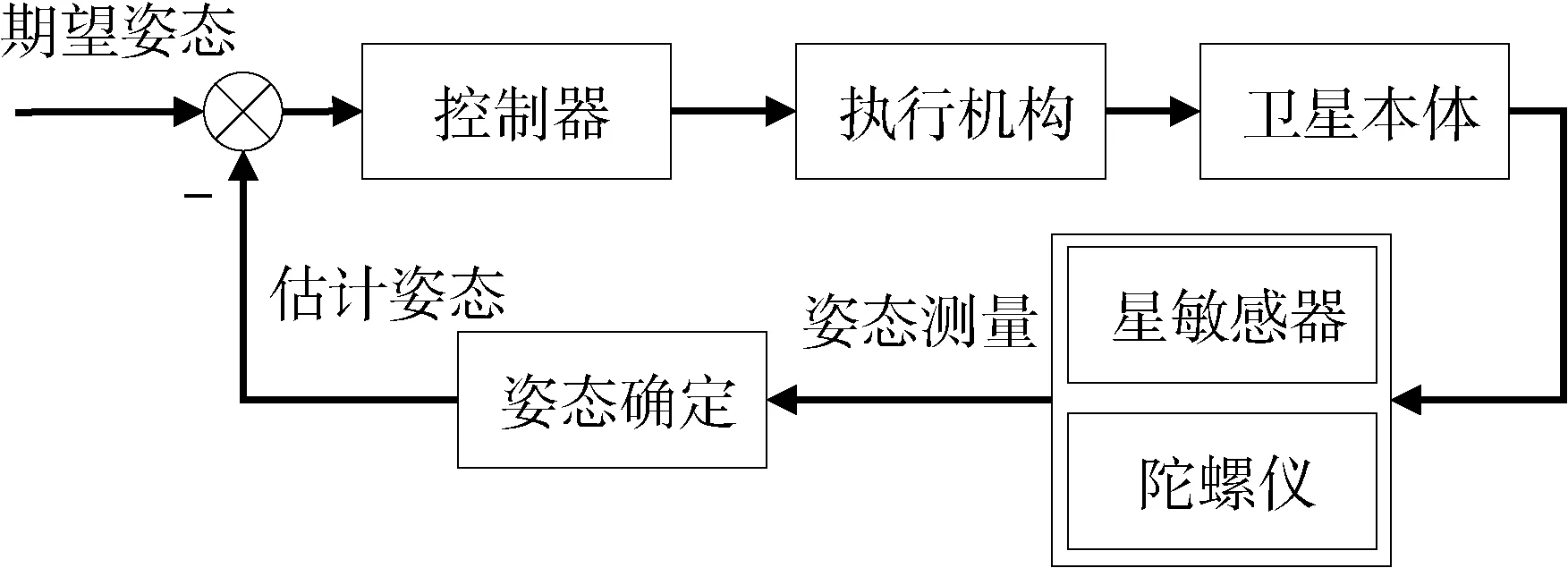
图1 卫星姿态控制系统原理图
由四元数定义的卫星姿态运动学方程为:
(1)
式中:q=[q1,q2,q3,q4]T为卫星姿态四元数,ω=[ωx,ωy,ωz]T为卫星相对参考坐标系的转动角速度,其中:
利用欧拉方程描述卫星的动力学方程:
(2)
式中:H=Iω为卫星转动角动量,H×表示为H的反对称矩阵;I表示卫星的转动惯量矩阵;Td表示为外部干扰力,Mc表示为姿态控制力矩。
1.2 陀螺仪数学模型与故障建模
在卫星姿态控制系统中,陀螺仪测量惯性系下的卫星角速度在测量系下的投影,由于陀螺仪通常安装在卫星本体坐标系下,此时测量系与卫星本体坐标系重合,陀螺仪数学模型[8]表示为:
(3)
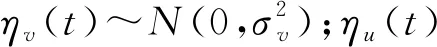
陀螺仪的常见故障有卡死故障、噪声故障、偏差故障3种形式[8]。
1)卡死故障:由于表头故障,陀螺仪输出为一定值,实际输出为:
(4)
式中:ωo(t)为陀螺仪的实际输出;ωe(t)为陀螺仪的理论输出;tf为故障发生时刻。
2)噪声故障:由于线路盒电压输出不稳,陀螺仪测量时随机噪声突然增大,实际输出为:
(5)
式中:ωf(t)为陀螺仪测量噪声,n噪声为故障增益,通常随机噪声增益扩大到2倍以上(即n>2),认定为噪声故障。
3)偏差故障:由于漂移增大,导致陀螺仪输出出现偏差,实际输出为:
(6)
式中:Δω(t)为故障偏差信号。
2 基于LSTM神经网络的陀螺仪故障检测方法
2.1 LSTM网络
LSTM神经网络是一种用于处理时间序列的循环网络(RNN, Recurrent Neural Network),其通过独特的门限机制,控制前期信息的积累速度,可以解决RNN网络梯度爆炸和长期依赖问题[9-10],具体结构如图2所示。LSTM网络结构中的遗忘门、输入门和输出门用来控制细胞状态。
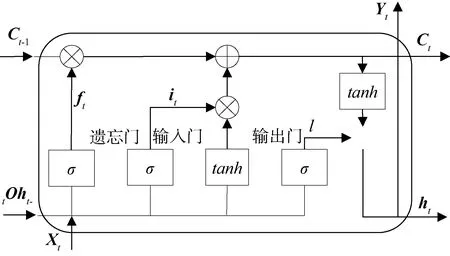
图2 LSTM网络单元结构
LSTM网络单元结构中信息流动可以用式(7)~(11)来表示:
ft=σ(Wf·[ht-1,Xt]+bf)
(7)
(8)
(9)
Ot=σ(Wo·[ht-1,Xt]+bo)
(10)
ht=Yt=Ot⊗tanh(Ct)
(11)
式(7)~(11)中:⊗表示两个向量元素对应相乘;σ(·)为Sigmoid函数;tanh(·)为Tanh函数;变量Wζ与bξ,其中ζ,ξ∈(f,i,c,o)分别表示在不同位置的输出权重和偏执矩阵。
2.2 故障检测流程
本文提出一种基于LSTM神经网络的陀螺仪故障检测模型,具体框架如图3所示。
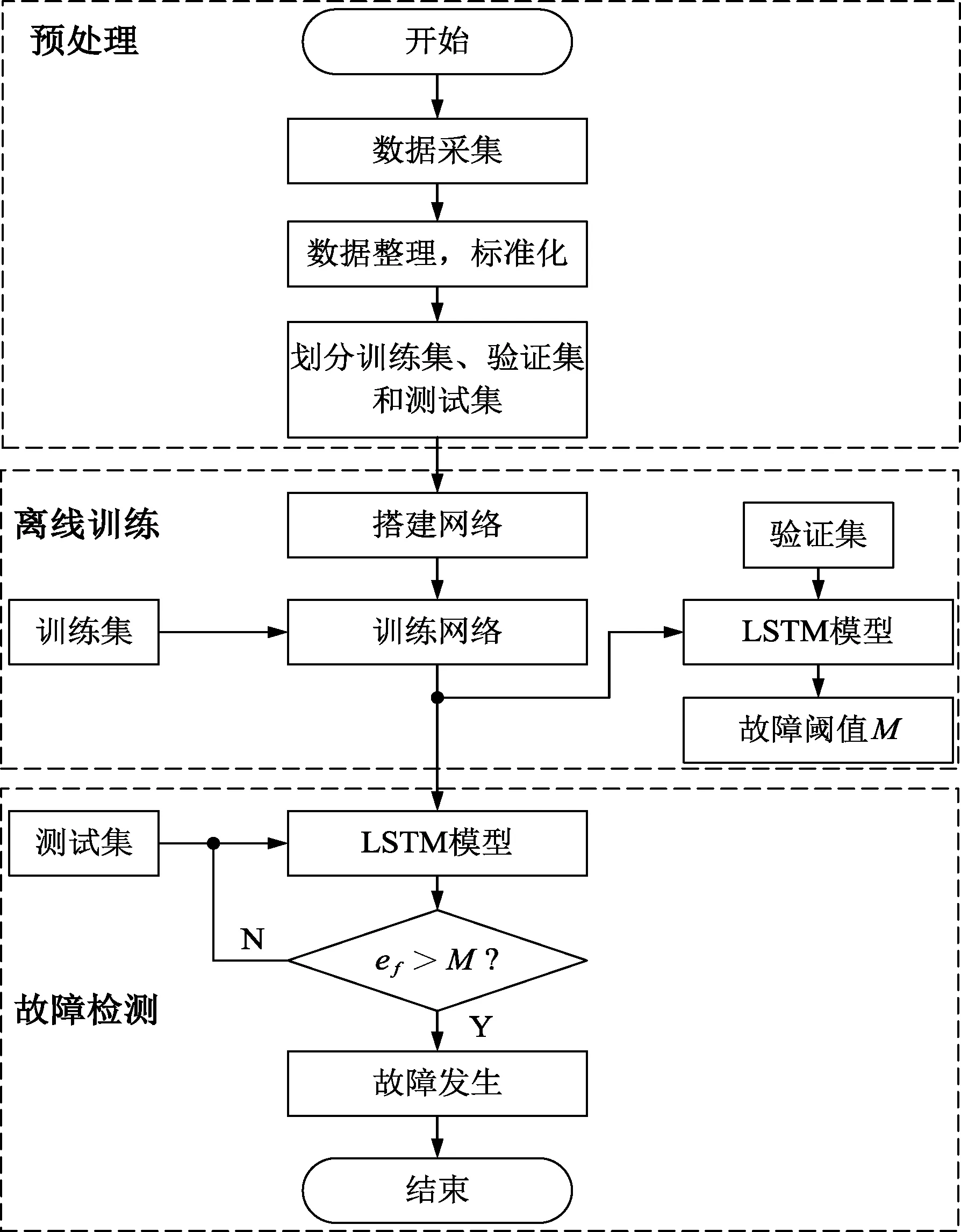
图3 基于LSTM的卫星陀螺仪故障检测流程框图
1)预处理阶段
采集频率10Hz记录实验数据,整理陀螺仪正常卡死故障、噪声故障以及偏差故障数据,完成数据归一化,本文采用归一化方法如式(12)所示:
(12)
式中:ω,ωmin和ωmax分别表示原始数据以及数据中最小值与最大值,ωm表示归一化后数据值。
将归一化后的数据进一步划分用于网络训练的训练集Vt,设定故障阈值的验证集Vd,以及测试模型实时性与准确性的测试集Vf。
2)离线训练阶段
将训练集Vt按照输入时间长度ls划分,得到一组时间序列,且依次后移一个输入时间长度,以此形成输入LSTM网络训练的数据集。然后,将训练输入LSTM网络的输入层,经过多层LSTM网络的隐藏层处理后,进一步导入全连接层,保证此时的数据维度降低至与标签一致,即输出时间长度lp,对应关系如式(13)所示:
(13)
式中:LSTM(·)表示LSTM神经网络处理数据过程。最后,利用反向传播算法(Back-Propagation Through Time, BPTT)计算网络模型结构参数,得到训练完成的LSTM模型。
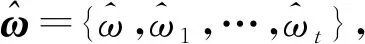
(14)
本文通过计算无故障时预测误差数值的平均值与标准差获得阈值的表达式:
M=ηe+α×δe
(15)
式中:μe和δe残差eTr的均值和标准差,α为常数,当α=2.6时,此时达到99%的置信区间[11]。
验证集Vd中陀螺仪输出角速度数据输入训练好LSTM网络,网络输出预测值,根据式(14)得到预测误差ev,根据式(15)得到故障阈值M。
3)检测阶段
测试集Vf含故障数据集中的角速度数据输入训练完成的LSTM网络,网络输出预测值,通过预测误差ef与故障阈值M的比较,判定故障是否发生。
3 仿真校验
仿真试验包括故障数据采集、网络训练以及故障检测3个部分。
3.1 数据采集
设定仿真实验步长为0.1s,陀螺仪常值漂移取β(t)=1((°)/h)、零均值高斯噪声方差取σv=0.1((°)°/h)和漂移均方差取σu=0.01((°)/h)。设定星敏感器传递系数为0.99,输出卫星姿态信息,并且陀螺仪与星敏感器测量坐标系与卫星本体坐标系重合。卫星转动惯量矩阵
首先,利用Matlab2020a完成卫星姿态控制系统的搭建,并且记录正常情况下陀螺仪的输出数据。其次,根据式(3) ~ (5)中陀螺仪故障模型,将各个故障状态时陀螺仪输出特征注入正常情况的系统,得到各种故障状态下陀螺仪输出数据,故障注入的时间是随机,并且持续一段时间。最后,正常、卡死故障、噪声故障、偏差故障下陀螺仪输出数据每种分别采集2000组。正常数据分成训练集Vt、验证集Vd,其中,训练集Vt用来训练LSTM网络预测模型,不断优化网络结构参数;验证集Vd用来输入训练完成的LSTM网络模型,利用预测误差ev,不断调整灵敏度常数,计算故障检测阈值。由卡死故障、噪声故障和偏差故障数据构成的测试集Vf用来验证基于LSTM神经网络的陀螺仪故障检测模型的准确性。
3.2 网络训练与对比
正常训练集Vt数据建立LSTM网络预测模型,采用梯度下降法进行训练,根据经验与实验测试设定网络模型参数。本文选定LSTM网络的输入时间窗口长度为ls=300,输出时间窗口为lp=1。LSTM神经网络总设定有3个隐藏层,每层分别含有64,256,100个神经元,每层之间设置0.2的丢弃率,防止模型过拟合。设置网络学习率为0.005,训练循环迭代训练250次。将验证集Vd中一组数据代入训练好的LSTM网络,真实值与网络预测值对比如图4所示,LSTM网络预测值可以很好地随着真实值波动,无突变。
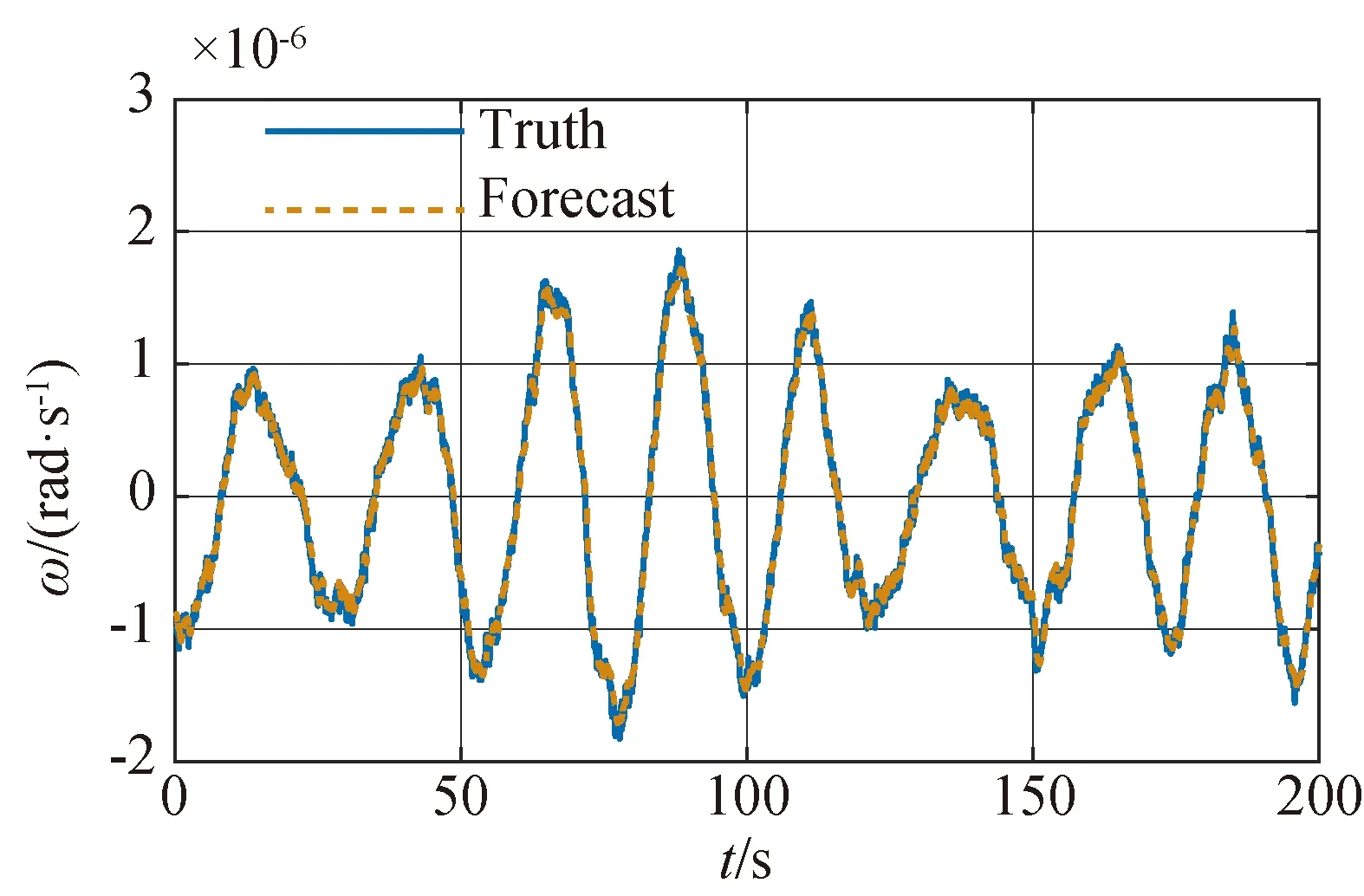
图4 真实值与LSTM网络预测值
模型预测值与真实值越相近,预测误差波动范围越小,模型对故障导致输出的变化越敏感,故障检测越准确。为了反映训练完成网络模型预测值与真实值之间误差差距,以误差均方根差(root mean square error, RMSE)的大小进行衡量,则其公式如下:
(16)
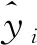
同时,为验证LSTM网络对陀螺仪输出数据学习预测性能优异,利用训练集Vt对参数相同的ANN(Artificial Neural Network)、FNN(Feedforward Neural Network)、RNN以及LSTM网络进行训练,并且选取10组验证集中数据进行测试,取每组预测误差RMSE的平均值进行比较,结果如图5所示。
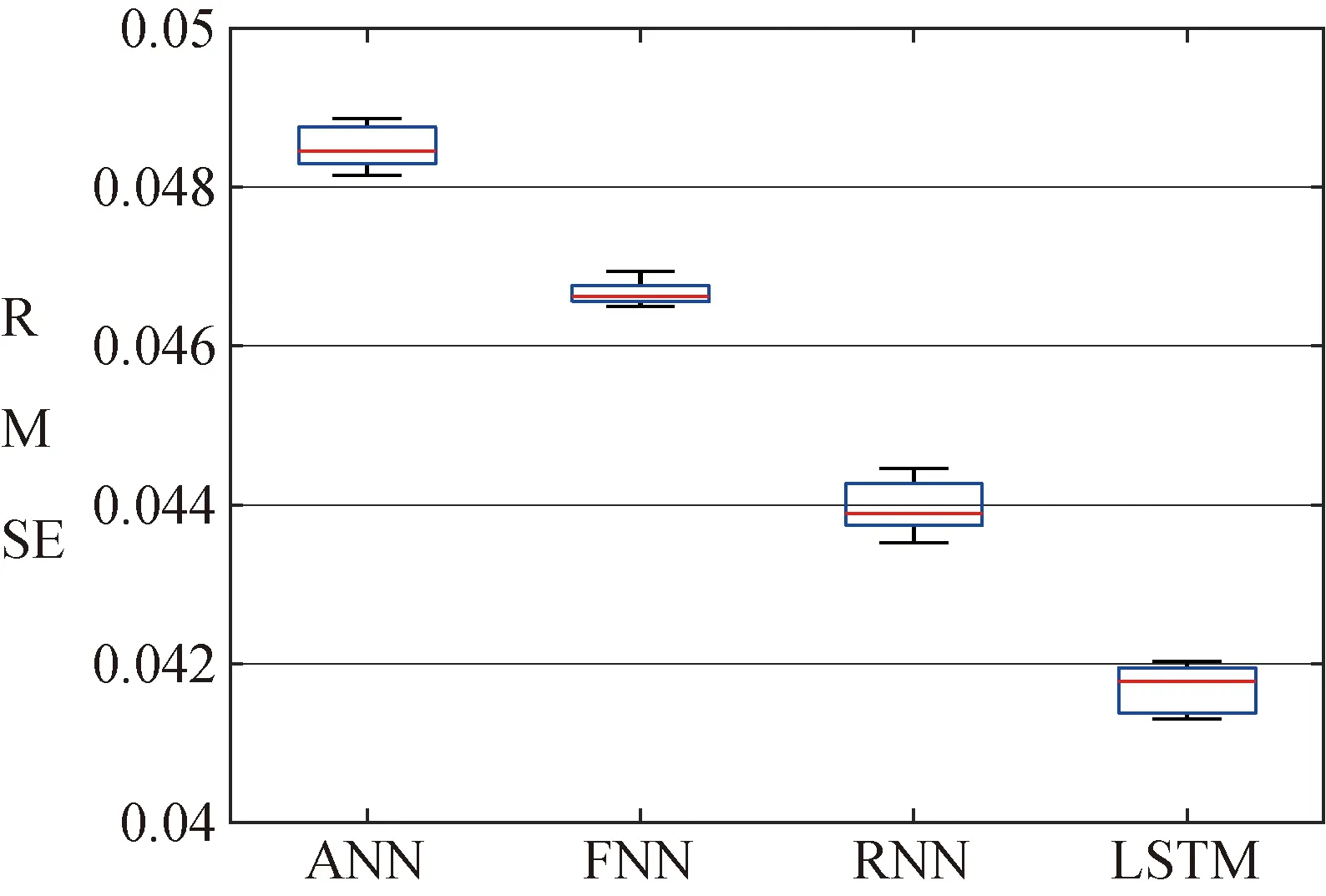
图5 四种神经网络预测残差的RMSE比较图
LSTM网络模型预测误差RMSE分布中位数为rmseLSTM=0.0418,均低于其余网络(rmseANN=0.0483,rmseFNN=0.0465,rmseRNN=0.0438)。由于ANN和FNN网络结构无法对过往信息进行利用,RNN网络缺少门控结构,无法对过往信息进行取舍利用,故LSTM网络预测模型的表现优于ANN,FNN和RNN网络。
3.3 故障阈值计算
验证集Vd数据输入完成训练的LSTM神经网络,通过网络预测值与真实值的比较,得到预测误差的分布,取阈值灵敏度常数α=2.6,如图6所示。
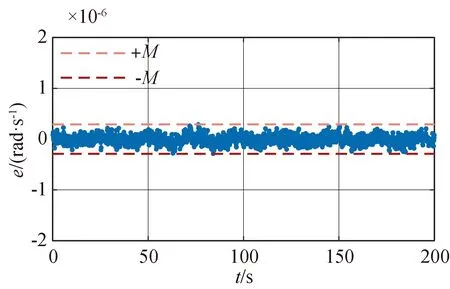
图6 当α=2.6时预测误差与故障阈值
3.4 故障检测
在陀螺输出无故障、卡死故障、噪声故障以及偏差故障情况下,模型预测值与真实值对比以及预测误差结果如图7~9所示。
1)卡死故障发生时,陀螺仪输出角速度数据不再发生变化,与前一刻相同,如图7(a)所示,0~30s输出正常,30~50s卡死故障发生,输出不再变化。基于LSTM网络模型的预测值未受到卡死故障的影响,故障发生后,预测值正常波动,且其与真实值之间出现偏离,导致预测误差逐渐靠近故障阈值,于1.2s后超出,判定故障发生,如图7(b)所示。由于无故障下,陀螺仪输出近似于正弦波动,故障发生时刻会影响到预测误差超出阈值所用的时间,即检测时间,通过多组实验,检测时间在0.8~2.0s范围内;
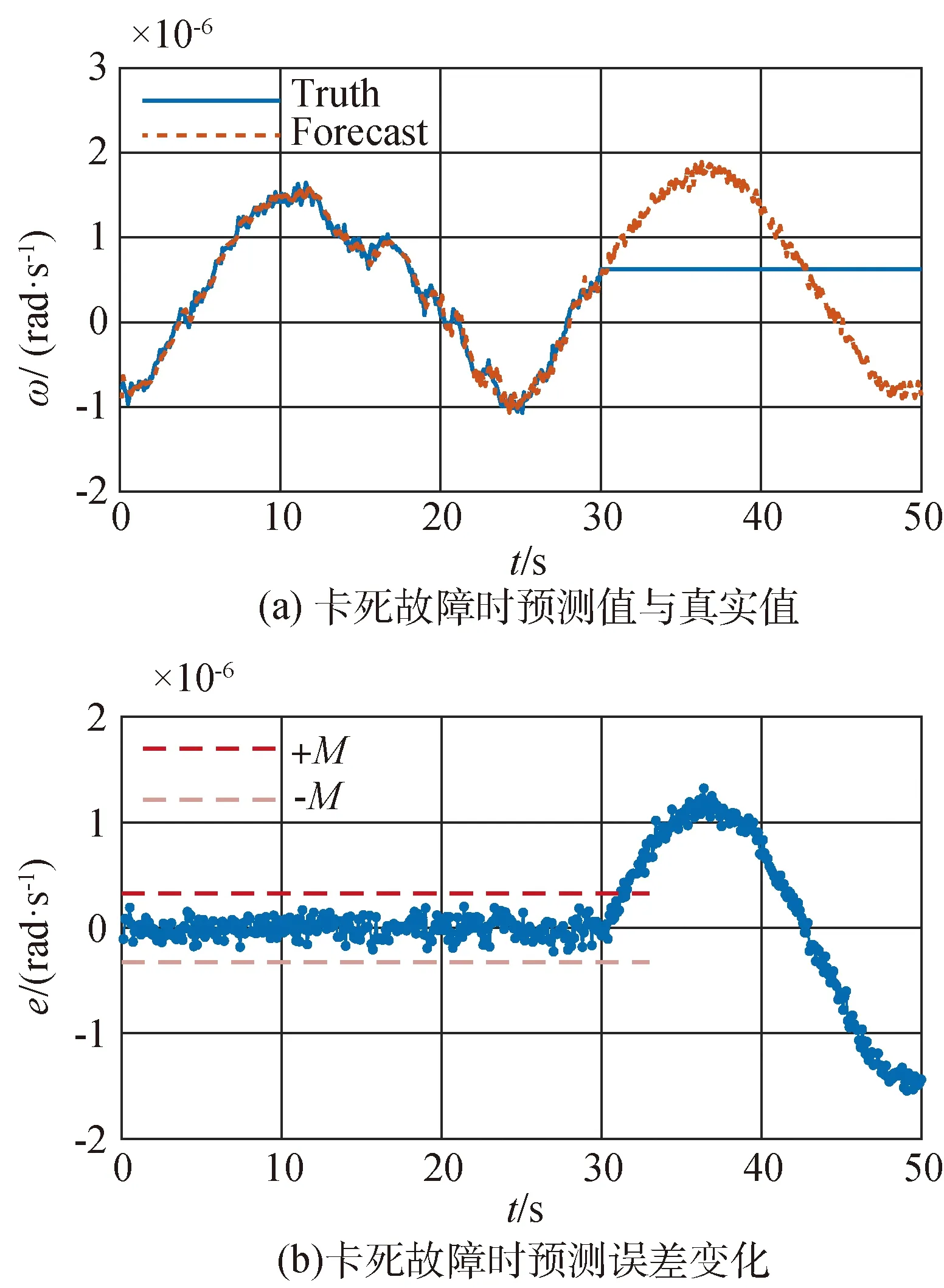
图7 陀螺仪发生卡死故障
2)噪声故障发生时,陀螺仪输出角速度数据噪声增大,如图8(a)所示,0~30s输出正常,噪声故障于30~50s间发生,此时噪声故障增益系数取n=3。虽然基于LSTM网络模型的预测值与真实值的趋势走向相同,但是由于噪声故障发生,预测误差波动范围发生变化,预测误差便迅速超出故障阈值,判定故障发生,如图8(b)所示;
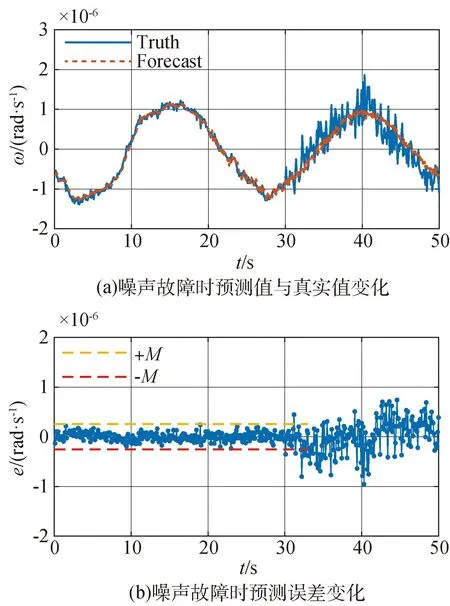
图8 陀螺仪发生噪声故障
3)偏差故障发生时,陀螺仪输出角速度数据有较大的突变,如图9(a)所示,0~30s输出正常,30~50s偏差故障发生,此时故障信号取Δω=1.5×10-6rad/s。故障发生后,模型预测值未受到偏差突变的影响,预测值正常波动,而由于偏差的存在,预测误差迅速超出故障阈值,判定故障发生,如图9(b)所示。
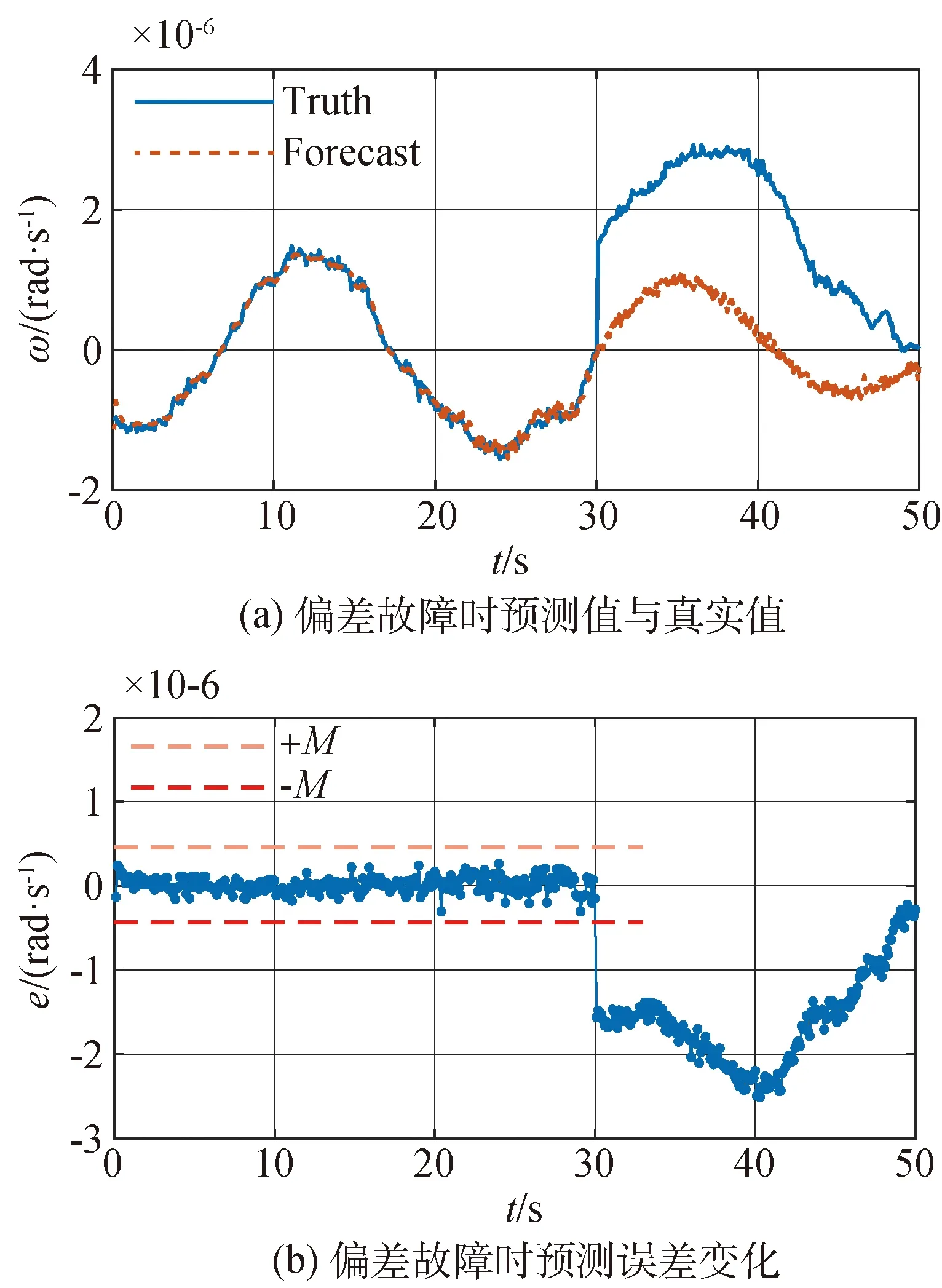
图9 陀螺仪发生偏差故障
综上,基于LSTM神经网络的陀螺仪故障检测模型,针对陀螺仪卡死故障、噪声故障以及偏差故障均能完成故障检测。同时,分别对3种故障数据进行多组测试,统计模型的准确率,结果如表1所示。针对陀螺仪的3种故障类型都能完成检测,该方法在总体实验样本达到98.9%的准确率。
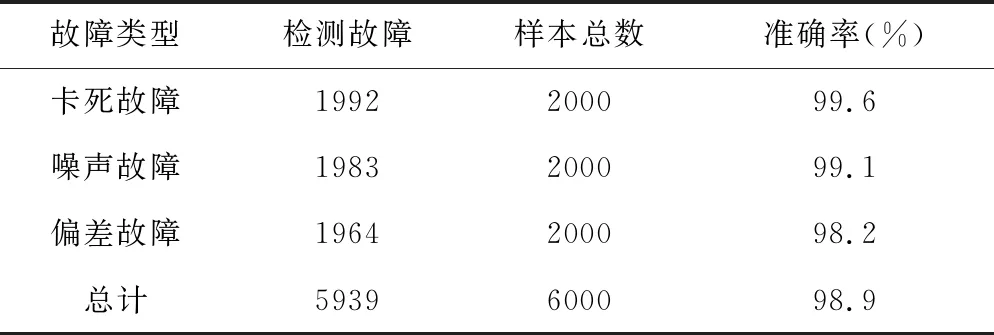
表1 不同故障下模型检测准确率
4 结论
基于LSTM神经网络设计了卫星陀螺仪故障检测方法,包括对LSTM网络的训练、不同网络对比、故障阈值选取以及故障检测等内容。实验结果表明:
1)与相同结构的ANN、FNN以及RNN网络相比,通过对比预测误差的RMSE大小,得出LSTM网络对陀螺仪输出数据学习预测效果更优;
2)选择合适的故障阈值之后,LSTM模型能在2s内检测出陀螺仪卡死故障、噪声故障以及偏差故障,并且总体的准确率达到98.9%。
当前本文完成陀螺仪故障检测,未来将进一步利用不同故障间的预测误差特征实现故障隔离。
