冲积土中封闭填实爆炸自由场应力波传播特性的实验研究

卢 强,丁 洋,李 进,方厚林,陶思昊,唐仕英,刘赟哲

(西北核技术研究所,西安710024)

地介质中应力波传播特性的基本规律是评估爆炸加载后地下结构毁伤效果或地下结构防护能力的重要依据。由于地下爆炸应力波的衰减规律受场地介质和爆炸当量的影响[1],因此,在现场开展地下爆炸实验是获得目标地介质中应力波传播特性最直接的手段,国内外诸多学者也开展了大量的研究。Perret等[2-3]搜集整理了美国大量地下爆炸实验数据,研究了冲积土、干(湿)凝灰岩、盐岩及花岗岩等介质中强爆炸的应力波传播特性,给出了粒子比加速度、速度及比位移等运动参数峰值的传播演化规律。Wheeler等[4]以Perret等搜集整理的数据为基础,进一步分析了不同地下爆炸当量实验的相似性及自由场应力波参数对岩土力学特性的依赖性。Murphy等[5-6]进一步对美国地下强爆炸的自由场应力波数据进行了整理分析,给出了冲积土、凝灰岩、大理岩、盐岩、花岗岩、砂岩-页岩及枕状熔岩等介质中自由场应力波实测数据。Melosh[7]基于冲积土、盐岩、花岗岩、凝灰岩等场地的地下强爆炸实验数据,分析了粒子速度上升时间的变化规律,这对于认识地下爆炸应力波形状的演化规律具有借鉴作用。黄理兴等[8]全面介绍了我国岩石动力学研究的状况,指出地下爆炸应力波在岩土介质中传播与衰减规律对于国防建设和国民经济发展的重要意义。李孝兰[9]针对自由场岩体应力波测量的特点,分析了测量系统的频响要求,提出了自由场应力波探头的布设原则及阻抗匹配问题。王占江等[10-11]对石灰岩中50～2 000 kg TNT和花岗岩中1～150 kg TNT球形装药爆炸实验的自由场应力波传播特性进行了研究,给出了自由场应力、地表粒子速度、地表比位移及地表比加速度等应力波参数的衰减规律,讨论了地下爆炸波传播路径对应力波参数的影响。赵红玲等[12]开展了石灰岩中27 kg TNT装药下不同埋深爆炸实验,对直接地冲击参数传播规律进行了研究,给出了不同埋深爆炸地冲击效应与封闭爆炸直接地冲击等效的计算公式,这对快速评估不同埋深爆炸条件下的地冲击环境有重要价值。卢强等[13-16]研究了基于实测自由场应力波数据反演岩土介质本构、构建地下爆炸应力波流场及获得地下爆炸震源函数的方法。

上述研究中涉及了多种当量、多种场地的地下爆炸应力波的传播特性,实测数据的特点包括：(1)场地介质不同时,自由场应力波的传播特性有很大不同,主要体现在粒子的加速度、速度及位移等应力波参数随传播距离的增加而衰减,但衰减的快慢有较大区别;(2)相同的场地,由于介质的不均匀性,不同爆炸实验获得的应力波参数具有一定的离散性。本文选择某场地冲积土介质为研究对象,设计并开展了10 kg TNT和30 kg TNT球形装药的地下封闭填实爆炸实验,得到该场地自由场应力波特征参数(粒子的加速度、速度、位移及速度上升时间)的传播演化规律,给出了实测应力波特征参数与经验拟合公式的相对偏差,为该场地地下爆炸地冲击载荷强度区间的估计提供依据。同时,结合美国开展的不同当量地下爆炸实验数据,对比分析了粒子速度上升时间与粒子速度峰值及爆炸当量的关系。

1 实验概况

实验场地介质为冲积土。通过现场钻孔取样分析,实验场地约有几十米厚的不含水冲积土层,其中近地表3～5 m范围内为松散的冲洪积土砾石层,深度为数米至几十米范围内为胶结和半胶结状态的冲洪积砾石、砾砂、卵石及粉质黏土等。基于地震波物探方法反演得到实验场地附近的地质速度结构,近地表深度为3～5 m范围内地震波纵波速度约为几百米每秒,深度为数米至几十米范围内地震波纵波速度为1 350～1 500 m·s-1。

本轮共开展3发地下封闭爆炸实验,均为中心起爆的球形装药,其中一发当量为10 kg TNT(代号为S10),其余两发当量为30 kg TNT(代号为S30-1和S30-2),图1为实验现场布局示意图。在地表选定爆心投影点后,利用钻机钻出多个一定深度的孔,用于装药和安装地下测试传感器。为尽量减少对地介质的扰动,所有钻孔的直径均略大于炸药和测试传感器安装装置的直径。在深孔内安装炸药和传感器后,采用回填材料对所有钻孔进行回填,回填材料和地介质的阻抗比约为0.94,可满足地介质中运动量测试要求。测试孔中主要安装了加速度和速度传感器,部分测点同时安装了1～2个加速度计和1个速度计进行复记,所有的传感器均对准爆心安装,测量的均是径向运动量。3发实验参数如表1所列。其中：Q为爆炸当量;H为埋深;r1为最小爆心距;rN为最大爆心距。

实验测量系统由前置传感器、二次仪表、数据记录仪器以及控制系统组成。数据记录仪器的采样频率为100 kHz,前置加速度传感器的频响为0.5 Hz～6 kHz,速度传感器的频响为4 Hz～4 kHz。

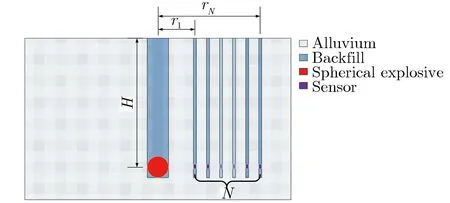
图1 实验现场布局示意图

表1 3发实验参数

2 实验结果

图2、图3分别为S10,S30-1,S30-2实验实测的部分加速度a和速度v随时间t的变化关系。图中r为传感器距爆心的实际距离。所有实测结果除扣除传感器基线零漂外,未对数据做任何处理。由图2和图3可见,实测数据的信噪比较高,除近区的部分传感器有一定的高频毛刺干扰外,其他信号相对光滑;离爆心最近的速度计因量程较小,部分出现限幅现象;在靠近爆心附近的测点处,加速度信号在首个正向脉宽内出现双峰值现象,随着传播距离的增加,首个正向脉宽内的双峰值逐渐变为单峰值。

(a)S10 near field

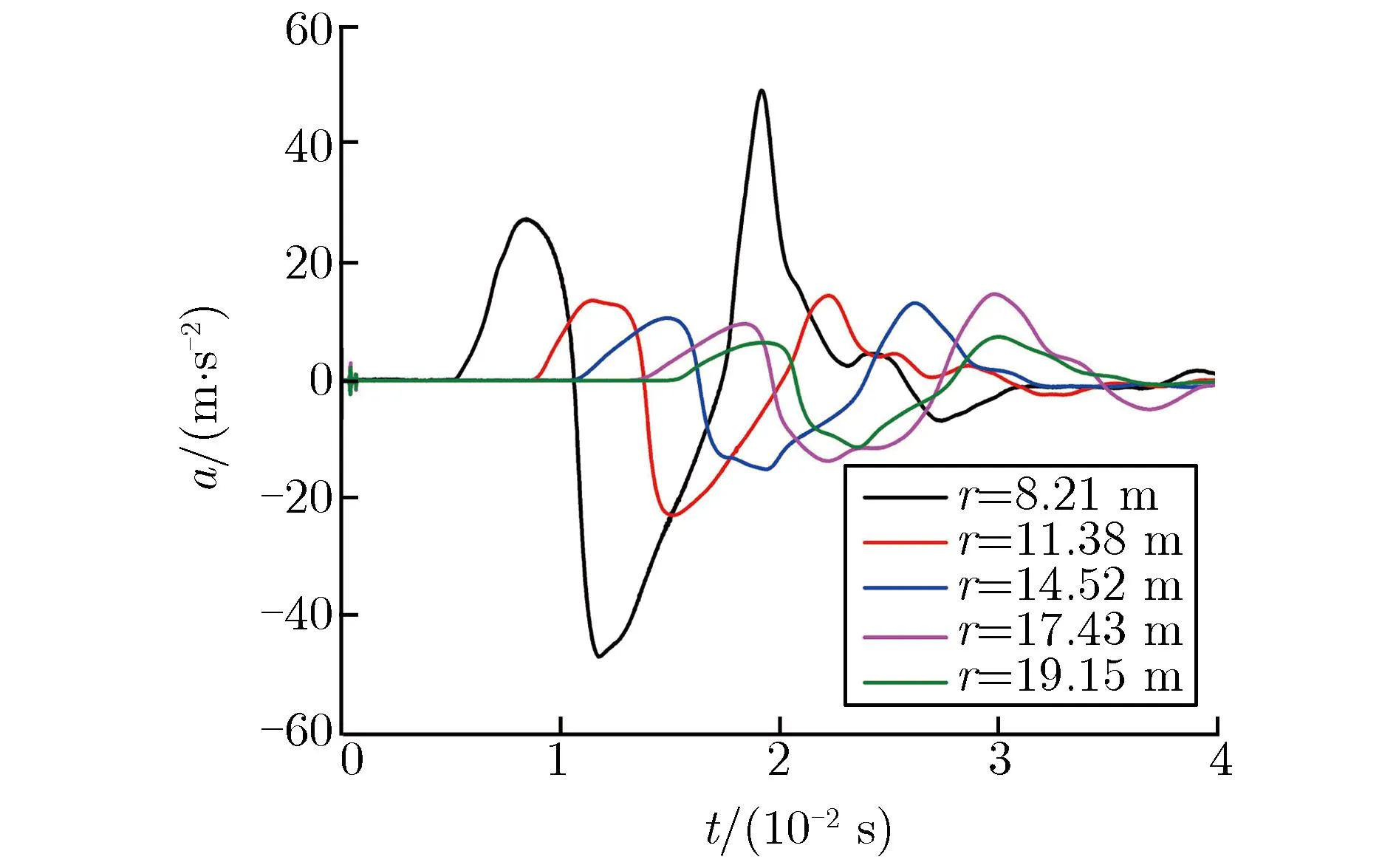
(b)S10 far field

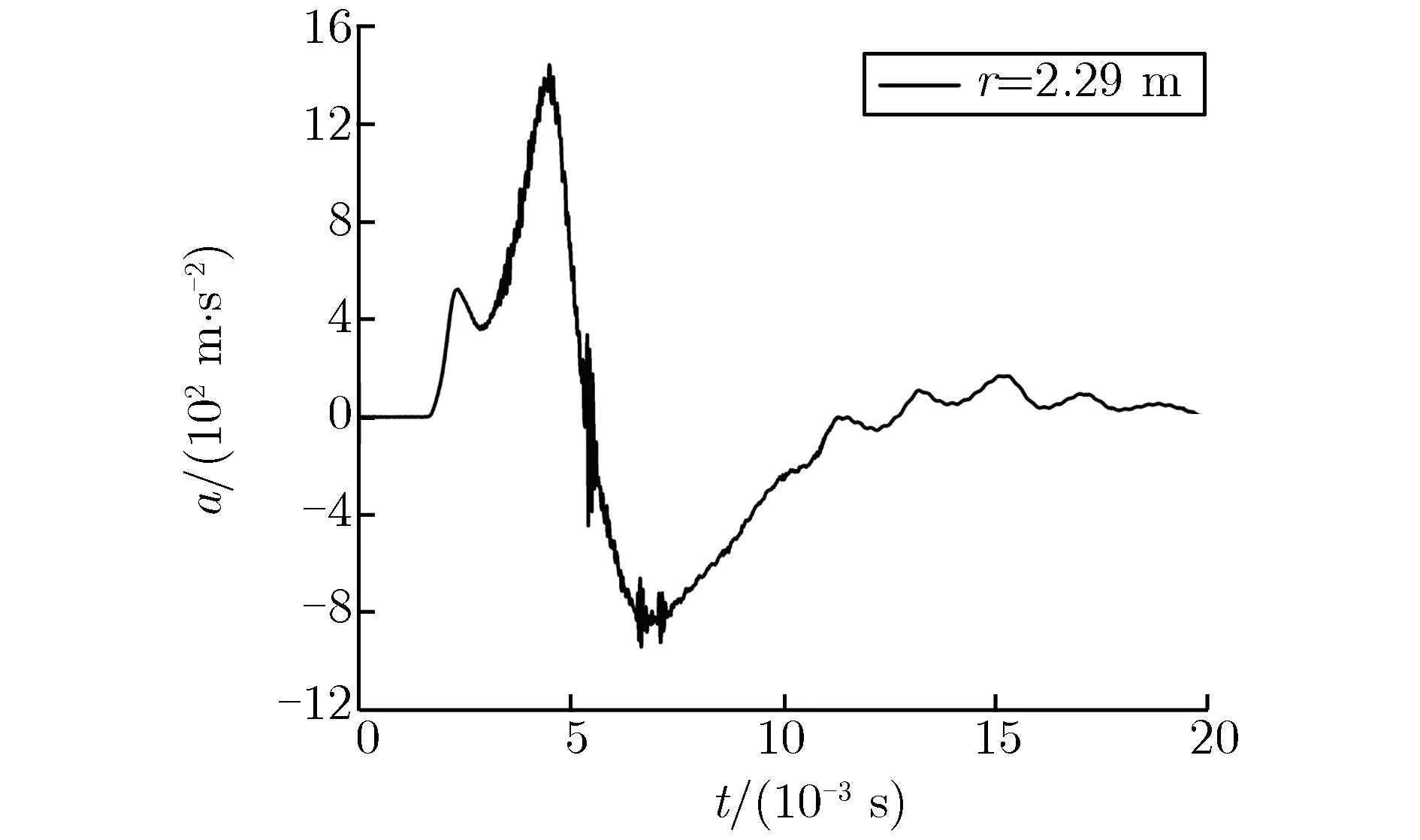
(c)S30-1 near field

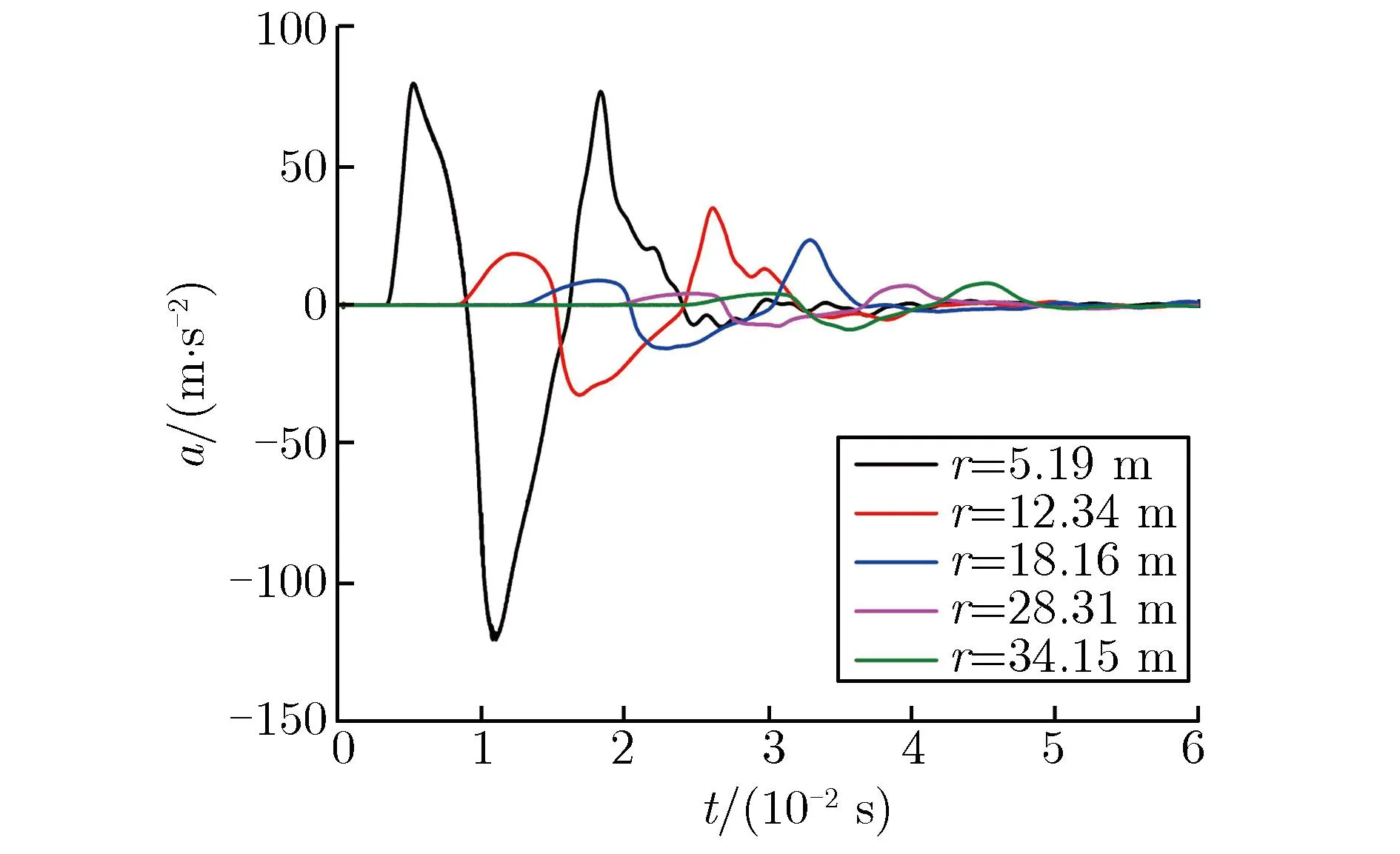
(d)S30-1 far field

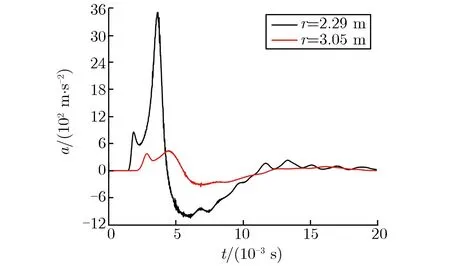
(e)S30-2 near field

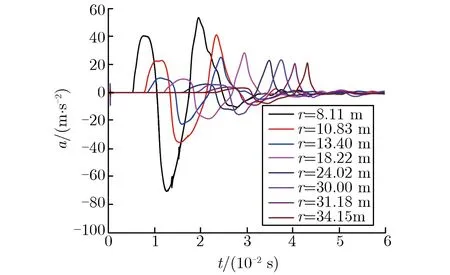
(f)S30-2 far field

(a)S10

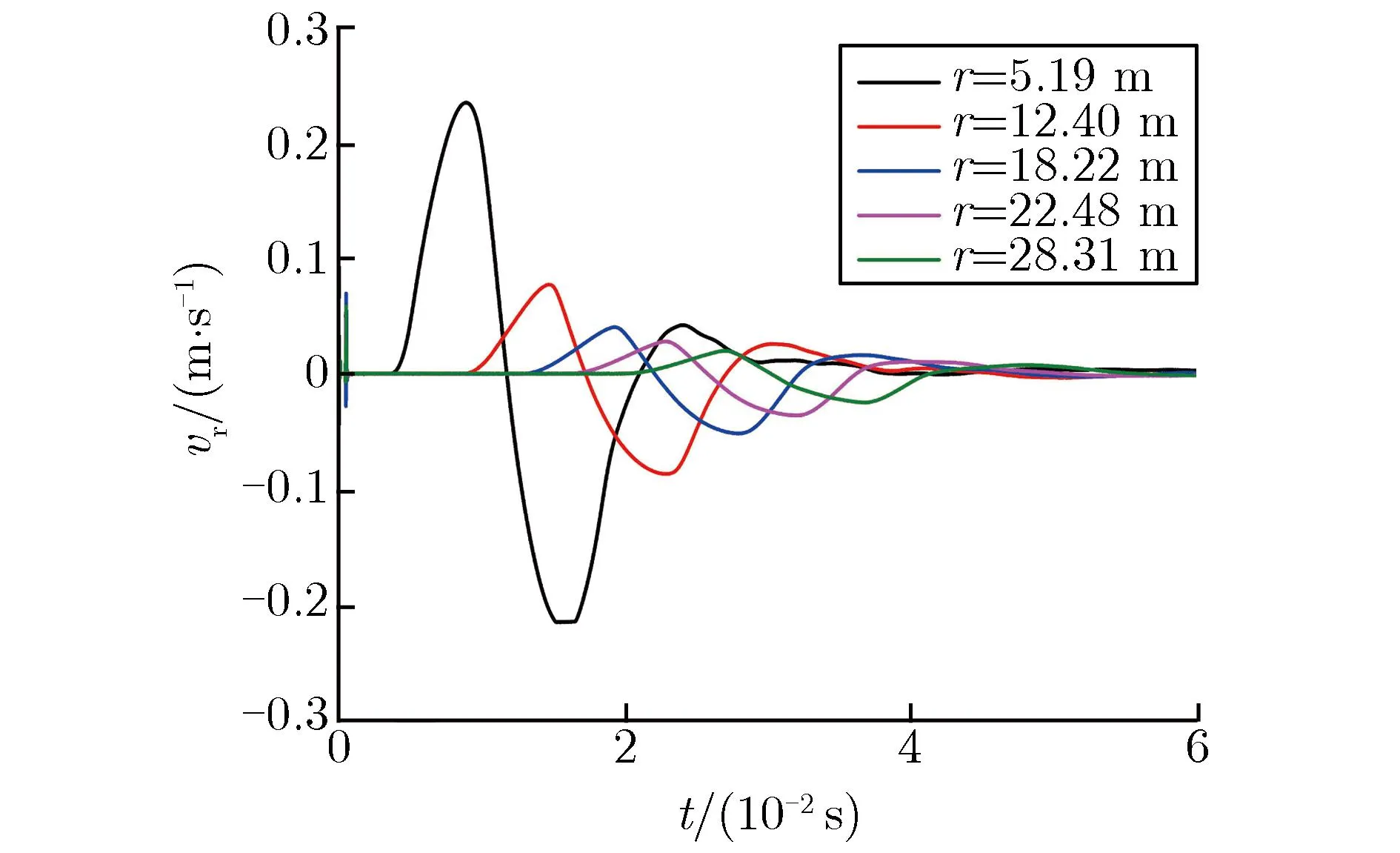
(b)S30-1

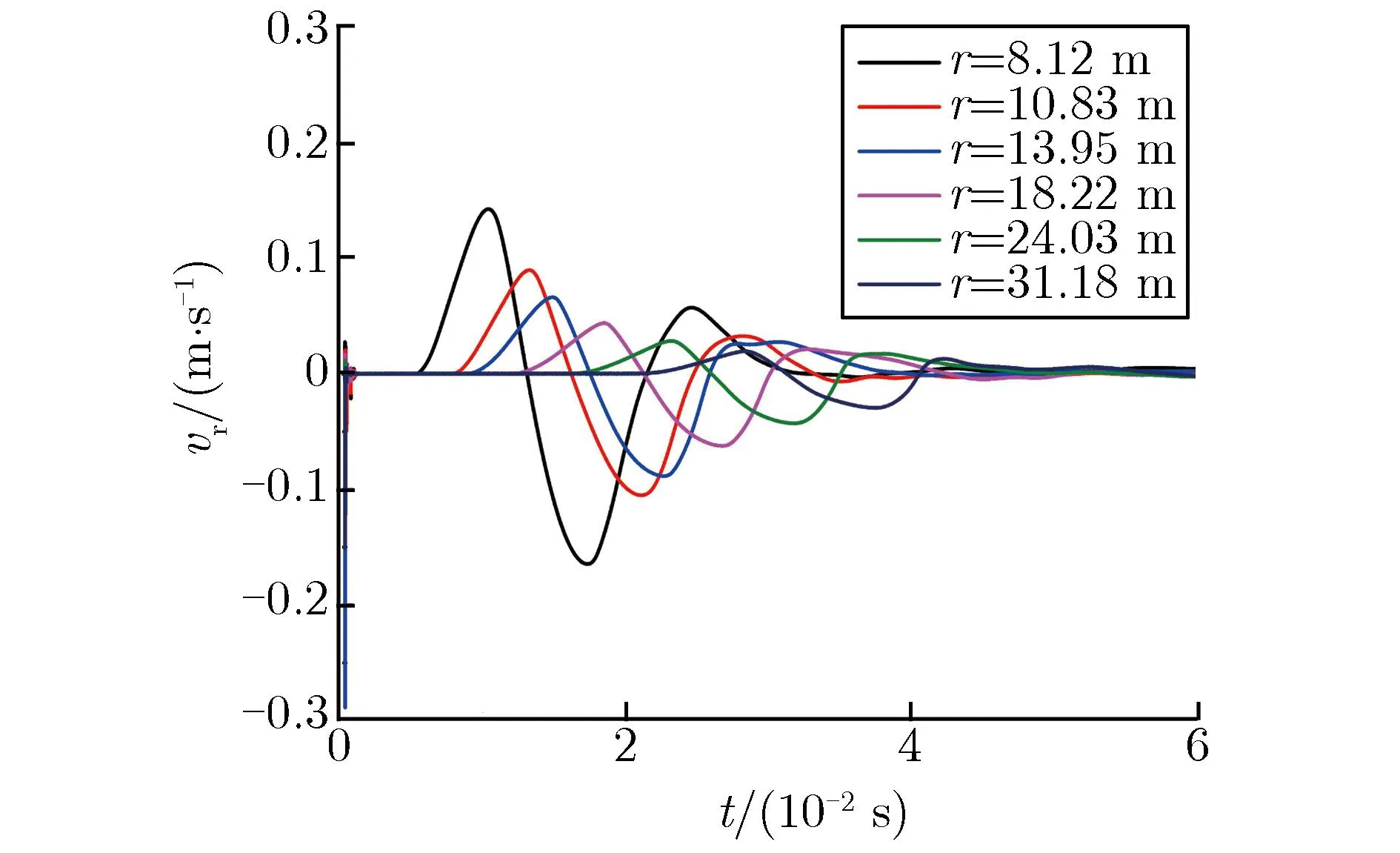
(c)S30-2

3 数据分析与讨论

3.1 自由场应力波参数峰值的衰减规律

图4-图6分别为3发实验的比加速度首峰值、粒子速度峰值和比位移峰值随比爆心距的变化关系。比加速度首峰值、粒子速度峰值及比位移峰值的拟合公式可写为

ar_FPV·Q1/3=817.71×(r·Q-1/3)-1.865

(1)

vr_max=1.13×(r·Q-1/3)-1.826

(2)

ur_max·Q-1/3=1.24×(r·Q-1/3)-1.612

(3)

其中：ar_FPV为首个径向加速度峰值,m·s-2;vr_max为径向速度峰值,m·s-1;ur_max为径向位移峰值,mm。ar_FPV的数据由所有加速度传感器实测所得;vr_max包含了所有速度传感器实测数据、实测加速度积分数据;ur_max包含了实测速度一次积分数据、实测加速度二次积分数据。

由图4-图6可见,不同当量爆炸实验测得的ar_FPV,vr_max,ur_max按爆炸相似率进行处理后,与经验拟合公式基本相符,表明自由场应力波的上述几个参数符合爆炸相似率。

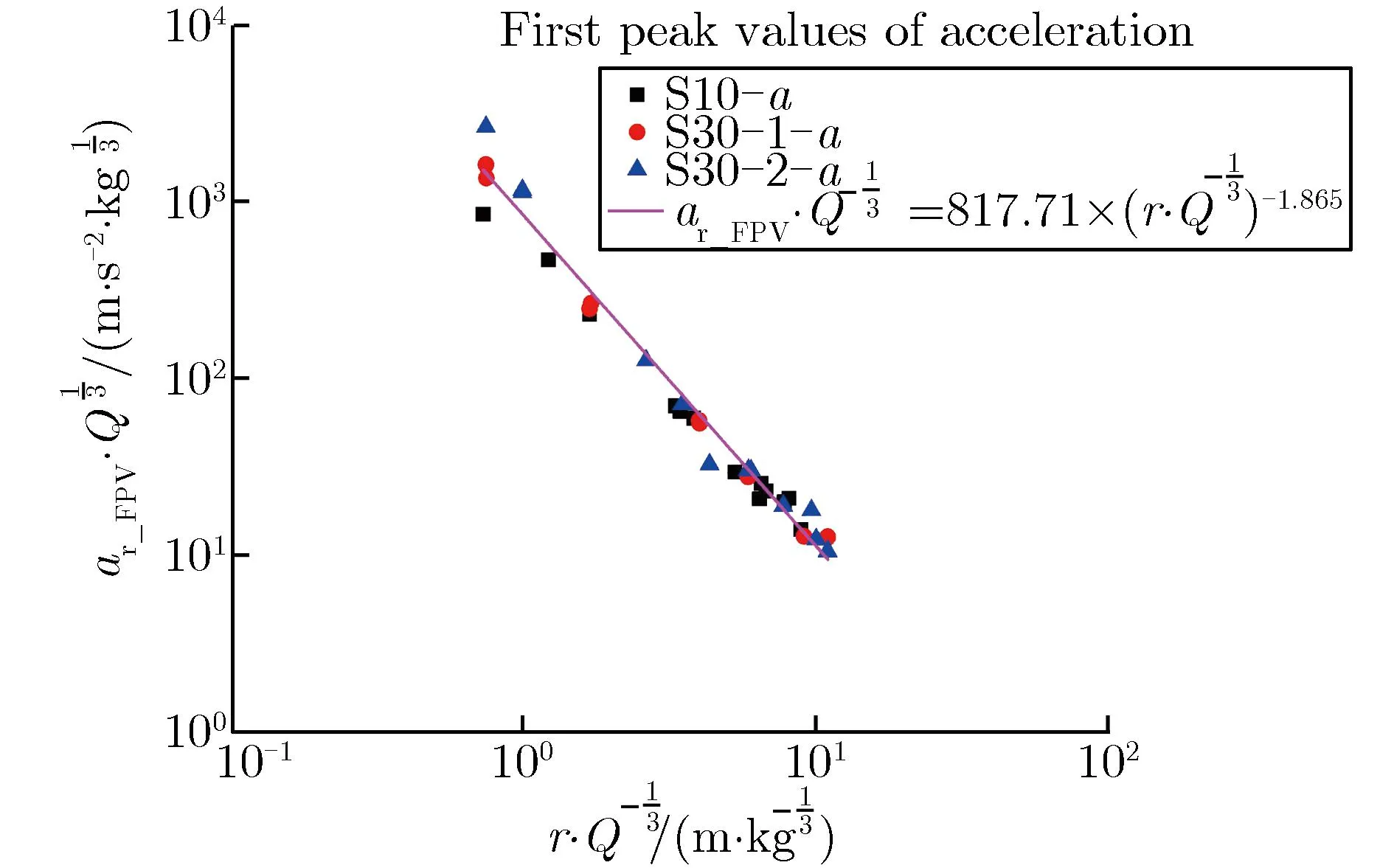
图4 比加速度首峰值随比爆心距的变化关系

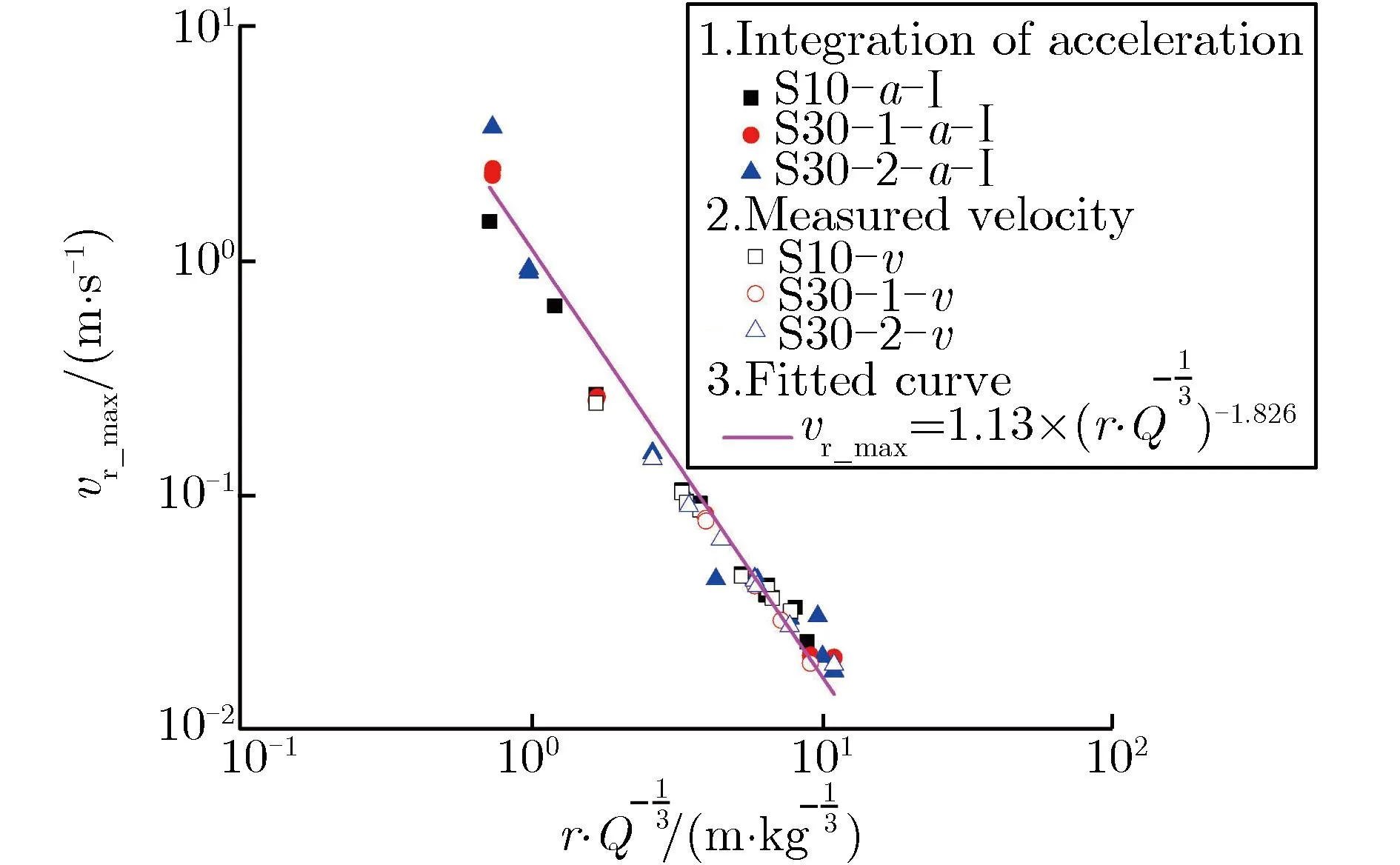
图5 粒子速度峰值随比爆心距的变化关系

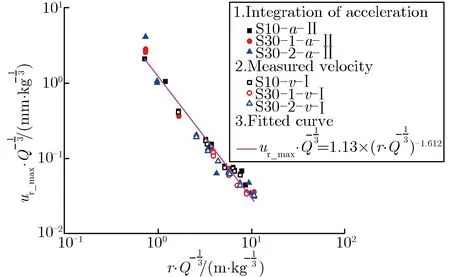
图6 比位移峰值随比爆心距的变化关系

用XM表示实测应力波参数,用XF表示对应拟合的应力波参数,则实测值与拟合值相对偏差的离散序列d可表示为

(4)

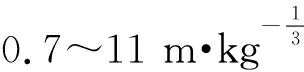
(5)

表2 实测自由场地冲击参数和经验拟合公式的相对偏差

由表2可知,实测比加速度、速度、比位移与经验拟合公式的平均相对偏差和标准偏差均小于3.4%和29.1%。在两倍标准偏差内,实测地冲击参数和拟合公式之间的关系可表示为

(ar_FPV·Q1/3)M=(0.47～1.60)×(ar_FPV·Q1/3)F

(6)

(vr_max)M=(0.43～1.58)×(vr_max)F

(7)

(ur_max·Q-1/3)M=(0.45～1.62)×(ur_max·Q-1/3)F

(8)

由式(6)-式(8)可知,置信概率为95%时,实测应力波参数基本是经验拟合公式的0.4～1.6倍。上述相对偏差包含了实验系统和场地介质本身不均匀造成的相对偏差,工程中使用这些经验拟合公式时,应充分考虑上述因素的影响,可根据式(6)-式(8),为相关应力波参数估计增加一定的保险系数。

3.2 粒子速度上升时间的特征分析

粒子速度的上升时间tr为信号起跳点至峰值所经历的时间,一般用来表征波形的变化,可反映信号的主频特征,是应力波信号分析中的一个重要特征参数。下面结合实测数据及文献中的大当量爆炸实验数据,从以下几个方面来阐述粒子速度上升时间的特征。

3.2.1 不同爆炸当量粒子速度上升时间的不相似性

利用实验中实测的粒子速度及加速度的积分,给出粒子比速度上升时间随比爆心距的变化关系,如图7所示。

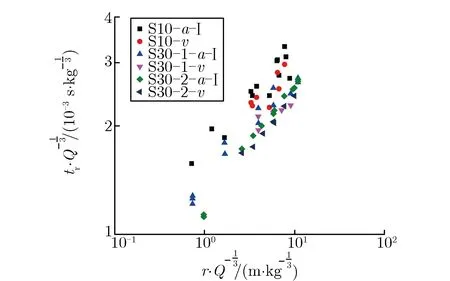
(a)S10,S30-1,S30-2

(b)Gnome,Salmon

由图7(a)可见,S10实验给出的比速度上升时间和S30-1、S30-2实验给出的结果分为较明显的两列,且S10实验给出的比速度上升时间较长。由此可知,粒子速度的上升时间不满足爆炸相似率。由图7(b)可见,美国Salmon(当量为5.3 kt TNT)和Gnome(当量为3.1 kt TNT)实验有类似的特征,小当量的Gnome实验的粒子比速度上升时间比大当量的Salmon实验长。

以某发当量为QBase的实验作为基准,则当量为Q的实验与基准实验之间的相似比λ可表示为

(9)

结合图7和式(9)可知,若用较小当量实验结果按照爆炸相似率推测大当量爆炸的实验结果,则预测的粒子速度上升时间将会偏大。

3.2.2 粒子速度上升时间与速度峰值关系的相关性

针对粒子速度上升时间不符合爆炸相似率的问题,Melosh[7]提出粒子速度的上升时间是材料属性,不依赖于爆炸当量,且上升时间tr和粒子速度峰值vr_max关系表示为

(10)

其中,A和n为材料参数。

图8为盐岩中的Salmon和Gnome实验及花岗岩中的Pile driver实验(当量为56 kt TNT)给出的粒子速度上升时间随峰值的变化关系。由图8可见,结果均与式(10)符合较好。这是Melosh认为粒子速度的上升时间不依赖于爆炸当量的重要实验依据[8]。

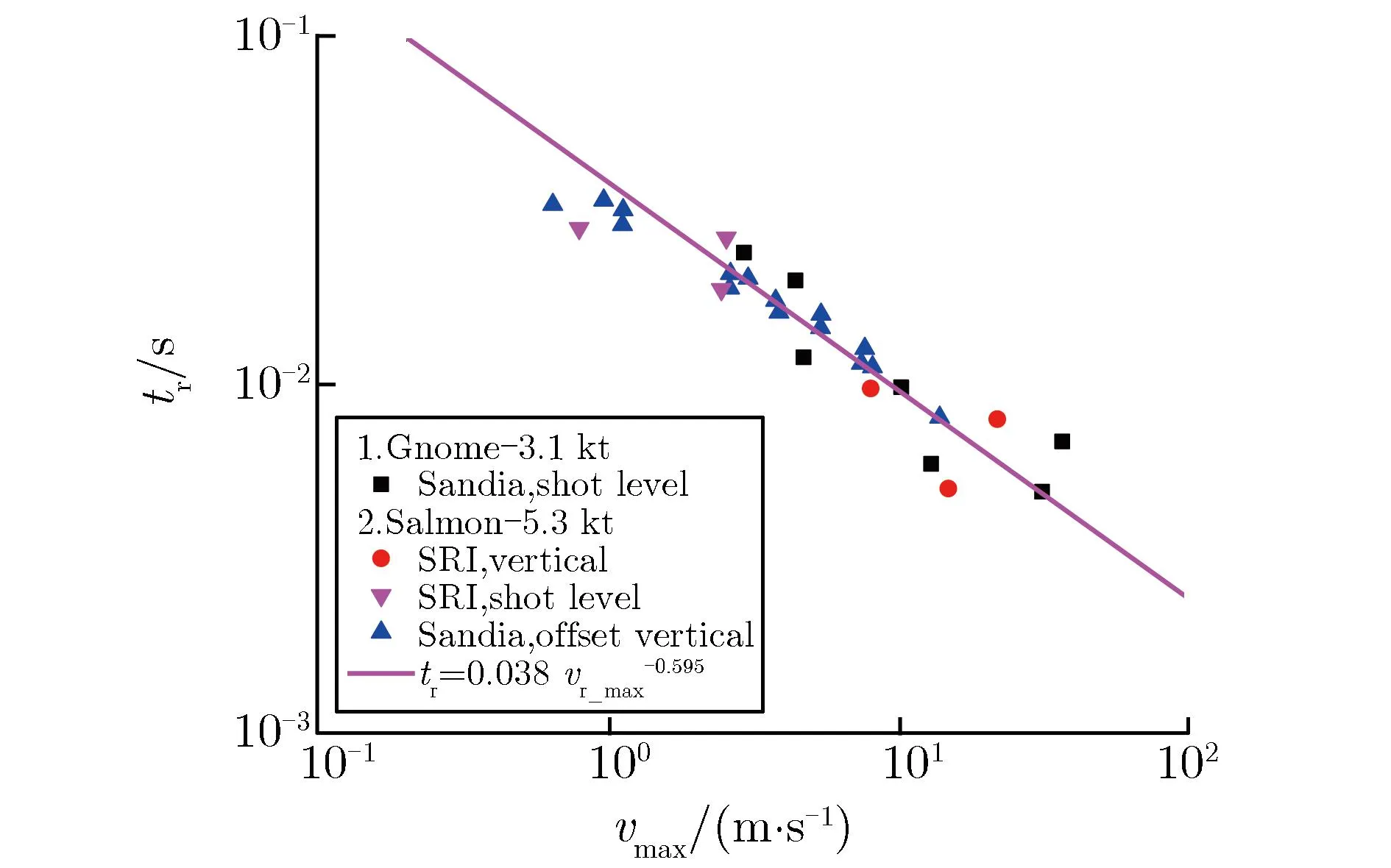
(a)Gnome and Salmon

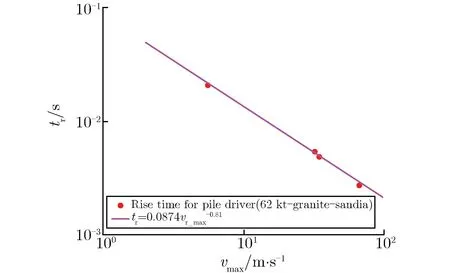
(b)Pile driver

为更深入认识粒子速度上升时间的特征,给出了冲积土中10 kg～46 kt TNT爆炸实验粒子速度上升时间随峰值的变化关系,如图9所示。由图9(a)可见,冲积土中大当量爆炸(0.5～46 kt TNT)实验的粒子速度上升时间先随着速度峰值的降低而增加,且一定程度上符合式(10)的描述。当速度峰值较低时,粒子速度上升时间随峰值降低而减少,对于冲积土中大当量爆炸的这种现象,Melosh未解释。本文结果表明,S10,S30-1,S30-2的粒子速度上升时间随峰值的变化关系与式(10)基本相符,未出现上升时间随速度降低而减少的现象。对比文献中大当量实验数据和本文10,30 kg TNT爆炸实验数据可见,粒子速度上升时间随峰值的变化规律略有不同,这可能是不同冲积土场地组分构成差异造成的。

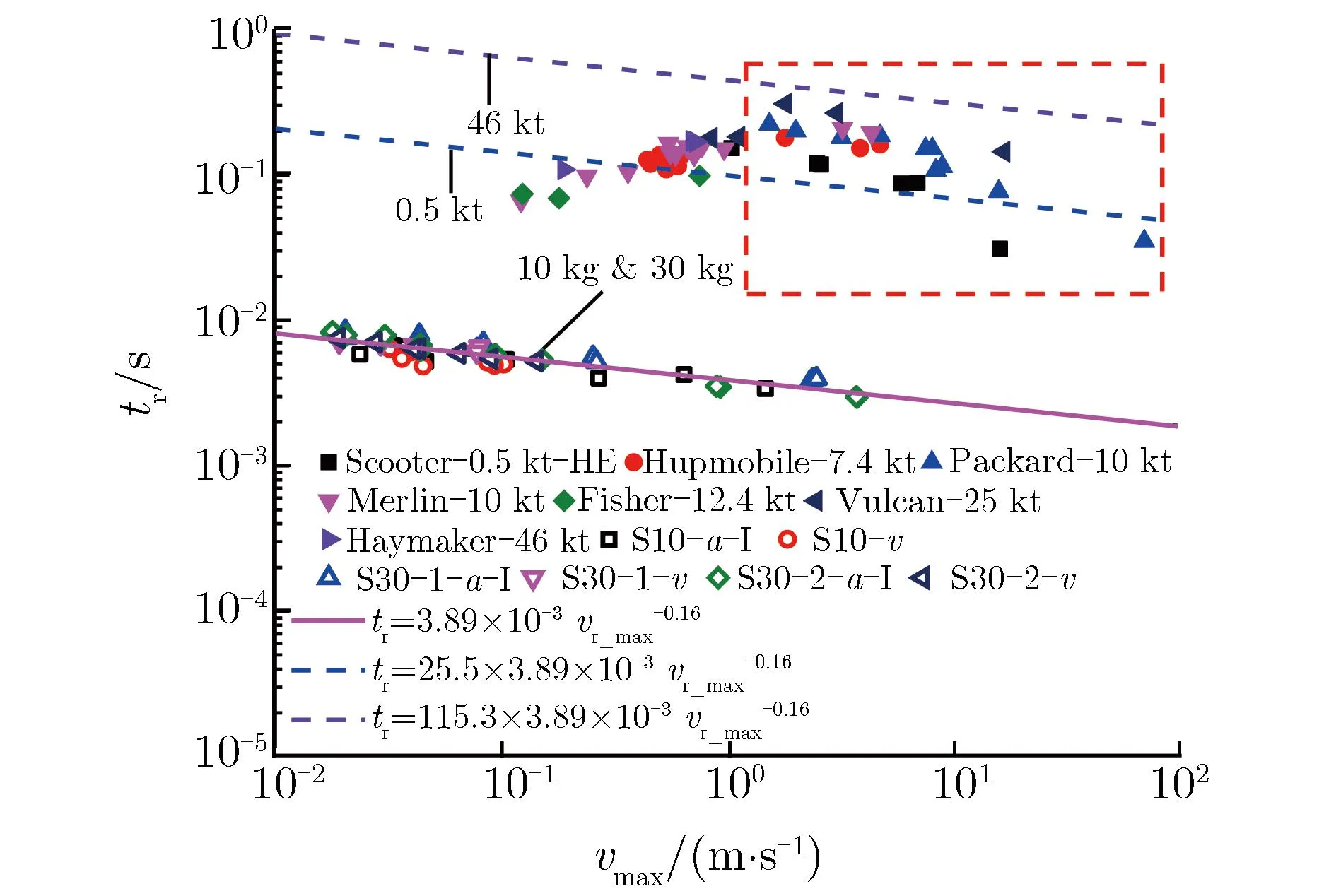
(a)Gnome and Salmon

(b)Pile driver

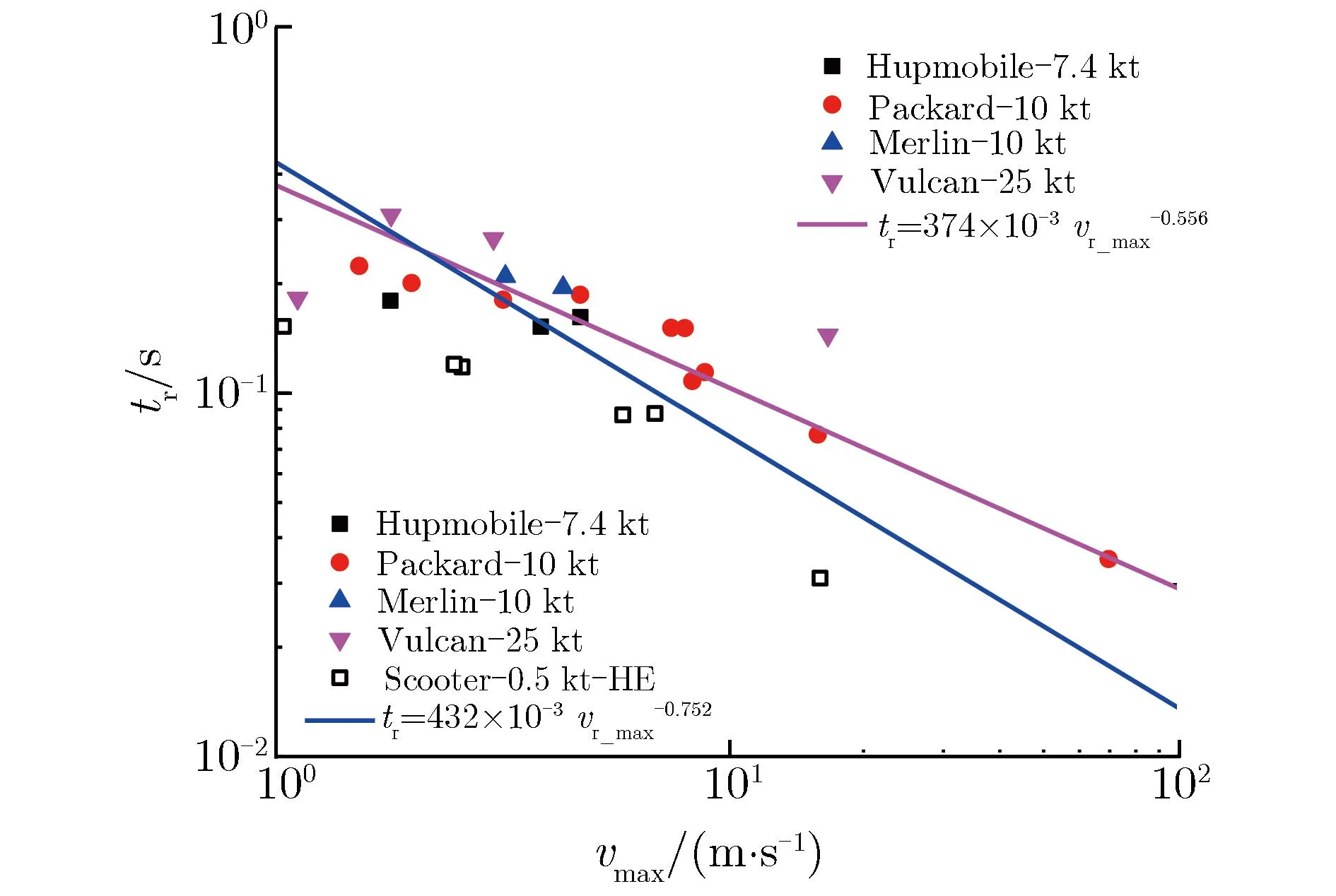
基于图8(a)和图9的数据,综合场地和当量因素,把上述数据分为No.1(Gnome,Salmon),No.2(S10,S30-1,S30-2),No.3(Hupmobile,Packard,Merlin,Vulcan),No.4(Scooter,Hupmobile,Packard,Merlin,Vulcan)4个爆炸实验组,不同爆炸实验组实测粒子速度上升时间和拟合公式的相对偏差如表3所列。这4个实验组涵盖了几十千克TNT至几十千吨TNT爆炸实验的数据。

表3 不同爆炸实验组实测上升时间和拟合公式的相对偏差

4个实验组的粒子速度上升时间tr和峰值vr_max之间的关系可拟合为

(11)

结合式(4)的定义,表3列出不同爆炸实验组实测的tr-vr_max数据点与式(11)的平均相对偏差及标准偏差。由表3可知,No.1～No.3实验组数据点的变化规律与式(10)基本相符,实测数据和拟合公式之间的离散程度大体相同。当把Scooter实验加入No.3实验组,平均相对偏差为11.8%、标准偏差为53.1%,数据集的离散程度大大增加。

根据式(5),在两倍标准偏差内,式(11)可写为

(12)

由式(12)可知,在95%的置信区间内,No.1～No.3实验组拟合公式预测的相对偏差较小,没有产生量级上的偏差,一般可用于工程预估,No.4实验组拟合公式预测的相对偏差较大,在极端情况下,拟合公式预测值(tr)F可能为实验结果(tr)M的18倍(1/0.056),这超出了正常一般工程设计的安全许可范围,工程预估使用时需慎重。

3.2.3 粒子速度上升时间的爆炸当量依赖性

把冲积土中10 kg TNT和30 kg TNT爆炸实验获得的tr-vr_max数据点,按式(10)进行拟合(如图9所示),同时把拟合曲线按照0.5～46 kt TNT进行比例换算(以30 kg TNT作为基准),得到图9(a)中的两条虚线。由图9(a)可见,冲积土中0.5～46 kt TNT爆炸实验获得的tr-vr_max数据点基本落在两条曲线附近。这说明,粒子速度的上升时间依赖于爆炸当量,而不仅仅与速度峰值相关。为进一步证实粒子速度上升时间与爆炸当量相关,给出了花岗岩中0.125 g TNT球面波实验[14]及Pile driver(当量为62 kt TNT,场地介质为花岗岩)实验的对比,如图10所示。以0.125 g TNT球面波实验为基准,Pile driver实验的相似比为7 915。在两种非常悬殊的爆炸当量下,图10中不同实验的tr-vr_max数据点清晰地分为不同列(如图10中实线所示),这说明粒子速度上升时间和爆炸当量是相关的。把0.125 g TNT球面波实验得到的上升时间,按相似比7915换算到62 kt TNT的爆炸实验(如图10中虚线所示),可见,球面波实验(0.125 g TNT)得到的tr-vr_max数据点和Pile driver实验(62 kt TNT)数据点在变化规律上符合得较好。

为进一步认识粒子速度上升时间与当量之间的相关性,把No.1～No.4实验组的最小当量实验作为基准实验,根据式(9),给出其他实验的相似比λ,如表4所列。由表4可知,以Gnome为基准实验时,Salmon实验的相似比为1.2;以S10为基准实验时,S30实验的相似比为1.44;以Hupmobile为基准实验时,Packard实验的相似比最小,为1.10,Vulcan实验的相似比最大,为1.5;以Scooter为基准实验时,Hupmobile实验的相似比最小,为2.46,Vulcan实验的相似比最大,为3.68,且Scooter实验和Hupmobile实验给出的tr-vr_max数据点已呈现出明显的分离趋势。

结合第3.2.2节的分析可知,No.1～No.3实验组中,相似比小于1.5时,各实验组对应的拟合公式均可较好反映真实的实验结果;No.4实验组中最小的相似比为2.45,实验结果与拟合得到的tr-vr_max曲线偏离最大,一般不可用于工程预估。

综上,由不同场地几十千克TNT至几十千吨TNT爆炸实验结果的分析可知,当两发实验相似比小于1.5时,不同实验获得的tr-vr_max数据点的变化规律基本一致,可用相同参数的式(10)进行拟合表征,不会引起较大偏差;当相似比大于2.46时,不同实验获得的tr-vr_max数据点具有不同的变化规律,需不同参数的式(10)进行表征。

上述分析中,基准实验为特定数据集的最小爆炸当量实验。若基准实验取为特定数据集的最大爆炸当量实验,则上述相似比为其倒数。由此可知,当爆炸当量Q为(0.3～3.4)QBase((1/1.53～1.53)QBase)时,基准实验获得的tr-vr_max曲线可用来预估爆炸实验当量为Q的tr-vr_max曲线。当爆炸当量Q大于14.9QBase(2.463QBase)或小于0.07QBase(1/2.463QBase)时,基准实验获得的tr-vr_max曲线不可用来预估当量为Q的爆炸实验tr-vr_max曲线。当爆炸当量Q处于(0.07～0.3)QBase((1/2.463～1/1.53)QBase)或(3.4～14.7)QBase((1.53～2.463)QBase)时,用基准实验获得的tr-vr_max曲线预估当量为Q的爆炸实验tr-vr_max曲线时,可能造成量级上的偏差。

4 结论

(1)冲积土中10 kg TNT和30 kg TNT地下封闭填实爆炸激发的粒子比加速度、粒子速度、粒子比位移符合爆炸相似率;在95%的置信度下,实测应力波参数的峰值约为经验拟合公式的0.4～1.6倍,在使用经验公式对地下爆炸的冲击环境预估时,应充分结合需求实际,为评估结果合理设置安全系数。

(2)从0.125 g TNT到几十千吨TNT的地下封闭填实爆炸结果看,粒子速度上升时间不符合爆炸相似率,但上升时间与粒子速度峰值和当量均有一定相关性,上升时间和速度峰值之间的关系不能视为材料自身属性;从各实验结果的分析看,当爆炸当量为基准实验的0.3～3.4倍时,可用基准实验测定的上升时间和速度峰值之间的关系来预测评估相关实验结果,超出上述范围时,预测的结果可能会造成较大的偏差。