硼中子俘获治疗剂量蒙特卡罗计算程序Magic开发与验证
2023-03-11孙爱扣陈珍平匡蓝珺高克坤刘程伟
孙爱扣,陈珍平,3†,匡蓝珺,高克坤,刘程伟,于 涛
(1. 南华大学 核科学技术学院;2. 南华大学 先进核能技术设计与安全教育部重点实验室:湖南衡阳421001;3. 苏州大学 放射医学与辐射防护国家重点实验室, 江苏苏州 215123)
恶性肿瘤现已成为导致人类死亡的头号杀手,且发病率正在逐年增加。2022年,国家癌症中心发布我国癌症患者为406.4万人[1]。目前,癌症的治疗方式主要有手术治疗、化学治疗及放射治疗。国内将近50%~70%肿瘤患者在治疗过程中接受放射治疗。其中,硼中子俘获治疗(boron neutron capture therapy,BNCT)是一种崭新的二元靶向放射治疗手段,主要原理是通过将具有选择性的含硼药物注射入人体内,让10B富集于肿瘤区,用热中子束照射10B富集区域,由于10B具有异常大的热中子吸收截面,大量的10B会发生10B(n,α)7Li反应,释放出α,7Li 2个具有高传能线密度(linear energy transfer,LET)的粒子,这两种粒子在约12~13 μm的范围内沉积能量,使沉积能量区域的细胞DNA产生难以修复的损伤,最终杀死肿瘤细胞,治疗效果优于常规治疗手段[2]。
BNCT的治疗包括计算和分析患者体内的照射剂量分布,用以确定中子射束照射时间及方向角度的最优化配置,并同时遵守危及正常组织和器官的剂量限制。BNCT中组织剂量基本来自于:(1)硼剂量。由10B(n,α)7Li反应所获得,且由于硼对热中子的吸收截面非常大(3 840 b),释放能量多,因而硼剂量对总剂量的贡献很大,为主要剂量;(2)热中子剂量。热中子与人体中的14N原子发生核反应生成反冲核14C和质子,在人体细胞中沉积能量所产生的的剂量;(3)超热中子及快中子剂量。统计的是除热中子外所有中子由弹性散射而沉积的能量;(4)光子剂量。主要有伴随入射中子束产生的γ射线、硼中子俘获反应中产生的射线及热中子与人体内的H原子发生俘获反应生成的γ射线3种来源。上述4种剂量单元的计算非常复杂,目前尚无精确剂量计算的相关经验公式,现阶段BNCT的治疗计划系统中主要采用蒙特卡罗模拟计算患者或体模的个体化模型剂量[3]。目前,国际上针对BNCT的治疗计划系统(treatment planning system,TPS)日渐成熟,开发了多种治疗软件,主要有:美国的NCTPlan和SERA、日本的JCDS、北京应用物理与计算数学研究所研制的MCDB及中硼医疗公司研发的NeuMANTA等[4]。
本文基于成熟的蒙特卡罗方法研制了自主化BNCT蒙特卡罗剂量计算程序Magic。针对国际基准题Snyder修正头部模型,在此基础上添加一个假设的肿瘤模型,建立1 mm精细体素模型来逼近解析模型,并在程序中采用网格中心点方法填充体素模型材料,同时对中子源、Kerma因子及S(α,β)热散射等参数设置,使用MCNP和Magic程序进行模型深度-剂量率曲线模拟对比,对结果进行分析研究,初步验证了Magic程序正确性,并以Magic为基础,研究10B药代动力学模型下的硼浓度对BNCT剂量学影响规律,可为BNCT 剂量计算基准化和临床实践应用提供参考。
1 蒙特卡罗剂量计算程序Magic开发
目前,国际上BNCT治疗计划系统的剂量计算引擎主要使用MCNP作为核心计算传输工具,然而MCNP的禁止转让限制了其在中国的使用。剂量计算是整个BNCT治疗计划系统的核心部分,MCNP的限制将影响国内自主化BNCT治疗计划系统的发展,同时MCNP程序体系庞大,主要用于核能、核工程及核技术等各领域的相关理论计算研究,并不适用于特殊研究需求的发展。鉴于此,本文基于蒙特卡罗粒子输运方法自主开发了BNCT治疗计划系统专用计算引擎—蒙特卡罗剂量计算程序Magic。Magic主要采用C++开发,借助于C++丰富的标准库和第三方库,覆盖了多个可扩展功能,便于未来的BNCT治疗计划系统的发展和维护。
Magic程序由7块功能模块组合构成,包括几何模块(Geometry Module)、源项模块(Source Module)、数据库模块(Database Module)、粒子输运模块(Particle Transport Module)、计数模块(Tallies Module)、输出模块(Output Module)和辅助模块(Auxiliary Module),图 1为Magic开发框架。几何模块主要采用面方程描述方法构造复杂的剂量计算模型,基于组合几何(CSG)方法进行几何描述,同时支持基于Lattice重复结构的超精细毫米量级体素(voxel)建模,并对相应组织区域从数据库模块中填充组织材料的核素成分及比例;源项模块旨在设置粒子的初始条件和源的属性,如源的空间分布、能量分布、角度分布及粒子类型等信息,并对相应源参数支持多种概率分布抽样(离散、连续、直方图及混合),满足模拟BNCT复杂中子源的要求;数据库模块储存了基于ENDF/B-VIII.0评价数据库,利用具有层次结构,可处理大数据集等优点的HDF5数据格式来存储粒子输运中物理相关的各反应截面数据[5],同时根据ICRU46文和ICRU63文内容[6-7],创建了包括106种人体组织成分材料库和相应的Kerma因子库,并提供了支持修改和编辑相关数据的功能;粒子输运模块主要处理程序模拟粒子从产生到消失的过程,中子与物质相互作用主要涉及到弹性散射、非弹性散射及吸收,其中,吸收包含BNCT所关注剂量相关反应(n,α),(n,p),(n,γ)等,在此过程中由中子产生的次级光子将被储存在粒子库中,为后续的光子输运做好准备,光子与物质相互作用主要考虑光电效应、电子对效应、相干散射及康普顿散射;粒子输运完成后,调用计数模块,根据用户的需求,设置不同的统计参数,包括感兴趣区域、能量区间和粒子类型等,以获取相应的注量,结合数据库模块中的Kerma因子库,得到剂量;最后通过输出模块对BNCT治疗中关注的各种剂量,包括硼剂量、热中子剂量、超热中子剂量、快中子剂量、光子剂量及总相对生物效应剂量进行统计,并提供可视化处理;辅助模块为上述模块提供相关函数库及异常捕获等。
Magic程序以粒子输运模块为核心,与上游的几何模块、源项模块及截面模块相互连接,同时支持下游的计数模块和输出模块。各模块之间相互独立,且模块间通过接口进行消息传递实现各模块功能,利于程序维护和扩展。
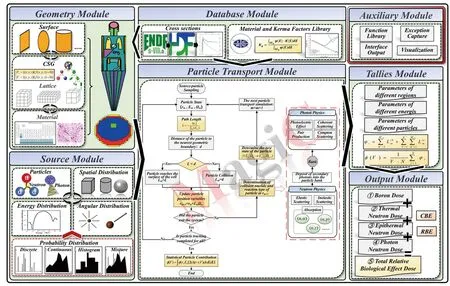
图1 Magic开发框架
2 模型及方法描述
2.1 Snyder修正头部模型
目前,国际上对于BNCT剂量理论计算普遍采用的基准问题为Snyder修正头部模型,由3个椭球面来界定不同组织的边界,将头部由里到外分为脑组织、颅骨及头皮组织3部分。整个头部又被空气包围,通常称为解析模型[3]。各分界面满足的3个椭圆面解析方程可表示为
脑组织与颅骨边界:
(1)
颅骨与头皮组织边界:
(2)
头皮组织与空气边界:
(3)
但在实际情况中,由于患者肿瘤形状、位置及大小各不相同,无法使用解析方程去描述模型,因此在国际临床中,普遍使用连续均匀的立方体网格模型来逼近模型结构,通常称为体素模型。目前Snyder修正体素模型网格尺寸通常取4,8,16 mm,当构建的体素网格越小,越能更好地趋近解析模型。故本文利用Magic构建1 mm×1 mm×1 mm精细Snyder体素模型,共分224(x方向)×224(y方向)×224(z方向)=11 239 424个体素网格,验证正确性的同时,也对Magic构建千万网格数的承载力提出考验。模拟计算的同时,在脑组织中加入半径为1.5 cm的球面作为肿瘤边界,模拟实际临床中脑部胶质肿瘤的情形。本文所模拟的含肿瘤Snyder修正模型如图2所示。
含肿瘤Snyder修正模型中脑组织、颅骨及头皮组织的元素成分和密度由Magic数据库获得,肿瘤详细的组织成分参考文献[8]。目前临床试验要求,肿瘤细胞的10B浓度必须大于正常组织细胞的2.5倍,故本文设置头皮组织及脑内正常组织硼浓度为10-5,肿瘤组织内的硼浓度为3×10-5,颅骨内不含硼[9-10]。对解析模型中材料,可精确填充描述,但对网格模型,会因网格在两种物质交界面处难以处理,传统处理方式通过得到每个立方体网格内部不同材料精确的体积比填充,当网格数量较多时,材料填充极其耗时且会带来一定偏差。为降低模拟问题的复杂度,在Magic程序模型构造中使用网格中心点的方法,根据每个网格的中心点位置确定材料密度,能大大降低材料数目,可由原来的286种材料降低至4种材料[11]。
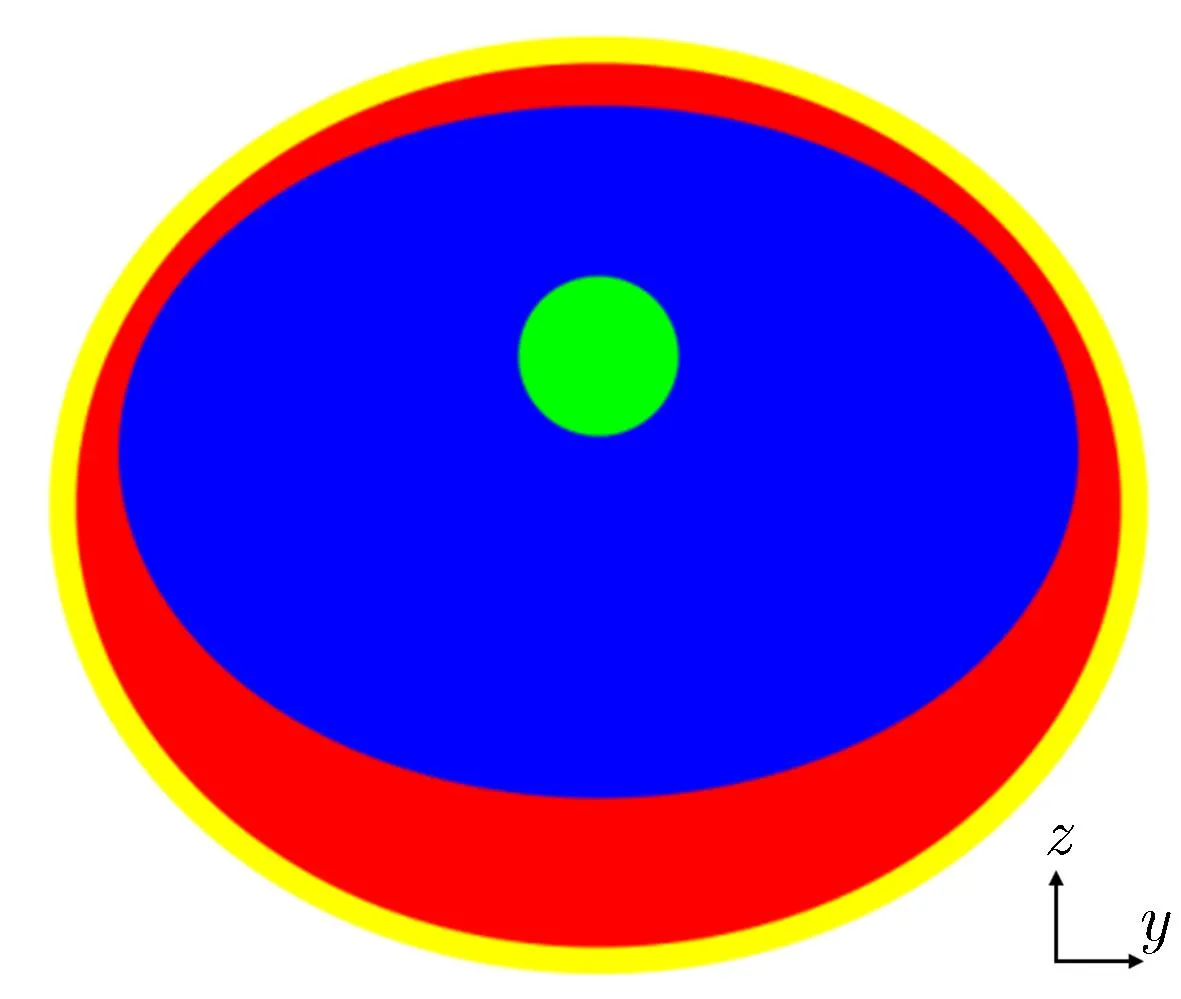
(a)Tumor modified Snyder analytical model
2.2 相对生物学效应剂量
由于不同种类的电离辐射会导致生物体产生不同的生物效应,BNCT涉及多个不同辐射剂量组分的混合场照射,因此,对BNCT治疗须衡量每种剂量组分的相对生物学效应剂量,评估其对正常组织细胞和肿瘤细胞的杀伤效应。用实验测量的相对生物学效应(relative biological effectiveness,RBE)来表征热中子剂量、超热中子及快中子剂量与光子剂量的生物学效应高低。对于硼剂量的评估,须考虑α粒子和7Li离子的RBE及10B在组织和细胞中的微观几何位置对生物学效应的综合影响,被称为复合生物学效应(compound biological effectiveness,CBE)[12]。将上述4种剂量成分分别乘上各自对应的加权因子得到总相对生物学效应剂量H,表示为
H=WBDB+WγDγ+WnDn+WPDP
(4)
其中:WB为硼剂量的CBE因子;Wγ,Wn及WP分别为光子、快中子及氮俘获产生热中子剂量的RBE因子;DB,Dγ,Dn,DP分别为硼剂量、光子剂量、快中子剂量及氮俘获产生的热中子剂量。为使本文计算结果与国际上BNCT剂量结果具有可比性,选取肿瘤及健康组织不同剂量成分的RBE和CBE因子[13-16],如表1所列。
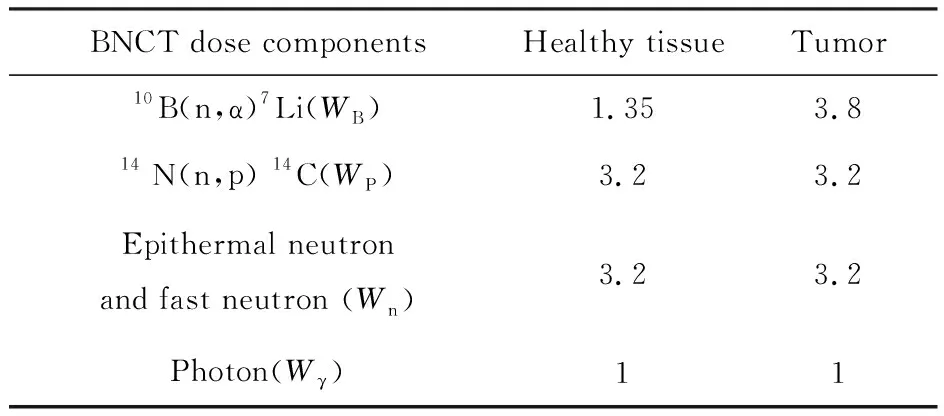
表1 肿瘤及健康组织不同剂量成分的RBE和CBE因子[13-16]
2.3 中子源设置
合适的中子源是BNCT治疗肿瘤成功的关键要素之一,理想情况下,需选择不同中子源来治疗不同深度处的肿瘤。BNCT剂量计算中,要对入射源项粒子束的类型和形状、粒子源的种类、粒子束能量及方向等参数进行详细描述。本文采取国际上针对Snyder修正模型所提出的宽谱超热混合中子束,其中能量小于0.5 eV的热中子占10%,0.5 eV~10 keV的超热中子占89%,10 keV~2 MeV的快中子占1%,总体中子源能谱服从1/E(E为中子能量)分布,均匀分布在5 cm的圆盘面上,源强度为1010cm-2·s-1。
2.4 其他相关参数的设置
由于BNCT剂量计算时涉及中子-光子耦合输运过程,剂量可通过注量率与Kerma因子得到,表示为
(5)
其中:φ(j,E)为第j个体素网格,能量为E的归一化注量率;V(j)为第j个体素网格的体积;K(j,E)为j个体素网格,能量为E的中子/光子剂量转换因子,即Kerma因子。本文采用ICRU63给出的相对于ICRU46成年人脑的Kerma因子,但该Kerma因子所对应的最低能量为0.025 3 eV,而对于BNCT的剂量来说,低于0.025 3 eV能量的中子对热中子剂量的贡献非常重要,故本文采取双对数插值,将低于0.025 3 eV对应的Kerma值外推到0.000 1 eV对应的数据,本文中光子的Kerma因子基于Seltzer[17]所计算的质能吸收系数得到。
低能中子对BNCT的剂量贡献很大,但当中子能量降低到几个电子伏时,散射靶核的热运动会对碰撞产生强烈的影响,从而对出射中子的能量及出射角度都会造成影响,最终会导致结果产生偏差。MCNP对于这种情况提供了S(α,β)热散射模型,直接调用相应核素的S(α,β)热散射模型数据即可[18],本文Magic采取相同的S(α,β)热散射模型处理Snyder材料中H的热中子散射。
3 数值验证
3.1 MCNP与Magic计算结果比较
由于MCNP程序通常可作为各类蒙特卡罗计算的“标准”,常常用于标定其他蒙特卡罗程序的准确性测试,尤其是MCNP已成熟运用在BNCT的治疗计划中。本文利用MCNP程序计算模拟Snyder解析模型的各剂量率作为标准,使用Magic程序采用上文参数设置模拟同一解析模型,比较二者计算结果的差异,并在此基础上继续利用Magic程序对1 mm千万量级体素网格的Snyder模型进行模拟,将模拟结果与MCNP解析模型结果进行比较。本文重点在于探究Magic程序的正确性,对模型沿z轴统计相关剂量,其中每个统计点的计数网格大小设置为1.6 cm×1.6 cm×0.4 cm。在实际BNCT治疗中有部分光子由中子源伴随产生的,这部分光子是无法避免的,本文假设中子源无伴随光子污染,只讨论中子与体内的核素发生反应所产生的次级光子。
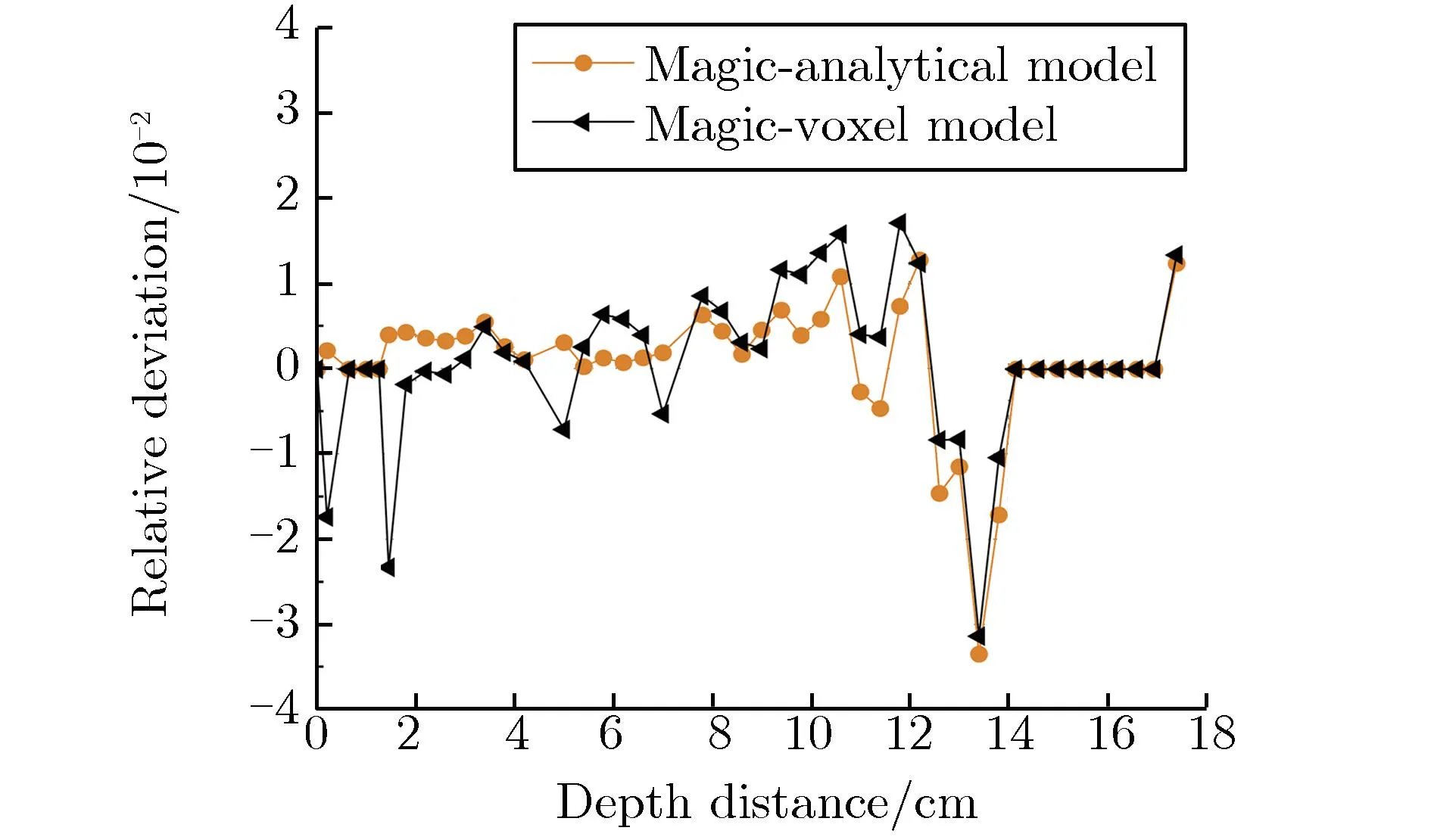
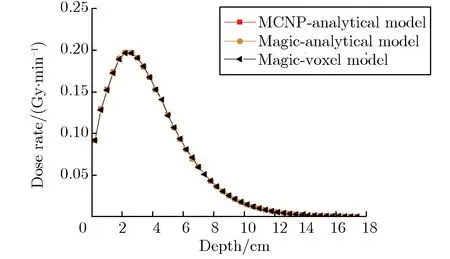
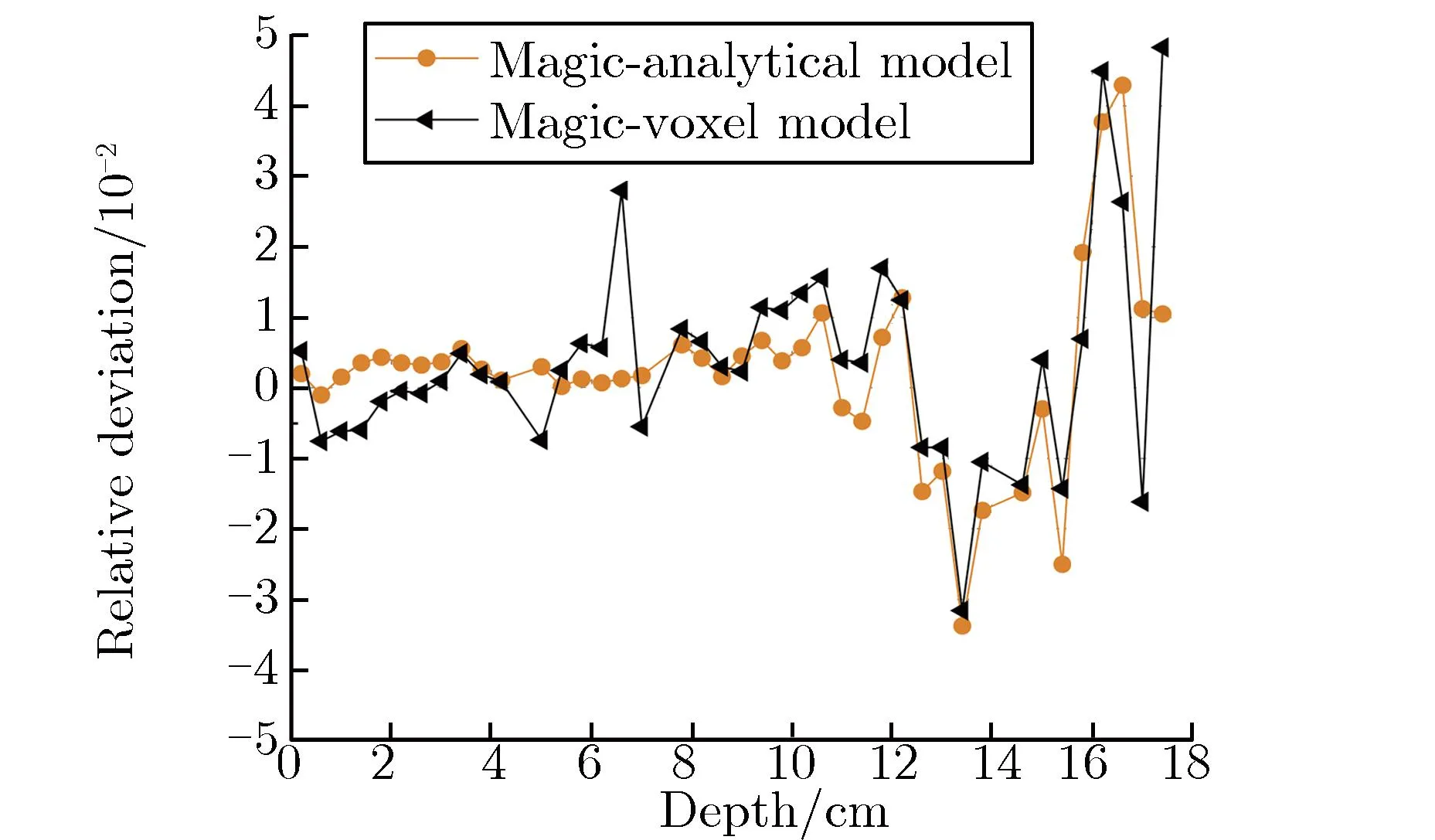
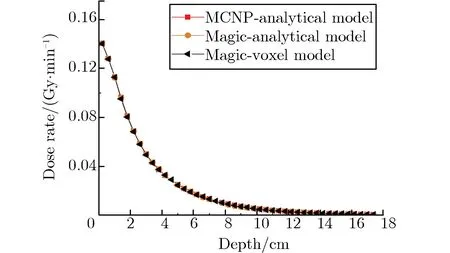
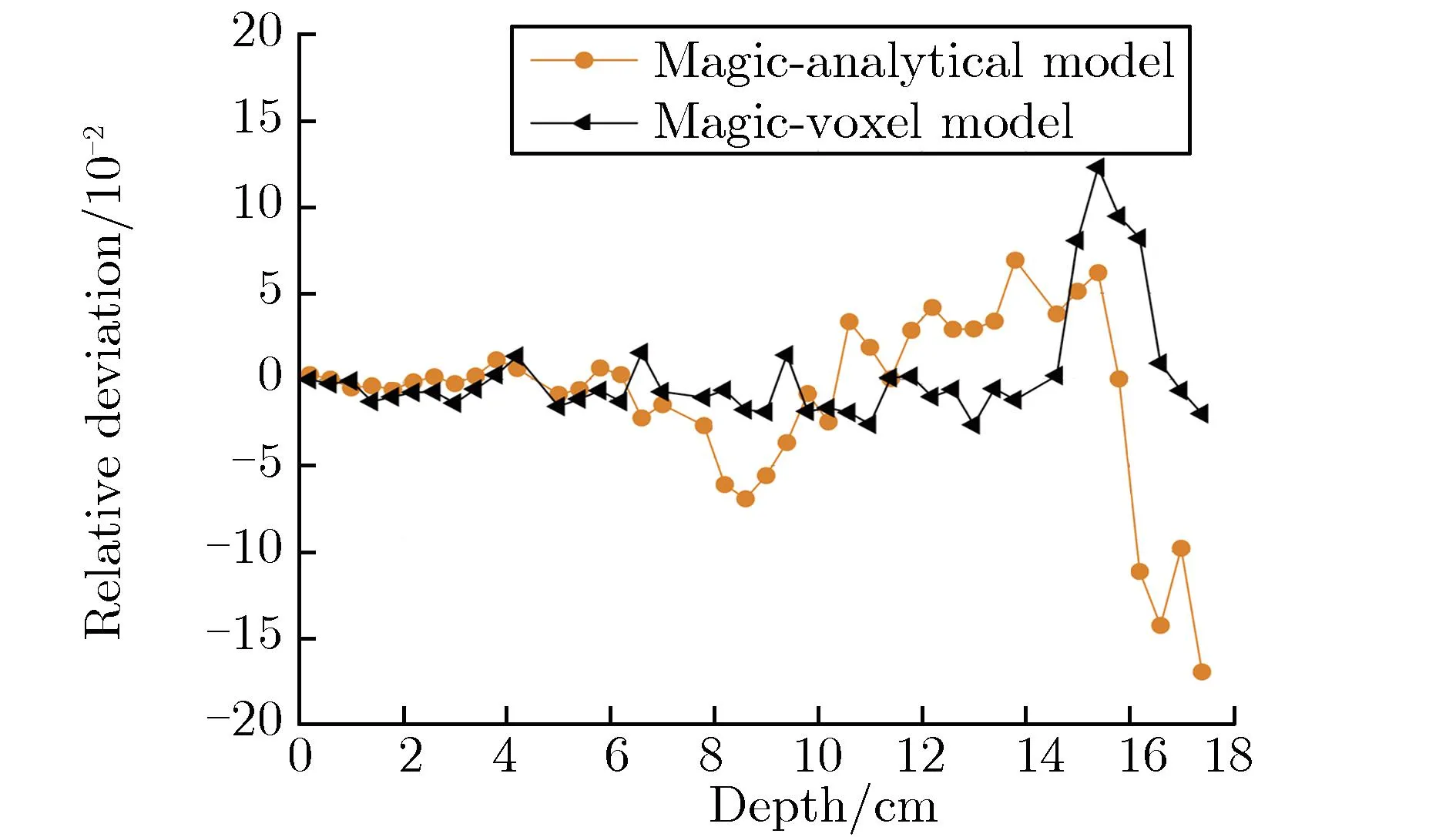
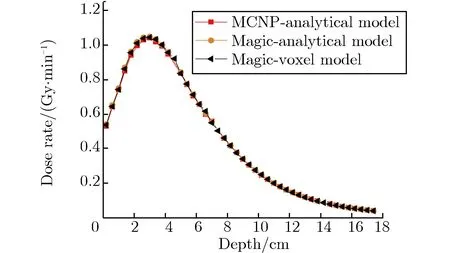
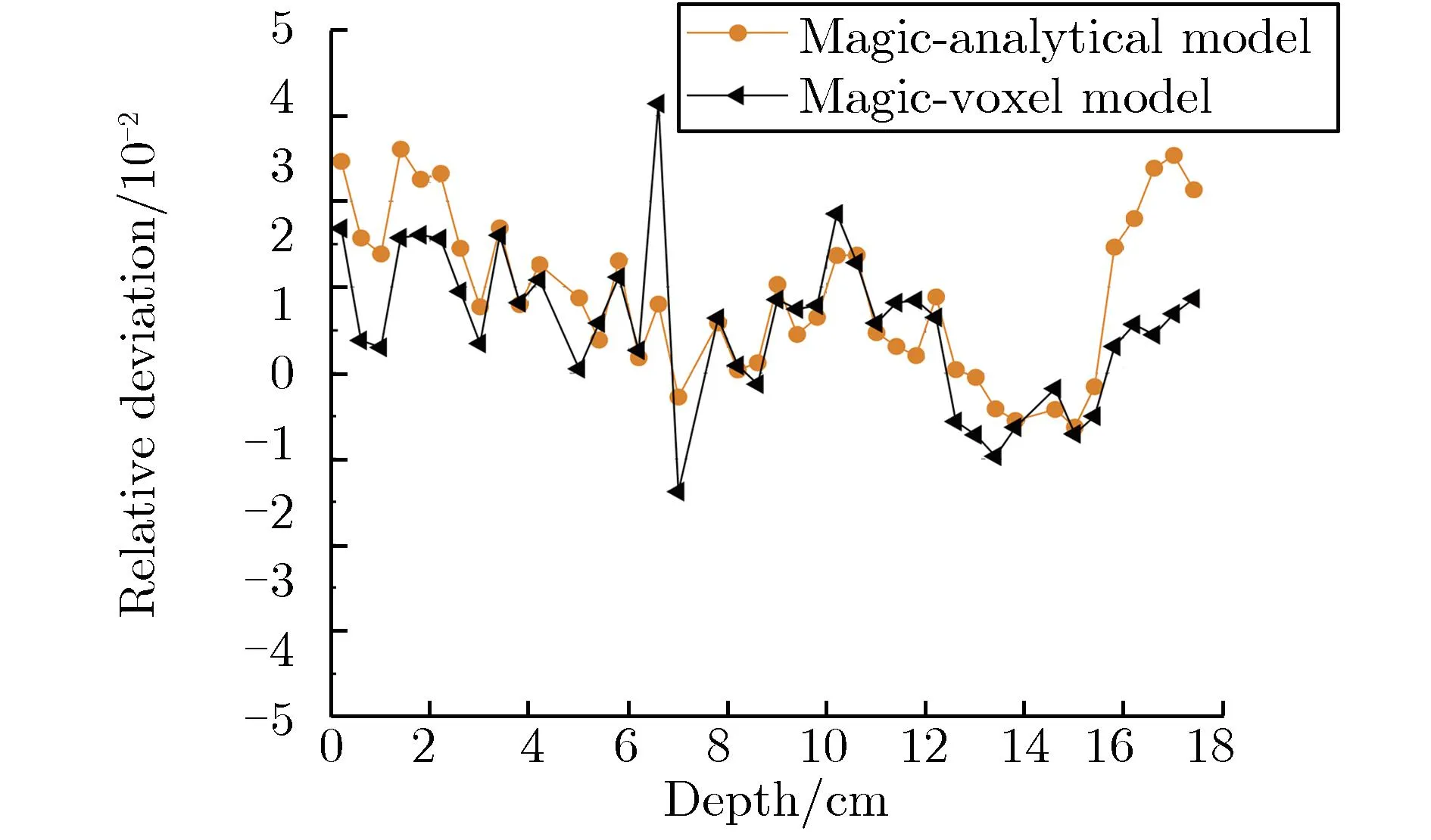
为减小蒙特卡罗程序的深穿透所带来的结果影响,两个蒙特卡罗程序输运模拟的粒子数均为1×108,确保样本数量充足。图3-图7分别为硼剂量率、热中子剂量率、超热中子及快中子剂量率、次级光子剂量率和总的相对生物效应剂量率及相对偏差随深度的变化关系。相对偏差是以MCNP解析模型结果为标准值,Magic的解析/体素模型的结果与之比较得到的偏差百分比。
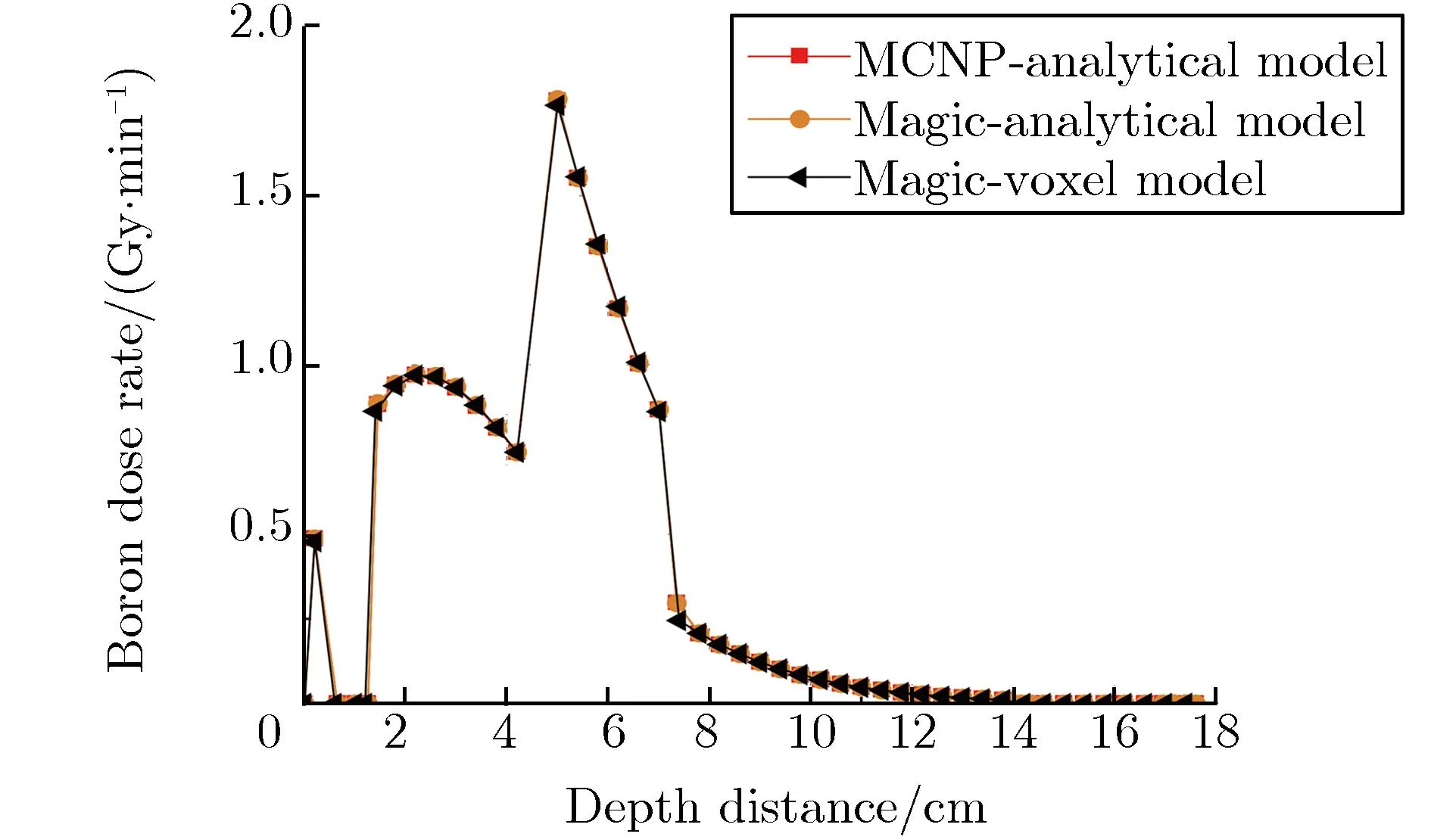
(a)Dose rate vs. depth
(b)Relative deviation vs. depth
(a)Dose rate vs. depth
(b)Relative deviation vs. depth
(a)Dose rate vs. depth
(b)Relative deviation vs. depth
(a)Dose rate vs. depth
(b)Relative deviation vs. depth

(a)Dose rate vs. depth
3.2 结果分析
由图3(a)可见,深度为0.5~1.5 cm,14~17 cm处为颅骨,由于颅骨不含硼,故没有硼剂量率,这两处的相对偏差为0;深度为4.5~7 cm时,分布曲线上的陡然变化是由于该处为肿瘤区域,硼含量较高,导致硼剂量率显著增加,有助于在临床中更精确地确定肿瘤的位置。由图3(b)可见,相对偏差保持在BNCT临床允许的5%以内[19-20]。由图3(a)、图4(a)和图6(a)可见,分布曲线趋势一致,这是由于次级光子来自于中子反应,中子剂量越多的地方产生的光子也越多,在头部的浅表组织产生的损伤最大;由图3(b)、图4(b)和图6(b)可见,相对偏差也均保持在5%以内。由图5(a)可见,因中子源发射大部分为超热中子,一开始就发生中子慢化到热中子,随着深度的加深,剂量率逐渐降低,深度小于12 cm时,相对偏差都基本保持在5%以内;深度大于12 cm时,为深穿透问题,蒙特卡罗程序计算时到达深处的粒子数较少,造成统计结果相对偏差较大。最后,将图3-图6的剂量率按照相应的权重因子整合,得到总相对生物效应剂量率,如图7(a)所示。由图7(b)可见,相对偏差均保持在5%以内。总体上,由图3-图7可见,Magic的解析模型与体素模型的模拟计算结果和MCNP解析模型的结果符合较好,表明Magic的计算结果是正确的。
4 基于Magic的BNCT动态硼浓度分析
中子注量率及硼浓度共同决定了BNCT沉积在组织中的剂量,因此在计算剂量时,这二者对剂量评估的准确性有很大的影响。目前在进行理论BNCT的治疗计划评估时,对肿瘤和正常组织的硼浓度设置都是时间固定不变的,但实际给药后组织和血液中的硼浓度会因新陈代谢随时间而变化,因此为临床剂量评估的准确性,有必要输运计算时建立10B的药代动力学模型。本文基于已验证正确性的蒙特卡罗剂量计算程序Magic定量研究动态硼浓度下BNCT剂量学规律,为临床应用的安全性提供理论基础。
目前,在BNCT含硼药物BSH和BPA上,所使用的血硼浓度药代动力学连续模型为两房室及三房室模型,而通常组织硼浓度是通过血硼浓度和静态组织与血液硼浓度之比的乘积作为实际组织硼浓度的代替物来建模的[21]。本文模拟含肿瘤(胶质肿瘤)Snyder模型,选取BPA-F介导的多形性胶质母细胞瘤BNCT情况进行分析研究,图8为硼药(BPA-F)静脉注射后颅内血液中10B的开放式二房室模型。
其中:中央室(central compartment)代表血液和注射分布良好的组织;周边室(peripheral compartment)代表注射较差的组织,如大脑;I为药物BPA-F注射的速率,mg·kg-1·min-1;C1,C2分别为各室的10B浓度;V1,V2分别为各室的分布容积;K12,K21,K10为速率常数,min-1。
结合二室模型,并以哈佛-麻省理工学院I期临床试验患者的药代动力学研究数据[22]做相应推导,得到中央室血硼浓度C1随时间的变化关系,如图9所示。根据图9,在BPA-F介导的多形性胶质母细胞瘤BNCT中,肿瘤与血液的硼浓度之比通常假定为3.5∶1,脑部与血液的硼浓度之比假定为1∶1,头皮与血液的硼浓度之比假定为1.5∶1,从而利用血硼浓度变化曲线来预测其他组织中的硼浓度变化[22]。本文选取上述曲线硼浓度上升阶段5个时间点,下降阶段10个时间点,共15个时间点,结合各组织倍数关系,利用Magic计算10B药代动力学模型下肿瘤的总相对生物效应剂量率随时间的变化关系,如图10所示。
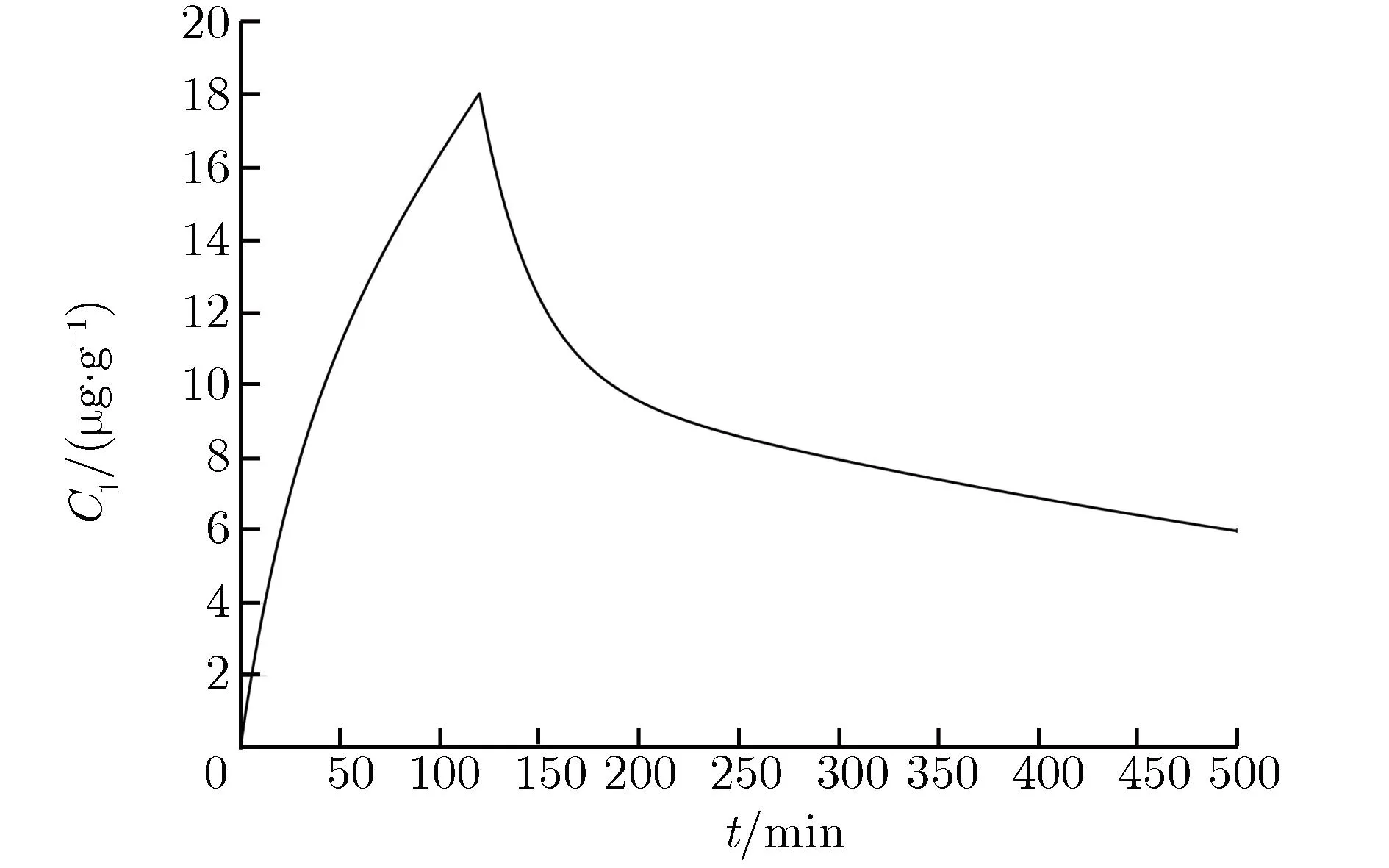
图9 中央室血硼浓度随时间的变化关系
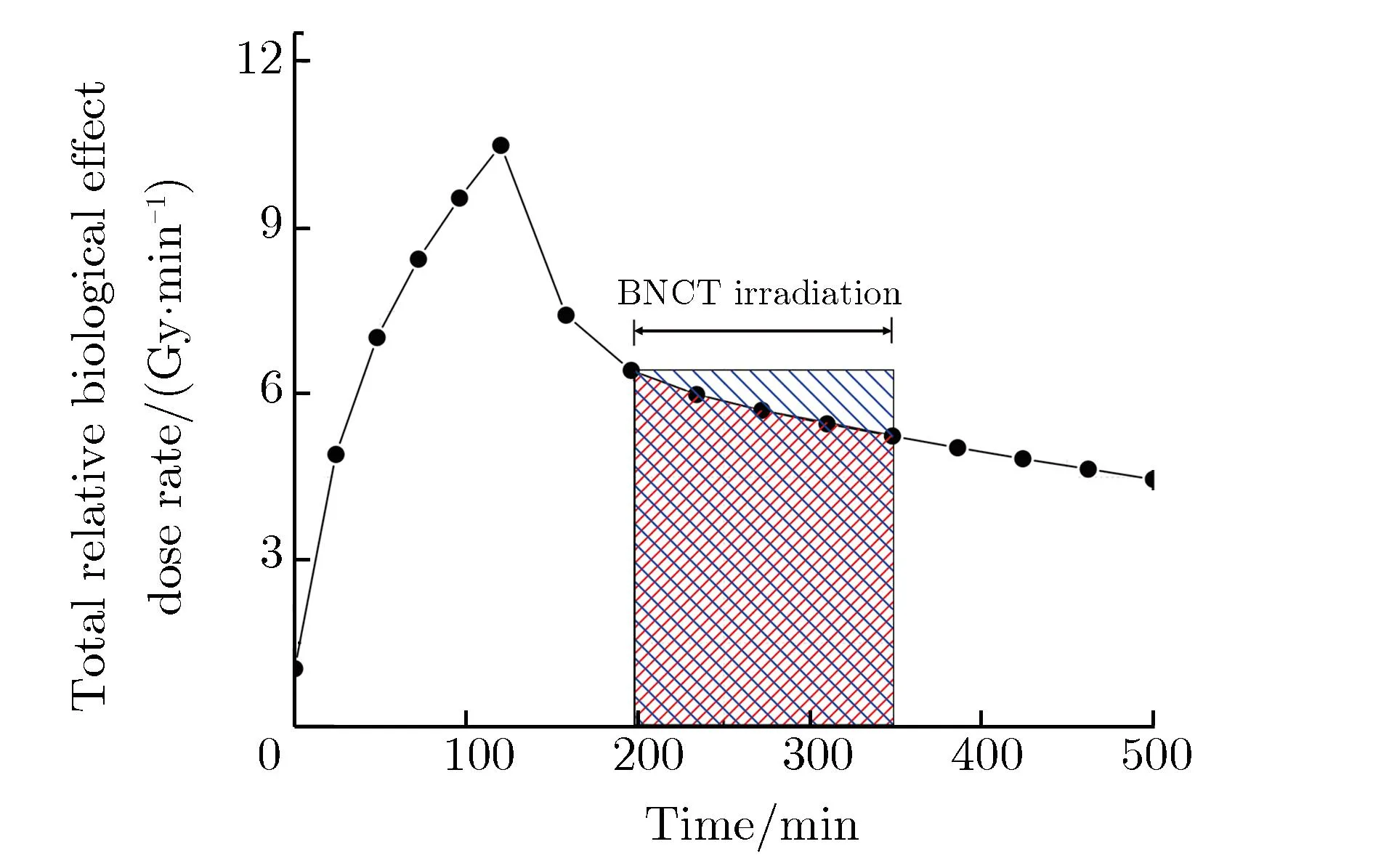
图10 10B药代动力学模型下肿瘤的总相对生物效应剂量率随时间的变化关系
图10中阴影部分的时间段,可视为BNCT治疗时持续照射的时间,红色阴影部分为建立了10B的药代动力学模型,考虑动态硼浓度变化后实际所受的剂量;蓝色阴影处为目前理论BNCT稳态下硼浓度所受的剂量。由图10可直观比较出二者的差异,对阴影面积(剂量值)进行偏差分析,二者阴影区域相对偏差为11.78%。因此,在BNCT临床治疗过程中,若不考虑患者体内硼浓度的动态变化过程,则可能导致实际受照剂量与处方剂量存在较大偏差,影响治疗效果。
4 结论
本文基于自主开发的BNCT蒙卡剂量计算程序Magic对国际Snyder修正模型进行剂量计算分析,通过MCNP得到深度-剂量率结果为标准进行对比,得出Magic程序计算的结果与参考文献结果相符,硼剂量率、热中子剂量率、超热中子及快中子剂量率、次级光子剂量率和总的相对生物效应剂量率的相对偏差均小于5%,满足临床治疗对计算精度的要求,验证了Magic程序正确性,同时证明Magic程序具有构建毫米量级千万网格数模型的承载力。基于Magic建立10B的开放式二房室药代动力学模型,对动态硼浓度下BNCT剂量学进行定量研究,根据血硼浓度变化曲线及各组织倍数关系,计算得出不同时间点下各硼浓度的肿瘤随时间变化的总相对生物效应剂量率变化拟合曲线。选取BNCT持续照射时间下,考虑动态硼浓度变化后,实际的所受的真剂量值及稳态下的硼浓度所受的假剂量值,计算得出二者的相对偏差为11.78%,可为临床更加准确的剂量计算及下一步完善含时蒙特卡罗剂量计算程序Magic提供参考。
