数十厘米长间隙真空绝缘研究进展
2023-03-11苏建仓
赵 亮,苏建仓,李 锐
(先进高功率微波技术重点实验室;西北核技术研究所:西安710024)
真空击穿是指当电压升高到一定程度时,两个电极间产生火花,并伴有较大的电弧电流通过的现象[1]。理想情况下,真空的绝缘性能仅受到电极表面场致发射的限制,理论上的耐压强度可达10 MV·cm-1,但实际上当电场强度达到100 kV·cm-1时就会发生电击穿现象。真空绝缘是脉冲功率领域中常见的绝缘形式之一,因易获取及成本低等特点而备受青睐。同时,高功率真空电子器件,如相对论返波管、相对论速调管、相对论磁控管、磁绝缘线振荡器及虚阴极振荡器等的迅猛发展[2],也是推动真空绝缘研究发展的重要原因之一。
描述真空击穿的机理主要有场致发射击穿理论、微放电击穿理论及微粒碰撞击穿理论3种。场致发射击穿是指强电场作用下发射电子导致的击穿,分为阴极微凸引起的击穿和阳极引起的击穿[1]。微放电击穿理论又称粒子交换理论(ABCD理论)[3],是指电极表面发射出一次电子、正离子和光子引起的击穿。微粒碰撞击穿理论指电极系统中因微粒碰撞产生金属蒸气而导致的击穿。近年来,研究人员在场致发射击穿理论的基础上又提出了爆炸发射理论[4]。上述理论对于进一步认识真空击穿的机制起到促进作用。
1995年, Latham[5]详述了上述真空击穿机制,同时,还对影响真空绝缘的因素进行了综述,从电极角度来看,这些因素包括电极材料、表面光洁度、几何形状、烘烤处理及介质表面是否覆膜等;从真空角度,包括真空度、真空间隙g及环境温度等;同时电压波形也会对真空击穿阈值产生影响。上述因素的影响多是针对数毫米短间隙条件下的真空击穿现象,对长间隙下真空绝缘击穿现象关注不够充分。鉴于此,本文简要梳理长间隙下的真空击穿研究结果。
1952年,Cranberg等[6]总结了间隙为0.1 mm~10 m时真空击穿电压Ub,并将其绘制在双对数坐标下,发现,Ub随真空间隙近似成线性关系,斜率近似为0.5;从能量角度提出了粒子碰撞理论来解释长间隙真空击穿,且从理论上得出了Ub∝g0.5的关系,这是首次对长间隙真空击穿较系统的总结。
1957年,Slivkov等[7]引入了两个约束条件,使Cranberg的理论更加符合物理实际。首先,假设微粒需具备足够的能量才能在撞击时被全部汽化;其次,认为微粒撞击须产生足够的蒸气才可能引发击穿;通过这两个假设,发现微粒半径既不能太大,也不能太小,且得到了Ub∝g0.625的关系。
1962年,Farrall等[8]基于Cranberg的粒子假设,引入了脉冲作用时间,并通过理论求解粒子运动方程,发现闪电脉冲存在Ub∝g5/6的关系。1985年,Farrall[9]对之前相关的真空击穿机理进行了较为全面的综述,总结了包括场致发射、阳极因素、金属杂质、间隙效应及污染物等因素对真空绝缘的影响。
1997年,Spolaore等[10]再次总结了间隙为0.1 mm~10 m时的真空击穿电压随间隙变化的实验数据,发现在Ub=Cgα关系中,α并非常数,而是随着真空间隙增大逐渐从1减小至0.5。这个实验结果与Cranberg等[6]的结果相悖。
2011年,Pilan等[11]从Weibull概率角度给出了一个Ub随g变化的理论公式,表示为
(1)
其中:Cp为常数;m为Weibull分布的形状参数;χ为几何形状。根据式(1),若m取值为7.3~30,对应g的指数为0.52~0.6。
2011年,西安交通大学的Zhang等[12-13]通过实验研究了间隙为1~5 cm时真空断路器的绝缘特性,同样得到了Ub∝gα的关系,α的取值为0.70~0.79;同时,从理论上给出Ub随g变化的关系,α的理论值为0.76。
从2012年开始,西北核技术研究所的研究人员[14-16]结合脉冲功率装置的研制需求,对微秒脉冲下同轴真空电极和平板电极的真空绝缘特性进行了较全面的研究,真空间隙为1~10 cm,得到了一些经验公式和基本认识。本文主要对同轴电极下的长间隙真空绝缘特性、平板电极下的长间隙真空绝缘特性、长间隙真空绝缘机理及真空绝缘提高措施等方面内容进行综述。
1 同轴电极真空绝缘阈值经验公式
1.1 实验平台
基于1台TPG400微秒脉冲发生器[17],对同轴真空电极下的长间隙绝缘特性展开了研究。图1为用于真空绝缘研究的TPG400实验平台。
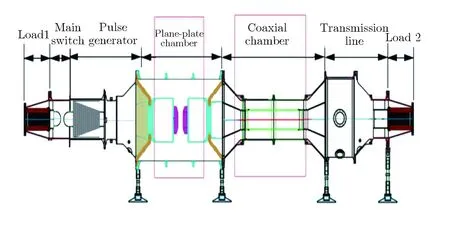
图1 用于真空绝缘研究的TPG400实验平台
TPG400是1台Tesla型脉冲发生器,可输出微秒双极性波形,第一峰极性为负,半高宽为30 μs,最大幅值为800 kV。实验时控制击穿发生在第一峰,真空击穿和不击穿时的波形对比如图2所示。

图2 真空击穿和不击穿时的波形对比[16]
TPG400是1台多功能实验平台,输出脉冲的脉冲宽度及极性等参数可调,且实验电极可调,如,在连通平板电极实验腔体的两个电极后,TPG400可用于测试同轴电极的绝缘特性;反之,在保证同轴电极绝缘余量足够的前提下,通过调节平板电极的间距,TPG400可用于测试平板电极的真空绝缘特性。测试过程中,真空度维持在(1~5)×10-3Pa。
1.2 测试结果及经验公式
首先令两个平板电极直接相连,完成了3组同轴电极下的真空绝缘实验,TPG400及文献中的同轴电极参数和击穿电压测试结果如表 1所列。其中:Ro为同轴电极外半径;Ri为同轴电极内半径;L为同轴电极长度;A为内电极有效面积;kgA为常数。
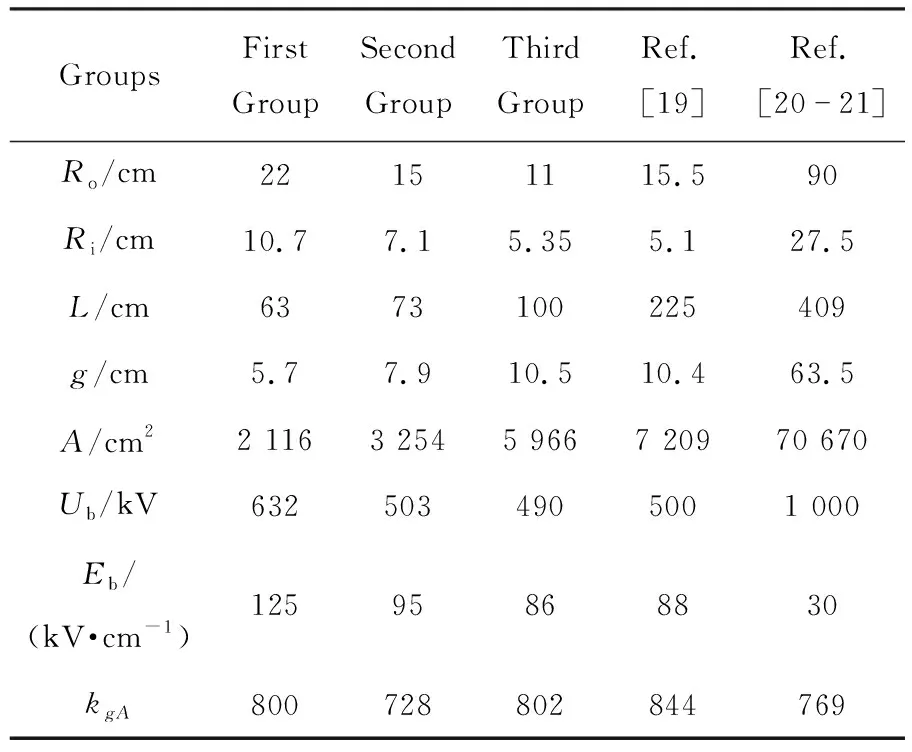
表1 TPG400及文献中的同轴电极参数和击穿电压测试结果[18]
表1还列出了文献[19-21]与同轴电极相关的实验数据。同轴线电场强度可表示为
(2)
根据式(1),可计算相应的击穿电场。下面将结合这些基础实验数据,总结出与同轴电极绝缘相关的经验公式。首先假设真空击穿电场Eb随间隙g和面积A的变化关系可表示为
(3)
考虑到Slivkov等[7]总结的总电压效应,击穿电压可表示为
Ub(g)=Cgγ
(4)
其中:C为常数;γ约为0.625。认为电场均匀,则
(5)
由式(3)和式(4)可知,α≈1/3。令α=1/3,以Ebg1/3为函数,以A为自变量,对TPG400实验数据的拟合如图3所示。由图3可得β≈1/6。所以,用于描述同轴电极下长间隙真空绝缘阈值的经验公式可表示为
(6)
根据式(5),对TPG400及文献[16]的长间隙同轴电极真空实验结果进行拟合,如图4所示。由图4可见,β≈1/6的结论仍然成立,验证了式(6)的正确性。由图4还可见,式(6)的适用范围为:g<63.5 cm;A<70 000 cm2。
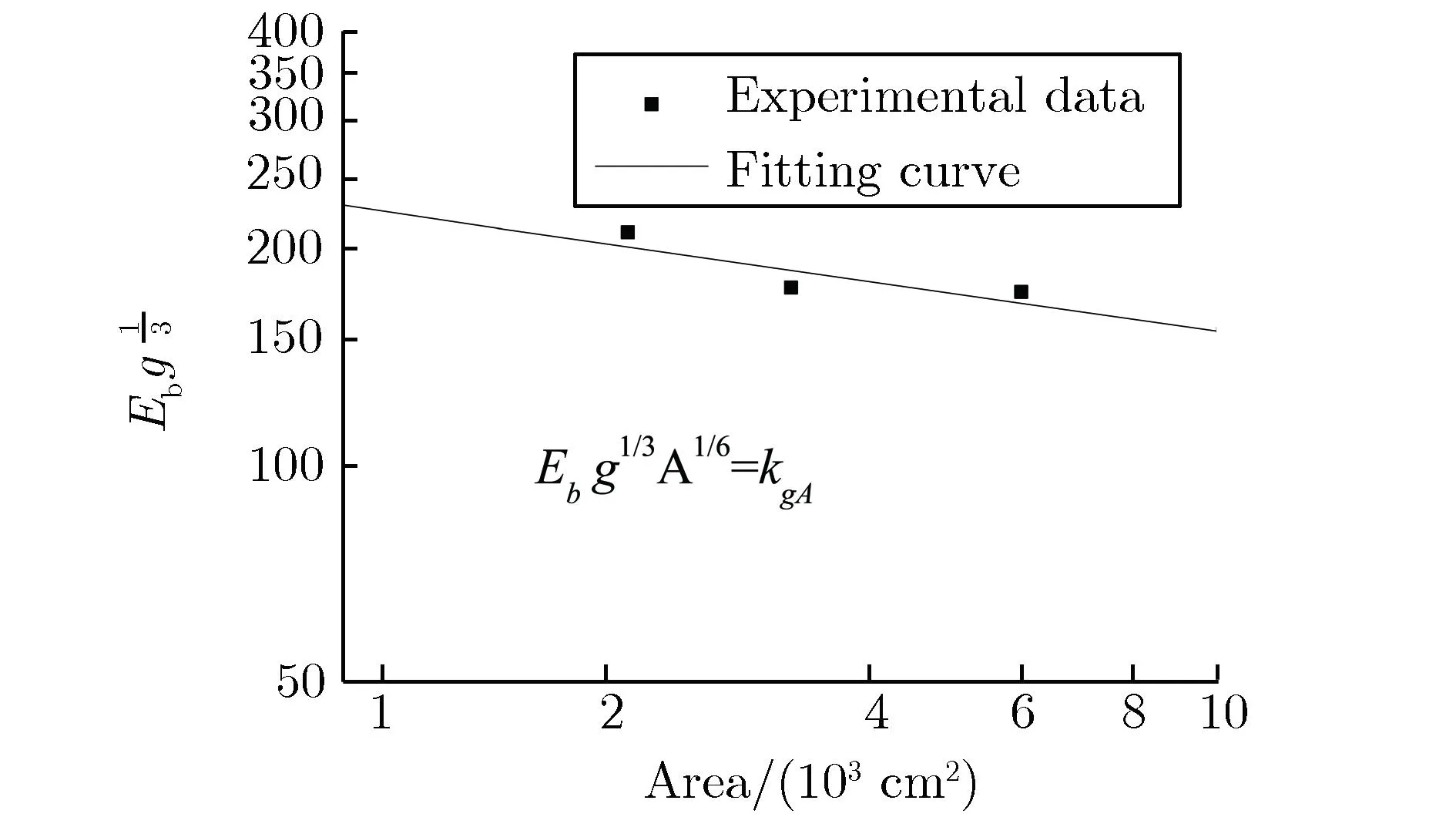
图3 对TPG400实验数据的拟合[16]
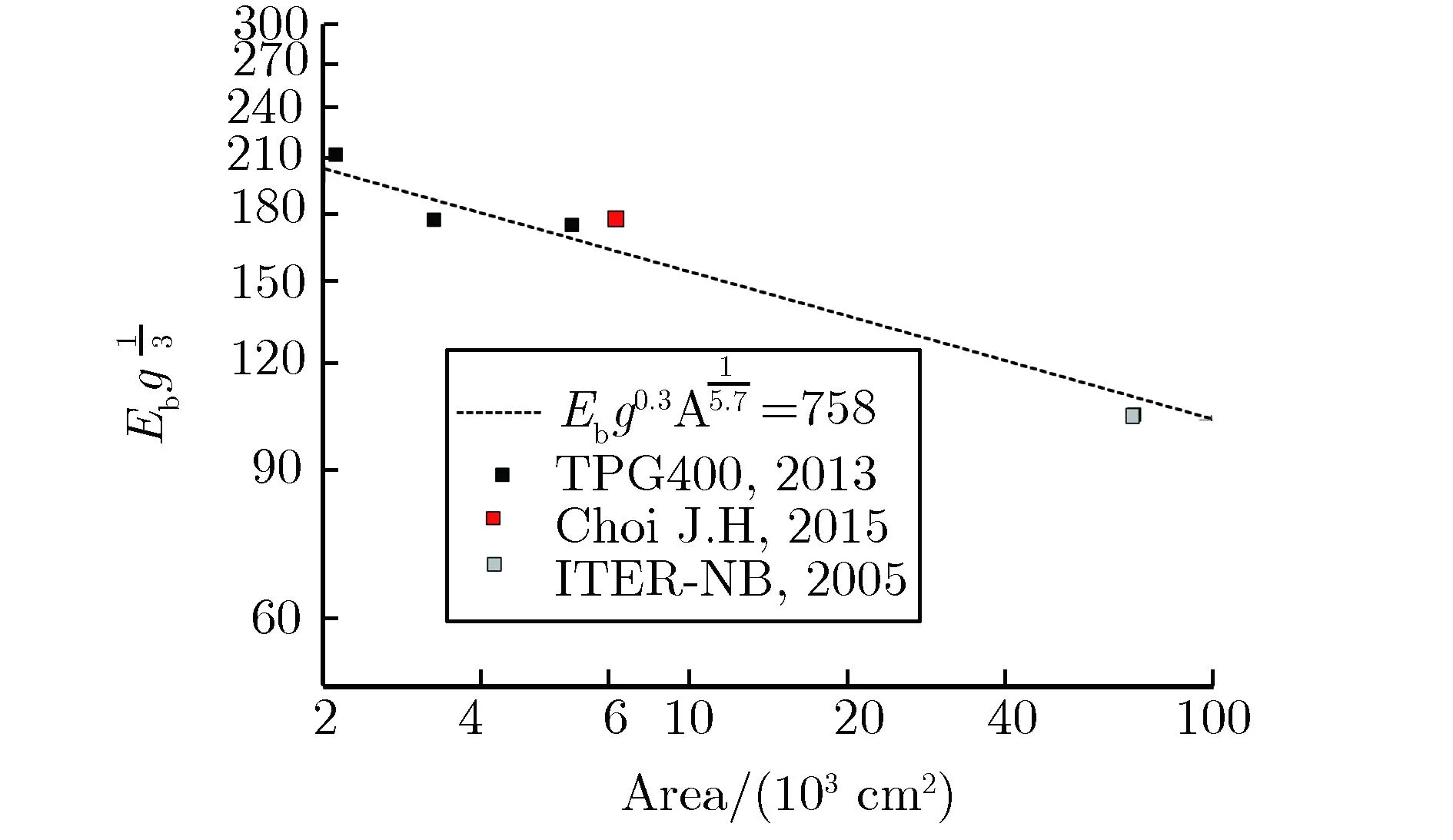
图4 对TPG400及文献[16]的长间隙同轴电极真空实验结果的拟合
2 平板电极真空绝缘阈值经验公式
对于TPG400实验平台,如第1节所述,令同轴实验腔体留够绝缘余量,并令平板实验腔体的两个电极分开,便可开展平板电极真空绝缘实验。完成了2.5~5.5 cm间隙下的平板电极真空绝缘实验,电极外形为布鲁斯状(Bruce shape),可实现电场增强因子1.03~1.05的准均匀电场。电极直径为11 cm,材料为不锈钢(304C)及硅钢(DG6)等材料,图5为长间隙平板电极真空实验中用到的电极。图6为TPG400实验平台击穿电压随间隙变化关系实验结果的拟合。

图5 长间隙平板电极真空实验中用到的电极
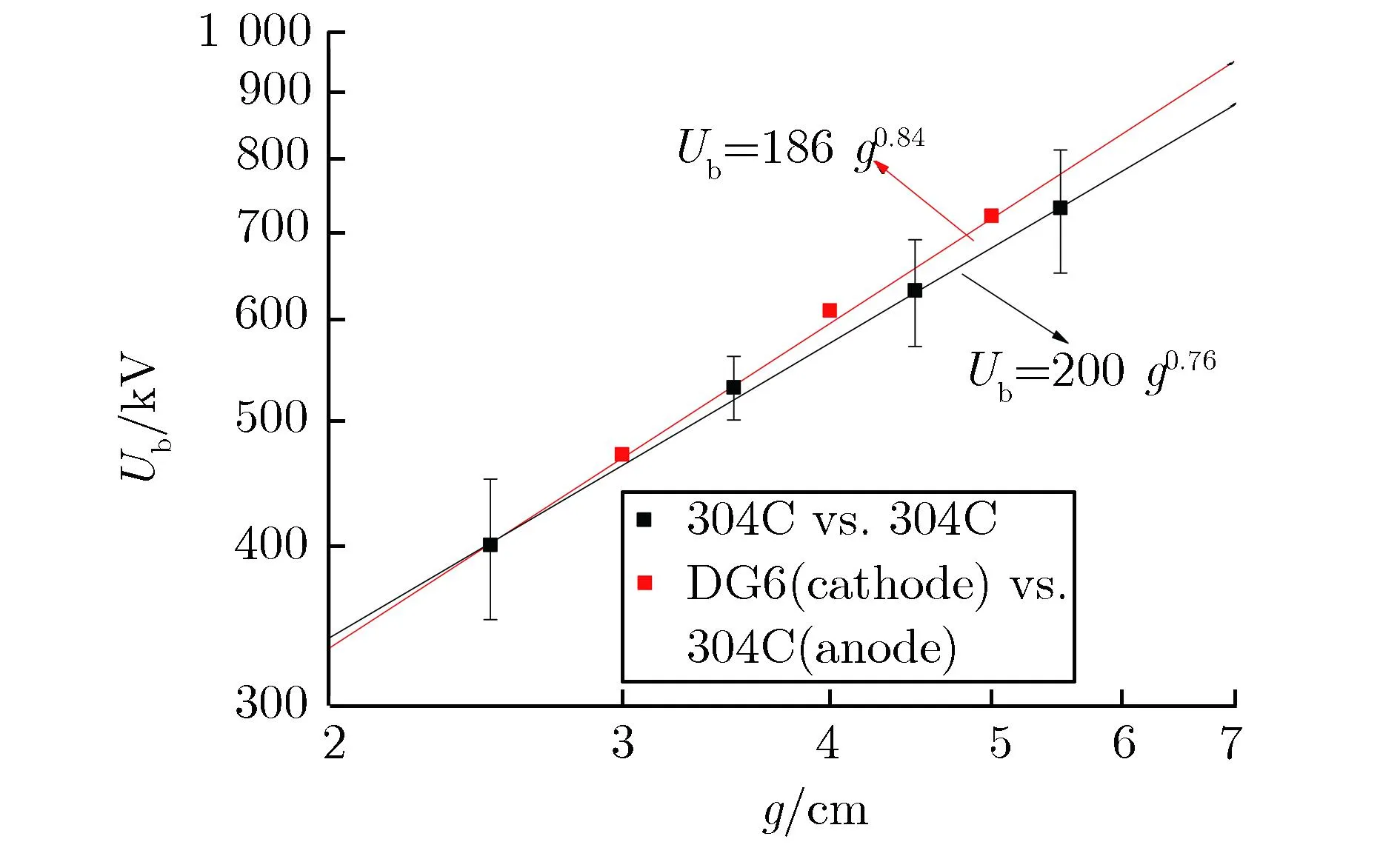
图6 TPG400实验平台击穿电压随间隙变化关系实验结果的拟合
由图6可见在双对数坐标系下,Ub随g的变化关系基本满足线性关系,但γ为0.76~0.84,大于Slikov得出的结论0.625。为此,将文献中与长间隙平板电极真空绝缘相关的实验结果与本文实验结果共同绘制于同一坐标系,图7为文献[15]击穿电压随间隙变化关系实验结果的拟合。
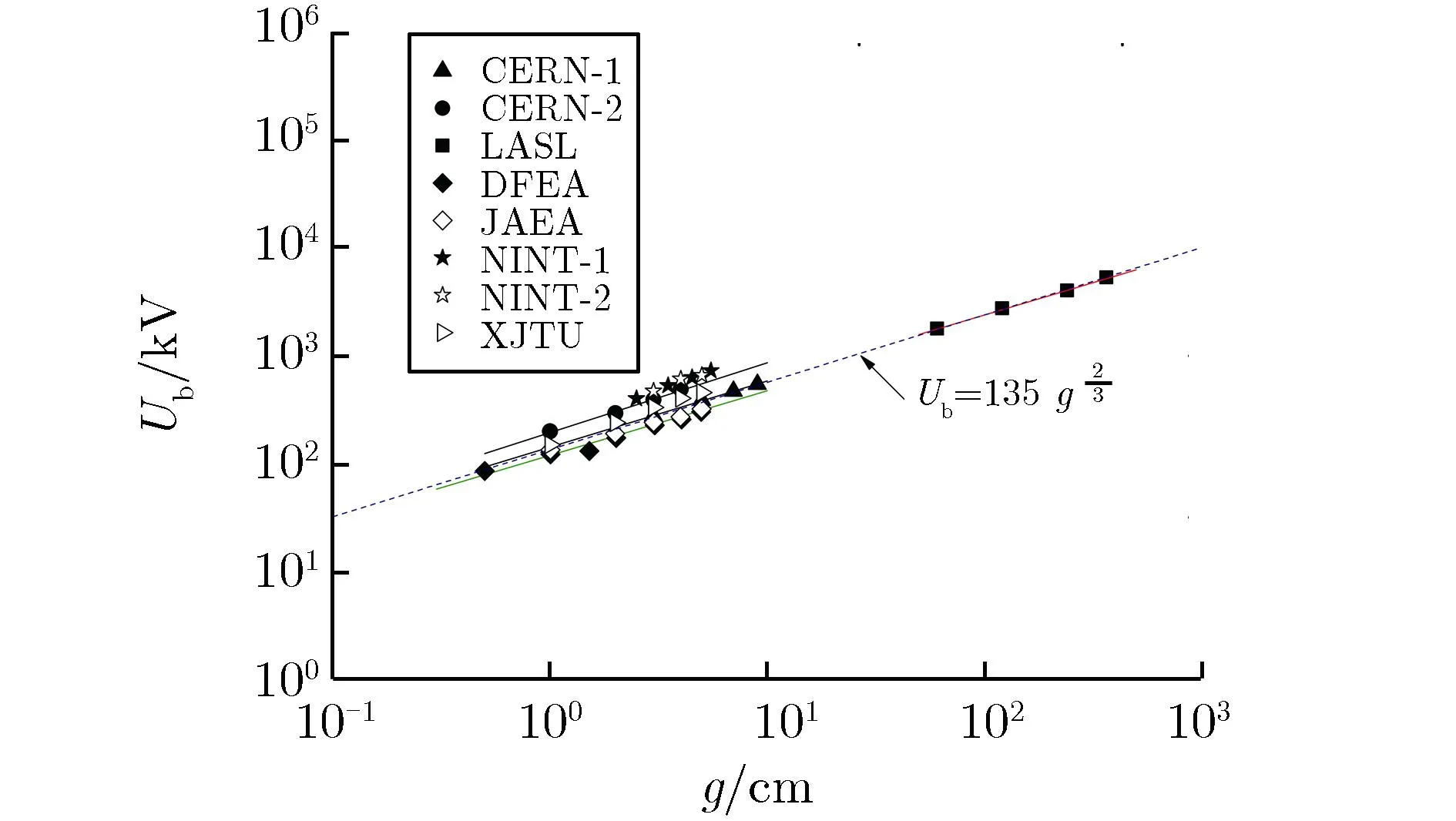
图7 文献[15]击穿电压随间隙变化关系实验结果的拟合
由图7可见,γ取值约为0.667。进一步,假设所有实验结果均在均匀电场下获得,便可在双对数坐标系下拟合Eb随间隙g的变化趋势,图8为文献[14]击穿电场强度随间隙变化关系实验结果的拟合[14]。由图8可见,Eb随g的变化关系可表示为
(7)
其中:间隙g的范围为4 mm~4 m。值得说明的是,这一结果与描述同轴电极真空绝缘的经验公式式(6)的内涵一致。
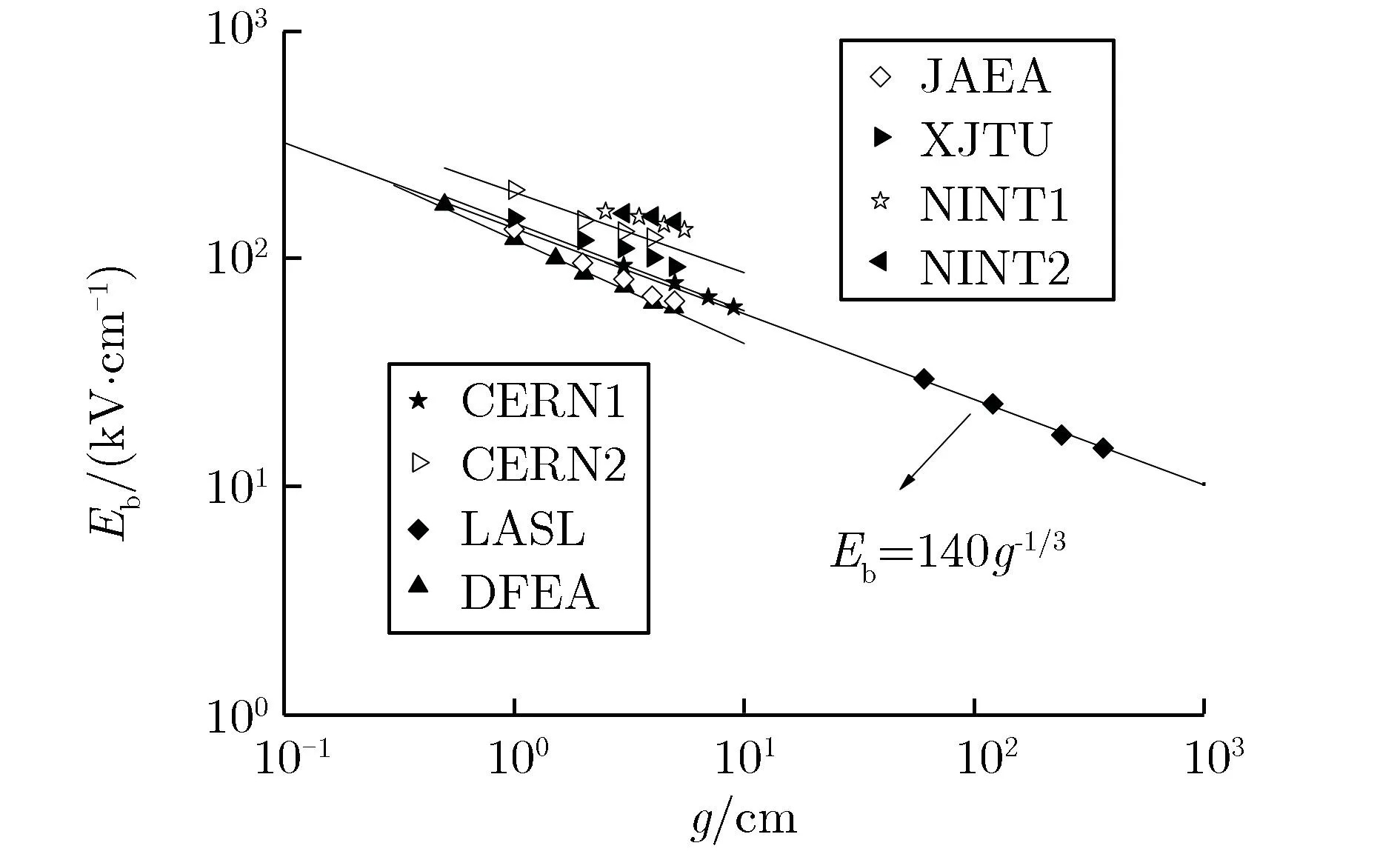
图8 文献[14]中击穿电场强度随间隙变化关系实验结果的拟合
3 微秒范围真空绝缘阈值经验公式
TPG400的脉冲宽度不可调,因此只获得脉冲宽度τ为30 μs时的真空击穿电场强度。为进一步研究长间隙真空击穿电场强度随脉冲宽度的变化,本文总结了西北核技术研究所及相关文献中提到的不同脉冲宽度下与真空绝缘相关的实验数据,其中,电子管的实验数据来自文献[5];石墨电极和铅电极数据来自文献[22]。设Eb随τ同样满足负指数幂关系,即Eb(τ)=Cτg-δ,在双对数坐标系下对上述实验数据进行了拟合,图9为真空击穿电场强度随脉冲宽度的变化关系。由图9可得
(8)
注意,式(7)的成立范围为1 ns≤τ≤1 ms。当τ>1 ms时,Eb随τ的变化不明显。再考虑到真空击穿阈值随电极间隙和面积变化的经验公式及A,g,τ3个参数相互独立,则可得到关于Eb的经验公式,可表示为
(9)
其中,K为常数。

图9 真空击穿电场强度随脉冲宽度的变化关系
4 长间隙真空击穿物理机制
如第2节所述,真空击穿现象的机理包括阴极微凸诱发场致发射理论、阳极蒸气诱发场致发射理论、微放电击穿理论、微粒碰撞击穿理论和爆炸发射理论。对于长间隙真空击穿现象,学术界普遍认可的机制为微粒碰撞击穿理论。该理论最早由Cranberg[6]提出后经Slivkov修正[7],他们认为,电极系统中往往存在一些微粒,它们可疏松地黏附于电极表面或从外部飞入两个电极之间;在静电场作用下,这些微粒感应带电,并被静电场拉过间隙,以足够高的能量轰击相反极性的电极;微粒与电极碰撞后,动能转变为热能,使微粒本身或者电极局部区域熔化和蒸发,释放出蒸气,引起电离。微粒碰撞击穿理论的要点包括:微粒从一个电极飞向对面电极、微粒碰撞导致局部电极材料蒸发或微粒自身蒸发、金属蒸气被电离形成等离子体及击穿电压与间隙满足总电压效应,即Ub=Cg0.625。结合这些要点,分析长间隙真空击穿结果与现象:
(1)对于本文总结的长间隙真空绝缘阈值经验公式,无论是式(6)还是式(7),都反映出Ub=Cg2/3,这与微粒理论的第4点中γ=0.625的结论基本相符。
(2)当采用一对布鲁斯电极且阴极为TC4,阳极为不锈钢时,在TC电极表面发现了不锈钢的溅射点,图10为TC4电极表面出现的不锈钢溅射斑点[15]。
(3)当完成一对不锈钢平板电极真空实验时,其中,两个不锈钢电极表面均匀涂有聚酰亚胺(PI)涂层包覆,以期望提高真空绝缘阈值。而实验结果恰恰相反,PI涂层并未提高Ub,反而使Ub降低了27%,图11为不锈钢电极表面有PI包覆和无PI包覆的击穿电压对比。根据实验结果推测,PI涂层起到了空间微粒源的作用,有助于真空击穿发生,因此,击穿阈值降低。
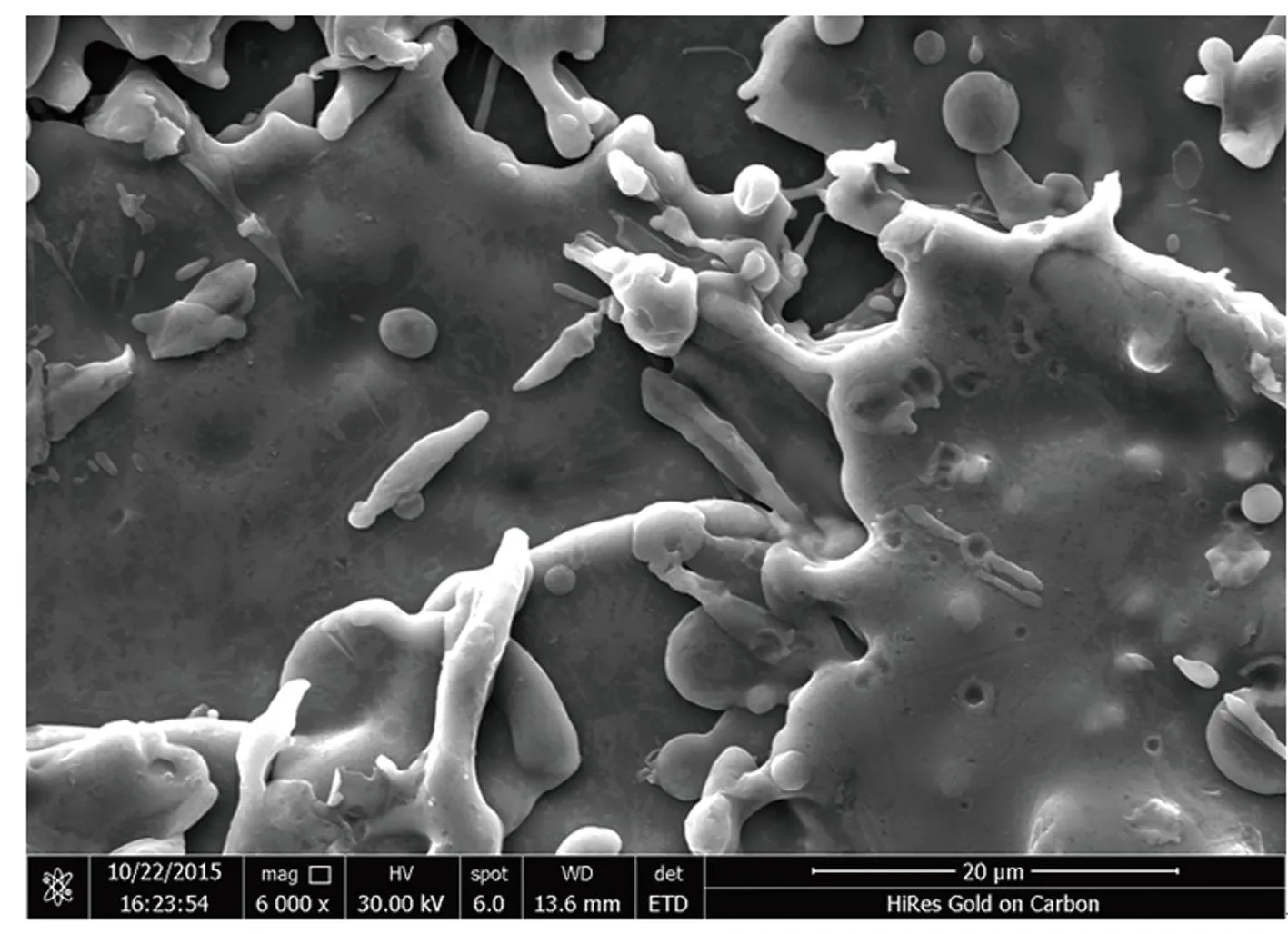
图10 TC4电极表面出现的不锈钢溅射斑点[15]
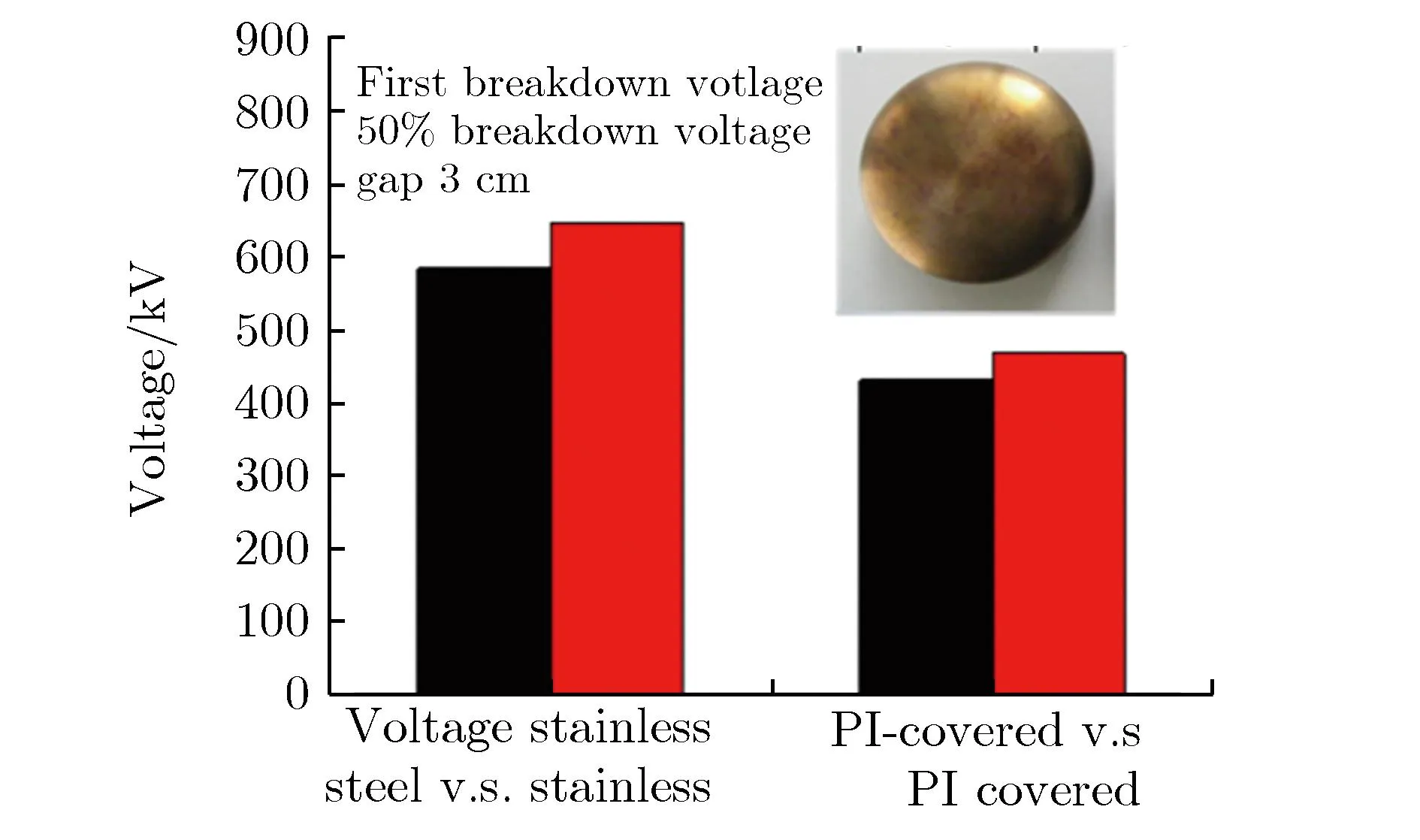
图11 不锈钢电极表面有PI包覆和无PI包覆时的击穿电压对比
5 真空绝缘阈值提高方法
平板电极的实验结果显示,对较均匀的布鲁斯电极,平均击穿电场强度为150~200 kV·cm-1。实际应用中,希望这个真空绝缘水平能再提高。文献中报道的可提高真空击穿阈值的方法包括抛光、老炼、高温除气及表面加半导体涂层等[1]。考虑到可行性和方便程度,综合选取抛光方法和老炼方法开展研究。
5.1 粗糙度对真空绝缘阈值的影响
以TC4电极为实验对象,首先研究了粗糙度对真空绝缘阈值的影响,实验中选取了3个粗糙度Ra水平:粗车水平,Ra=1.1 mm;一般水平,Ra=0.08 mm;精抛水平,Ra=0.06 mm。图12为TC4电极真空击穿电压随粗糙度的变化关系。由图12可见,电极表面粗糙度越低(或光洁度越高),真空绝缘阈值越高。

图12 TC4电极真空击穿电压随粗糙度的变化关系
考虑到获得较低粗糙度(0.06 mm)付出的代价较大,且难于在大面积、形状复杂的电极上应用,综合考虑实际中采用0.08 mm的粗糙度水平较为适合。0.08 mm的粗糙度获得方式有手抛和研磨2种,前者适合表面小但不规则的电极,后者适合表面大但较为规则的电极。实际应用中须结合具体情况选择抛光方式。
5.2 老炼对真空绝缘阈值的影响
适当的老炼会去除电极表面的“毛刺”和沾染杂质,进而能提高真空绝缘水平,但问题是如何控制老炼的度。为此,本文对不同的电极,采用逐级升压法,控制升压的步长,在每个电压等级下老炼若干炮。发现,随着电压升高,会出现“微放电”、“首次击穿”及“50%击穿”3种放电等级。图13为不同放电情况下的电压水平。
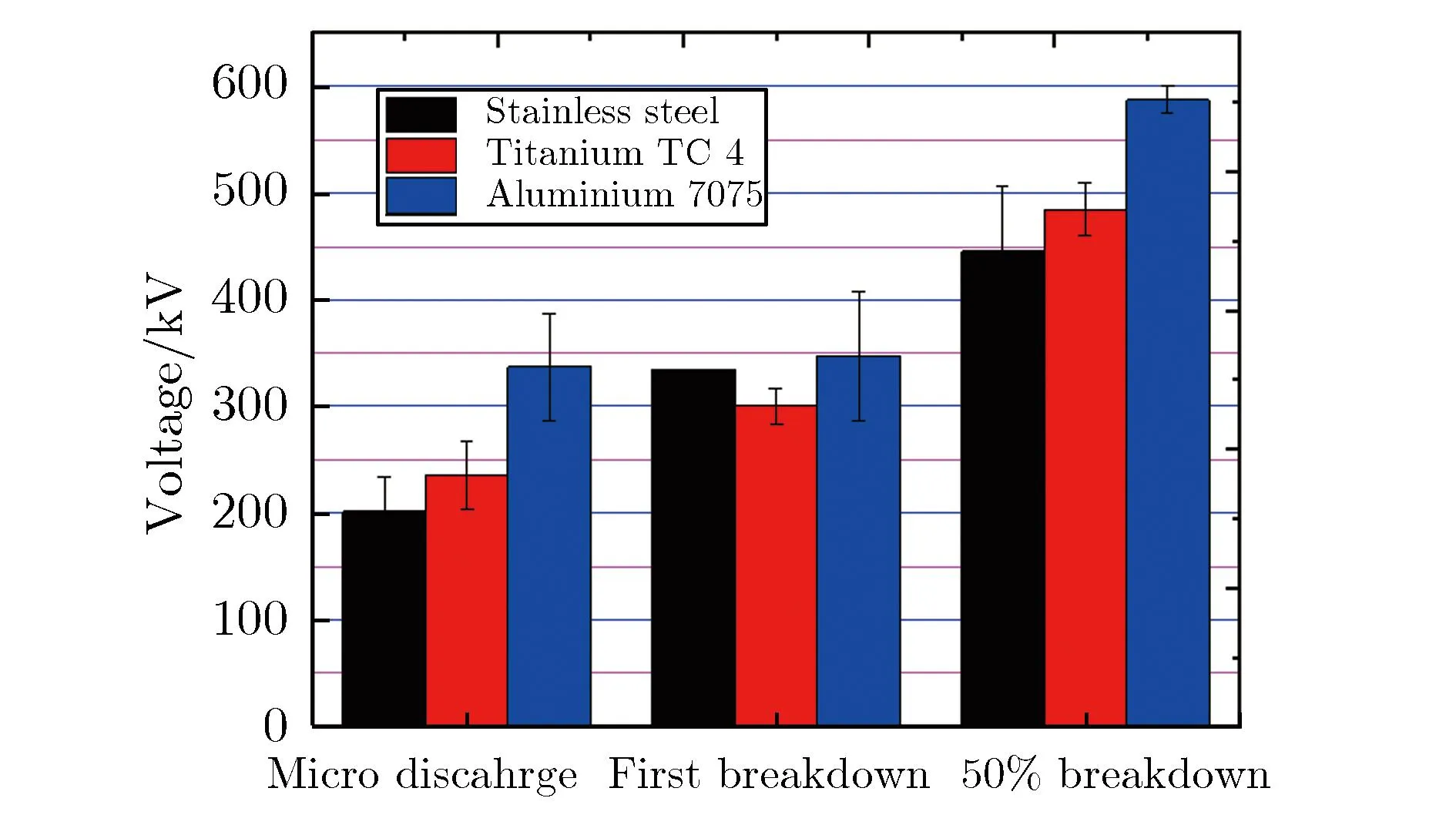
图13 不同放电情况下的电压水平
当电压UA超过首次击穿电压UF,则真空绝缘将难以维持;反之如控制UA小于首次击穿电压,则可得到一个高于微放电压UM且可靠工作的电压等级。定义此电压为老炼电压,表示为
UM (10) 老炼可提高实际真空绝缘水平。 本文综述了西北核技术研究所在微秒长间隙真空绝缘领域的研究进展,主要结论为 (1)对于长间隙真空绝缘,击穿阈值Eb与真空间隙g、电极面积A和脉冲宽度τ之间的关系为:K=Ebg1/3A1/6τ1/6,其中, 4 mm (2)微粒碰撞击穿理论比其他理论更适合解释长间隙下的真空绝缘现象; (3)实际应用中提高真空绝缘水平的简便易行的方法有表面抛光和老炼;效费比较高的抛光水平为粗糙度取0.08 mm;老炼电压应大于微放电电压,但小于首次击穿电压。6 小结
