裂变燃耗计算中裂变产额数据的适用性评估
2023-03-11师全林王立鹏余功硕梁建峰姜文刚张小林
师全林,王立鹏,余功硕,梁建峰,姜文刚,解 峰,张小林
(西北核技术研究所,西安710024)
通过裂变核的消失量或裂变过程中裂变产物的生成量均可计算出核材料的裂变燃耗。用裂变产物的生成量计算裂变燃耗时要用到裂变产额数据,通常采用实验室测量数据的评价结果。实验室测定裂变产额时,中子注量率一般不超过1014cm-2·s-1,而核爆炸时中子注量率可能超过1030cm-2·s-1,实验室测定的产额数据能否适用于超高中子注量率下裂变燃耗的计算一直是广为关注的问题之一。钱晶等[1]研究建立了考虑中子参加反应的裂变产物中子反应及衰变的网络方程,考察了热中子诱发235U裂变时裂变产物核随时间的变化关系,指出是否考虑中子与裂变产物的核反应对裂变产物核的数量随时间的变化关系影响显著,在该文献的计算条件下147Nd累积产额的变化达到了13%。冯晶等[2-3]建立了一个简化的强中子场模型,计算了(n, γ) 和(n, 2n)反应引起链产额的变化,认为链产额的相对变化率并不显著。
本文探讨了不同中子注量率和裂变燃耗深度下两种方法计算的裂变燃耗结果的差异及原因,评价裂变产额数据的适用性。
1 裂变燃耗的两种计算方法
1.1 通过裂变核的消失量来计算裂变燃耗
裂变核在中子场的作用下会发生裂变和俘获等多种中子核反应,核子数N随时间变化关系的微分方程可表示为
(1)
其中:φ为中子注量率;σa为表观消失截面,是指裂变核通过裂变、俘获及2n等中子核反应“消失”和“产生”的总截面,与各核反应的截面和核材料的同位素组成等因素相关。如对于235U,表观消失截面与其裂变、俘获、2n等中子核反应截面、234U的(n, γ)截面及236U的(n, 2n)截面等相关,可近似表示为
(2)
若中子注量率φ为常数,则式(1)的解为
N=N0·e-φ·σa·t
(3)
其中,N0为裂变核的初始核子数。t时刻发生裂变的核子数Nf可表示为
(4)
考虑到Nf(t=0)=0的边界条件,式(4)的解为
(5)
裂变燃耗x定义为发生裂变反应的核数与裂变核初始总数的比,表示为
(6)
由式(6)可知,裂变燃耗与中子注量率、裂变核的表观消失截面与裂变截面及中子作用时间相关,最大值为σf/σa,通常小于1。如热中子作用下的235U,其裂变截面和俘获截面分别为585 b和98.7 b,若表观消失截面主要为裂变截面和俘获截面之和,则235U裂变燃耗的最大值为0.86。当裂变燃耗小于最大值时,裂变燃耗取决于中子注量率和中子作用时间的乘积,中子作用时间与裂变燃耗之间的关系可表示为
(7)
裂变核的消失量可通过测定中子作用前后核材料同位素含量的变化获得。利用式(6)计算裂变燃耗时,截面的不确定度直接影响裂变燃耗的准确性,特别是中子能谱较复杂时,谱平均截面不易准确计算。但某些裂变产物的产额对中子能谱的变化不敏感,用裂变产物的生成量来计算裂变燃耗时可减小中子能谱变化带来的不确定度。
1.2 通过裂变产物的生成量来计算裂变燃耗
裂变核在中子场作用下生成裂变产物i,核子数的变化主要考虑通过裂变核反应按其产额生成、衰变消失及中子核反应消失3个方面。裂变产物i通过中子核反应消失的截面也用表观消失截面σa, i来表示,它主要与该裂变产物的中子俘获截面、2n截面、与该裂变产物质量数相近的裂变产物数及其中子核反应截面相关。裂变产物i的核子数Ni可表示为
(8)
其中:λi为i的衰变常数;Yi为i的裂变产额。考虑到Ni(t=0)=0的边界条件,式(8)的解可表示为
(9)
若实验测定中子作用结束时刻裂变产物的核子数Ni后,可求得中子作用结束时刻的裂变数,表示为
(10)
根据裂变燃耗的定义可用裂变产物法求得燃耗,表示为
(11)
当σa>>λi/φ+σa,i且(λi+φ·σa,i)·t≈0时,式(11)与式(6)的结果是一致的,但若上述条件不满足,则两种方法的计算结果会出现差异。
2 中子注量率的影响评估
本文通过解析方程的计算来讨论不同中子注量率情况下两种方法计算的裂变燃耗,计算中裂变核的表观消失截面取1 b,该截面由裂变核的裂变截面和俘获截面构成,分别取0.8 b和0.2 b。
2.1 低中子注量率下的裂变燃耗
根据式(11),低中子注量率条件可认为是满足φ<<λi/σa,i的实验条件。对于半衰期为1 a的裂变产物,衰变常数为2.2×10-8s-1,若消失截面为1 b量级,则中子注量率小于1016cm-2·s-1时可认为是低中子注量率条件。通常实验室条件下,对半衰期小于数年的裂变产物而言,中子注量率小于1014cm-2·s-1时,可认为是低中子注量率条件。在该条件下,若裂变产物与裂变核的表观消失截面相当,则式(11)可近似表示为
(12)
由式(12)可知,裂变燃耗只与裂变产物的衰变常数和裂变核的表现消失截面、裂变截面等核数据相关。低中子注量率条件下不同方法计算的裂变燃耗随时间的变化关系如图1所示。由图1可见,当中子作用时间较短,裂变燃耗足够小时,用不同半衰期的裂变产物及其裂变产额计算的裂变燃耗与用核反应截面计算的裂变燃耗一致;但当中子作用时间足够长,裂变燃耗足够大时,用裂变产物产生量计算的裂变燃耗低于用裂变核消失量计算的裂变燃耗,且裂变产物的半衰期越长,产生偏差所需的中子作用时间越长。
上述差异的原因不难理解。低中子注量率条件下,燃耗较高时,再增大燃耗需很长时间。当中子作用时间远超过裂变产物的半衰期时,裂变产物的生成达到了饱和状态,数量不再增加,因此用与时间无关的裂变产额计算的裂变燃耗不再增大,导致两种方法计算的燃耗差异越来越大。
2.2 高中子注量率下的裂变燃耗
根据式(11),高中子注量率条件可认为是满足φ>>λi/σa,i的实验条件。当裂变产物的表观消失截面约为1 b且其半衰期为1 s时,中子注量率大于1024cm-2·s-1时可认为是高中子注量率条件。在1030cm-2·s-1高中子注量率条件下,对于半衰期大于1 s的裂变产物,与中子反应截面相比,λi/φ为可忽略的小量,则式(11)可近似表示为
(13)
显然式(13)计算的裂变燃耗与裂变产物的半衰期无关,主要取决于裂变核和裂变产物的表观消失截面。高中子注量率下不同方法计算的裂变燃耗随时间的变化关系如图2所示。
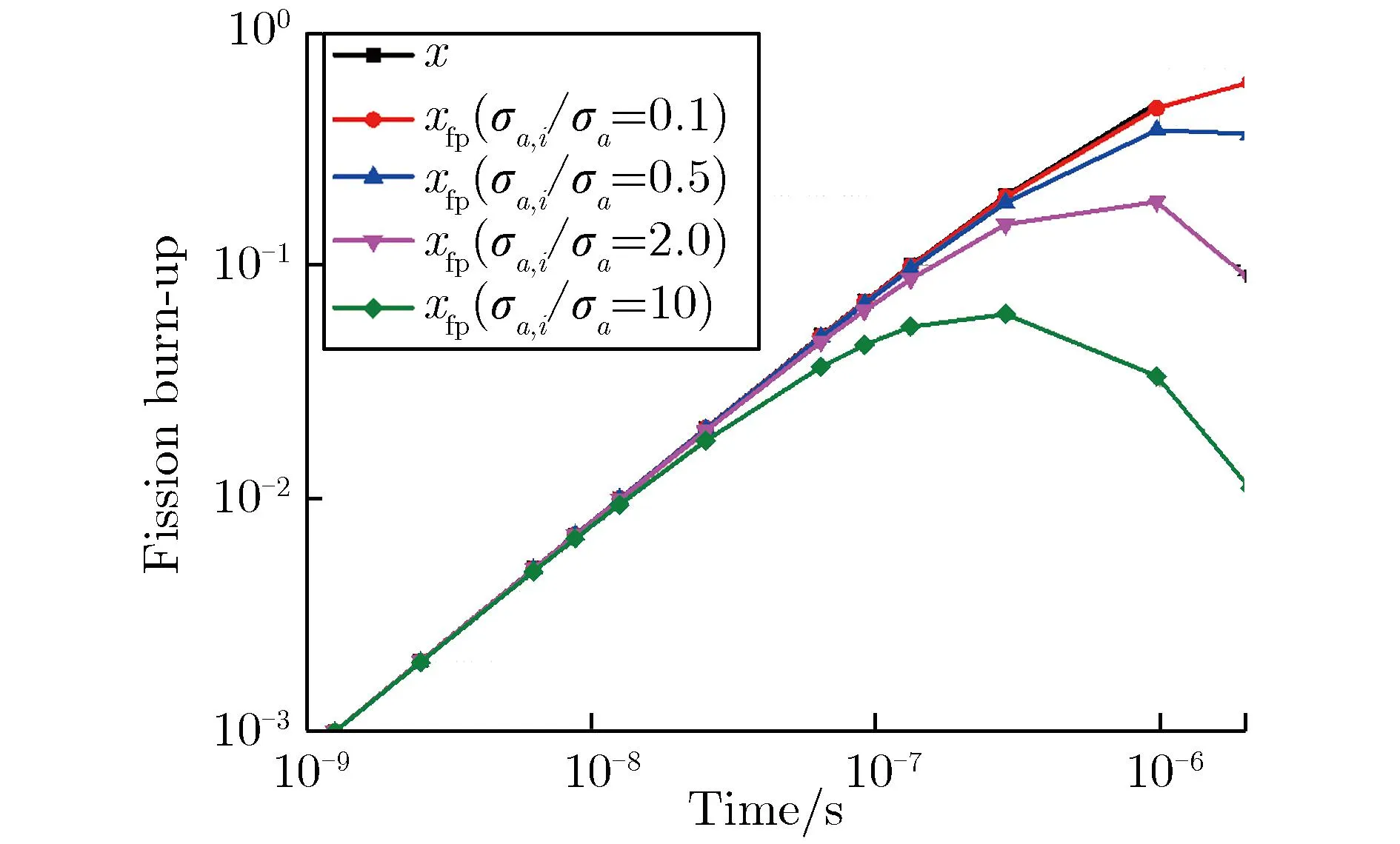
图2 高中子注量率下不同方法计算的裂变燃耗随时间的变化关系
由图2可见,当裂变产物的表观消失截面相对于裂变核越小,裂变燃耗的计算结果越一致。表1为不同消失截面下两种方法计算裂变燃耗的相对偏差。
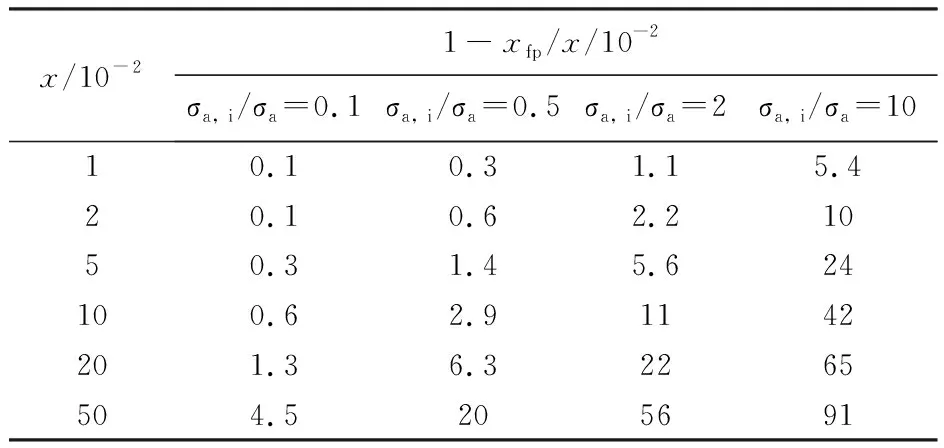
表1 不同消失截面下两种方法计算裂变燃耗的相对偏差(1- xfp /x)
由表1可知,裂变产物相对于裂变核的表观消失截面越小,裂变燃耗越低,两种方法计算的结果越一致;当裂变燃耗高于20%时,若裂变产物的消失截面比靶核消失截面的一半还要高时,则用裂变产物计算的裂变燃耗要低于6%以上,必须进行修正。
综上,无论中子注量率高低,只要裂变燃耗足够小,不同方法计算的裂变燃耗总是一致的。当裂变燃耗足够大时,用式(11)比用式(6)计算的裂变燃耗偏低,但偏低的原因不同,低中子注量率条件下,主要是由于短寿命裂变产物的生成量达到了饱和;高中子注量率条件下,主要是由于裂变产物通过中子核反应有一定量的“消失”。
3 模拟计算
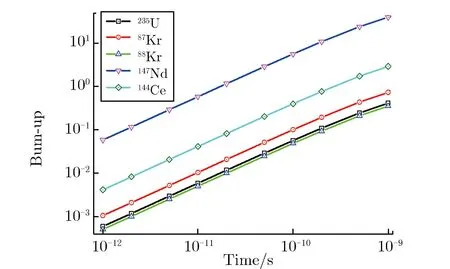
第2节并未针对具体核素采用评价的核数据来做定量分析,下面用燃耗计算程序针对重要裂变产物进行计算分析。CINDER90是一款典型的裂变燃耗计算程序,利用自带的核数据库可计算出中子辐照下材料中的核素总量[4]。设热中子注量率分别为1×1014cm-2·s-1和1×1030cm-2·s-1,在保持中子注量率不变的条件下,铀材料中两种中子注量率下235U和部分裂变产物的核子数密度随时间的变化关系如图3所示。由图3可见,低中子注量率条件下,235U的核子数密度要经过很长的时间才会显著减小,裂变产物87Kr,88Kr,147Nd,144Ce的核子数密度先增大,随后进入平衡状态,最后随235U核子数密度的下降而降低;高中子注量率条件下,裂变产物随中子作用时间延长成线性增长,随着235U核子数密度的下降而下降。这与前面的定性分析完全一致。
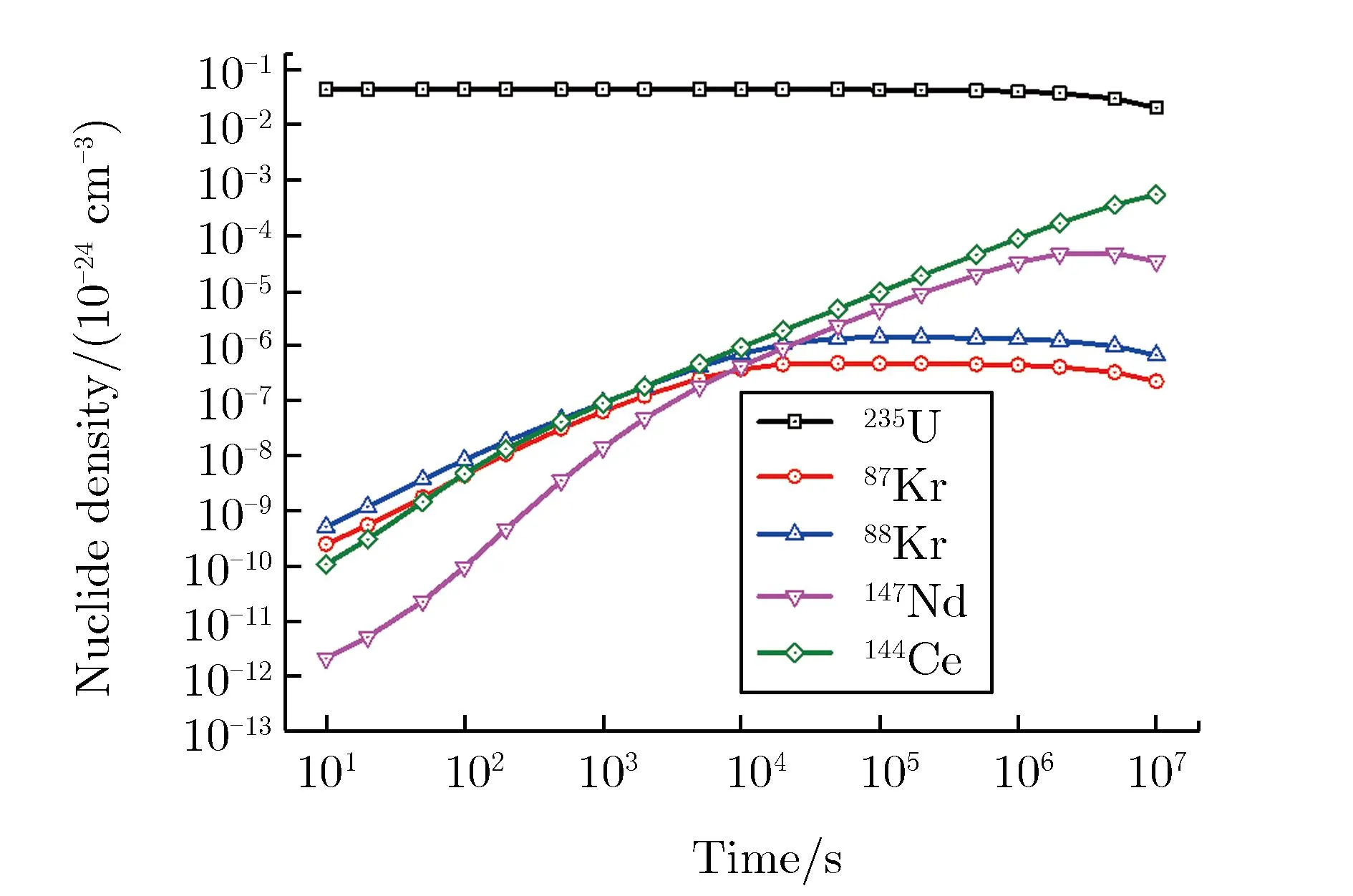
(a)φ=1×1014 cm-2·s-1
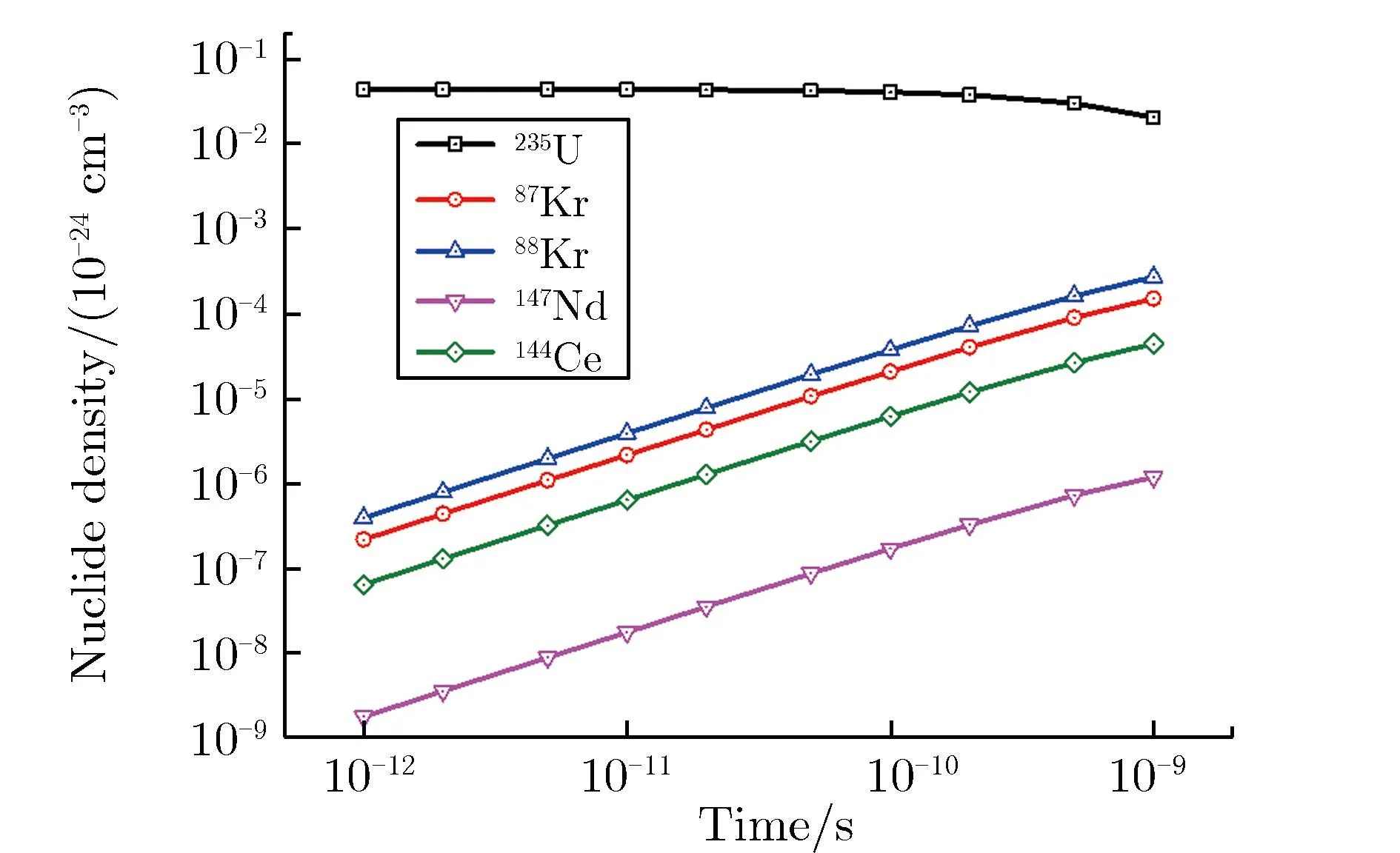
(b)φ=1×1030 cm-2·s-1
根据235U核子数密度变化情况可知CINDER90的计算中235U的消失截面为 766 b。235U的裂变截面取656 b,根据不同时刻235U的核子数密度与初始密度的差即可得到用235U的消失量计算的裂变燃耗。利用裂变产物的核子数密度除以相应的产额再除以235U的初始核子数密度,即可得到用裂变产物生成量计算的235U裂变燃耗。低中子注量率条件下由于中子作用的时间很长,裂变产额采用累积产额;高中子注量率条件下则由于中子作用时间很短,裂变产额采用独立产额,计算中采用的裂变产物核数据如表2所列。

表2 计算中采用的裂变产物核数据
利用CINDER90程序计算得到两种中子注量率下不同方法计算的235U裂变燃耗,如图4所示。由图4可见,低中子注量率条件下计算的裂变燃耗与图1的结果类似,高中子注量率条件下的计算结果与图2中裂变产物表观消失截面的最小结果类似,这说明各裂变产物的表观消失截面不大,比235U小很多。各裂变产物计算的裂变燃耗有差异,主要是由于其独立产额不准确。

(a)φ=1×1014 cm-2·s-1
(b)φ=1×1030 cm-2·s-1
由高注量率下的计算结果可知裂变产物的消失截面很小,故高中子注量率下实验产额的修正较小。低中子注量率下,忽略裂变产物的消失截面,按照两种方法计算的裂变燃耗应该一致的原则,引入与中子作用时间相关的实验裂变产额,表示为
(14)
利用式(14)计算各裂变产物的实验产额随时间的变化关系,根据裂变产物数量,计算得到的裂变燃耗随时间的变化关系如图5所示。由图5可见,当裂变燃耗较高时,根据不同裂变产物数量计算给出的裂变燃耗较一致;裂变燃耗较低时,不同裂变产物的差异则主要来自其独立产额占累积产额的份额及前驱母体半衰期的差异。
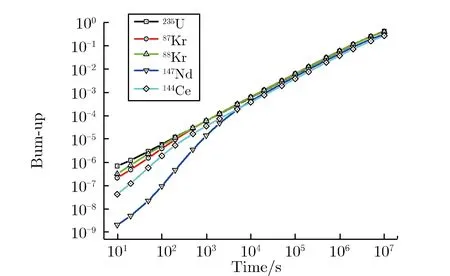
图5 根据裂变产物数量,计算得到的裂变燃耗随时间的变化关系
4 结论
本文针对裂变燃耗计算中低中子注量率条件下实验测量和评价的裂变产额能否应用于高中子注量率条件下裂变燃耗的计算问题,开展了定性分析和数值模拟计算。结果表明,裂变燃耗是影响数据适用性的重要因素。在低燃耗下,用中子作用结束时刻裂变产物的产生量和评价的裂变产额计算的裂变燃耗,与采用裂变核的消失量计算的裂变燃耗一致,且燃耗越高差异越大,但产生差异的原因有所不同:低中子注量率条件下,主要原因是短寿命裂变产物的生成量达到了饱和;高中子注量率条件下,主要原因是裂变产物通过中子核反应有一定量的“消失”。裂变产物相对于裂变核的消失截面越大,高燃耗下两种方法计算的燃耗偏差越大。根据CINDER90计算的结果,裂变产物的消失截面比裂变核的消失截面小很多,高燃耗下两种方法计算的燃耗偏差不大。
因此,实验室条件下测定的裂变产额及其评价结果适用于高中子注量率条件下裂变燃耗的计算,但当裂变燃耗较高时,须仔细评估裂变产物和裂变核消失截面的相对大小。
