舵机减速机构动力学仿真与振动特性研究*

马 景，李 明，班 伟，张鸿涛，纪春佳

（1.中北大学机电工程学院，太原 030051；2.中国船舶集团有限公司，北京 100097；3.宜昌测试技术研究所，湖北 宜昌 443003；4.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161000）

0 引言

鱼雷在运输和水下航行时，外部环境复杂多变，极易受到外界环境的激励作用，鱼雷航速、海况变化等外界激励的频率与舵机系统固有振动频率相近或相同时，会引起共振，表现为大幅度的振动。剧烈的振动会使结构件疲劳或断裂，影响鱼雷舵机减速机构传动的稳定性，造成舵片无法按照控制器指令偏转或偏转位置不准确，无法精确命中目标，贻误战机，导致任务失败［1-2］。

随着航空航天技术、机器人技术等高新技术的发展，行星齿轮传动呈现更广阔的发展趋势。行星齿轮减速器与普通定轴齿轮传动的减速器相比，体积和质量更小，结构更加紧凑，传递功率大，在配齿、结构布局合理的情况下，可实现较大的传动比和传动效率，广泛应用于伺服电动机、步进电动机、直流电动机等传动系统中。蜗轮蜗杆减速器可传递不在同一轴平面上的运动和动力；本身机构零件数少，可节省更大的空间，加上其传动稳定，自锁性好的优点，非常适合用于较大功率的电动舵机减速器。舵机所处的环境状况复杂，为了保证其传动的稳定，有必要对减速机构的振动特性进行分析［3-4］。

模态分析用来确定鱼雷舵机减速机构的固有频率和振型，通过分析共振频率所对应的振型图，可以推断结构的变形趋势，从而对薄弱的地方进行预防与加强。随机振动分析主要研究结构在随机载荷作用下的响应，是一种基于概率统计的谱分析技术［5-9］。本文采用Adams 建立动力学模型，对减速传动机构进行动力学仿真。采用Ansys Workbench 进行振动特性分析。通过模态分析提取减速机构的固有频率和振型，然后施加PSD 载荷谱，对其输出的变形与应力云图进行分析，从而检验减速装置的抗振结构强度，为舵机减速机构的结构和性能优化提供依据［10-12］。

1 舵机减速传动机构动力学仿真

1.1 三维模型建立

舵机减速机构采用三级行星齿轮和蜗轮蜗杆传动，整个舵机系统中，电机输入轴与第一级太阳轮连接，通过三级行星齿轮进行减速，获得大的转矩。传动部分为蜗杆蜗轮，蜗轮蜗杆传动同时起到换向作用，通过蜗轮旋转带动舵片偏转，从而输出所需要的位置信息。基本参数如表1、表2 所示，简化模型如图1 所示。

图1 减速传动机构简化模型Fig.1 Simplified model of reducing transmission mechanism

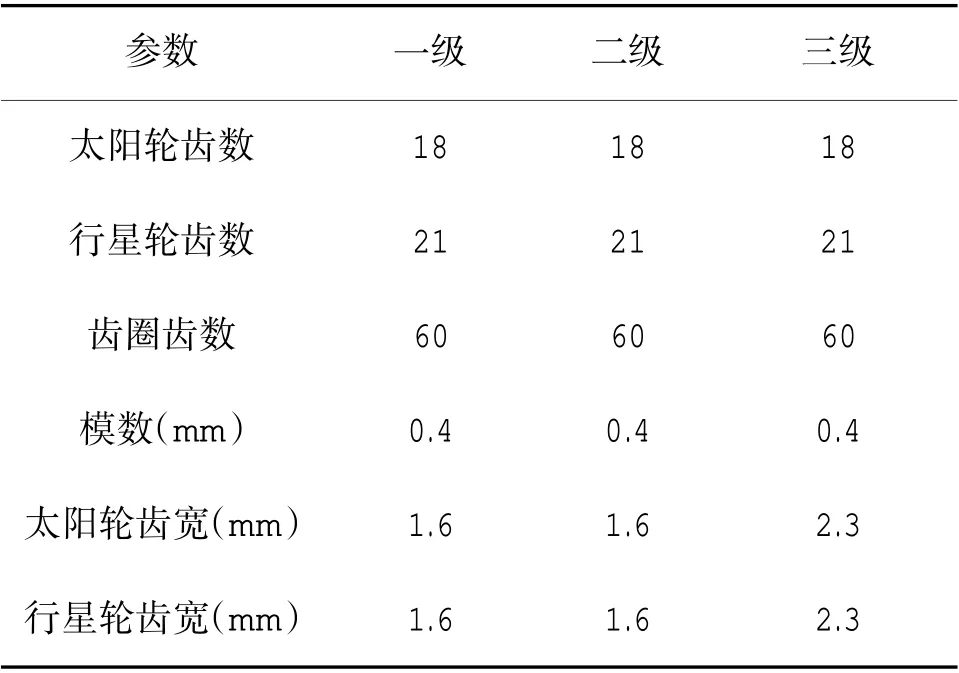
表1 行星齿轮传动基本参数Table 1 Basic parameters of planetary gear transmission

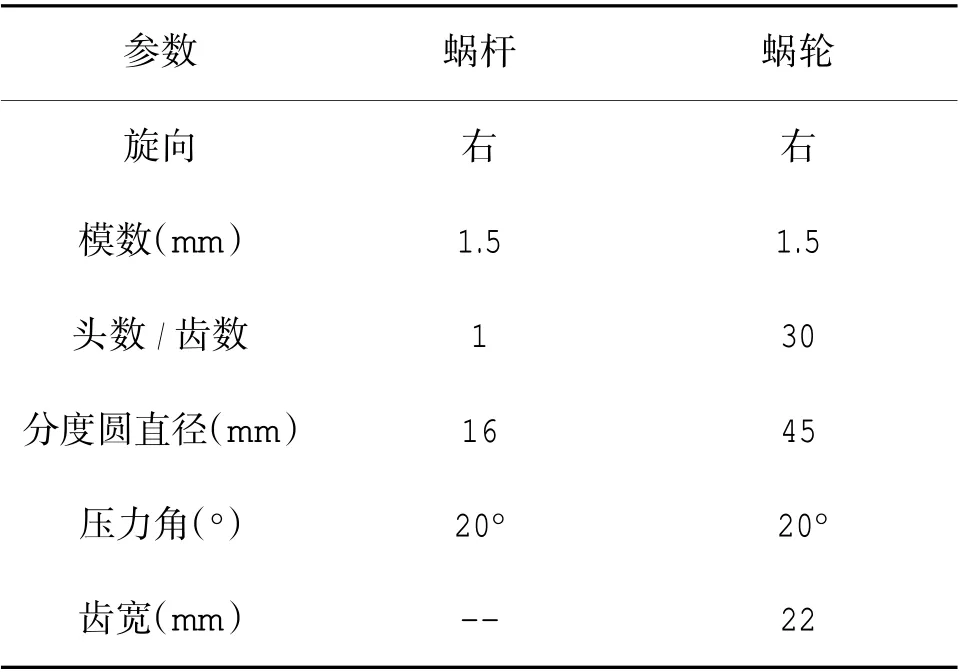
表2 蜗轮蜗杆传动基本参数Table 2 Basic parameters of worm and worm gear drive

1.2 动力学仿真与模型验证

将舵机减速机构三维模型导入Adams2019，赋予材料属性，各结构件材料参数如下页表3 所示。对三级行星齿轮、蜗轮蜗杆机构添加相应的运动副，并将齿圈固定。

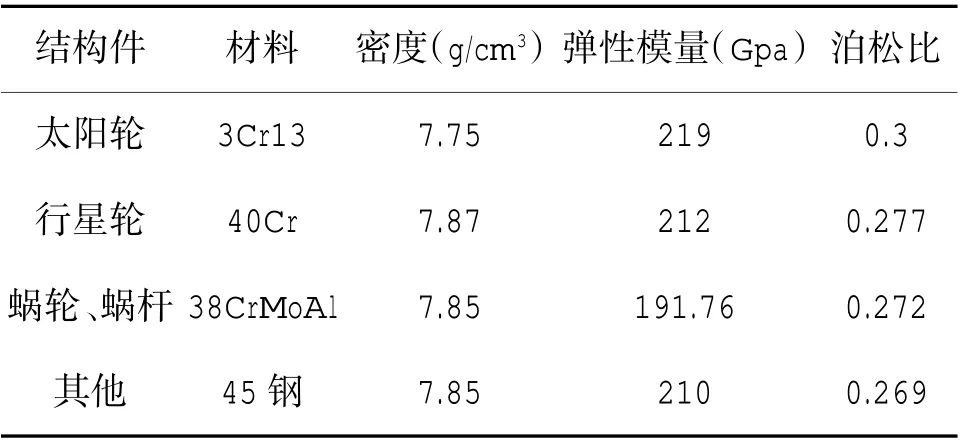
表3 各结构件材料参数Table 3 Material parameters of each structural component

与第一级太阳轮连接的电机轴作为鱼雷舵机减速机构的输入端，对输入端施加9 000°/s（1 500 r/min）的恒定转速，设置仿真时间为1 s，步长500，输入端电机轴角速度曲线如下页图2 所示，输出端蜗轮的角度位移曲线如图3 所示。

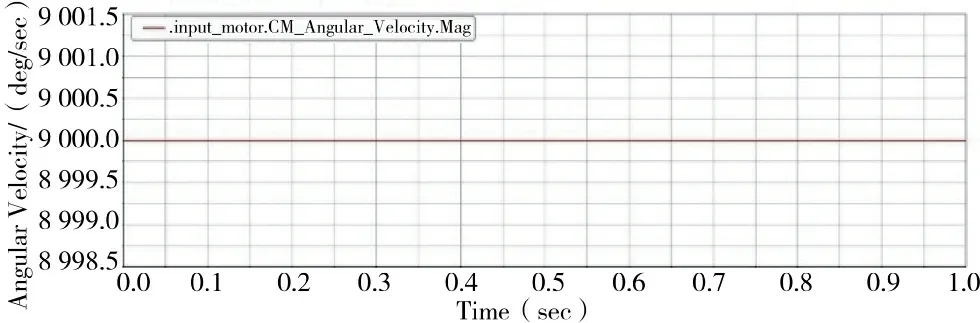
图2 输入端电机轴角速度图Fig.2 Angular velocity diagram of the motor shaft at the input end

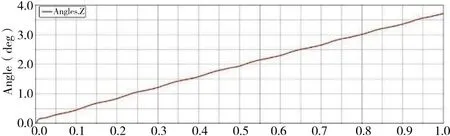
图3 输出端蜗轮角度位移曲线图Fig.3 Angular displacement curve of the output worm gear

舵机减速传动机构理论总传动比为2 441，计算可得蜗轮的输出转速为3.687°/s（0.615 r/min）。图4 为输出端转速理论值与仿真结果对比，为了验证模型的正确性，一般相对误差需控制在5%以内。图中，转速稳定后仿真值与理论值的最大相对误差为4.1%，说明仿真值与理论值基本吻合，由此可得出减速机构模型建立正确。

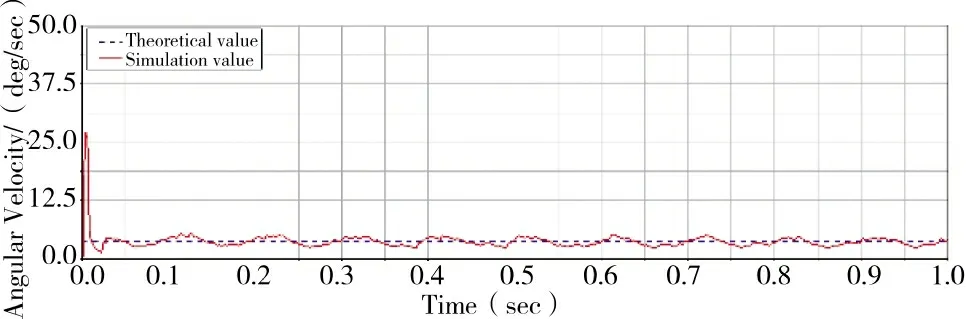
图4 输出转速理论与仿真结果对比图Fig.4 Comparison of output rotation speed theory and simulation results

2 舵机减速机构振动特性有限元分析

2.1 模态分析

模态分析的研究对象为结构的固有频率和振型，也是研究结构振动、噪声、故障诊断等动态响应的基础，广泛用于航空、运输、武器发射等领域。

通常N 维多自由度有阻尼系统的动力学方程为：

从而求解计算ωi，带入式（4）可得固有频率对应的振型φi。

由于模态分析与外界载荷无关，故采用无阻尼系统进行分析计算。

在对鱼雷舵机减速装置有限元分析前，需要对其定义材料属性，此处行星齿轮材料为40 Cr，太阳轮材料为3Cr13，蜗轮蜗杆材料为38 CrMoAl，其他为45 钢，网格划分采用四面体网格方式，如图5 所示。和太阳轮保留其切向自由度，齿圈外表面施加固定约束（Fix support）。蜗杆轴与蜗轮轴颈施加圆柱面约束，切线方向设置为自由。

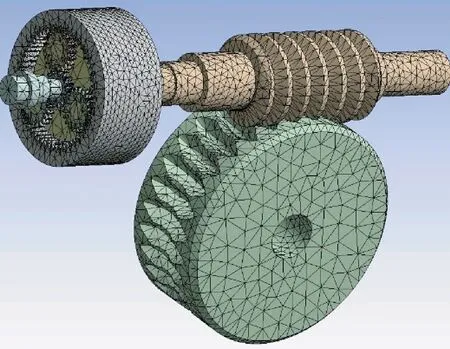
图5 网格划分图Fig.5 Grid division diagram根据鱼雷舵机减速装置的运动特征，行星齿轮

通过仿真分析，前6 阶的模态振型云图如图6所示，鱼雷舵机减速机构振型如表4 所示。

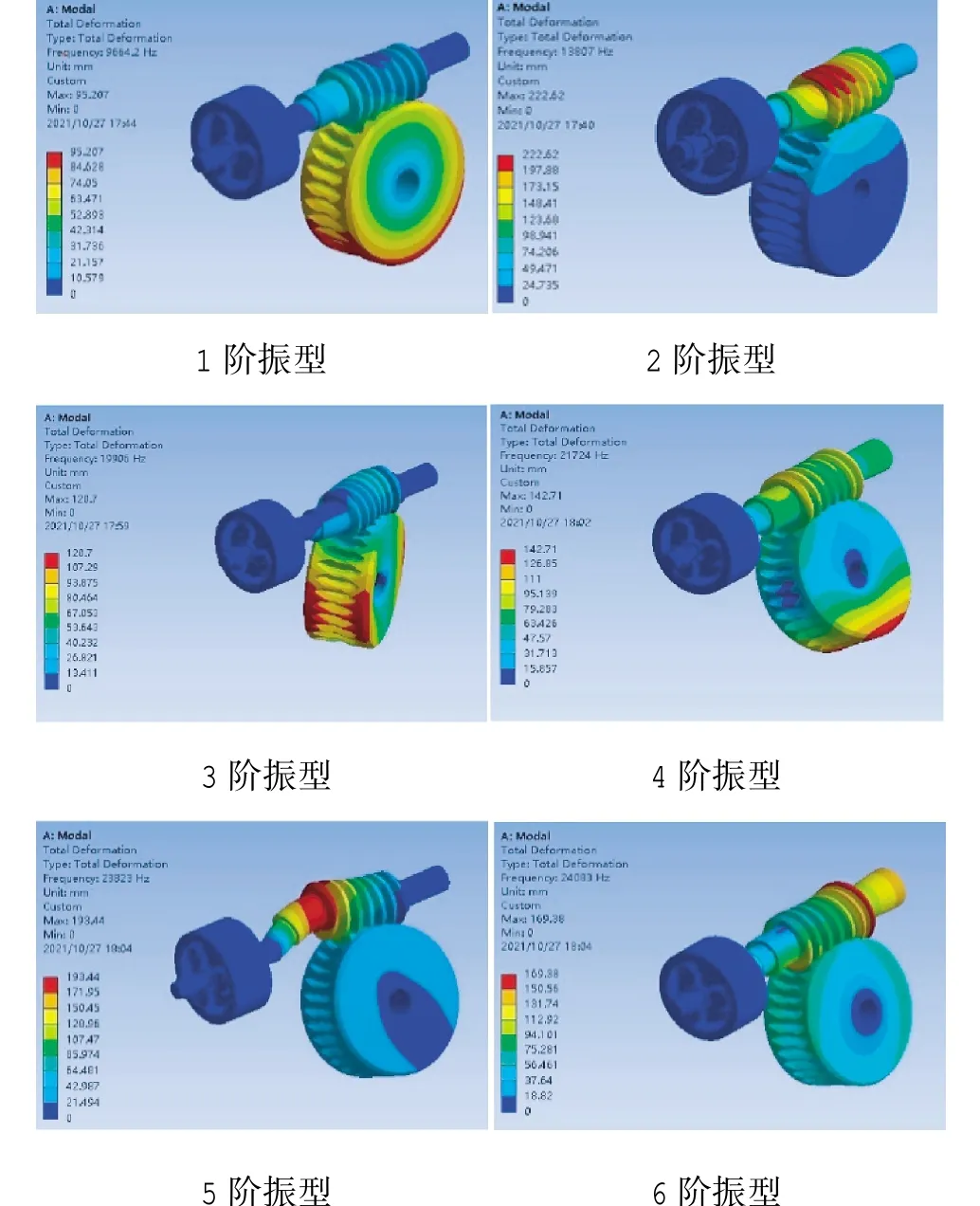
图6 前6 阶的模态振型云图Fig.6 Cloud map of the first six phases of vibration modes

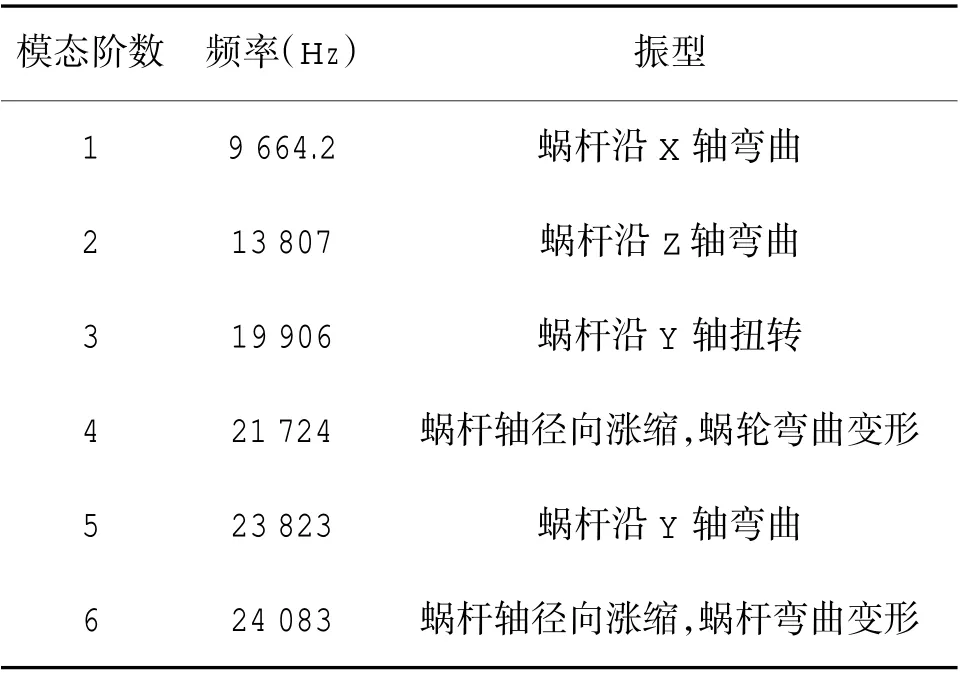
表4 鱼雷舵机减速机构振型表Table 4 Vibration mode table of torpedo steering gear reducing mechanism

从振型形状可判断出在某个共振频率下结构的变形趋势，一阶固有频率越低，表明整体结构的刚度越低，频率越高表示结构的刚度越高。通过以上分析可得，最低频率对应的振型为蜗杆弯曲，说明此方向上的刚度相对较低，需要首先加强。发生共振时，舵机减速机构最主要的振型为蜗杆弯曲，通过对舵机减速装置整体模态分析，可以找出减速装置的薄弱环节，使其固有频率避开振源的激励频率，有利于对结构进行优化和改进，防止共振的发生。

2.2 随机振动分析

鱼雷发射及在水下航行时，外部环境复杂多变，鱼雷航速、海况变化以及螺旋桨、发动机共振会引起随机振动，致使机构可能发生强度及疲劳失效问题，影响传动机构的寿命和稳定性。

模态分析是随机振动分析的基础，在随机振动分析中，输入为随机载荷的功率谱密度函数，即PSD谱，作用在所有约束的位置。输出为PSD 谱的响应，分析对象的变形，应力等。

根据鱼雷在助飞、挂飞等运输过程中所经历的实际振动条件，所施加的加速度功率谱密度如表5所示。

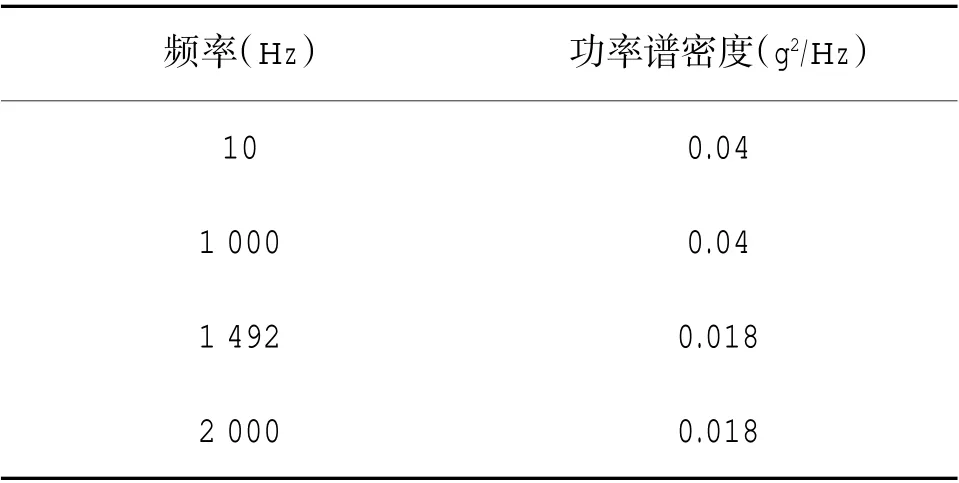
表5 加速度功率谱密度值Table 5 Values of acceleration power spectral density

在Workbench 的Random Vibration（随机振动）模块中，对模型分别添加X、Y、Z 轴3 个方向的PSD谱，PSD Base Excitation（基础激励响应分析）选择PSD G Accelerstion 命令，在Load Date 中输入表5 中数据，其功率谱密度曲线如图7 所示。

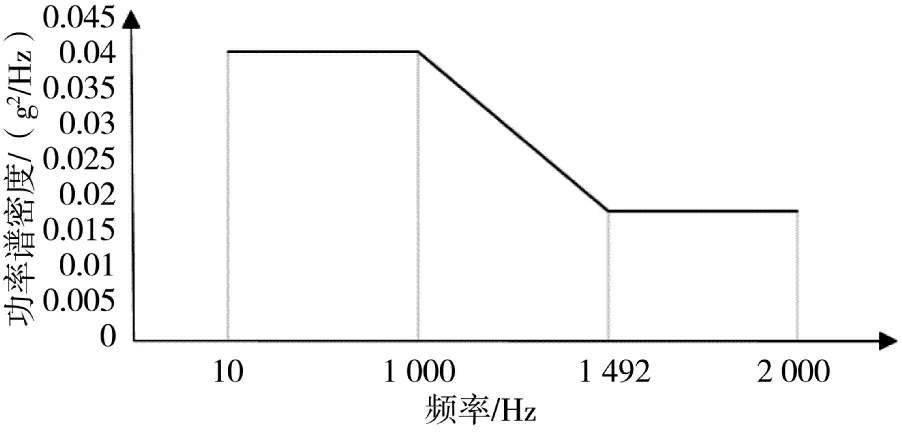
图7 功率谱密度曲线Fig.7 Power spectral density curve

加载随机载荷后，为了更加真实地反映随机振动对舵机减速机构的影响，在Scale Factor 中标准差设置为3σ，表示结构响应有99.73%的概率不超过显示的幅值。

随机振动后处理得出的整体机构3σ 位移、应力如图8 所示，通过云图可以看出，最大变形位移在Y 方向上，为8.94×10-8mm，发生在电机输入轴上；最大应力也在Y 方向上，为1.404 4×10-3Mpa，发生在太阳轮轮齿上。从而说明在电机输入轴和太阳轮轮齿位置处产生的振动能量较大，是结构薄弱的地方，可以为结构优化提供参考。

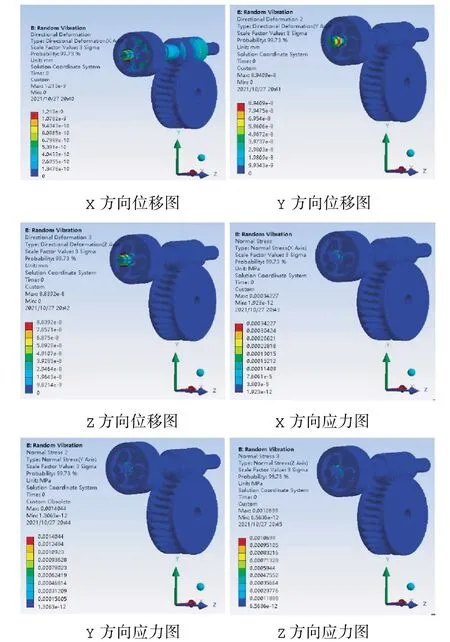
图8 整体减速机构位移、应力云图Fig.8 Displacement and stress nephogram of the overall deceleration mechanism

在X，Y，Z 3 个方向加载随机振动激励条件下，通过应力应变云图分析得到的各部件3σ 应力、应变结果如表6 所示。

2.3 结果分析与强度校核

通过对下页表6 的分析，对于行星齿轮系，随机振动条件下X、Y、Z 3 个方向上最大应力值为1.404 4×10-3Mpa，发生在一级太阳轮齿处，3Cr13的许用应力为360 Mpa。取安全系数为1.5，根据安全裕度的计算式得，Ms＆gt;0，因此，结构满足强度要求。对于蜗轮蜗杆，随机振动条件下X、Y、Z 3 个方向上最大应力值为3.681 5×10-5Mpa，发生在蜗杆轮齿处，38CrMoA1 的许用应力为557 Mpa，Ms＆gt;0，说明舵机减速传动机构在随机载荷激励下满足强度要求，有较高的可靠性。

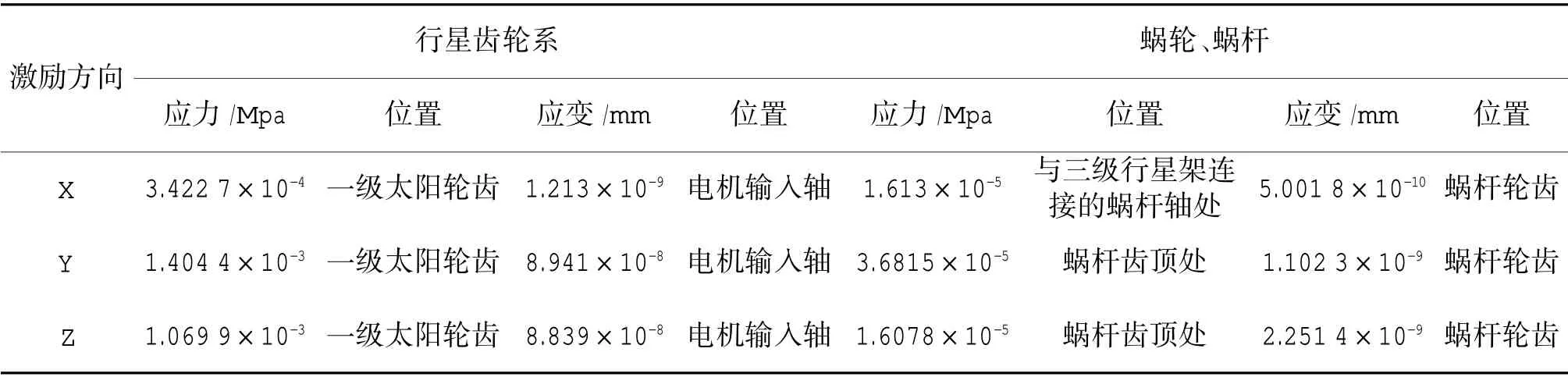
表6 各向随机振动条件下3σ 最大应力和应变对比表Table 6 Comparison table of 3σ maximum stress and strain under anisotropic random vibration

3 结论

1）本文以鱼雷舵机减速传动机构为对象，结合外界所处的激励环境，通过有限元方法进行了振动特性分析。模态分析判断机构在不同频率下振型，在结构设计时使固有频率与周围激励频率分离，避免共振的发生。通过随机振动的仿真分析，得出结构应力、变形情况，电机输入轴和一级太阳轮轮齿以及蜗杆与蜗轮啮合处所受振动量级较大，需要在设计时重点关注。

2）通过有限元分析法对舵机减速机构振动特性的分析，对机构进行优化或增加约束，一定程度上可避免或减少外界激振源对机构造成的大幅振动，有利于舵机减速机构工作条件的改善和使用寿命的提高，此分析方法也可为舵机其他结构部件的分析提供参考。