例谈圆锥曲线中非对称问题的处理策略

金保源

华南师范大学附属惠阳学校 (516200)

在圆锥曲线问题中，将直线方程与曲线方程联立后，消去x或y，得到方程再结合韦达定理来进行其它运算是常见的解题思路，但是在某些问题中可能会涉及需要计算两根系数不相同的代数式.像这种“非对称”的韦达定理结构，通常是无法根据韦达定理直接求出的，大部分学生遇到这样的问题束手无策.本文以一道高三调研试题为例，提出了非对称韦达问题常见的六种解决思路，供读者参考.

1 试题呈现

(1)求椭圆C的标准方程；

(2)若椭圆C的左、右顶点分别为A、B，点M、N是椭圆上异于A、B的不同两点,直线BN的斜率为k(k≠0)，直线AM的斜率为3k，求证：直线MN过定点.

2 解法探究

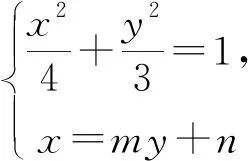
思路1 恒等变形，化单变量

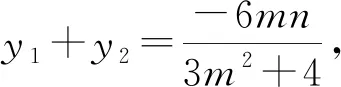
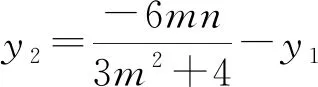
思路2 积化为和，降次处理

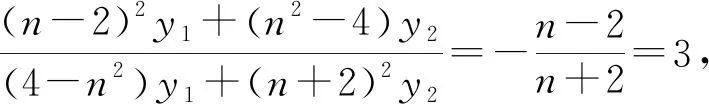
思路3 代入曲线，平方消元

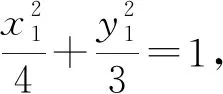
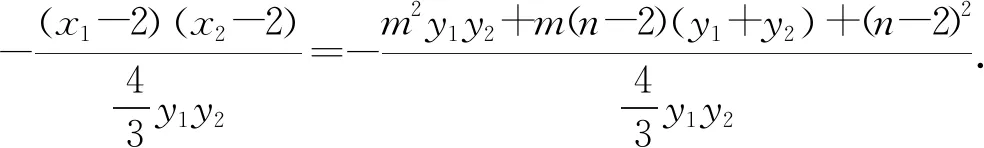
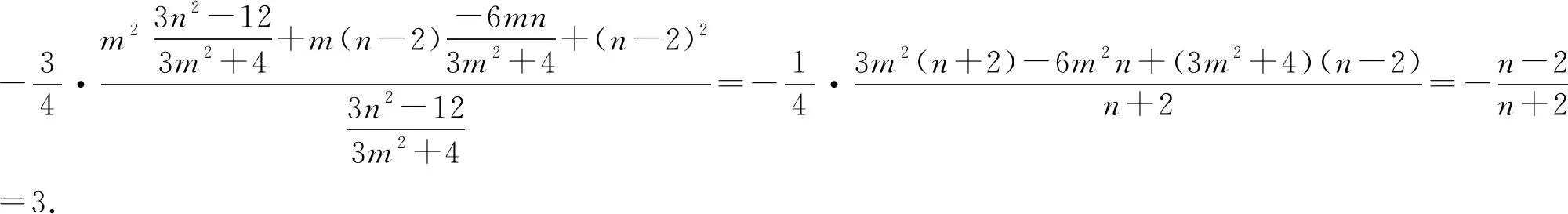
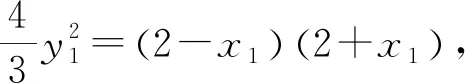
思路4 待定系数，和差转化

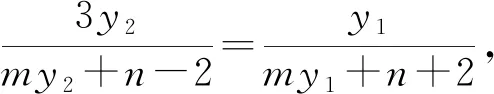
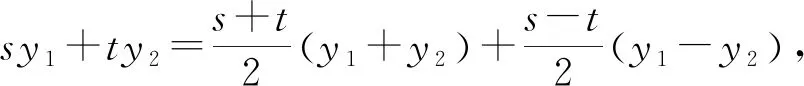
思路5 式子分离，配凑乘积

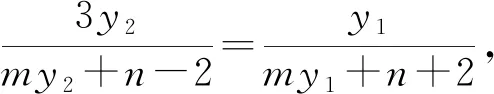
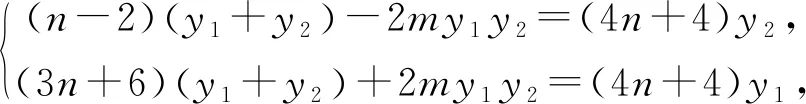
点评：对于非对称结构sy1+ty2+my1y2=0，可以将式子配凑成和积形式的对称式，即

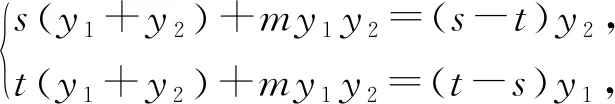
思路6 第三定义，构造对偶

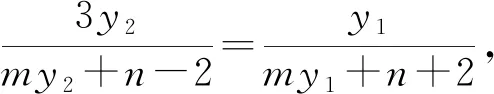
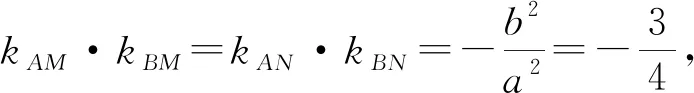
3 小结启示

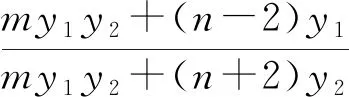
解决问题时,只有我们真正把握住问题的本质,才能真正的理解问题进而解决问题.“不对称”凭借线性运算、作商、乘方等可变为能够“直接”应用韦达的“对称”情况，这是本文解法的思想根源.一般地，高中解几试题中的所谓“不对称”其实也属于“对称”，这是由二次曲线本身所决定的，其不对称仅仅是代数形式上“不直接”.在教学中,教师只有从更深的角度揭露本质,才能真正让学生在数学学习中得到乐趣,开拓学生眼界,开阔学生思维,培育学生优秀的个性,真正达到培养学生数学核心素养的目的.