从2021年一道高考题谈圆锥曲线上四点共圆问题

李 婧 卢荣亮

江苏省南京市燕子矶中学 (210038)

本文从2021年一道高考题谈起，用从特殊到一般的方法探究圆中的相交弦定理、割线定理以及切割线定理在圆锥曲线中的表现形式，进而发现圆锥曲线上四点共圆的一个更为一般的充要条件[3][4].

1. 原题赏析

(1)求C的方程；

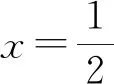
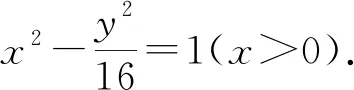
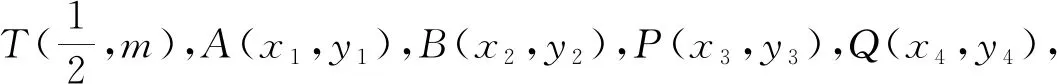
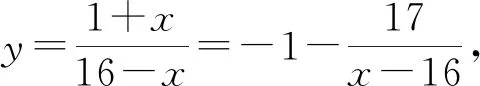
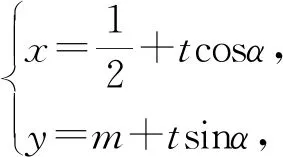
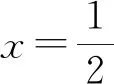
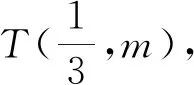
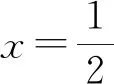
2.类比推广

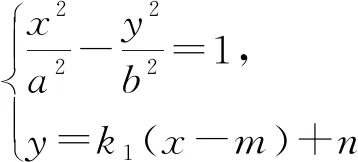
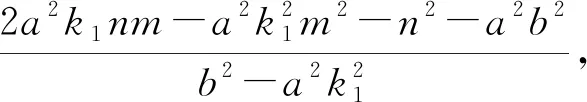
问3：这个结论的逆命题成立吗？

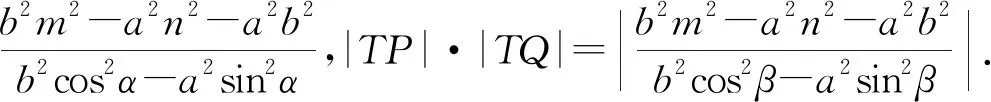
问4：如果把双曲线换成椭圆，上述结论还成立吗？

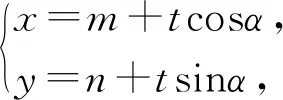
问5：如果把椭圆换成抛物线，这个结论依然成立吗？

推广4 已知抛物线C的方程为y2=2px(p>0)，设点T(m,n)(m,n∈R)，且点T不在抛物线上，过点T的两条直线分别交C于A，B两点和P，Q两点，若这两条直线的斜率都存在，分别设为k1和k2，则k1+k2=0的充要条件是|TP|·|TQ|=|TA|·|TB|.

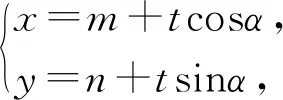
3.追根溯源

在研究这个问题的过程中，笔者进一步发现圆锥曲线中的这些结论实际上就是圆中的相交弦定理和切割线定理的推广，只不过此时需加两直线斜率之和为的条件.

(1)圆中的两条弦相交，且交点在圆内部，即得到相交弦定理：圆O的两弦AB，CD交于圆内一点M，则|MA|·|MB|=|MC|·|MD|.

(2)圆中两条弦所在直线相交，且交点在圆外部，即得到割线定理：过圆O外一点M作圆的两条割线AB，CD与圆相交于A,B,C,D则|MA|·|MB|=|MC|·|MD|.

注：相交弦定理的逆定理和割线定理的逆定理依然成立，即两直线AB，CD交于一点M，且|MA|·|MA|=|MC|·|MD|，则A，B，C，D四点共圆.

(3)在推广3和推广4中，若点T在圆锥曲线内部，即是圆锥曲线的相交弦定理；若点T在圆锥曲线外部，即是圆锥曲线的割线定理.

切割线定理 过圆O外一点M作圆的一条割线交圆于A，B点，作圆的一条切线MT，与圆切于点T，则|MA|·|MB|=|MT|2.

圆中的切割线定理可以进一步推广到圆锥曲线中吗？

4.再推广

推广5 已知点T在圆锥曲线C外，过点T的直线l与圆锥曲线交于C，B两点，过点T的直线m与圆锥曲线切于点D，若这两条直线的斜率都存在，分别设为k1和k2，则k1+k2=0的充要条件是|TA|·|TB|=|TD|2.

推广6 已知点T在圆锥曲线C外，过点T的直线l与圆锥曲线C切于点A，过点T的直线m与圆锥曲线C切于点B，若这两条直线的斜率都存在，分别设为k1和k2，则k1+k2=0的充要条件是|TA|=|TB|.

以上推广1-4，实际上我们可以用一个定理表述，即

定理若四个不同的点A，B，C，D在圆锥曲线(标准方程)上，则四点共圆的充要条件是存在两条分别经过其中两点的相交直线的倾斜角互补.

注：因为从圆锥曲线(标准方程)上四个不同的点中任意选取两点，一共可以构成六条不同的直线，则必存在两条斜率都存在的相交直线，所以此定理的证明由本文中的“推广1-4”易得.

点评：该定理是文献[3]中定理更为一般的形式，它有一个妙处：我们可以基于此，把四点共圆这一条件隐藏起来，即用数学的符号语言去表达它，编制不同的试题让学生解决；除了本文中的相交弦定理的逆定理和割线定理的逆定理可以刻画四点共圆，还可以用西姆松线定理的逆定理[2]与托勒密定理的逆定理[2]等来刻画四点共圆.

问题：我们知道圆的切割线定理以及它们的逆定理都是用纯几何法证明，那本文中圆锥曲线的切割线定理能否用纯几何法证明呢？

笔者至今没有解决这个问题，希望读者朋友能给予指导.

结语：经笔者查阅文献，发现本文中的定理与文献[4]和文献[5]类似，有些遗憾，但是笔者的想法和他们又有些不同；因此，笔者把从发现这个问题、分析这个问题到解决这个问题，进而提出新问题的心路历程完整地展现给大家，供相互学习、共同进步.