复杂环境下的无人机三维路径规划

林思伟，席万强，李青云，林俊志，李 鹏,

(1.南京信息工程大学，南京 210000； 2.无锡学院，江苏 无锡 214000)

0 引言

无人机(UAV)作为移动机器人的研究热点，不局限于地面的工作空间，使得其拥有更广阔的应用场景，从高空作业到低空与地面移动机器人进行相互协作，甚至于控制小型无人机在室内进行作业。随着海拔的降低，随之而来的是周围环境复杂性的提高[1]，路径规划的难度也相应提高，如何设计出一条符合UAV运动约束的较短距离的安全路线成为了研究热点[2]。

无人机路径规划算法包括图搜索法、智能仿真算法、采样法和基于人工智能算法等[3]。文献[4]实现了lazy_Theta*算法在三维路径规划中的应用，并且以分段变阶贝塞尔曲线进行路径优化；文献[5]将智能算法用于路径规划，由改进的遗传算法生成路径点，再由三次B样条曲线进行平滑；文献[6]针对三维路径设计，将原A*算法的邻近节点扩展的方式改成采用球形节点扩展的方式，实现了三维空间的搜索，从而实现路径规划。但是上述算法都是针对地图环境已知的情况进行的全局静态路径规划，对于未事先检测到的障碍物信息则无法进行避障。针对此，文献[7]采用人工势场算法，并利用碰撞锥进行改进，对于易陷入局部最优的问题，则通过设计模糊控制以调节系数的方式进行解决；文献[8]将避障问题描述为部分可观察马尔可夫决策过程，并采用动态规划方法求解近似最优状态-动作组合。

上述进行UAV全局静态路径规划的研究中，皆是考虑在能够实现静态避障的情况下，如何得到较短距离的解，然后采用将路径进行曲线优化的方式使之具有C1，C2连续性，使得规划路径在速度及加速度上不会发生突变，利于后面进行UAV轨迹跟踪时的控制。但进行规划时并未考虑到UAV的运动约束，仅是保证了其路径的C1，C2连续性，并不能保证UAV可以正常顺利地进行轨迹跟踪而不会发生侧翻，后面的UAV动态避障研究中多数也没有考虑此问题。文献[8]通过进行动作组合的设计避免了这种情况的发生，动作组合在保证了控制稳定性的优势下，也约束了更多运动模式的可能性。

针对上述研究的不足，本文通过结合静态规划和动态规划，融合Theta*算法与改进DWA(Dynamic Window Approach)算法，实现静态上能够有较短的路径，动态上能够对未知障碍物信息避障，并在DWA算法的运动约束中加入UAV的动力学模型，使得最终生成的路径符合UAV的飞行性能，最终输出结果可以得到UAV各电机的转速变化以及UAV各状态量的变化。

1 三维地图建立

为了应用和验证提出的算法，本文创建了一个表示已知复杂环境的80×80×20的节点网格表示无人机周围环境信息。如图1(a)所示，网格中填充了代表室内空间的物体或城市建筑的障碍物。障碍物的位置和大小被随机分配，它们的长宽被设定在3×3和5×5大小之间。数据结构是一个简单的80×80矩阵，元素的离散值为0～20。与数字高程模型(Digital Elevation Model，DEM)[9]类似使用数值表示各元素的地面标高。图1右侧的颜色栏表示颜色所对应的海拔高度。

图1 标准网格和带缓冲区网格Fig.1 Standard grid and buffered grid

考虑UAV本身具有一定的空间大小，为增加路径的安全性，在障碍物周围创建一个缓冲区。如图1(b)所示，将障碍物高度值分配给它周围的节点，同时将障碍物和周围节点的高度值都提高1，以此在标准网格的基础上构建出带缓冲区网格，在其上进行路径规划，增大其安全性。

2 Theta*算法

Theta*算法是一种广度搜索算法与贪婪算法的融合算法，从起始节点开始，将起始节点的邻近节点加入探索队列[10]，以式(1)进行各个邻近节点的代价评估。称起始节点为这些邻近节点的父节点，这些邻近节点为起始节点的子节点。选取当前列表代价最低的邻近节点，再继续将此节点的邻居节点加入探索队列中。重复此过程直至探索到终点节点。上述也是A*算法的大致原理。其具体算式为

fTheta*=kd*D+kh*H+ke*E

(1)

式中:D是从起始节点移动到节点的成本(移动距离)，每次通过计算当前节点到父节点的欧氏距离加上父节点的D求得;H是从节点到目标点的启发式距离(移动距离);E是通过节点时的交通风险成本(进行避障)，路径点与障碍点重合时置1,无重合则为0;参数kd,kh和ke是经过适当调整的权重系数，用于调整路径特性并使其达到目标点。

相较于A*算法，Theta*算法在每次得到最小代价节点时，通过判断节点与节点之间是否有可见线的方式进行节点父节点的重链接，回溯父节点的D进行当前节点的D更新，实现以任意角度进行规划，而不会像A*算法般受限于仅能进行45°角转向。Theta*算法生成的全局路径规划，仅用返回路径转折点的节点坐标。节点与节点之间通过直线插值法生成连续离散点，构建的路径相较A*算法路径更自然、平滑。相比一些在用A*算法规划后去除冗余节点的改进做法，Theta*算法规划过程中进行父节点的重新链接，更新其移动成本，实现更优更短的路径规划。

图2所示为在40×40×20的三维地图中A*算法与Theta*算法的对比，图2(b)为图2(a)的俯视图。

图2 A*算法与Theta*算法对比

由图2可以看出：Theta*算法规划出来的路径比A*算法规划出来的路径更平滑，转折点更少；尤其是在高度方面，A*算法仅能以一种类似台阶的方式进行高度的爬升与下降。在此空间大小下进行1000次障碍随机生成与路径规划，Theta*算法平均所需时间为A*算法的76.67%,规划路径平均长度为A*算法的92.84%。

3 改进DWA算法与Theta*算法融合

在詹京吴等[11]研究下，针对无人小车实现了在二维平面上A*算法与DWA算法的融合路径规划算法，其选取A*算法生成的部分路径点作为DWA算法跟踪的目标节点。由于A*算法返回的路径节点是连续离散点，其通常做法是：将路径点进行等分，取每等分的最后一个路径点作为DWA算法目标节点，令小车根据DWA算法跟随着A*算法规划出的路径，最终到达终点节点。这导致目标节点选择无特征性，移动机器人易偏移于连续转折的路径上，失去全局路径规划算法的指导作用。而Theta*算法仅返回转折点处路径节点，以转折点作为目标节点具有特征性，移动机器不易过大偏移较优路径。

DWA算法是一种常用于动态避障的算法[12]，其本质是通过采样移动机器人的速度变化范围，将每一个采样速度代入当前移动机器人位置进行模拟预测，返回预测出来的位置及速度信息。通过评价函数

G=α*e+β*dE+γ*v

(2)

求得每次预测位置及速度的得分G，以贪婪算法的思想，每次选择最优解，在每次的最优解下进行下一轮的速度采样模拟预测，直至终点。式(2)中:α，β，γ是权重系数；e为航向角评价值，表示当前前进方向与终点方向角度偏差；dE是与障碍物之间的避障距离得分,即UAV与最近障碍物之间的欧氏距离；v是当前速度得分。其中:

(3)

(4)

式中:Pgoal为当前跟踪的目标节点位置;Pt为预测位置；vx,vy和vz为UAV在三轴上的分速度大小。

计算dE时，通过如图3(a)到图3(b)所示切片的方式，并通过如图3(c)所示随着距离由近及远地旋转扩散搜索障碍物。图3(c)所示为以五角星为中心扩散搜索周围2圈障碍物：每次搜索的4个点，都是由一个点以绕中心每次旋转90°的方式生成，这4点距离中心点的距离都是相同的，从而做到由近及远地搜索。每一圈的搜索点数是(n+1)×4，n代表第几圈。如果以中心建立直角坐标系，就是将第一象限及其x正半轴上的搜索点位，按照距离中心点的距离，从小到大依次以绕中心点每次旋转90°进行旋转扩散式搜索。当碰到障碍物或者达到搜索圈数时，跳出搜索循环。基于障碍物为不浮空矩形，高层障碍物信息总是少于底层障碍物信息，仅搜索水平四周及UAV正下方一层的3×3的搜索空间。

图3 障碍物搜索Fig.3 Obstacle search

图4所示为四旋翼简易结构图。

图4 四旋翼结构示意图Fig.4 Diagram of quadrotor structure

由Newton-Euler方程推导可得四旋翼动力学模型[13](本文变量只考虑数值大小)

(5)

(6)

其中:w1,w2,w3和w4分别表示4个电机的转速;x,y,z分别表示在世界坐标系三轴上的分量;φ,θ和ψ分别表示滚转角、俯仰角和偏航角。

图5 DWA算法流程图Fig.5 Flow chart of DWA algorithm

4 仿真验证与结果分析

为了验证融合算法的有效性，基于Matlab2021a仿真环境，生成如图6所示80×80×20地图模型，其中，高于5的障碍物占地图空间的12.61%，高于10的障碍物占地图空间的6.54%，高于12的障碍物占地图空间的5%。电机范围取0～7000 r/min，采样间隔取100 r/min。采样时间为0.1 s。选取文献[13]中的无人机参数作为仿真参数，如表1所示。起点坐标为(5,7,12),以绿色矩形进行标注;终点坐标为(48,61,8),以红色菱形进行标注。

表1 四旋翼物理参数Table 1 Quadcopter physical parameters

角度及角速度约束如下：-0.785 4 rad≤φ≤0.785 4 rad；-0.785 4 rad≤θ≤0.785 4 rad；-0.349 1 rad/s≤dφ≤0.349 1 rad/s；-0.349 1 rad/s≤dθ≤0.349 1 rad/s；-0.698 1 rad/s≤dψ≤0.698 1 rad/s。其中，dφ,dθ和dψ分别为滚转角速度、俯仰角速度和偏航角速度。

如图6所示，用Theta*算法对原始地图进行全局路径规划。当新增障碍物时，原Theta*算法规划的路径被挡住，Theta*与DWA融合算法仍能绕过新增障碍物，且运动约束生成的路径比Theta*算法规划出来的路径更平滑。

将融合算法生成的路径关于时间求导，求得其三轴速度变化情况，如图7所示。在三轴速度上皆无突变，路径满足C1连续性。在飞行过程中，UAV滚转角φ、俯仰角θ和偏航角ψ的角度变化如图8所示，电机转速变化如图9所示。在16 s附近发现电机转速皆突变为0 r/min，对应位置在图6(d)中用白色五角星标记，恰是飞行拐点，UAV选择以仅受重力的方式，通过惯性调整姿态和飞行航向。然后增大Y轴方向速度降低X轴方向速度，飞向目标点。

图7 三轴速度变化Fig.7 Three-axis speed change

图8 三轴角度变化Fig.8 Three-axis angle change

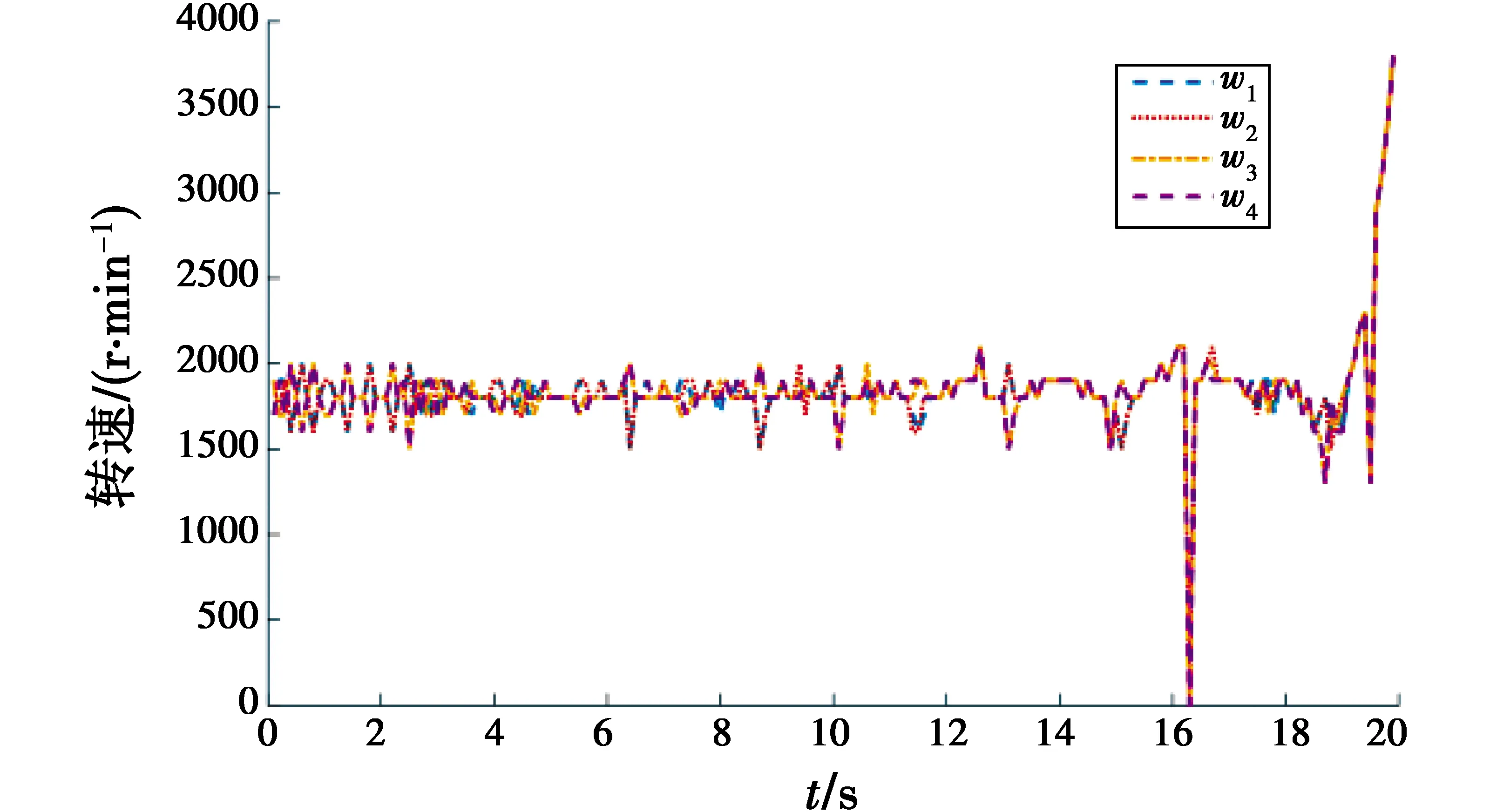
图9 电机转速变化Fig.9 Motor speed change

结合上述信息发现混合算法路径下的飞行速度连续，而Theta*算法的路径转折处是位移对于时间的不可导点,会存在速度突变。并且所提方法规划出的路径，在无干扰的情况下进行轨迹跟踪仅需考虑跟踪4个电机转速，相较于以前需要对位置进行跟踪控制，其将控制对象系统简化到电压输入转速输出这一环节，降低控制器的设计难度。

5 结论

通过研究对比发现,Theta*算法相较于A*算法更易与改进DWA算法进行融合，使得DWA算法的目标节点选取更加明确，大大减小UAV偏离Theta*算法规划出的路径的可能性，更适用于室内或者城市中复杂环境下的运动规划。此外，不需要实时更新地图或保持空间布局不变的使用要求，将使得UAV的应用范围进一步扩大。其中，以控制电机转速进行UAV轨迹跟踪的方式，更适用于室内少干扰的环境，相较于不考虑UAV动力学模型进行路径规划的方式，本文方法生成的路径更利于实际UAV的轨迹跟踪。